I Przestrzeń metryczna. Metryka euklidesowa w Rⁿ. Kula, otoczenie, wnętrze, domknięcie. Zbiory otwarte, domknięte, zwarte i spójne na prostej.

Definicja

Przestrzenią metryczną nazywamy parę
gdzie
oraz
przy czym spełnione są warunki:

1).

2).

3).

Elementy zbioru X nazywamy punktami, funkcję
się metryką na X, zaś wartości
nazywa się odległością w metryce
.

Definicja

Metrykę
daną wzorem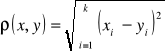
nazywamy metryką euklidesową na R^k, zaś p-ń metryczną
wraz ze strukturą p-ni wektorowej nazywamy k-wymiarową p-nią euklidesową.

W szczególności w R² metryka euklidesowa ma postać

Dla

Definicja

Niech
będzie p-nią metryczną

a). kulą (otwartą) o środku
i promieniu
w p-ni
nazywamy zbiór
, który oznaczamy przez
.

b). otoczeniem punktu
nazywamy każdą kulę o środku w tym punkcie.

Definicja

Niech
. Zbiór P nazywamy przedziałem jeśli

Przykład

,
,
- zbiory otwarte na prostej

Definicja

Niech
.

a). mówimy, że
jest punktem wewnętrznym zbioru A, gdy istnieje liczba r>0 taka, że
. Zbiór punktów wewnętrznych zbioru A nazywamy wnętrzem zbioru A i oznaczamy przez IntA.

b). domknięciem zbioru A nazywamy zbiór

c). mówimy, że zbiór A jest otwarty, gdy każdy punkt A jest jego punktem wewnętrznym (inaczej gdy
).

d). mówimy, że A jest domknięty gdy
jest otwarty.

Definicja

Mówimy, że podzbiór A p-ni metrycznej X jest zwarty, gdy podp-ń metryczna A jest zwarta tj. gdy ciąg punktów zbioru A zawiera podciąg zbieżny do pewnego punktu zbioru A.

Definicja

Mówimy, że podzbiór A p-ni metrycznej X jest spójny, gdy podp-ń metryczna A jest spójna tzn. gdy A nie da się przedstawić w postaci sumy dwóch zbiorów niepustych, rozłącznych i otwartych w A.

Twierdzenie

Niech
będzie dowolną p-nią metryczną. Każdy podzbiór zwarty tej p-ni jest domknięty i ograniczony.

Przykład

Dowolny przedział
jest zwarty na prostej.

Przedział
nie jest zbiorem zwartym, bo nie jest zbiorem domkniętym .

Przedział
nie jest zbiorem zwartym, bo nie jest zbiorem ograniczonym.

Twierdzenie

Podzbiór p-ni
jest spójny
gdy jest on przedziałem.

Uwaga

Metrykę definiujemy na dowolnym zbiorze a normę na p-ni liniowej.

---