
Matematyka – wykład 1
Macierze i wyznaczniki
dr Ewa Wędrowska

23.05.21
2
Literatura:
1. „Analiza matematyczna w zadaniach”, tom I,
Krysicki, Włodarski
2. „Matematyka wspomagająca zarządzanie”
pod redakcją Krzysztofa Piaseckiego
3. „Matematyka w zadaniach”, Piszczała,
Piszczała, Wojcieszyn

23.05.21
3
Podstawowe definicje
Macierzą liczbową o n wierszach i m
kolumnach
nazywamy prostokątną tablicę
zawierającą m·n liczb. Tablicę taką
zapisujemy w postaciach następujących:
Jeśli elementy macierzy są liczbami rzeczywistymi to
macierz nazywamy
rzeczywistą
. Macierz może
zawierać inne elementy, np. funkcje; macierz taką
nazywamy
funkcyjną
.
nxm
...
...
...
...
...
M
1
1
11
A
a
a
a
a
nm
n
m
a
ij
n
i
m
j
,...,
1
,...,
1

23.05.21
4
Przykłady macierzy
]
2
[
)
(liczba
skalarna
macierz
a
5
,
0
,
3
,
1
,
7
,...,
,
2
1
wierszowy
wektor
a
a
a
m
1
5
2
3
0
...
2
1
kolumnowy
wektor
a
a
a
n

23.05.21
5
Przykłady macierzy cd.
2
2
kwadratowa
macierz
4
3
2
1
x
n
stopnia
a
jednostkow
macierz
1
...
0
0
...
...
...
...
0
...
1
0
0
...
0
1
Macierz jednostkową stopnia n
oznaczamy I
n

23.05.21
6
Przykłady macierzy dok.
rozmiarów
dowolnych
zerowa
macierz
0
...
0
...
...
...
0
...
0
0
...
0
2
3
2
5
0
2
7
4
0
0
1
3
0
0
0
2
macierz trójkątna
dolna

23.05.21
7
Działania na macierzach
M
m
n
x
ij
ij
ij
ij
nxm
b
a
b
a
M
B
A,
macierzy
Dodawanie
:
2
1
2
2
2
0
6
4
1
2
3
2
4
3
1
0
1
2
Dodawanie macierzy jest przemienne i
łączne, a macierz zerowa (odpowiedniego
rozmiaru) jest jego zerem.
Przykład

23.05.21
8
Działania na macierzach cd.
Mnożenie macierzy A przez liczbę c
nxm
dla
ij
ij
M
A
a
c
a
c
A
c
18
6
12
3
9
6
)
6
(
3
2
3
)
4
(
3
1
3
3
3
)
2
(
3
6
2
4
1
3
2
3
Przykład

23.05.21
9
Działania na macierzach cd.
Transponowanie macierzy
6
5
4
3
2
1
6
4
2
5
3
1
A
Dla
,...,
1
,...,
1
,...,
1
,...,
1
A
T
x
m
j
n
i
T
n
i
m
j
M
a
a
n
m
ji
ij
Przykład

23.05.21
10
Działania na macierzach dok.
m
i
il
ki
ml
m
l
k
l
k
kl
b
a
b
a
b
a
b
a
c
M
C
B
A
M
B
M
A
nxp
mxp
nxm
:
konieczny
Warunek
1
1
2
2
1
1
...
,
(zasada mnożenia ”wiersze przez kolumny”)
Mnożenie macierzy jest łączne ale
nieprzemienne. Jeśli AB istnieje to BA
niekoniecznie, a jeśli nawet istnieją oba iloczyny
to zazwyczaj nie są równe. Zawsze można
mnożyć przez siebie macierze kwadratowe tego
samego stopnia
Mnożenie macierzy A i B przez siebie

23.05.21
11
Mnożenie macierzy - przykłady
2
0
1
3
2
1
1
1
2
1
0
1
1
1
2
1
0
1
2
0
1
3
2
1

23.05.21
12
Macierz odwrotna
Jeśli dwie macierze kwadratowe A i B tego samego
stopnia n spełniają równość:
AB = I
n
to macierz B nazywamy
odwrotną
do A i
oznaczamy
B = A
-1
I
2
1
0
0
1
1
1
0
1
1
1
0
1
Macierz, dla której istnieje macierz odwrotna nazywamy
nieosobliwą.

23.05.21
13
Podmacierz macierzy A
•
Podmacierzą
(
minorem
) stopnia r
x
k
macierzy A stopnia n
x
m nazywamy macierz
powstałą z macierzy A przez skreślenie jej n –
r wierszy oraz m – k kolumn
•Macierz powstającą przez skreślenie i-tego
wiersza i j-tej kolumny macierzy M
oznaczamy:
ij
M

23.05.21
14
Podmacierze cd.
2
4
1
0
1
2
2
4
2
1
0
2
3
1
1
1
2
1
12
A
A

23.05.21
15
Wyznacznik macierzy kwadratowej
• Każdej macierzy kwadratowej A możemy przypisać
jednoznacznie pewną liczbę, zwaną
wyznacznikiem
i oznaczaną det A lub |A|.
Wyznacznik jest określony indukcyjnie jak następuje:
- det [a] = a
- jeśli A M
n
i n>1 to :
A
a
A
a
kj
n
j
j
k
kj
il
n
i
l
i
il
A
det
det
det
1
)
(
1
)
(
)
1
(
)
1
(
• Wzór ten nosi nazwę
rozwinięcia
Laplace’a
względem l – tej kolumny (k – tego
wiersza)
;

23.05.21
16
Obliczanie wyznaczników -
przykład
ceg
bdi
afh
cdh
bfg
aei
ec
bf
g
hc
bi
d
fh
ei
a
i
f
c
h
e
b
g
d
a
bc
ad
d
c
b
a
)
(
)
(
)
(
det
det

23.05.21
17
Dopełnieniem algebraicznym
elementu a
ik
nazywamy liczbę
równą iloczynowi minora M
ik
odpowiadający temu elementowi
przez (-1)
i+k
ij
k
i
ik
M
A
)
1
(

23.05.21
18
Własności wyznaczników
1. det (A·B) = det A·det B
2. det (A
-1
) = 1/det A
3. det A
T
= det A
4. det I
n
=1
5. Wyznacznik macierzy trójkątnej jest równy
iloczynowi elementów na przekątnej
macierzy.
8
2
2
)
1
(
2
2
3
2
5
0
2
7
4
0
0
1
3
0
0
0
2
det

23.05.21
19
Własności wyznaczników
cd. – operacje
elementarne
6.
Zamiana miejscami dwóch kolumn (wierszy)
macierzy zmienia znak wyznacznika
7.
Pomnożenie wszystkich elementów jednego
wiersza (jednej kolumny) macierzy przez k
powoduje pomnożenie wartości
wyznacznika przez ten sam czynnik k.
8.
Odjęcie od jednego wiersza (kolumny)
macierzy innego wiersza (kolumny), ew.
pomnożonego przez stałą, nie zmienia
wartości wyznacznika

23.05.21
20
Macierz odwrotna a wyznacznik
Macierz odwrotna istnieje tylko wtedy, jeśli dana
macierz ma wyznacznik różny od zera. Jeśli
zatem warunek ten jest spełniony to macierz
odwrotna istnieje i można ją przedstawić w
postaci
D
A
A
A
det
1
1
Macierz A
D
macierzą dołączoną –
transponowaną macierzą dopełnień
algebraicznych

23.05.21
21
Rząd macierzy
Rzędem macierzy
nazywamy rozmiar
największego niezerowego wyznacznika tej
macierzy, tj. rozmiar jej największej
kwadratowej podmacierzy o wyznaczniku
różnym od zera. Rząd macierzy A oznaczamy
rz A.
2
8
2
3
3
3
1
1
1
5
1
4
2
rz

23.05.21
22
Układy równań liniowych
Układem n równań liniowych z m
niewiadomymi
nazywamy zbiór wyrażeń postaci:
b
x
a
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
n
m
nm
n
n
m
m
m
m
...
...
...
...
2
2
1
1
2
2
2
22
1
21
1
1
2
12
1
11
Wyrazy a
ij
nazywamy
współczynnikami
układu, wyrazy x
j
– zmiennymi a wyrazy b
i
–
wyrazami
wolnymi
. Jeśli wszystkie wyrazy b
i
są
równe zero to układ taki nazywamy
jednorodnym
.

23.05.21
23
Układy równań –
przykłady
2
2
0
4
3
2
t
y
x
t
z
y
x
z
y
x
Układ I niejednorodny 3 równań z 4
niewiadomymi
Układ II jednorodny 3 równań z 2
niewiadomymi
0
5
0
4
0
2
y
x
y
x
y
x
23.05.21
24
Układy równań liniowych
Macierze A, X i B mają postać
mn
m
m
n
n
a
a
a
a
a
a
a
a
a
A
2
1
2
22
21
1
12
11
n
x
x
x
X
2
1
m
b
b
b
B
2
1
Macierz
główna Macierz
niewiadomych
Macierz wyrazów wolnych

23.05.21
25
Macierzowy zapis układu
równań
W zapisie macierzowym układ równań można
przedstawić w postaci
AX=B
gdzie
:
x1
x1
x
n
m
m
n
B
X
b
x
a
A
i
j
ij
,
,
Macierz A nazywamy
macierzą układu
,
macierz B
-
macierzą wyrazów wolnych
, zaś
macierz [A|B] =
A
+
tj. macierz A z dołączoną na końcu
kolumną
wyrazów wolnych -
macierzą
rozszerzoną układu
.

23.05.21
26
Macierzowy zapis układu
równań cd.
2
0
4
1
0
1
2
1
1
1
1
0
1
3
2
t
z
y
x
0
0
0
5
1
1
4
1
2
y
x

23.05.21
27
Rozwiązanie układu równań
liniowych
Jeśli układ równań liniowych nie ma rozwiązań
to nazywamy go
sprzecznym
, w przeciwnym
zaś przypadku nazywamy go
rozwiązalnym
.
• Układ rozwiązalny mający dokładnie jedno
rozwiązanie nazywamy
oznaczonym
, zaś
mający więcej niż jedno rozwiązanie –
nieoznaczonym
.
Przykład: układ jednorodny jest zawsze
rozwiązalny – jednym z rozwiązań jest wektor
[0, 0, …, 0].

23.05.21
28
Istnienie i jednoznaczność
rozwiązania układu równań
liniowych
• Warunkiem koniecznym i dostatecznym
rozwiązalności układu równań liniowych
jest spełnianie równości
rz A = rz A
+
= k
• Jeśli ponadto k = m (liczba niewiadomych)
to układ jest oznaczony, w przeciwnym
wypadku jest nieoznaczony i rozwiązania
stanowią zbiór zależny od (n – k)
parametrów.

23.05.21
29
Metody rozwiązywania układów
równań
Wyróżniamy następujące metody
rozwiązywania układów równań:
metodę graficzną
metodę podstawień
metodę operacji elementarnych
metodę macierzową
metodę wyznaczników
Omówimy teraz niektóre z tych
metod.

23.05.21
30
Układ n równań liniowych z n niewiadomymi
W zapisie macierzowym ma on postać
Macierz współczynników A jest macierzą
nieosobliwą, tzn. det A 0 (wyznacznik
macierzy A jest różny od zera).
Istnieje więc macierz odwrotna A
-1
. W celu
rozwiązania układu mnożymy obie strony
równania (13) lewostronnie przez macierz A
-1
i
otrzymujemy
n
n
nn
n
n
n
n
n
n
b
x
a
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
2
2
1
1
2
2
2
22
1
21
1
1
2
12
1
11
Ax = b
x= A
-1
b

23.05.21
31
Wzory Cramera:
Wyznacznik W
1
powstaje przez wstawienie kolumny
wyrazów wolnych do pierwszej kolumny
wyznacznika W
Wyznacznik W
2
powstaje przez wstawienie
kolumny wyrazów wolnych do drugiej kolumny
wyznacznika W
Wyznacznik główny W powstaje z elementów
macierzy A
W
W
x
W
W
x
2
2
1
1
,
Rozwiązywanie układu n równań z n
niewiadomymi
Metoda wyznaczników
2
2
22
1
21
1
2
12
1
11
b
x
a
x
a
b
x
a
x
a
23.05.21
32
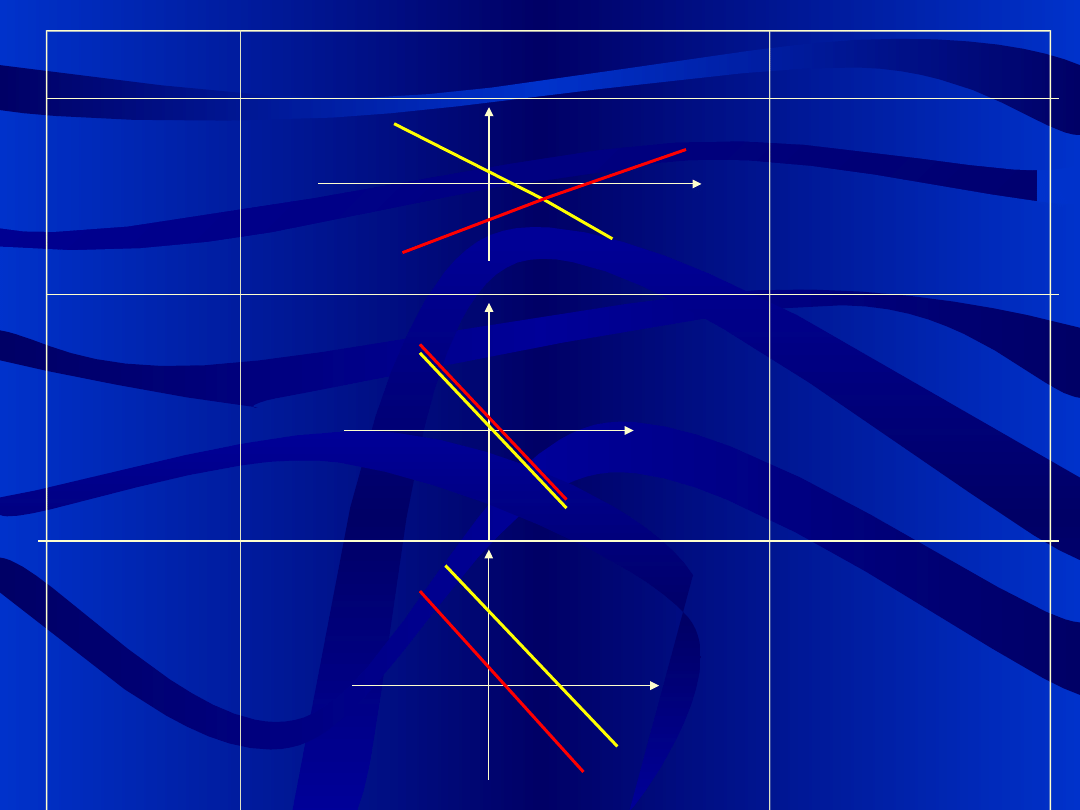
Liczba
rozwiązań
Układ posiada 1
rozwiązanie-
UKŁAD
OZNACZONY
Układ posiada
nieskończenie
wiele
rozwiązań-
UKŁAD
NIEOZNACZO
NY
Układ nie
posiada
rozwiązania-
UKŁAD
SPRZECZNY
Interpretacja geometryczna
Założenia
0
W
0
0
0
Y
X
W
W
W
x
y
x
y
0
0
0
0
Y
X
W
W
W
W
x
y

23.05.21
33
Układ 3 równań liniowych
Wzory Cramera:
3
3
33
2
32
1
31
2
3
23
2
22
1
21
1
3
13
2
12
1
11
b
x
a
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
(7)
W
W
x
W
W
x
W
W
x
3
3
2
2
1
1
,
,
(8)
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
Wyszukiwarka
Podobne podstrony:
Wyklad Nr 1 UKLADY ROWNAN LINIOWYCH
Zestaw 12 Macierz odwrotna, układy równań liniowych
lab8 1 uklady rownan liniowych
Układy równań liniowych
2011 lab 02, Uklady rownan liniowych
Układy równań liniowych
układy równań liniowych 2
Układy równań liniowych z parametrem
Matematyka I (Ćw) Lista 05 Układy m równań liniowych z n niewiadomymi
Układy równań liniowych, Matematyka dla ekonomistów
Uklady rownan liniowych
02. Układy równań liniowych
2011 lab 02 Uklady rownan liniowychid 27450
02 Układy równań liniowychid 3448
Zestaw uklady rownan liniowych
Układy równań liniowych z trzema niewiadomymi
Układy równań liniowych
matematyka, Układy równań liniowych, Układy równań liniowych o dwóch niewiadomych
6-MACIERZE, WYZNACZNIKI, UKŁADY RÓWNAŃ LINIOWYCH, MACIERZE I WYZNACZNIKI
więcej podobnych podstron