UKŁADY

RÓWNAŃ

LINIOWYCH

Z

TRZEMA

NIEWIADOMYMI

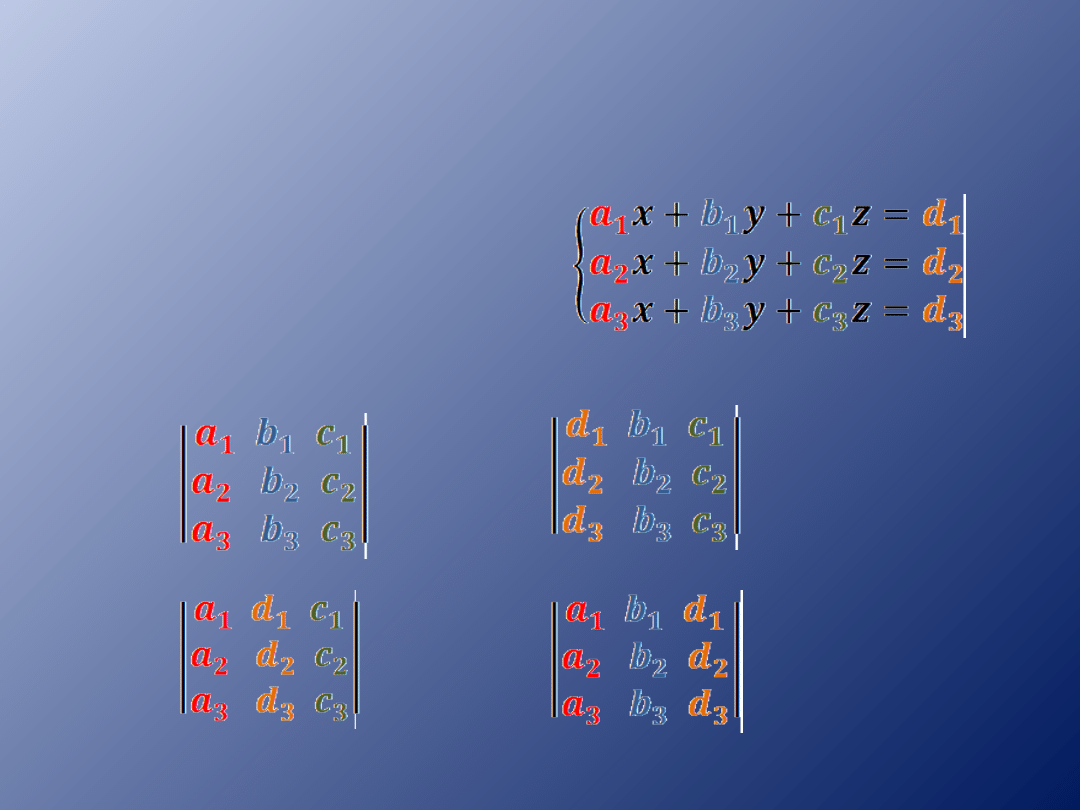
DEFINICJE:
Układ równań liniowych
z trzema niewiadomymi
można rozwiązać
stosując
metodę wyznaczników:

W=

Wy=

Wx=

Wz=

Zajmiemy się rozwiązaniem układu równań z
trzema niewiadomymi.

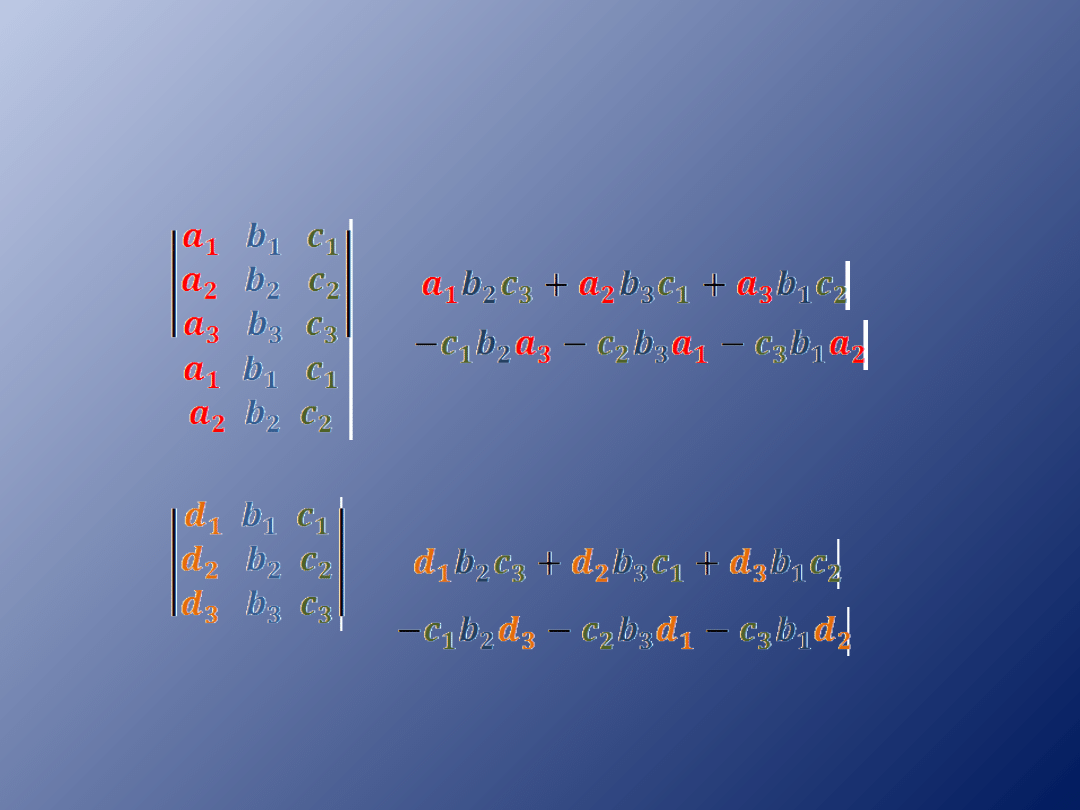
Pod wyznacznikiem dopisujemy pierwszy

wiersz, pod nim drugi wiersz, tworzymy

sześć iloczynów.

W= =

Wx=
=

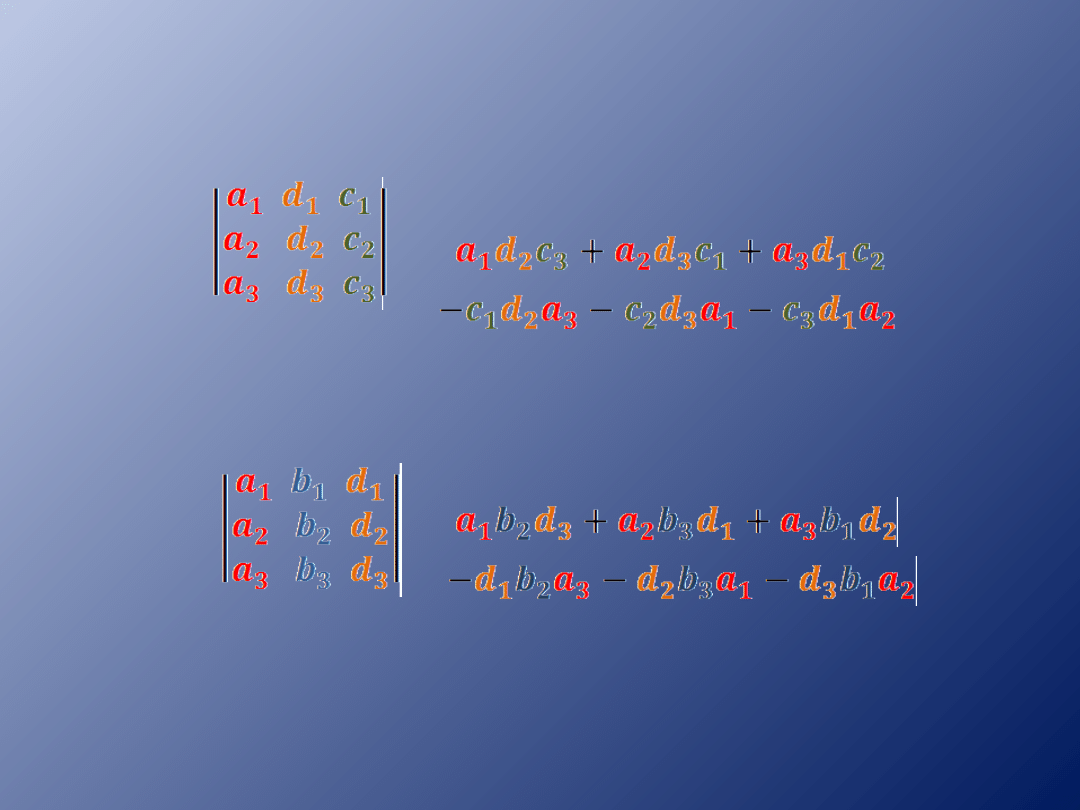
Wy=
=

Wz=
=

Jeżeli:

a)W

≠ 0 to trójka liczb (x,y,z) jest jedynym

rozwiązaniem układu równań (równania układu są

niezależne)

b)

W = 0 to układ może nie mieć rozwiązań

(równania układu są sprzeczne) albo może mieć

nieskończenie wiele rozwiązań zależnych albo od

jednego parametru albo od dwóch parametrów

(równania układu są zależne).

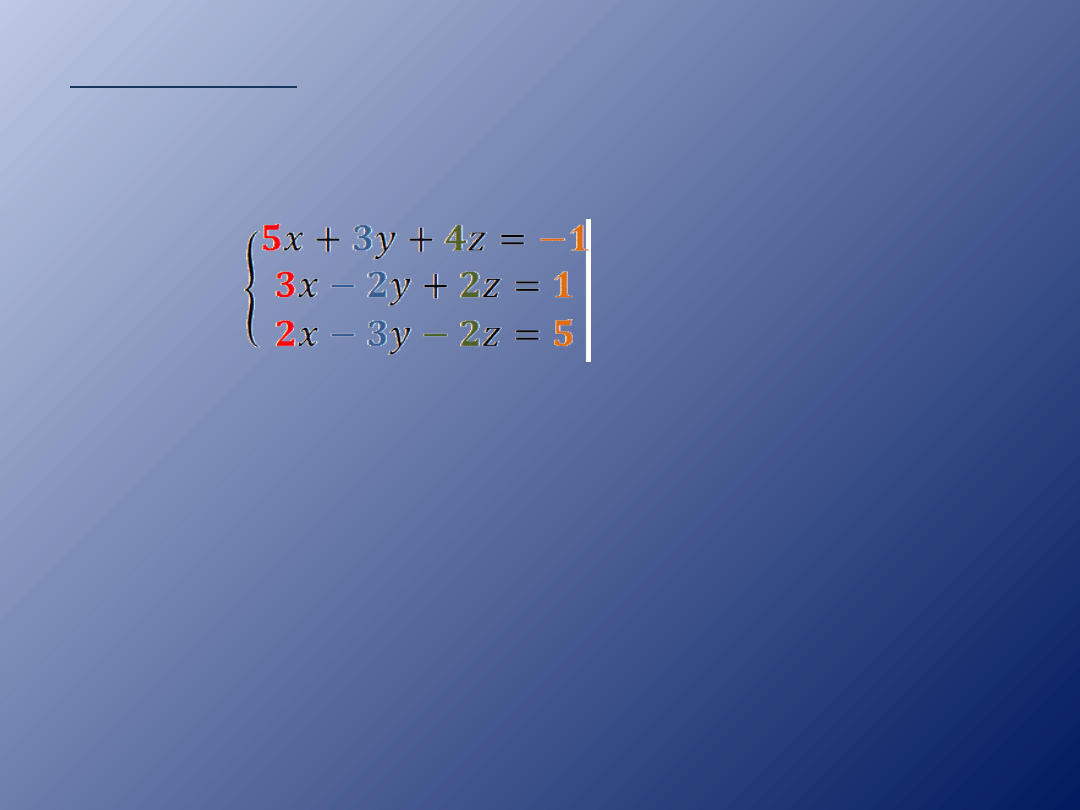
Przykład 1.
Rozwiąż układ równań:

Obliczamy wyznacznik W, wyznaczniki Wx,

Wy, Wz.

Tworzymy kolumny z liczb znajdujących się

przed odpowiedniki niewiadomymi.

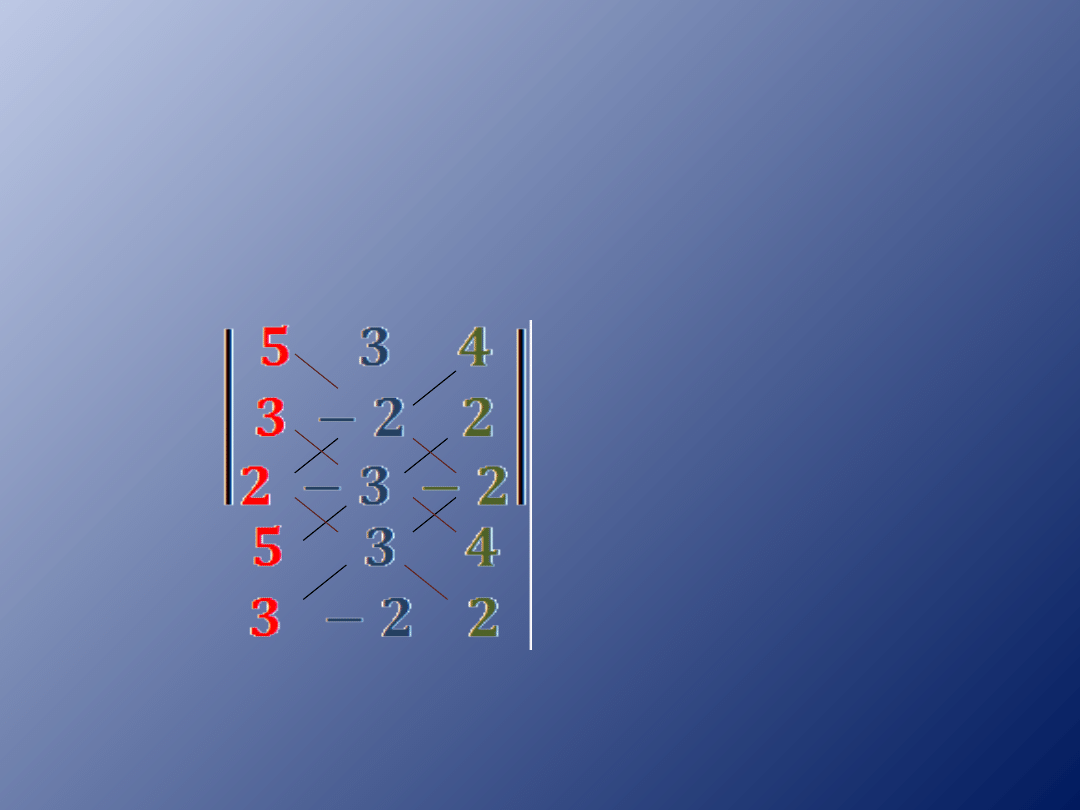
Dopisujemy dwa pierwsze wiersze i obliczamy

wyznacznik mnożąc odpowiednie liczby po

przekątnej – najpierw wg bordowych linii,

potem wg czarnych linii zmieniając znak na

przeciwny.

W =

W =

5

·

(-2)

·

(-2)

+

3

·

(

-

3)

·

4

+

2

·

3

·

2

-

4

·

(-2)

·

2

-

2

·

(-3)

·

5

-

(-

2)

·

3

·

3

=

= 20-36+12+16+30+18=60

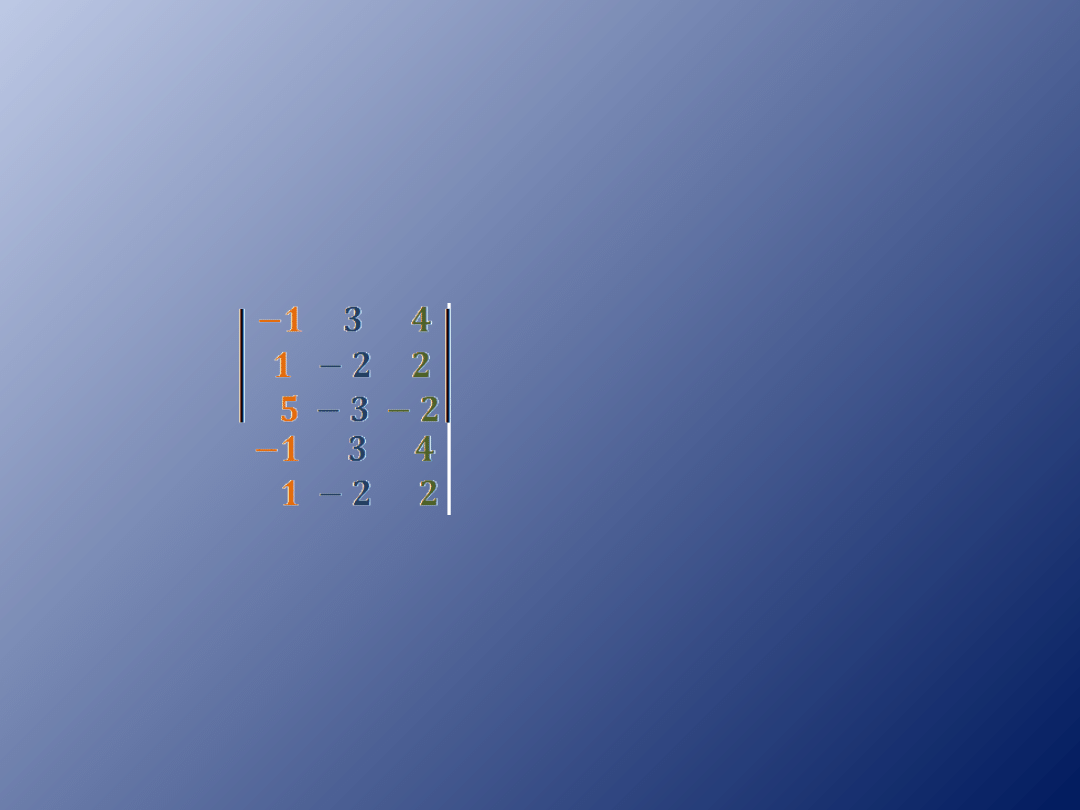
Obliczamy wyznacznik Wx – tworzymy

kolumnę liczb wolnych oraz kolumny liczb

znajdujących się przed niewiadomą y i z.

Wx=

Wx =

(-1)

·

(-2)

·

(-2)

+

1

·

(

-

3)

·

4

+

5

·

3

·

2

-

4

·

(-2)

·

5

-

2

·

(-3)

·

(-1)

-

(-

2)

·

3

·

1

=

= -4-12+30+40-6+6=54

Obliczamy wyznacznik Wy – tworzymy

kolumnę liczb wolnych oraz kolumny liczb

znajdujących się przed niewiadomą x i z.

Wy=

Wy =

5

·

1

·

(-2)

+

3

·

5

·

4

+

2

·

(-1)

·

2

-

4

·

1

·

2

-

2

·

5

·

5

-

(-2)

·

(-1)

·

3

=

= -10+60-4-8-50-6=-18

Obliczamy wyznacznik Wz – tworzymy

kolumnę liczb znajdujących się przed

niewiadomą x i y oraz kolumnę liczb

wolnych.

Wz=

Wz =

5

·

(-2)

·

5

+

3

·

(

-

3)

·

(-1)

+

2

·

3

·

1

-

(-1)

·

(-2)

·

2

-

1

·

(-3)

·

5

-

5

·

3

·

3

=

= -50+9+6-4+15-45=-69

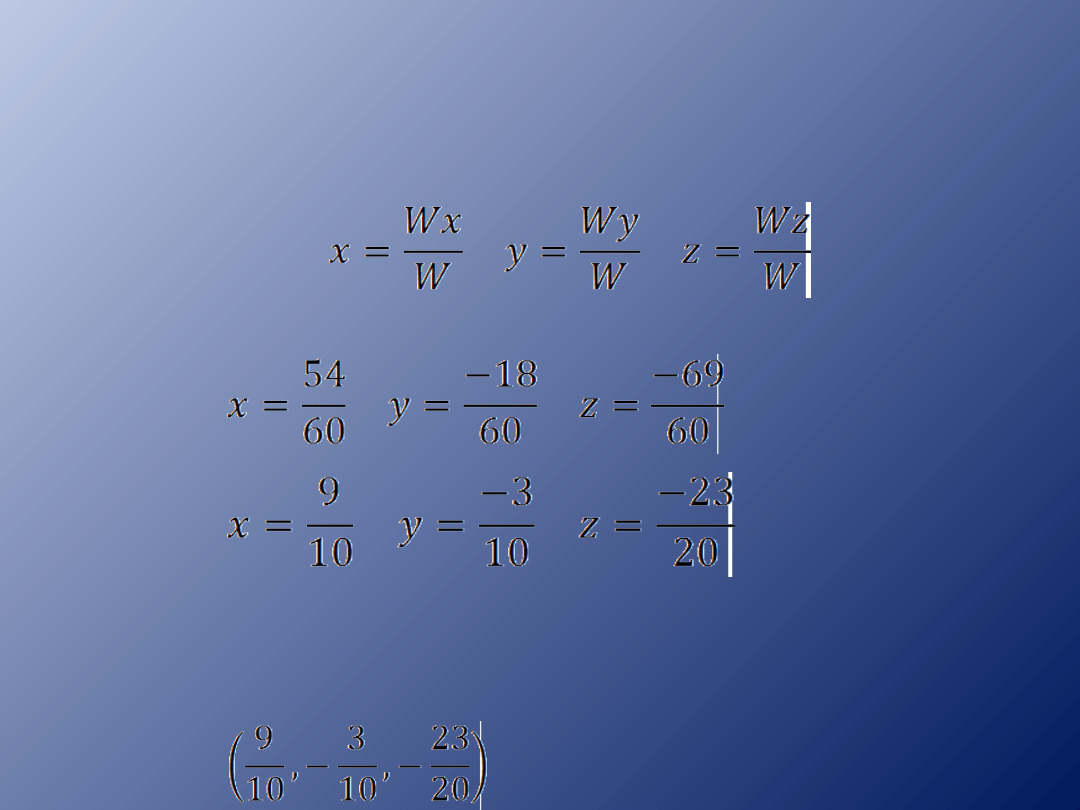
Wyznacznik główny W jest różny od zera,

dlatego układ równań ma jedno rozwiązanie,

które obliczamy ze wzoru:

Zbiorem rozwiązań układu równań jest trójka

liczb:

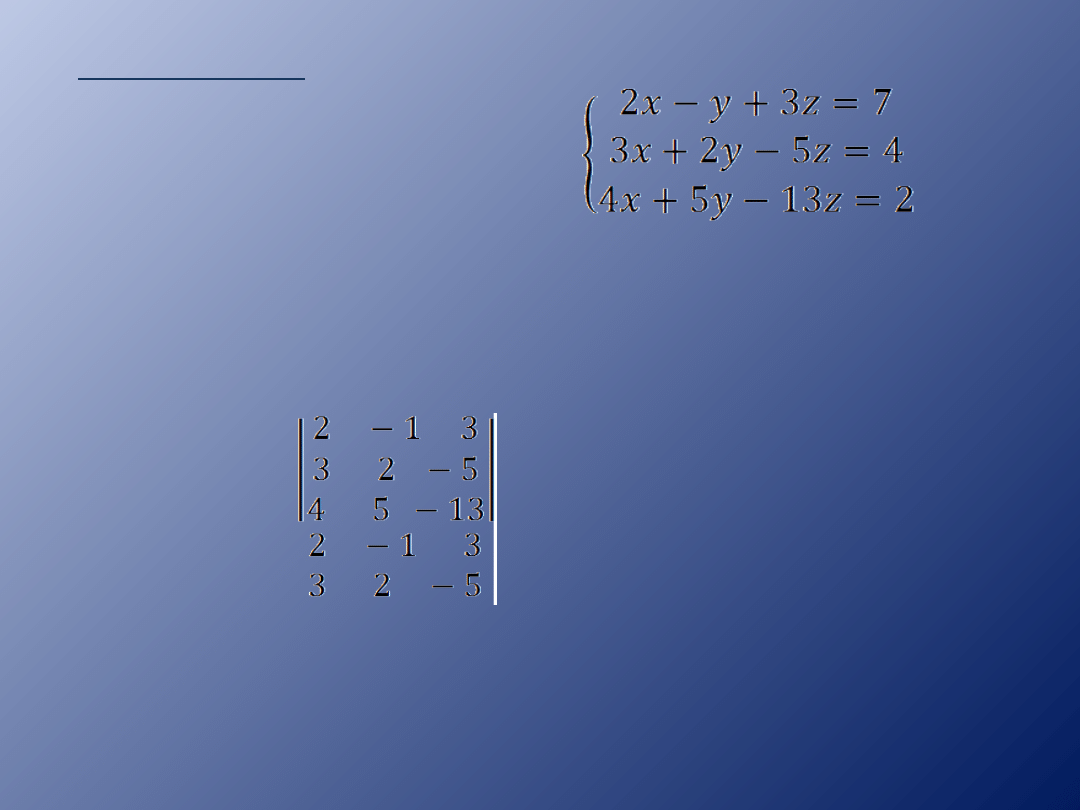
Przykład 2.
Metodą wyznacznikową
rozwiąż układ równań:

Obliczamy wyznacznik W
oraz wyznaczniki: Wx, Wy,
Wz

W=

W = -52+45+20-24+50-39 = 0

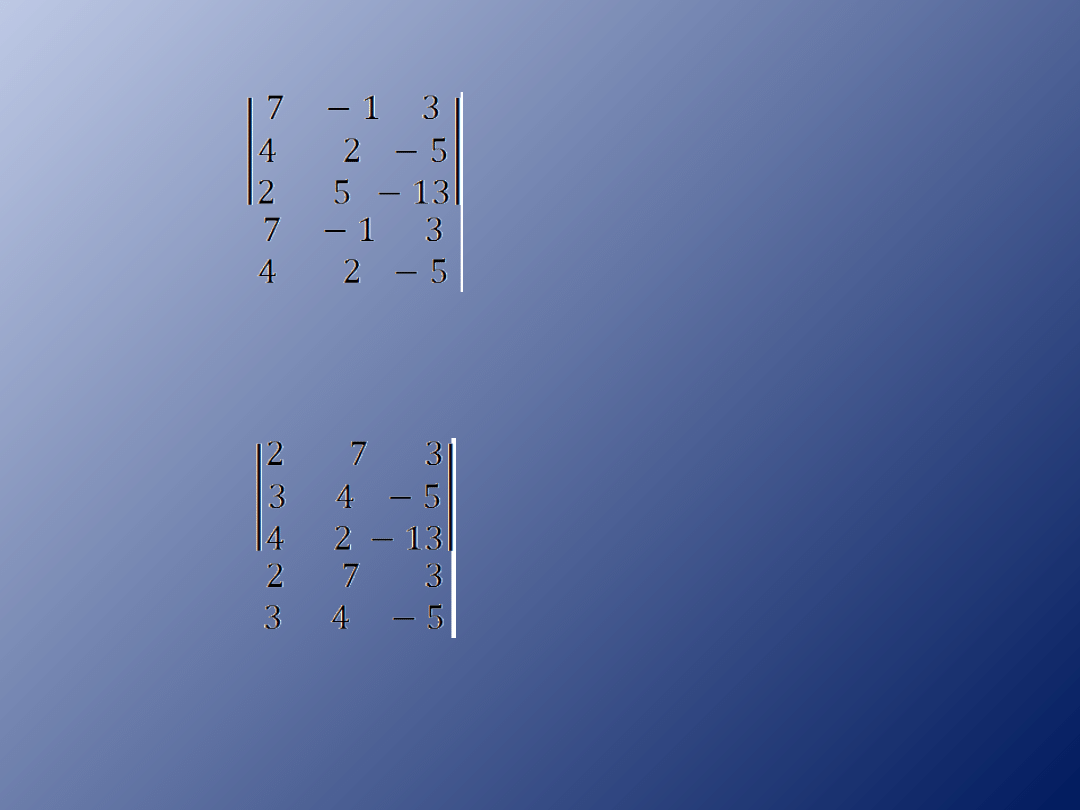
Wx = -182+60+10-12+175-52=-1

Wx =

Wy =

Wy = -104+18-140-48+20+273=19

Wz = 8+105-16-56-40+6=7

Wz =

Wyznacznik W ma wartość 0, wyznaczniki Wx,

Wy, Wz są różne od 0.

Układ równań nie posiada żadnych rozwiązań,

jest sprzeczny.

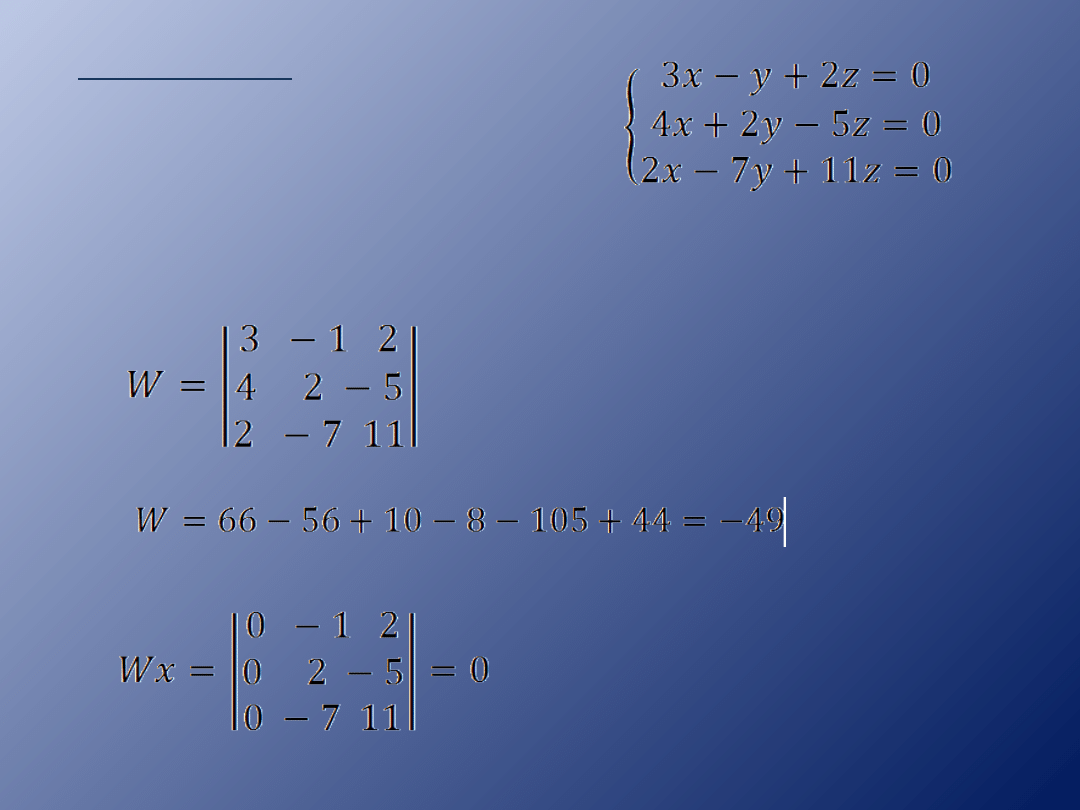
Przykład 3
Rozwiąż układ równań:

Obliczamy wyznacznik W
oraz wyznaczniki: Wx, Wy,
Wz

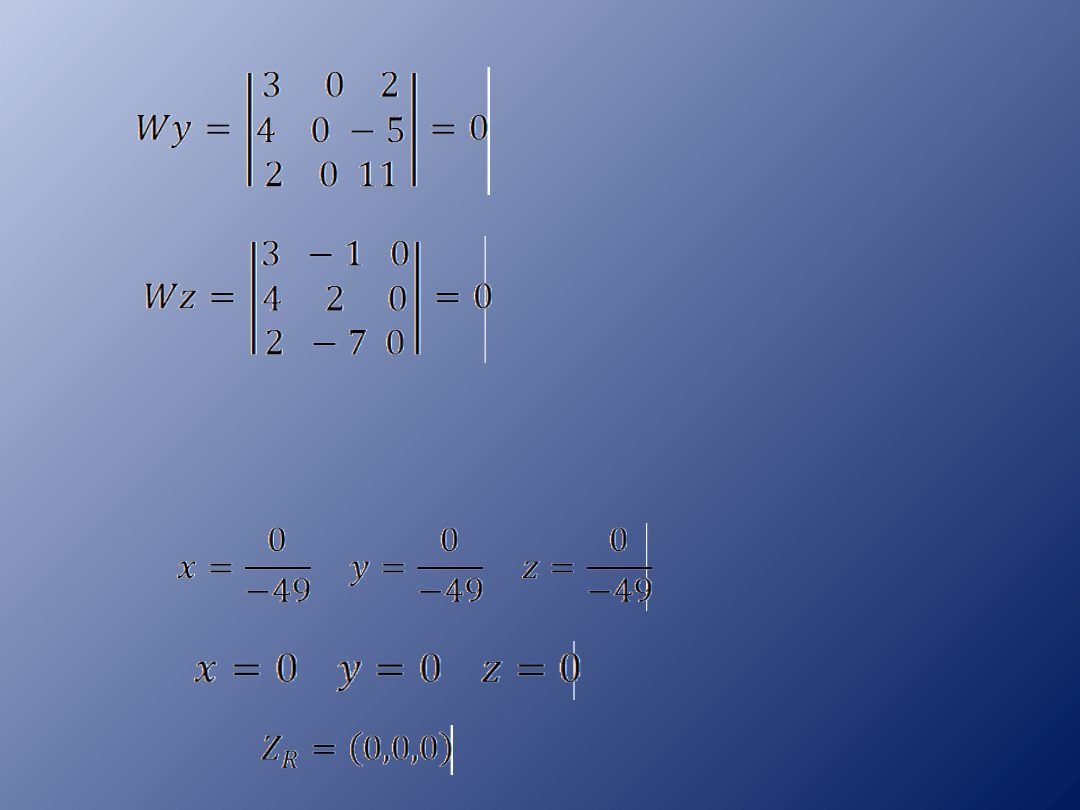
Wyznacznik W jest różny od 0, więc układ
ma jedno rozwiązanie postaci:

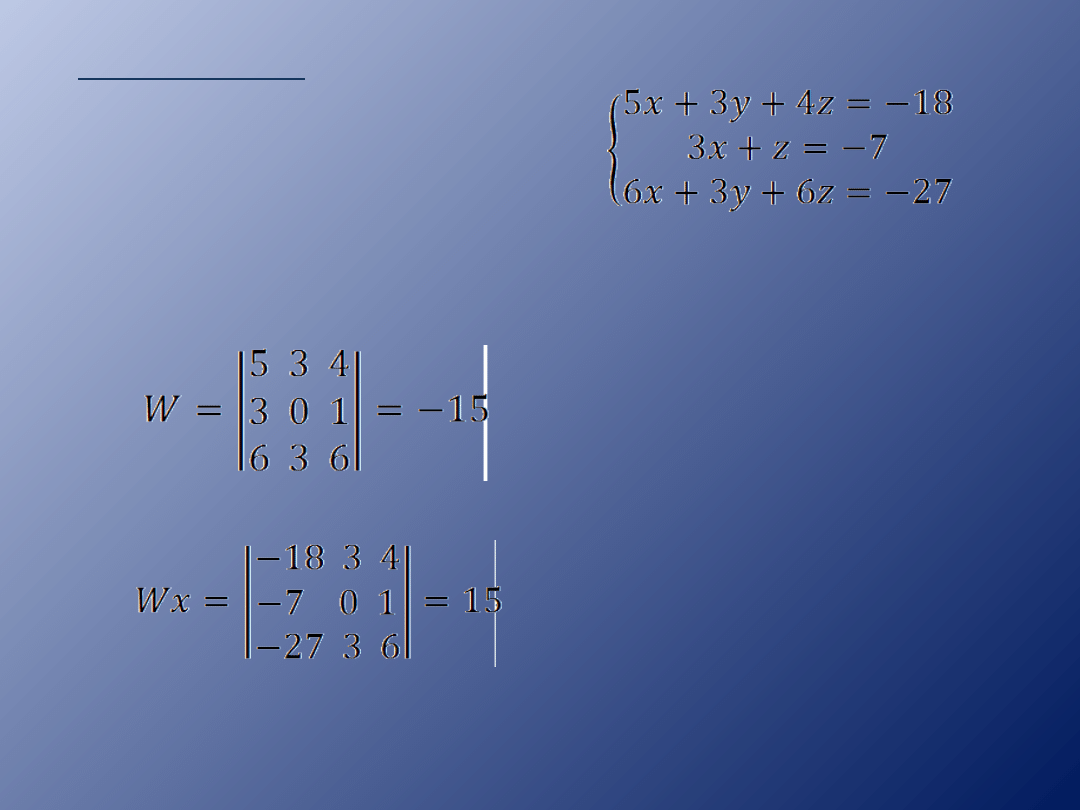
Przykład 4.
Rozwiąż układ równań:

Obliczamy wyznacznik W
oraz wyznaczniki: Wx, Wy,
Wz

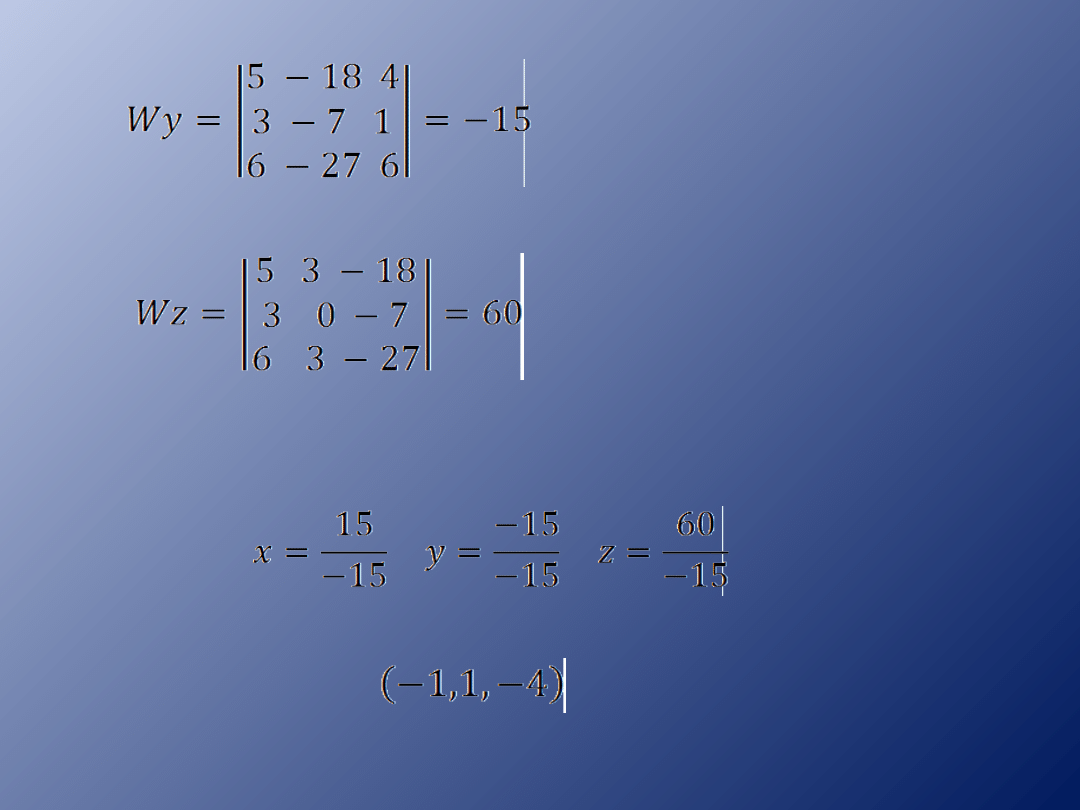
Wyznacznik W jest różny od 0, więc układ
ma jedno rozwiązanie postaci:

Zr={ }