1

Układy równań liniowych

Definicja Układem

m

równań z

n

niewiadomymi

x

1

, x

2

, . . . , x

n ,

gdzie

m, n ∈ N

, nazywamy układ równań postaci:

(∗)







































































































a

11

x

1

+

a

12

x

2

+ . . .

+

a

1n

x

n

= b

1

a

21

x

1

+

a

22

x

2

+ . . .

+

a

2n

x

n

= b

2

. . .

. . .

. . .

. . .

. . .

a

m1

x

1

+ a

m2

x

2

+ . . .

+ a

mn

x

n

= b

m

gdzie

a

ij

∈ R

nazywamy współczynnikami układu,

b

i

∈ R

nazywamy wyrazami wolnymi (

i = 1, 2, . . . , m

,

j = 1, 2, . . . , n

).

2

Definicja

• Rozwiązaniem układu równań

(∗)

nazywamy ciąg liczb rzeczywistych

x

1

, x

2

, . . . , x

n , spełniających ten układ.

• Układ, który nie posiada rozwiązania nazywamy układem sprzecznym.

Uwaga

Układ

(∗)

można zapisać w postaci macierzowej:

A X = B,

gdzie

A =





























a

11

a

12

. . .

a

1n

a

21

a

22

. . .

a

2n

. . .

. . .

. . .

. . .

a

m1

a

m2

. . .

a

mn





























X =





























x

1

x

2

. . .

x

n





























B =





























b

1

b

2

. . .

b

m





























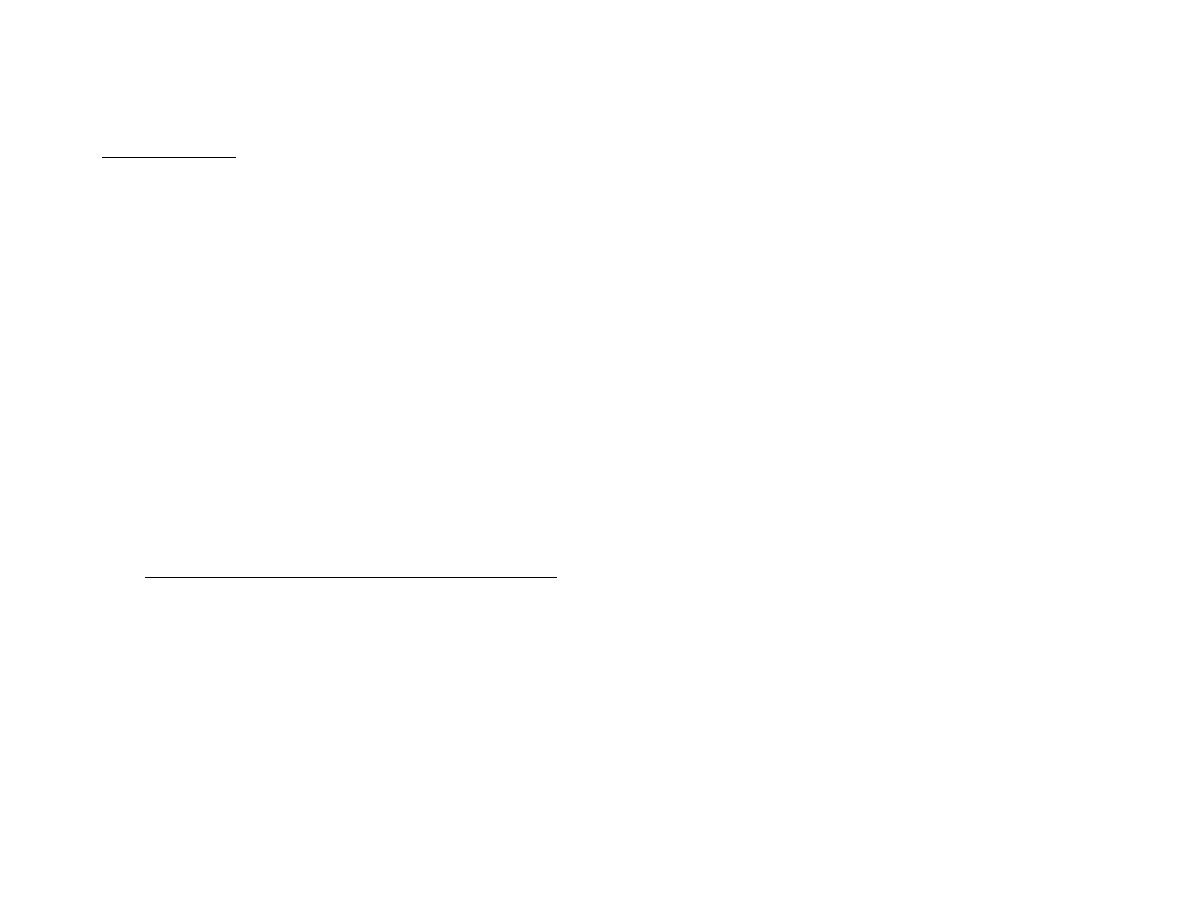
3

Definicja

• Macierz

A

nazywamy macierzą główną układu równań

(∗)

.

• Macierz

X

nazywamy macierzą (kolumną) niewiadomych.

• Macierz

B

nazywamy macierzą (kolumną) wyrazów wolnych.

Rozwiązywanie układów równań liniowych

1) Metoda mcierzy odwrotnej

Jeżeli

m = n

i

det A 6= 0

, czyli macierz główna układu

(∗)

jest macierzą kwadratową nieosobliwą (tym samym istnieje macierz

odwrotna

A

−1

), to rozwiązania układu

(∗)

możemy poszukiwać

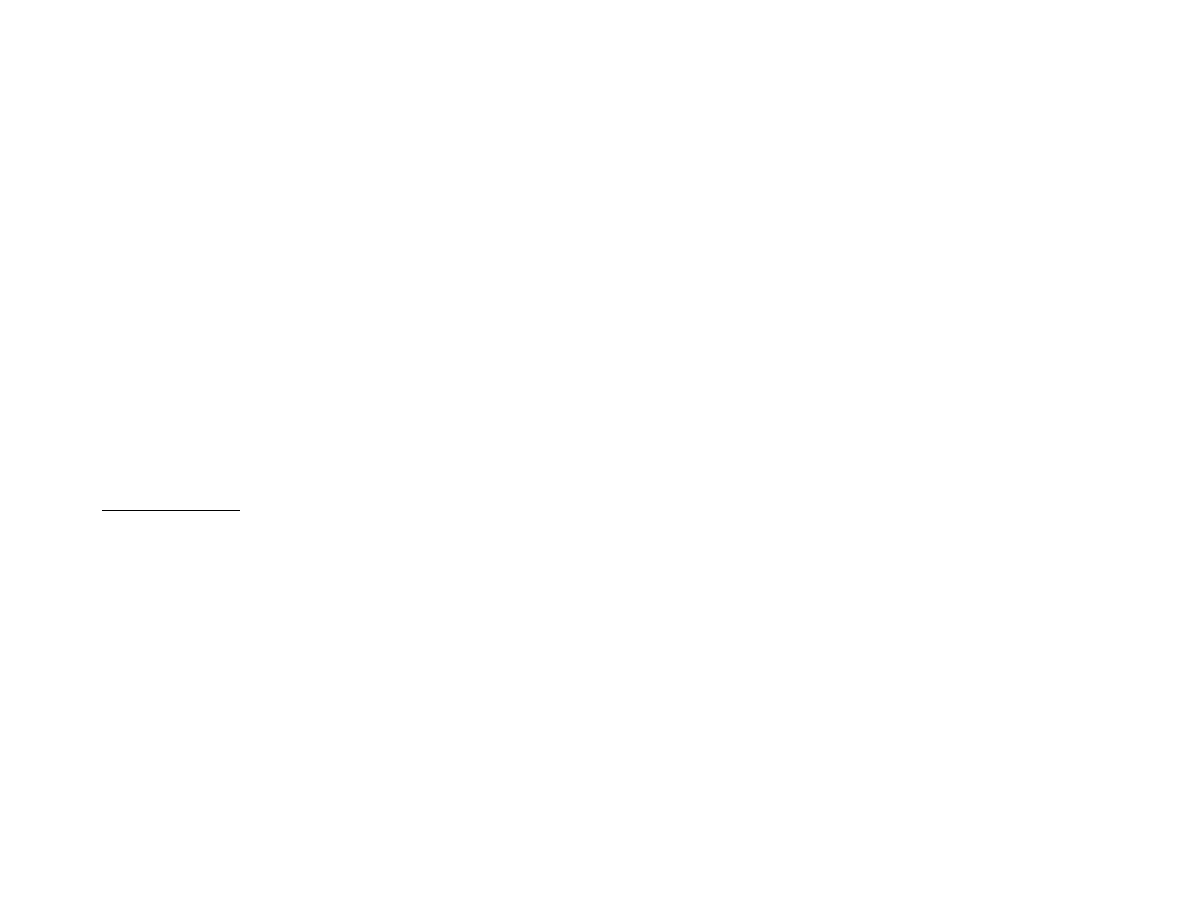
4

jako rozwiązania równania macierzowego

A X = B,

tzn.

X = A

−1

B.

Przykład

Metodą macierzy odwrotnej rozwiąż układ równań:







































































x

+ y − 2z

= 3

y −

z

= −1

−x

+ 2z

= 5

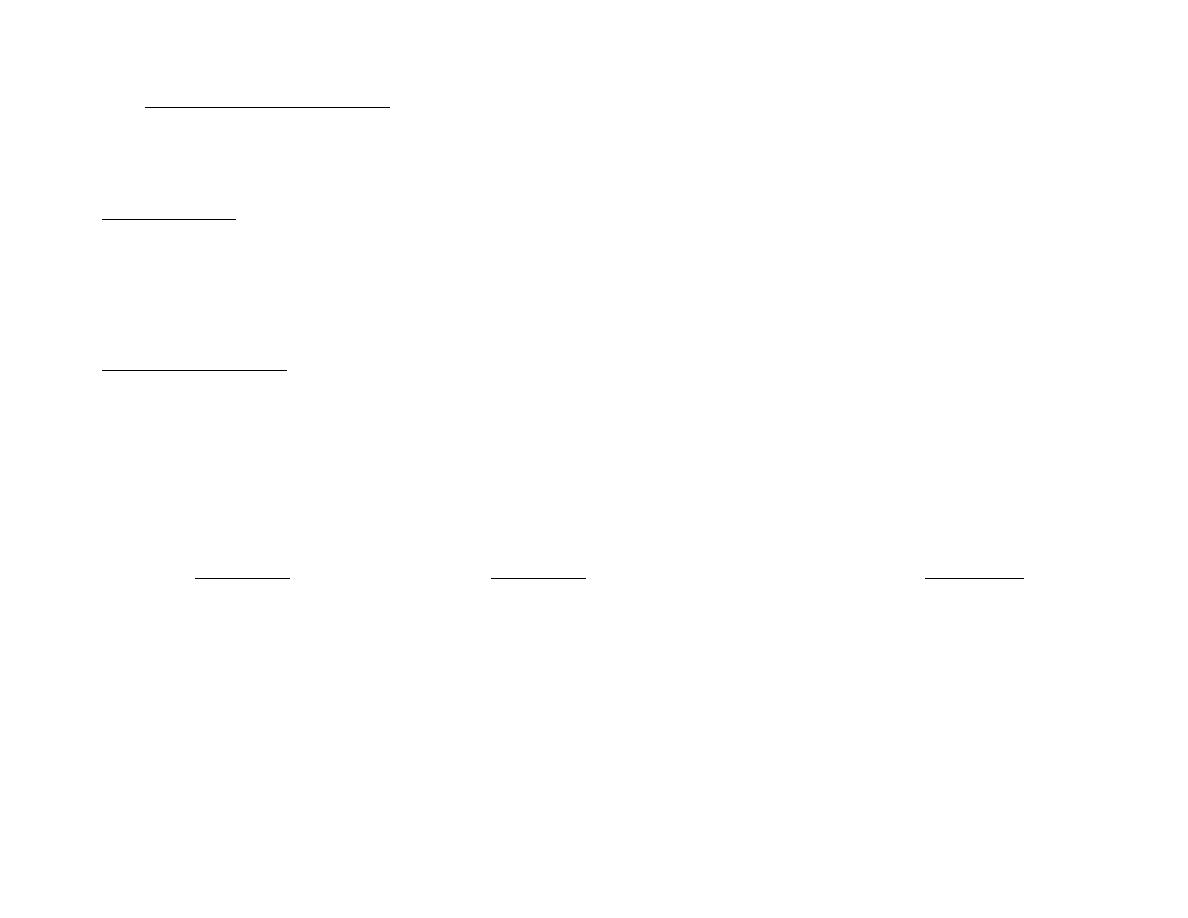
5

2) Wzory Cramera

Definicja

Układ

(∗)

nazywamy układem Cramera, jeżeli macierz

główna

A

tego układu jest macierzą kwadratową nieosobliwą.

Twierdzenie

(Cramera)

Układ Cramera ma dokładnie jedno rozwiązanie. Rozwiązanie to

dane jest wzorami (Cramera):

x

1

=

det A

1

det A

,

x

2

=

det A

2

det A

,

. . . ,

x

n

=

det A

n

det A

,

gdzie macierz

A

i

dla

i = 1, 2, . . . , n

powstaje z macierzy

A

w

wyniku zastąpienia kolumny współczynników stojących przy niewiadomej

x

i kolumną wyrazów wolnych.

6

Przykład

Wyznacz

x

2 z układu równań:







































































































2x

1

− 2x

2

+

x

3

+ 3x

4

= 5

x

1

+ 3x

2

−

x

3

+

x

4

= 6

3x

1

−

x

2

−

x

3

+

x

4

= 6

x

1

+

x

2

+ 2x

3

−

x

4

= 2

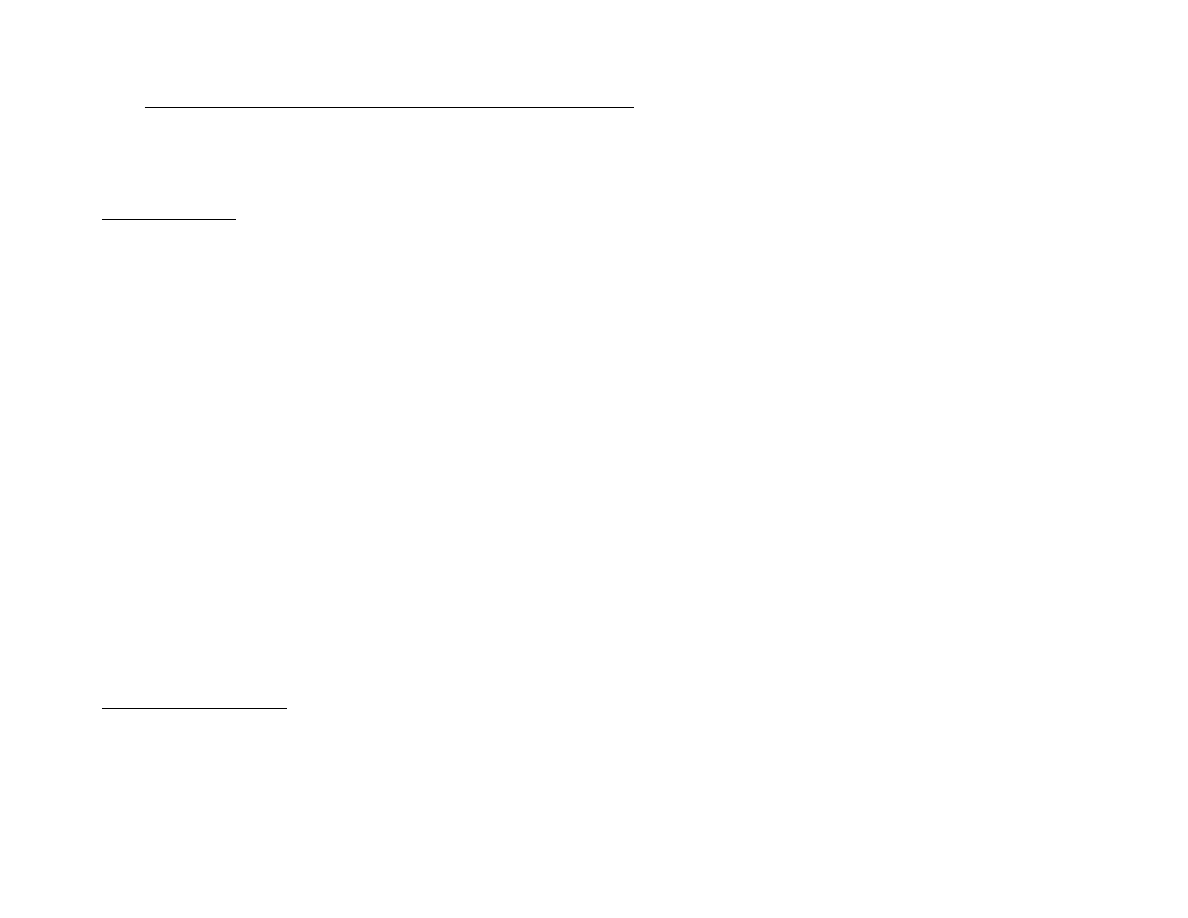
7

3) Twierdzenie Kroneckera-Capelli

Rozważmy układ

(∗)

, gdzie w ogólności

m 6= n

.

Definicja

Macierz

U = A|B =





























a

11

a

12

. . .

a

1n

b

1

a

21

a

22

. . .

a

2n

b

2

. . .

. . .

. . .

. . .

. . .

a

m1

a

m2

. . .

a

mn

b

m





























nazywamy macierzą rozszerzoną układu

(∗)

.

Twierdzenie

(Kroneckera-Capelli)

Układ

(∗)

ma rozwiązanie wtedy i tylko wtedy, gdy

R(U) = R(A)

.

Co więcej:

8

• jeżeli

R(U) = R(A) = n

(

n

-liczba niewiadomych), to układ

(∗)

ma dokładnie jedno rozwiązanie,

• jeżeli

R(U) = R(A) = r < n

, to układ

(∗)

ma nieskończenie

wiele rozwiązań zależnych od

n − r

parametrów.

Przykład

Rozwiąż następujące układy równań:

a)











































3x − y +

z

= 2

x

+ y + 2z = 1

b)







































































x

−

y

+ 3z = 2

2x + 7y + 5z = 1

2x − 2y + 6z = −5

9

c)







































































































x

1

+ x

3

+ x

4

= 5

x

1

− x

2

+ x

3

= 1

x

2

+ x

3

− x

4

= 0

x

1

+ x

2

+ x

3

= 3

d)



































































































































3x

1

+ 2x

2

+ 2x

3

+ 2x

4

= 2

2x

1

+ 3x

2

+ 2x

3

+ 5x

4

= 3

9x

1

+

x

2

+ 4x

3

− 5x

4

= 1

2x

1

+ 2x

2

+ 3x

3

+ 4x

4

= 5

7x

1

+

x

2

+ 6x

3

−

x

4

= 7

10

Układy jednorodne

Definicja

Układ postaci

(∗)

nazywamy układem jednorodnym,

jeżeli macierz wyrazów wolnych tego układu jest macierzą zerową.

Fakt

Układ jednorodny ma zawsze rozwiązanie. Co więcej:

• jeżeli

R(A) = n

(

n

-liczba niewiadomych), to układ jednorodny

ma dokładnie jedno rozwiązanie postaci

x

1

= 0,

x

2

= 0,

. . . ,

x

n

= 0.

Rozwiązanie to nazywamy rozwiązaniem zerowm.

• jeżeli

R(A) = r < n

, to układ

(∗)

ma nieskończenie wiele

rozwiązań zależnych od

n − r

parametrów, przy czym zbiór

rozwiązań zawiera w sobie rozwiązanie zerowe.

11

Przykład

Dla jakich wartości parametru

a

układ ma rozwiązanie

niezerowe?







































































x

+ ay − 3z = 0

2x +

y

+

z

= 0

3x + ay −

z

= 0