08.12.2009

Twierdzenie 1

Jeżeli funkcja
,
są ciągłe w
, to funkcja
,
są też ciągłe w
.

Jeżeli ponad to
to
jest funkcją ciągłą w
.

Twierdzenie 2 o ciągłości superpozycji funkcji ciągłych

Jeżeli funkcja wewnętrzna
jest ciągła w
, a funkcja
jest ciągła
to funkcja złożona
jest ciągła w
.

Definicja

Niech funkcja
będzie określona dla
,

Mówimy, że funkcja
jest prawostronnie ciągła w
jeżeli

Niech funkcja
będzie określona dla
,

Mówimy, że funkcja
jest lewostronnie ciągła w
jeżeli

Definicja

Mówimy, że funkcja
jest ciągła na przedział domknięty
jeżeli funkcja
jest ciągła w każdym punkcie
oraz prawostronnie ciągła w

i lewostronnie ciągła

Definicja

Mówimy, że funkcja
gdzie
jest przedziałem ograniczonym lub nieograniczonym osi rzeczywistej, jest jednostronnie ciągła na
jeżeli

Każda funkcja jednostronnie ciągła na
jest ciągła w każdym punkcie tego przedziału
. Istnieją funkcje ciągłe, które nie są jednostajnie ciągłe.

Własności funkcji ciągłych na przedziale domkniętym.

Zakładamy, że funkcja
jest ciągła na

1. Funkcja
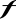
   jest jednostajnie ciągła na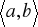
   

2. Funkcja
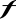
   jest ograniczona na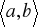
   , tzn.

3. Funkcja
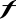
   osiąga swoje kresy, tzn. istnieją takie Punty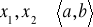
   , że:

4. Jeżeli
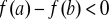
   to istnieje taki punkt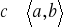
   , że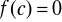
   

5. Twierdzenie o własnościach Darbouxl

Jeżeli funkcja
jest ciągła na przedziale
(niekoniecznie domkniętym) oraz przyjmuje w punktach

dwie różne wartości

to funkcja

w przedziale
przyjmuje wszystkie wartości pośrednie między
,
tj.

Wniosek

Wartości funkcji ciągłej na przedziale domkniętym
wypełnia przedział domknięty

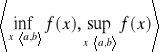
6. Jeżeli funkcja
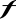
   jest funkcją różnowartościową, ciągłą na przedziale domkniętym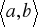
   to funkcja odwrotna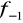
   jest ciągła na przedział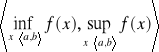
   

Rachunek różniczkowy funkcji rzeczywistej jednej zmiennej.

Pochodna funkcji rzeczywistej zmiennej rzeczywistej:

Niech będzie dana funkcja
dla
przyrostem zmiennej niezależnej

w
nazywamy różnice
a przyrostem zmiennej zależnej w
nazywamy różnicę
przy czym

Iloraz
to tzw. iloraz różnicowy.

Jeżeli przy
istnieje granica właściwa lub niewłaściwa ilorazu różnicowego
funkcji
w
to punktowi
można przyporządkować wyrażenie

Zmieniając
uzyskujemy funkcję
która przyporządkowuje zmienne
wyrażenie

Definicja

Funkcję
gdzie
nazywamy pochodną funkcji
.

We wzorze
można rozważać granice jednostronne.

Definicja

Pochodną lewostronną funkcji
w
nazywamy wyrażenie

Definicja

Pochodną prawostronną funkcji
w
nazywamy wyrażenie

Jeżeli
istnieje i jest skończona, to funkcję
nazywamy różniczkowalną w
.

Twierdzenie 1

Jeżeli funkcja
określona na przedziale
posiada skończoną pochodną

to funkcja
jest ciągła w
.

Dowód

Ponieważ istnieje skończona granica
więc

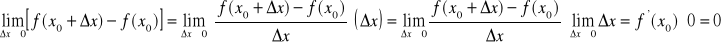
Czyli
otrzymaliśmy, że
jest ciągła w
.

Twierdzenie 2

Jeżeli funkcja
,
posiada skończoną pochodną w
, to:

1. Funkcja
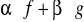
   gdzie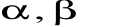
   to funkcja posiada skończoną pochodną w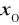
   oraz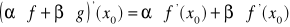
   

2. Iloczyn
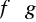
   posiada skończoną pochodną w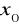
   

3. Przy dodatkowym założeniu
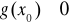
   istnieje pochodna ilorazu

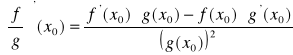
1

---