15.12.2009

Twierdzenie 3 o pochodnej funkcji złożonej

Niech funkcja
będzie różniczkowalna w
oraz niech funkcja
będzie różniczkowalna w
wtedy funkcja złożona
jest różniczkowalna w
oraz

Twierdzenie 4

Jeżeli funkcja
jest ciągła i ściśle monotoniczna (tzn. rosnąca lub malejąca) w pewnym otoczeniu
, oraz istnieje skończona pochodna
to funkcja odwrotna do
posiada pochodną w punkcie
przy czym

Pochodne funkcji elementarnych

c-stała	0

Pochodna funkcji danej w postaci parametrycznej.

Dane są funkcje
,
określone i ciągłe względem parametru
podając związek zmiennej niezależnej
za zmienną zależną
.

Zakładamy, że

1. 
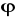
   jest ściśle monotoniczna

2. Istnieje skończona pochodna
   !!!!!!!!

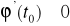
Zatem istnieje funkcja odwrotna
funkcja ta jest ciągła i ściśle monotoniczna

Funkcja złożona
jest ciągła.

Ponieważ

gdzie
więc na podstawie twierdzenia o pochodnej funkcji złożonej otrzymujemy

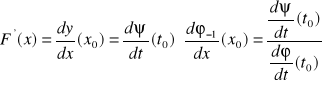
czyli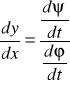

Różniczka.

Dana jest funkcja
ciągła w

Definicja

Mówimy, że funkcja
jest różniczkowalna w
jeżeli jej przyrost w
ma postać

przy czym

stała

Twierdzenie 1

Na to by funkcja
ciągła w
była różniczkowalna w
, potrzeba i wystarcza, by istniała skończona pochodna

Jeżeli warunek ten zachodzi, to

Definicja

Niech funkcja
będzie określona na przedziale
oraz niech istnieje skończona pochodna
dla każdego

Różniczką funkcji
ze względu na przyrost
nazywamy funkcję

Wartość różniczki funkcji
w punkcie
wynosi

Podstawiając

mamy

oraz

czyli

zatem dla dowolnej funkcji
mamy

Ponieważ dla funkcji różniczkowalnej zachodzi równość

Więc dla
bliskich
, otrzymujemy równanie przybliżone

czyli

Podstawiając

czyli

otrzymujemy

dla
bliskich

W szczególności dla
mamy
dla
bliskich
.

4