Wyrównanie sieci

swobodnych

Dla wyrównania sieci liniowo-kątowej potrzebne są
cztery elementy wyjściowe:

-Współrzędne jednego punktu – umiejscowienie sieci

-Azymut jednego boku – orientacja sieci

-Długość jednego boku – skala sieci



d

Brak tych elementów jest charakterystyczny dla
sieci swobodnych

Dla sieci niwelacyjnych niezbędny jest w
klasycznym

wyrównaniu,

przynajmniej

jeden reper. Zdarza się jednak, że stare
repery istniejące od wielu lat nie dorównują
dokładnością najnowszym pomiarom i
włączenie ich do sieci wręcz obniża jej
dokładność.

Jeżeli w konkretnym zadaniu nie jest istotna
wysokość nad poziomem morza, natomiast
ważne są różnice wysokości między
poszczególnymi elementami mierzonego
obiektu – można przeprowadzić wyrównanie
z

odrzuceniem

bezbłędności

punktów

nawiązania.

I metoda wyrównania sieci swobodnych:

Wyrównanie - na przykład sieci niwelacyjnej - można
przeprowadzić

metodą

zawarunkowaną

bez

uwzględniania warunków między reperami.

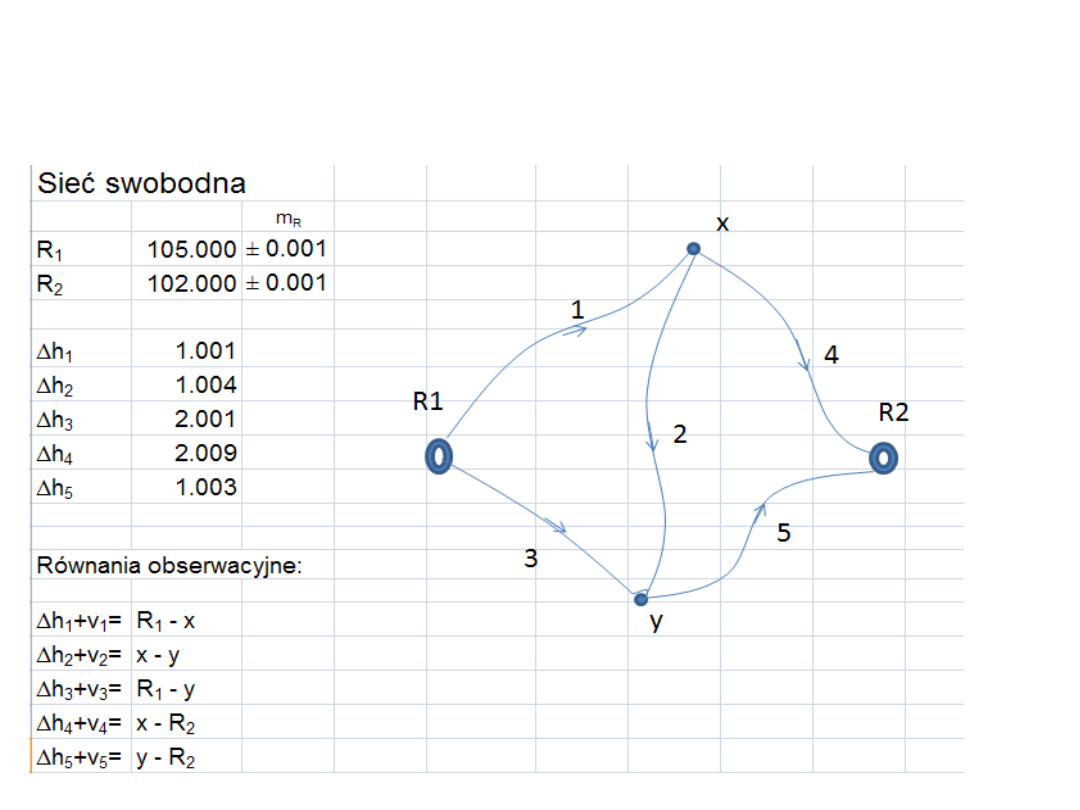
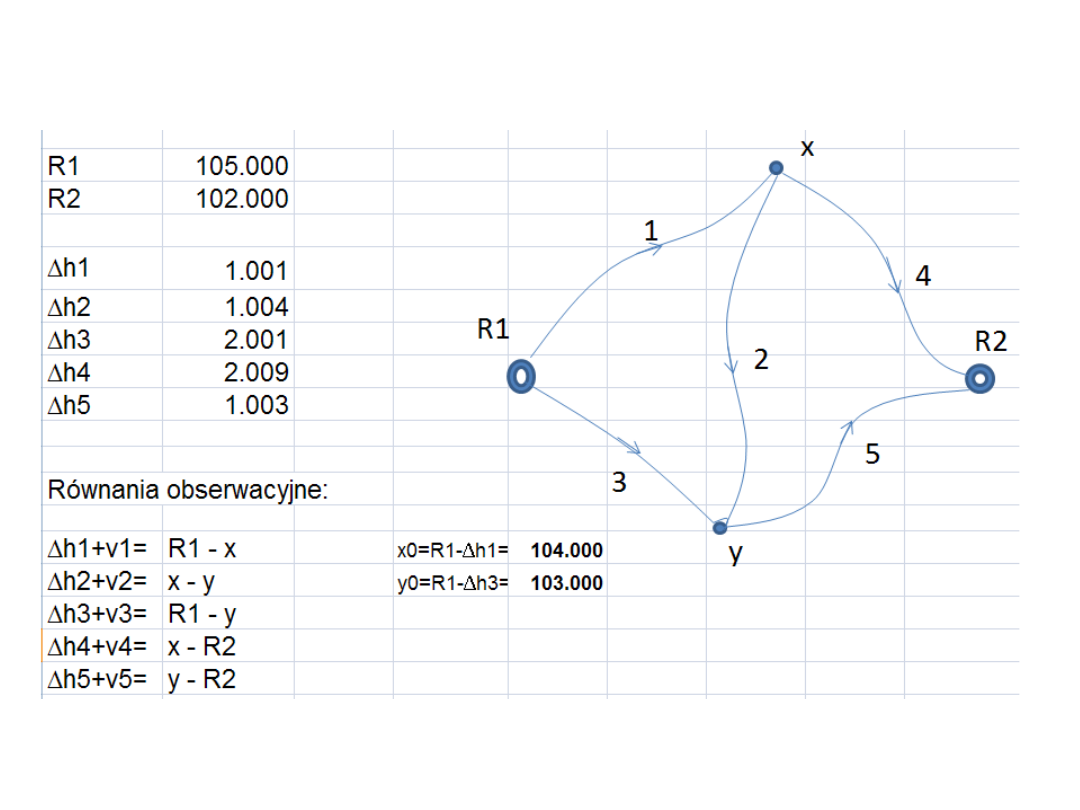
II metoda wyrównania sieci swobodnych:

Układa się równania obserwacyjne jak dla metody
pośredniczącej:

Następnie układa się równania błędów
uwzględniając w nich poprawki do punktów
nawiązania (tu – reperów). Do klasycznych
równań błędów dopisuje się fikcyjne równania
błędów w liczbie równej liczbie współrzędnych
nawiązania. Te fikcyjne równania błędów
otrzymują wagi zależne od średnich błędów
punktów nawiązania.

Metoda ta polega na podziale niewiadomych na te
rozumiane w klasycznym sensie oznaczone jako
x

1

i na punkty nawiązania x

2

które w tym zadaniu

nie są traktowane jako bezbłędne i również
otrzymają poprawki. Wtedy równania błędów
przybierają formę:

L

x

B

x

A

v

2

1







Rozwiązanie tego zadania jest możliwe po
wprowadzeniu obok klasycznego warunku
[vv]=min. drugiego warunku na poprawki dla
punktów nawiązania [xx]=min.

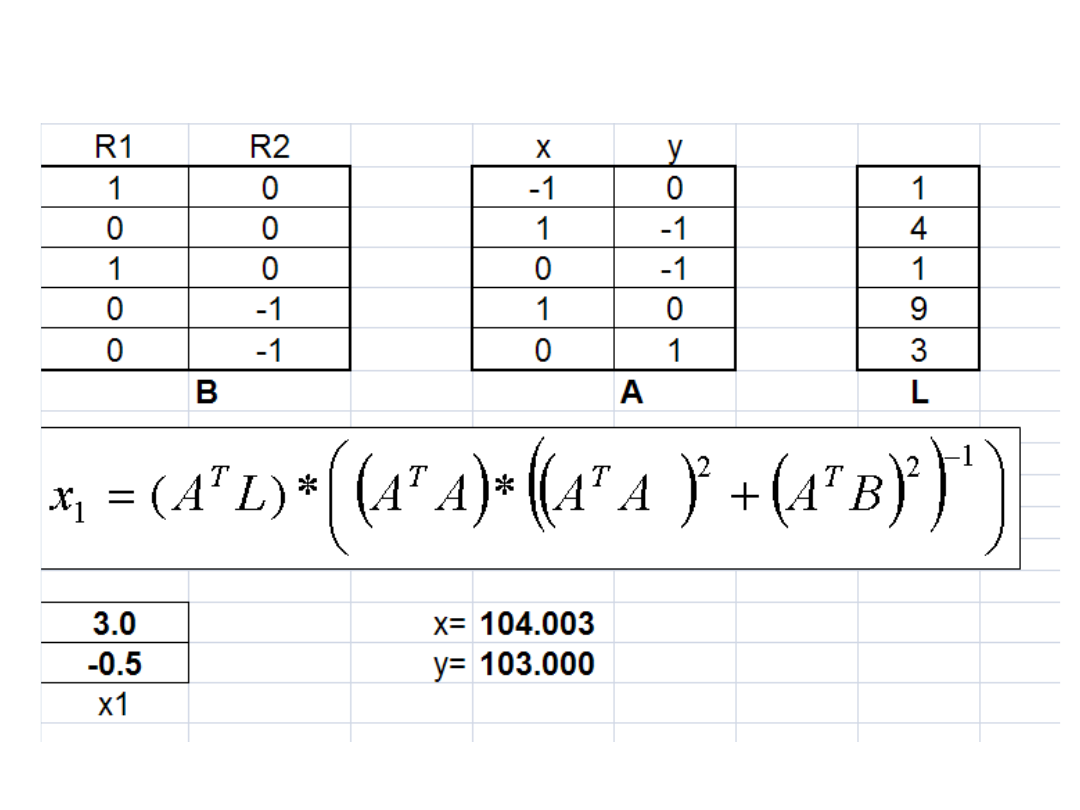
III metoda wyrównania sieci swobodnych:

W oparciu o przedstawione założenia zostały
wyprowadzone następujące wzory na poprawki
niewiadomych:



 

 























 1

2

T

2

T

T

T

1

B

A

A

A

A

A

L)

(A

x



 

 























 1

2

T

2

T

T

T

2

B

A

A

A

B

A

L)

(A

x

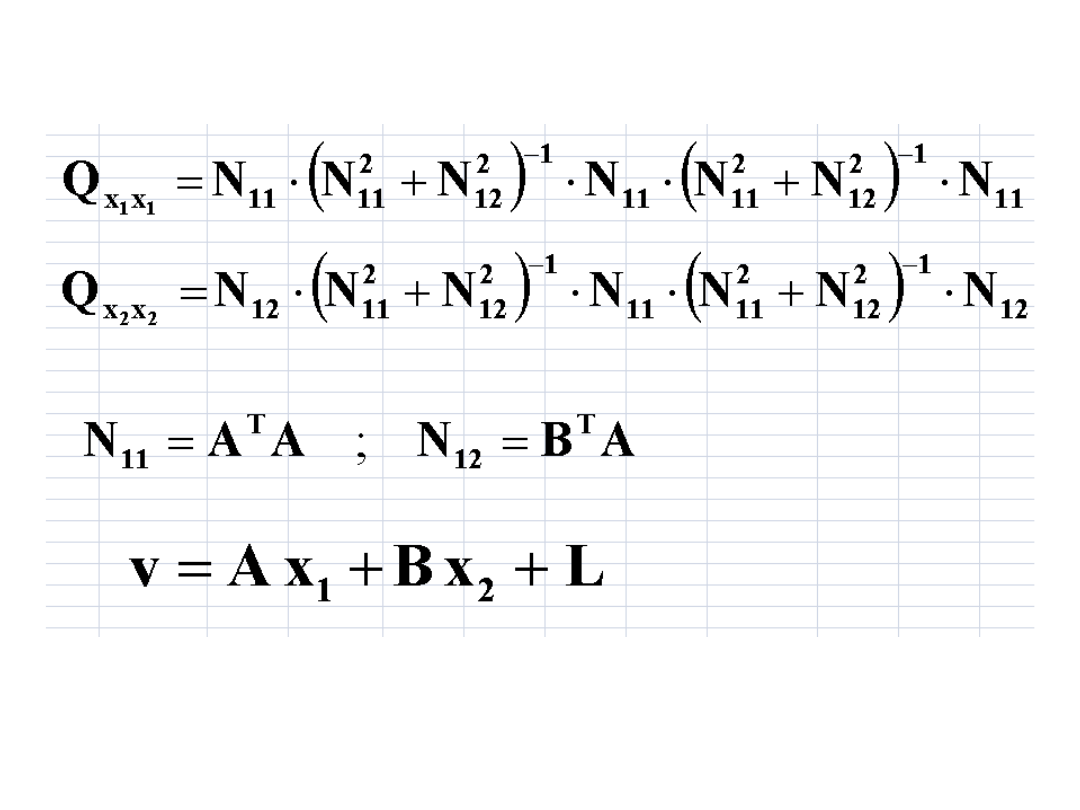
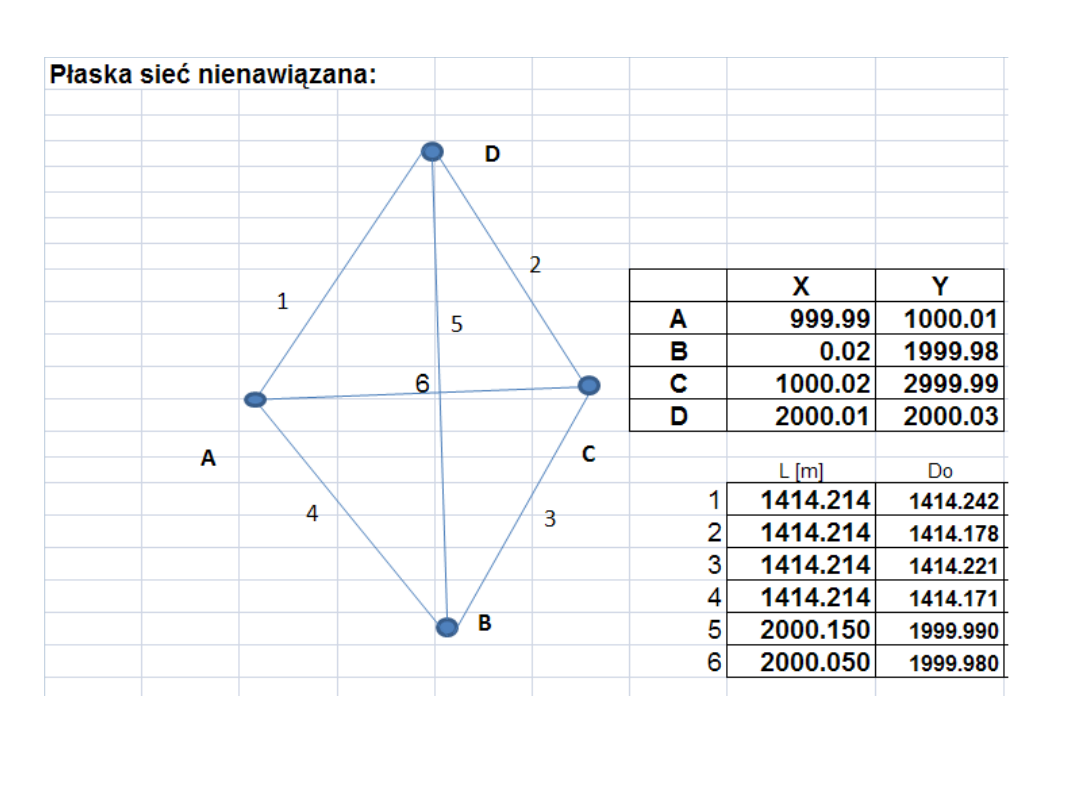
Przy wyrównywaniu sieci kątowo-liniowej bez
nawiązania układa się równania obserwacyjne dla
kątów, kierunków lub długości, a następnie na ich
podstawie macierze A, L i P .
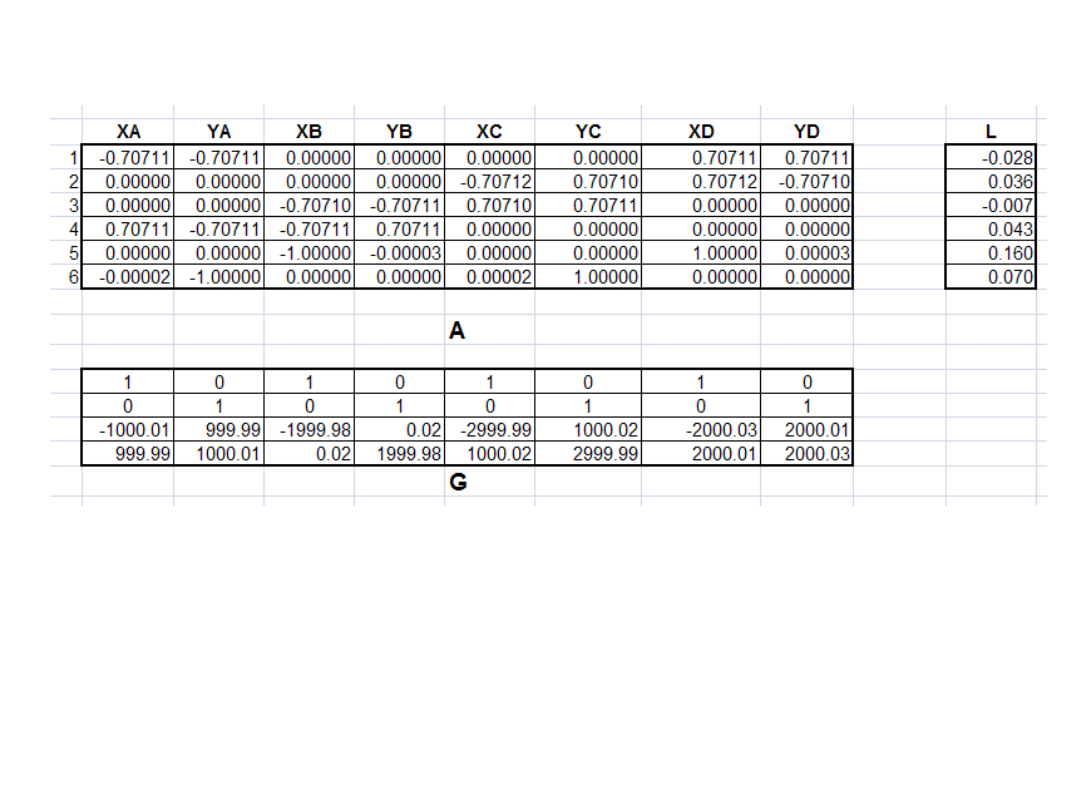
Macierz współczynników równań normalnych oblicza
się jak przy klasycznym wyrównaniu:

N = A

T

. P . A

Dodatkowo układa się macierz G:

































m

m

m

m

x

y

x

y

x

y

y

x

y

x

y

x









2

2

1

1

2

2

1

1

1

0

1

0

1

0

0

1

0

1

0

1

G

IV metoda wyrównania sieci swobodnych:

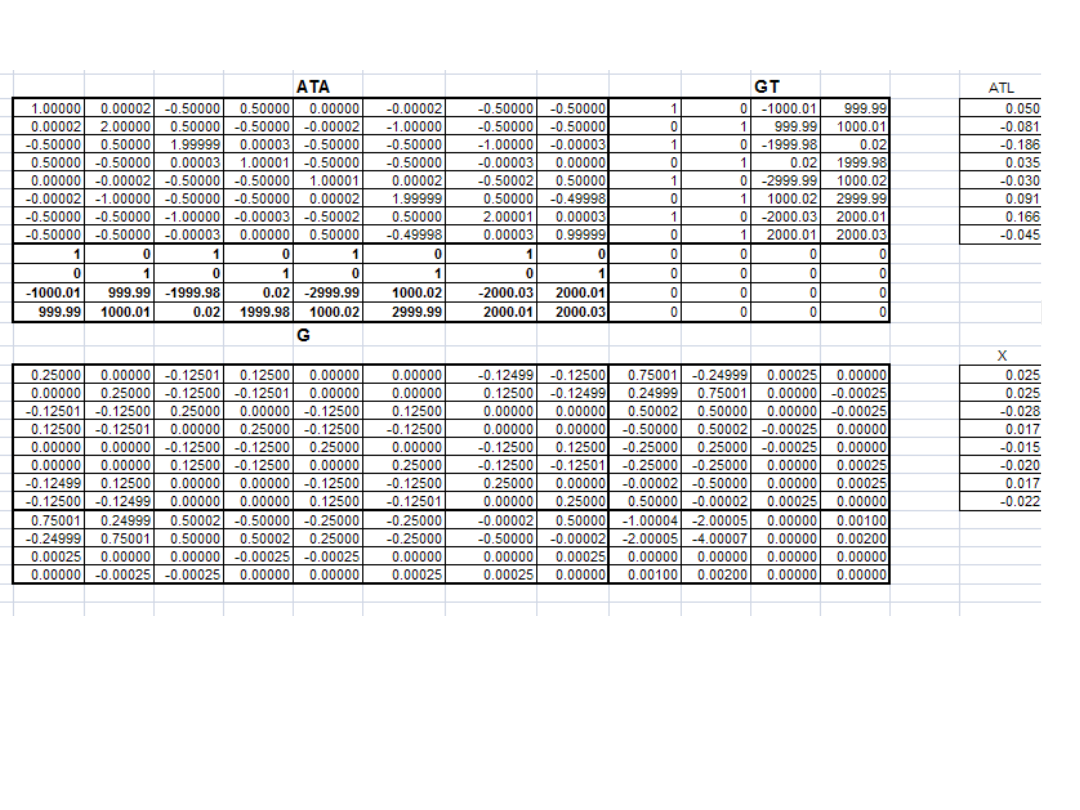
Układa się macierz blokową:













0

G

G

N

T

i oblicza się jej odwrotność:













0

K

K

Q

T

Następnie oblicza się poprawki niewiadomych i
poprawki spostrzeżeń tak jak w klasycznym
wyrównaniu:





L

A

Q

x

T





L

X

A

V







W metodzie IV-tej powstaje bardzo
duża macierz normalna i jej
odwrotność.

To samo zadanie rozwiązywane
metodą III-cią
Wykorzystuje macierze dużo
mniejsze.

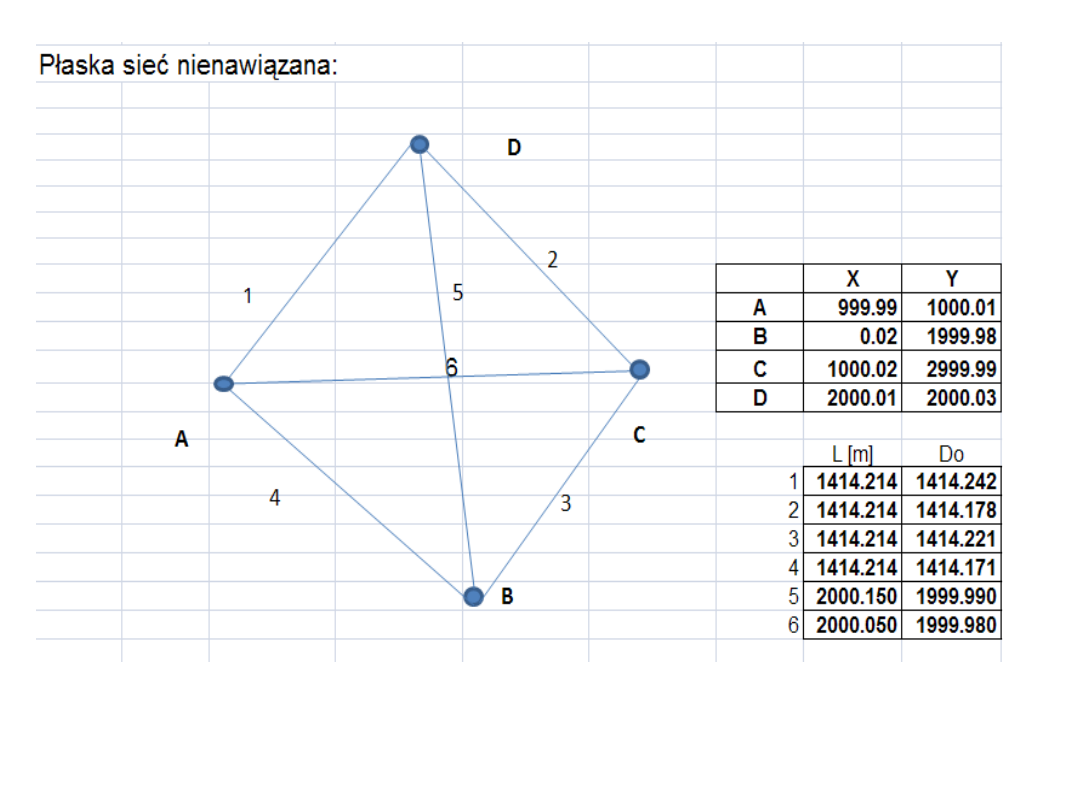
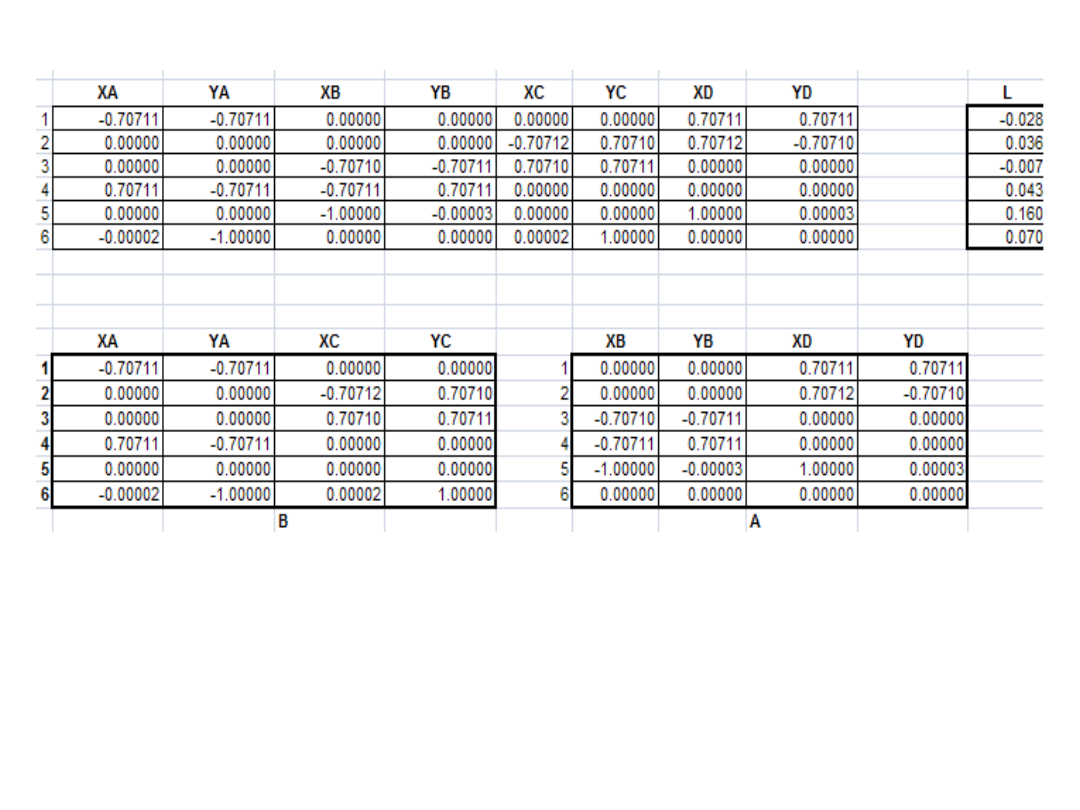
Obliczenie poprawek punktów szukanych:

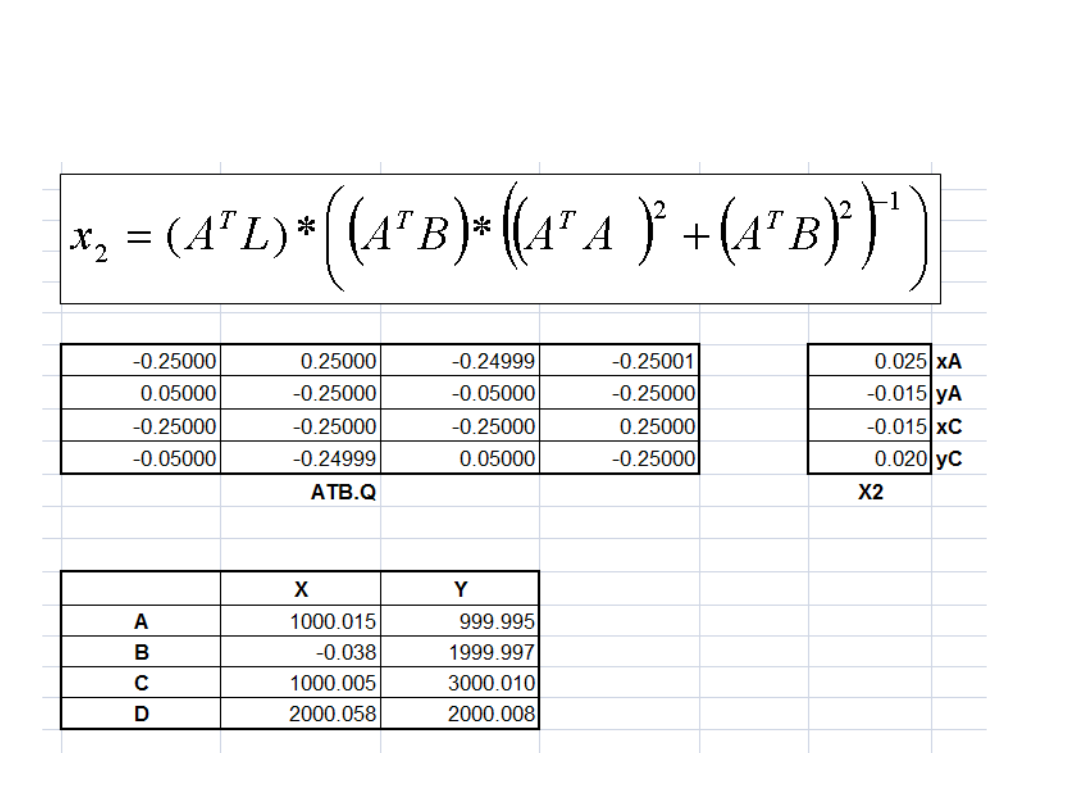
Obliczenie poprawek dla punktów
nawiązania:

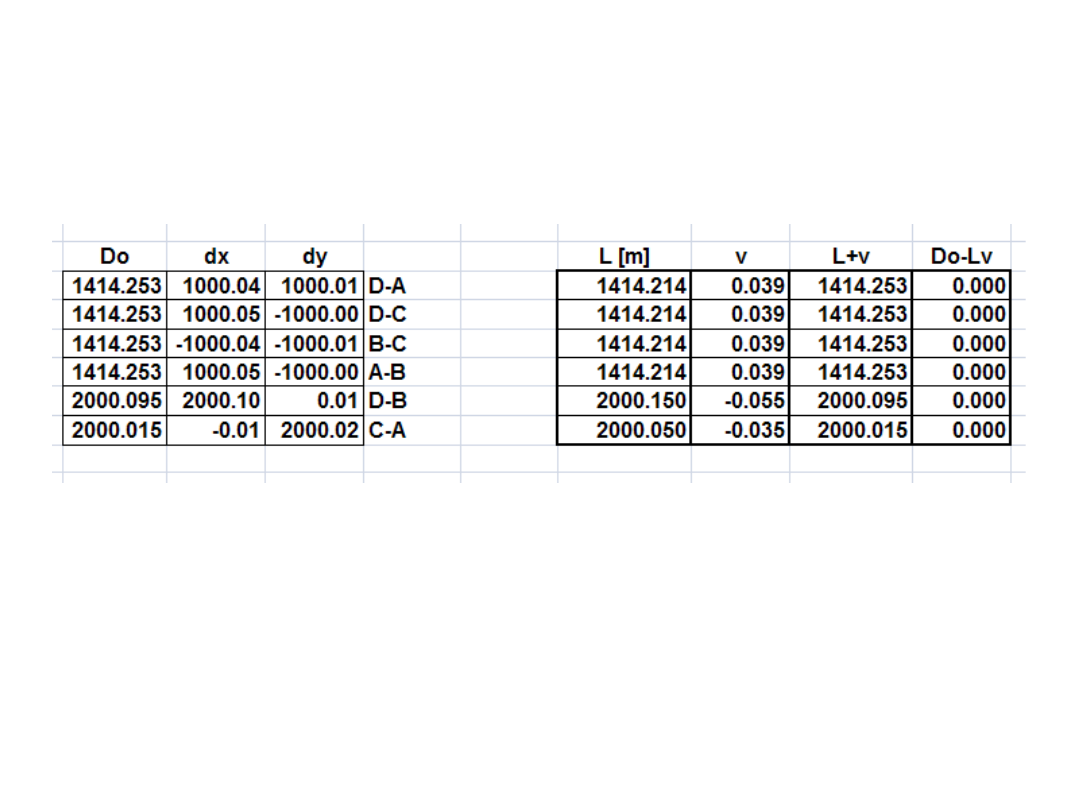
Kontrola generalna: