Elementy fizyki statystycznej

Termodynamika
Gęstości stanów

Funkcje rozkładu

Gaz elektronów

 

Termodynamika

Termodynamika to dział fizyki
zajmujący się energią termiczną
(energią wewnętrzną) układu
Temperatura – podstawowe pojęcie
termodynamiki
Skala Kelvina – bezwzględna skala
temperatury
„odczuwanie temperatury” – zależne
od naszych zmysłów

10

8

10

6

10

4

10

2

10

0

10

-2

10

-9

10

39

T [K]

wszechświat tuż

po powstaniu

najwyższa temp.

uzyskana w lab.
jądro Słońca

powierzchnia Słońca

krzepnięcie wody

wszechświat dziś
wrzenie helu-3

najniższa uzyskana

temperatura

 

Termodynamiczny opis układu

obiekty traktujemy makroskopowo nie wnikając w naturę cząstek z

których się składa
gaz doskonały: cząsteczki gazu traktujemy jako punkty materialne i

zakładamy, że zderzenia z innymi cząstkami i ściankami naczynia są

sprężyste
podstawowe makroskopowe parametry stanu układu to: ciśnienie p,

objętość V i temperatura T
każda zmiana w układzie termodynamicznym (choćby jednego

parametru) nazywa się procesem termodynamicznym
I zasada termodynamiki:

zmiana energii wewnętrznej układu równa jest sumie ilości ciepła i

pracy wymienionej przez układ z otoczeniem

II zasada termodynamiki:

w procesach odwracalnych zachodzących w układzie entropia

pozostaje stała, a w nieodwracalnych wzrasta

 

Pierwsza zasada
termodynamiki

Energia wewnętrzna układu U wzrasta, jeżeli
układ pobiera energię w postaci ciepła Q, i
maleje, kiedy wykonuje pracę W

dla nieznacznej przemiany

W

Q

U

−

=

Δ

Przemiana adiabatyczna
Q = 0

⇒ ΔU = -W

W>0 – praca wykonana

przez układ
W<0 – praca wykonana

nad układem

Rozprężanie swobodne

Q = W = 0

⇒ ΔU = 0

dW

dQ

dU

−

=

 

Przemiany
nieodwracalne

przemiany jednokierunkowe w układzie
zamkniętym nazywamy nieodwracalnymi

o kierunku procesów nieodwracalnych

decyduje zmiana entropii

ΔS układu,

(parametru stanu takiego jak T, p, V)

nie ma zasady zachowania entropii, w

przemianach nieodwracalnych entropia

układu zamkniętego zawsze rośnie

przy nieskończenie małej zmianie stanu układu

∫

=

−

=

Δ

K

P

P

K

T

dQ

S

S

S

T

dQ

dS =

 

Przemiana odwracalna

Przy odwracalnym izotermicznym rozprężaniu gazu

doskonałego zmiana entropii zależy od całkowitego

ciepła dostarczonego ze zbiornika do gazu

Q>0 – przy rozprężaniu entropia gazu rośnie

przy sprężaniu Q<0 (gaz oddaje ciepło) – entropia

gazu maleje lecz entropia zbiornika rośnie

zmiana entropii układu zamkniętego (gaz + zbiornik)

jest sumą obydwu wartości i jest równa zeru

T

Q

S

gaz

−

=

Δ

T

Q

S

zbior

+

=

Δ

0

=

ΔS

T

Q

dQ

T

S

S

S

K

P

P

K

=

=

−

=

Δ

∫

1

0

>

Δ

gaz

S

 

Druga zasada termodynamiki

Entropia układu zamkniętego wzrasta w przemianach
nieodwracalnych i nie zmienia się w przemianach
odwracalnych (entropia nigdy nie maleje)

proces nieodwracalny przebiega w kierunku wzrostu
entropii
wzrost entropii – przejście układu do stanu mniejszego
uporządkowania cząsteczek (stanu większego chaosu)
z I i II zasady termodynamiki wynika:

0

≥

ΔS

dW

TdS

dW

dQ

dU

−

≤

−

=

TdS

dQ ≤

⇒

=

T

dQ

dS

ale

dN

pdV

TdS

dU

μ

+

−

=

zmiany liczby cząstek N w układzie

potencjał chemiczny

dW = pdV

 

Warunki równowagi
termodynamicznej

warunkiem równowagi jest maksimum entropii
lub minimum energii wewnętrznej układu

max

S

S =

V

S

N

U

,

⎟

⎠

⎞

⎜

⎝

⎛

=

∂

∂

μ

Potencjał chemiczny wyraża zmianę energii wewnętrznej układu przy

zmianie liczby jego cząstek o jednostkę w warunkach

stałej entropii i stałej objętości układu

dN

dN

2

1

μ

=

μ

Warunkiem równowagi takiego układu jest równość potencjałów

chemicznych obu układów gazów

Rozpatrzmy układ dwóch gazów o potencjałach chemicznych

μ

1

i

μ

2

w których następuje wymiana

dN

cząstek

 

Pojęcie gazu doskonałego

gaz składa się z cząsteczek, które możemy traktować jako
punkty materialne o tej samej masie
cząsteczki poruszają się chaotycznie i podlegają zasadą
dynamiki Newtona
całkowita liczba cząstek jest bardzo duża
objętość cząstek gazu jest dużo mniejsza od objętości
naczynia
poza momentem zderzenia cząstki nie oddziaływają ze
sobą żadnymi siłami
zderzenia są sprężyste, a czas ich trwania krótki

 

Kinetyczna teoria gazów 1

Rozpatrzmy N cząstek gazu w pudełku o objętości V. Jedna cząstka

odbijająca się sprężyście od lewej ścianki naczynia wywiera nań siłę:

t

p

F

x

Δ

Δ

=

1

x

x

x

x

mv

mv

mv

p

2

=

−

−

=

Δ

)

(

Ponieważ czas pomiędzy kolejnymi zderzeniami z ta samą ścianką wynosi:

L

mv

F

v

L

t

x

x

2

1

2

=

⇒

=

Δ

Dla N cząstek całkowita średnia siła wynosi:

2

2

2

x

x

x

v

Nm

pV

V

v

m

N

S

F

p

L

v

m

N

F

=

⇒

=

=

⇒

=

2

2

2

2

2

3

x

z

y

x

v

v

v

v

v

=

+

+

=

k

E

N

v

Nm

pV

3

2

3

2

=

=

x

y

L

v

x

-v

x

bo cząsteczki zderzają się jednakowo ze wszystkimi

ściankami

iloczyn pV jest stały jak długo stała jest E

K

cząsteczek

2

2

2

z

y

x

v

v

v

=

=

3

2

2

v

v

x

=

⇒

 

Kinetyczna teoria gazów 2

k

E

N

v

Nm

pV

3

2

3

2

=

=

NkT

pV

kT

E

k

=

⇒

=

2

3

równanie stanu

gazu doskonałego

nRT

pV

nR

Nk

=

⇒

=

k – stała Boltzmana

n – liczba moli

N – liczba cząsteczek

R – stała gazowa

trzy stopnie swobody – trzy współrzędne x,y,z

Zasada ekwipatrycji energii – równomierny podział energii na wszystkie stopnie

swobody cząsteczek (½kT na cząsteczkę)

mierząc temperaturę gazu wyznaczmy jednocześnie śr. energię kinetyczną ruchu

postępowego jego cząsteczek

Kinetyczna teoria gazów wiąże właściwości

makroskopowe gazu (np. ciśnienie i temp.) z

właściwościami mikroskopowymi cząsteczek

gazu (np. ich prędkością)

przemiany: izotermiczna,

izochoryczna

, izobaryczna, adiabatyczna

T=const.

V=const.

p=const. Q=0

 

Statystyczny opis układu

makroskopowe właściwości gazów można opisać

odwołując się do zjawisk mikroskopowych
stan każdej cząstki opisujemy przez (x,y,z,p

x

,p

y

,p

z

)

szukamy prawdopodobieństwa zajścia danego

zdarzenia
osobliwością statystycznych prawidłowości jest ich

probabilistyczny charakter
rozkład cząstek w zależności od ich energii opisuje

statystyczna funkcja rozkładu
ze znajomości funkcji rozkładu wyznaczmy

wartości średnie energii, pędu, prędkości cząstek

 

Mikro- i makro-stany

Konfiguracja

W

liczba mikrostanów

Entropia

(10

-23

J/K)

n

1

n

2

I

6

0

6!/(6!· 0!)=1

0

II

5

1

6!/(5!· 1!)=6

2,47

III

4

2

6!/(4!· 2!)=15

3,74

IV

3

3

6!/(3!· 3!)=20

4,13

V

2

4

6!/(2!· 4!)=15

3,74

Rozważmy układ złożony z N = 6 identycznych (ale ponumerowanych)

cząstek w dwóch stanach (np. połówkach zbiornika)

mikrostan: stan zawierający określone cząstki w komórkach przestrzeni fazowej;

makrostan: stan zawierający określoną liczbę cząstek w komórkach przestrzeni fazowej

Stan III

7 makrostanów i 64 mikrostany

wielokrotność konfiguracji -

)

!

!

/(

!

2

1

n

n

N

W

⋅

=

W

k

S

ln

=

wzór Boltzmanna

Konfiguracja IV jest

najbardziej prawdopodobna
P

IV

=20/64=31,3%; ale

P

I

=1/64=1,6% ??

Jeśli w zbiorniku będzie 100

cząstek to W(50,50)=10

29

i

W(100,0)=1, tym bardziej

dla mola cząsteczek N=10

24

 

Przestrzeń fazowa

przestrzeń fazowa jest to 6N wymiarowa przestrzeń o osiach

współrzędnych x,y,z,p

x

,p

y

,p

z

każdy punkt przestrzeni fazowej jednoznacznie określa

mikrostan cząstki, tzn. podaje jej położenie i pęd
sekwencja mikrostanów, które przyjmował układ w czasie

tworzy pewną krzywą zwaną trajektorią fazową
dla ruchu jednowymiarowego

stan cząstki określa x, p

x

badania trajektorii fazowej

pozwalają znaleźć jego

podstawowe własności

dynamiczne

x

p

x

t

1

t

2

 

Układy zwyrodniałe i
niezwyrodniałe

Na N jednakowych cząstek przypada G różnych stanów
N/G << 1 , to cząstki spotykają się rzadko, właściwości

kwantowe nie ujawniają się - układ jest niezwyrodniały
gdy liczba stanów jest tego samego rzędu co cząstek N/G >1,

to układ nazywamy zwyrodniałym
obiekty klasyczne tworzą tylko układy niezwyrodniałe
obiekty kwantowe zazwyczaj tworzą układy zwyrodniałe,

choć w pewnych warunkach mogą być niezwyrodniałe np.

półprzewodniki
rozróżniamy dwa rodzaje cząstek kwantowych:

„

fermiony - o spinie połówkowym podlegają zakazowi Pauliego, dążą

do „samotności”

„

bozony - o spinie całkowitym dążą do „łączenia się”, nieograniczenie

mogą zapełniać ten sam stan

 

Statystyczna funkcja rozkładu

statystyczna funkcja rozkładu dla cząstek o temperaturze T i
potencjale chemicznym

μ określa średnią ilość cząstek

przypadającą na jeden stan układu o energii E
dla gazu niezwyrodniałego stosuje się statystyką klasyczną
(rozkład Maxwella-Boltzmanna)

fizyka statystyczna, która bada właściwości układów
zwyrodniałych, nazywa się statystyką kwantową

„

statystyka Bosego-Einsteina

„

statystyka Fermiego-Diraca

( )

(

)

kT

E

MB

Ne

kT

E

E

f

−

=

⎥⎦

⎤

⎢⎣

⎡

μ

−

−

= exp

( )

(

)

1

1

+

⎥⎦

⎤

⎢⎣

⎡

μ

−

=

kT

E

E

f

FD

exp

( )

(

)

1

1

−

⎥⎦

⎤

⎢⎣

⎡

μ

−

=

kT

E

E

f

BE

exp

 

Statystyki

W dostatecznie dużych temperaturach funkcje rozkładu Fermiego-

Diraca i Bosego-Einsteina przechodzą w klasyczną funkcję Maxwella-

Boltzmanna, układy zwyrodniałe przechodzą w niezwyrodaniałe

FD

(

)

1

>>

⎥⎦

⎤

⎢⎣

⎡

μ

−

kT

E

exp

Dla

( )

(

)

(

)

kT

E

Ne

kT

E

kT

E

E

f

−

=

⎥⎦

⎤

⎢⎣

⎡

μ

−

−

=

±

⎥⎦

⎤

⎢⎣

⎡

μ

−

=

exp

exp

1

1

E

μ

f(E)

MB

-

μ

BE

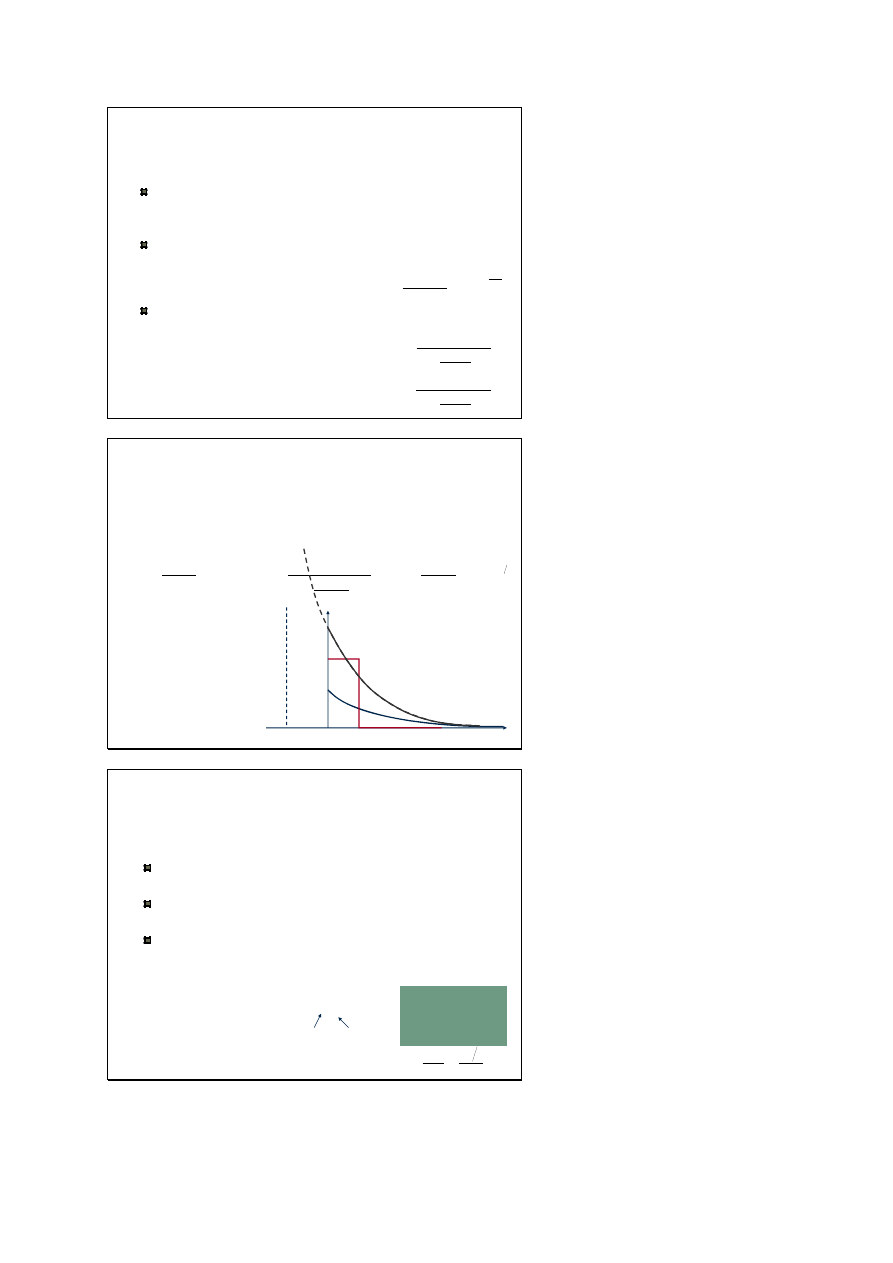
Dla rozkładu Bosego-Einsteina

potencjał chemiczny jest

zawsze ujemny

0

1

Im większa energia tym

mniejsze prawdopodobieństwo

obsadzenia danego stanu

 

Gaz elektronów swobodnych

elektrony swobodne w metalu spełniają warunki gazu
doskonałego
elektrony są fermionami (s=1/2) więc stosujemy statystykę
Fermiego-Diraca
przestrzeń fazowa obiektów kwantowo-mechanicznych
jest skwantowana, a elementarna komórka fazowa zgodnie
z zasada nieoznaczoności Heisenberga ma objętość

3

h

d

d

dp

dp

dxdydzdp

d

p

V

z

y

x

=

Γ

Γ

=

=

Γ

przestrzeń koordynacyjna i pędu

w komórce tej

mogą znajdować

się dwa elektrony o

różnych spinach

Jeśli elektron porusza się swobodnie w objętości V

to jego pęd jest określony z dokładnością do

V

h

d

d

d

V

p

2

3

=

Γ

Γ

=

Γ

V

d

V

=

Γ

 

G(E

0

)

całkowita

liczba stanów

o energii E

0

Funkcja gęstości stanów

V

h

d

p

2

3

=

Γ

( )

dp

h

V

p

dp

p

g

3

2

8

π

=

Funkcję

g(p)

nazywamy gęstości stanów w przestrzeni pędów – liczba komórek

elementarnych (liczba stanów) w objętości

V

w jednostkowym przedziale pędów

m

p

E

2

2

=

mE

p

2

2

=

dE

E

m

dp

2

2

1

=

( )

( )

dE

E

h

m

V

dE

E

g

2

1

3

2

3

2

4

π

=

( )

( )

2

1

3

2

3

2

4

/

E

h

m

V

E

g

π

=

Obliczmy liczbę elementarnych komórek
fazowych o pędach z przedziału p, p + dp

Przechodząc do przestrzeni energii:

gęstość stanów w

przestrzeni energii:

p

p+dp

dp

p

x

p

y

p

z

V

h

dp

p

d

dp

p

p

3

2

2

8

4

π

π

=

Γ

=

objętość sfery
objętość stanu

g(E)

0

E

E

0

 

Kryterium zwyrodnienia

N/G << 1

Obliczmy liczbę stanów cząstek gazu doskonałego

(elektronów) o energii E = (3/2)kT

( )

( )

2

3

3

2

3

0

3

2

2

4

E

h

m

V

dE

E

g

E

G

E

π

=

=

∫

)

(

( )

( )

2

3

2

1

3

2

3

2

3

2

4

kT

h

m

V

E

G

⎟

⎠

⎞

⎜

⎝

⎛

π

=

)

(

( )

( )

1

2

2

1

2

3

2

4

2

3

2

2

3

2

1

2

3

3

<<

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

π

=

⎟

⎠

⎞

⎜

⎝

⎛

π

=

mkT

h

V

N

kT

m

V

h

N

G

N

Azot w warunkach normalnych:

n

=10

25

m

–3

,

m

=10

–26

kg, to N/G=10

-6

<<1

Dla elektronów o koncentracji

n=N/V=

10

28

m

-3

i

m

=10

-30

kg powyższy

warunek jest spełniony dla temperatury przekraczającej 10 000 C

W takich temperaturach metale nie mogą istnieć w stanie stałym, więc

gaz elektronowy w metalach jest zawsze zwyrodniały – opisywany jest

statystyką Fermiego-Diraca

 

Całkowita funkcja rozkładu

Całkowita funkcja rozkładu N

μ,T

(E) jest to funkcja określająca ilość

cząstek obsadzających stany o energii E w całym układzie o

temperaturze T i potencjale chemicznym

μ

( )

)

(

)

(

,

,

E

f

E

g

E

N

T

T

μ

μ

⋅

=

Całkowita ilość cząstek w całym układzie określa się wzorem:

( )

dE

E

f

E

g

dE

E

N

N

T

T

o

∫

∫

∞

μ

∞

μ

⋅

=

=

0

0

)

(

)

(

,

,

Znajomość całkowitej funkcji rozkładu pozwala nam określić średnią

wartość energii lub prędkości cząsteczek – uśrednianie statystyczne

czastek

sumę

energii

suma

dE

E

N

dE

E

N

E

E

=

⋅

=

∫

∫

∞

∞

0

0

)

(

)

(

0

0

N

dv

v

N

v

v

∫

∞

⋅

=

)

(

 

Gaz elektronowy w T = 0 K

Dla elektronów swobodny metal jest swego rodzaju jamą

potencjału. Zgodnie z zasadą Pauliego w temperaturze 0 K

elektrony zajmują kolejno wszystkie stany od najniższego do

ostatniego obsadzonego, który nazywamy poziomem Fermiego,

a odpowiadającą mu energię – energią Fermiego (E

F

)

Analizując funkcję rozkładu Fermiego-Diraca w T = 0 K otrzymujemy:

( )

(

)

=

+

⎥⎦

⎤

⎢⎣

⎡

⋅

μ

−

=

1

0

1

k

E

E

f

FD

exp

1

1

1

=

+

∞

−

e

0

1

1

=

+

∞

+

e

gdy E <

μ

gdy E >

μ

ten sam rezultat przy założeniu

μ = E

F

(obie wielkości są liczone

względem dna jamy potencjału). Dla E = E

F

f(E) = 1/2

Poziom Fermiego jest poziomem o prawdopodobieństwie obsadzenia = 1/2

E

F

 

Położenie E

F

w funkcji T

( )

1

2

1

<

< E

f

( )

2

1

=

E

f

( )

2

1

0

<

< E

f

dla E < E

F

dla E = E

F

dla E > E

F

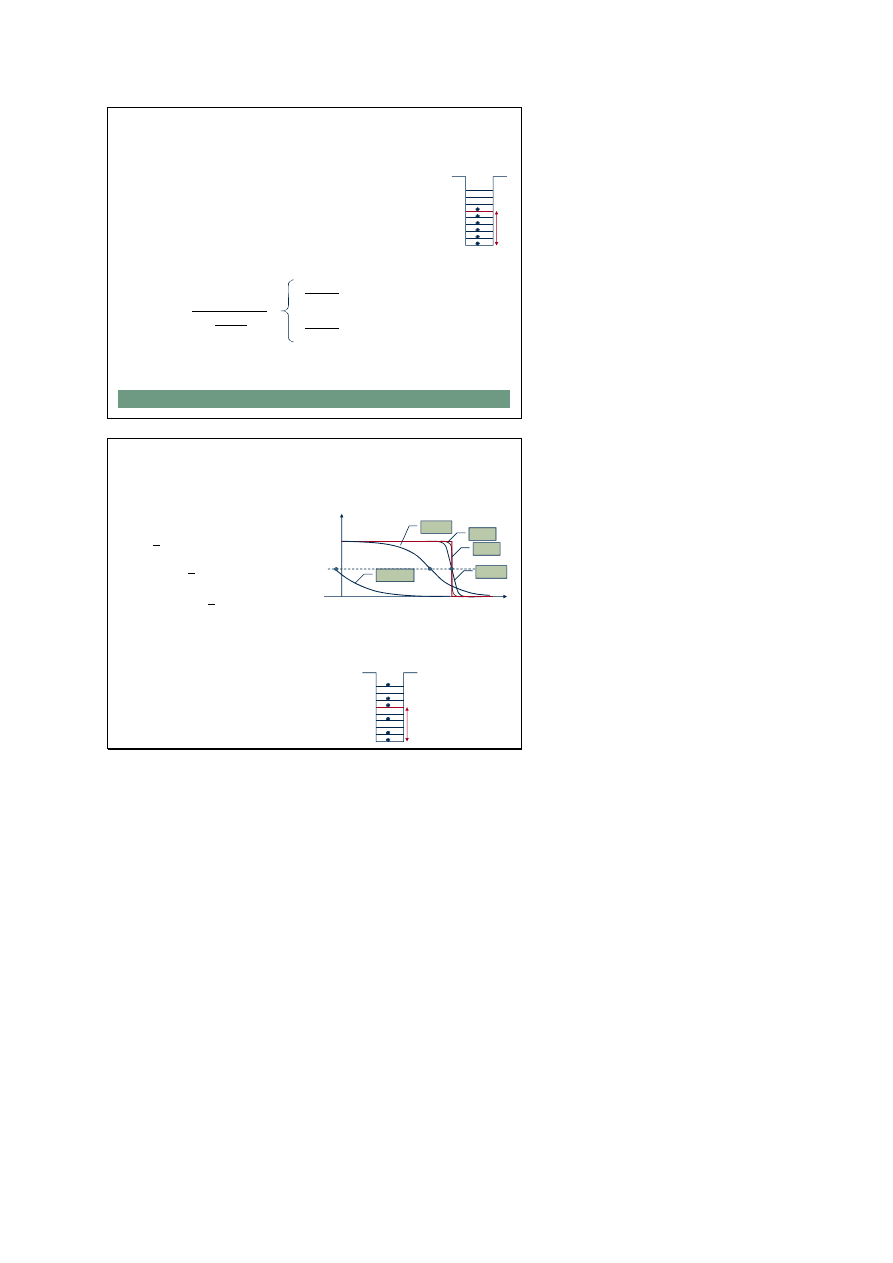
Ze wzrostem temperatury poziom Fermiego nieznacznie się

obniża a funkcja rozkładu staje się coraz bardziej wygładzona,

część elektronów przechodzi na wyższe poziomy energetyczne

E

F

Jak pamiętamy dla bardzo

wysokich temperatur rozkład

FD przechodzi w rozkład MB

f(E)

E

E

0

F

T=0

300

1000

2000

10 000

1

½

0