Podstawy logiki i teorii mnogości Ćwiczenie 3
---------------------------------------------------------------------------------------------------------------------------------------
– 1 –
ĆWICZENIE 3
Klasyczny Rachunek Zdań (KRZ): literał, alternatywa elementarna, koniunkcja
elementarna, formuła w koniunkcyjnej postaci normalnej, formuła w alternatywnej postaci
normalnej, minimalna apn i kpn, siatka karnaugha.
Postacie normalne formuł KRZ
DEF
Formuły p i
p
¬
¬
¬
¬
, gdzie p jest dowolną zmienną zdaniową, nazywamy
literałami
:
p
jest
literałem pozytywnym
, a
p
¬
¬
¬
¬
negatywnym
. Literały
p
i
p
¬
¬
¬
¬
są
przeciwne
(jeden względem
drugiego).
Alternatywa elementarna (klauzula)
jest to alternatywa skończenie wielu literałów, np.
r
q
p
∨∨∨∨
¬
¬
¬
¬
∨∨∨∨
.
Koniunkcja elementarna
jest to koniunkcja skończenie wielu literałów, np.
r
q
p
∧∧∧∧
¬
¬
¬
¬
∧∧∧∧
.
Formuła w koniunkcyjnej postaci normalnej
(kpn
)
jest to koniunkcja skończenie wielu
alternatyw elementarnych, np.
((((
)))) ((((
))))
r
p
r
q
p
¬
¬
¬
¬
∨∨∨∨
¬
¬
¬
¬
∧∧∧∧
∨∨∨∨
¬
¬
¬
¬
∨∨∨∨
Formuła w alternatywnej postaci normalnej
(apn)
jest to alternatywa skończenie wielu
koniunkcji elementarnych, np.
((((
)))) ((((
))))
r
p
r
q
p
¬
¬
¬
¬
∧∧∧∧
¬
¬
¬
¬
∨∨∨∨
∧∧∧∧
¬
¬
¬
¬
∧∧∧∧
TW. Każda formuła KRZ jest logicznie równoważna pewnej formule w kpn i pewnej
formule w apn.
Przypadki szczególne:
(1)
(((( ))))
0
=
==
=
A
w
dla każdego wartościowania w.
Wtedy
A
jest logicznie równoważna formule
p
p
¬
¬
¬
¬
∧∧∧∧
, która jest w apn
(2)
(((( ))))
1
=
==
=
A
w
dla każdego wartościowania w.
Wtedy
A
jest logicznie równoważna formule
p
p
¬
¬
¬
¬
∨∨∨∨
, która jest w kpn
Podstawy logiki i teorii mnogości Ćwiczenie 3
---------------------------------------------------------------------------------------------------------------------------------------
– 2 –
TW. Formuła w kpn jest tautologią KRZ wtedy i tylko wtedy, gdy w każdej składowej
alternatywie elementarnej występuje para przeciwnych literałów.
TW. Formuła w apn nie jest spełnialna wtedy i tylko wtedy, gdy w każdej składowej
koniunkcji elementarnej występuje para przeciwnych literałów.
Sprowadzanie formuł KRZ do apn i kpn metodą przekształceń równoważnych
Podformuły danej formuły zastępujemy formułami równoważnymi w następującej kolejności:
(1) eliminujemy spójniki ↔ i → zastępując odpowiednio:
C
D
↔
przez
(
) (
)
C
D
D
C
→
∧
→
C
D
→
przez
(
)
¬ ∨
C
D
(2) wprowadzamy znak negacji do wnętrza oraz usuwamy
podwójną negację zastępując odpowiednio:
(
)
k
C
C
∧
∧
¬
K
1
przez
(
)
k
C
C
¬
∨
∨
¬
K
1
(
)
k
C
C
∨
∨
¬
K
1
przez
(
)
k
C
C
¬
∧
∧
¬
K
1
¬¬C
przez
C
(3) stosujemy
a) rozdzielczość koniunkcji względem alternatywy (kpn)
zastępując odpowiednio:
(
)
k
C
C
D
∧
∧
∨
K
1
przez
(
)
(
)
k
C
D
C
D
∨
∧
∧
∨
K
1
(
)
D
C
C
k
∨
∧
∧
K
1
przez
(
)
(
)
D
C
D
C
k
∨
∧
∧
∨
K
1
b) rozdzielczość alternatywy względem koniunkcji (apn)
zastępując odpowiednio:
((((
))))
k
C
C
D
∨∨∨∨
∨∨∨∨
∧∧∧∧
K
1
przez
((((
))))
((((
))))
k
C
D
C
D
∧∧∧∧
∨∨∨∨
∨∨∨∨
∧∧∧∧
K
1
((((
))))
D
C
C
k
∧∧∧∧
∨∨∨∨
∨∨∨∨
K
1
przez
((((
))))
((((
))))
D
C
D
C
k
∧∧∧∧
∨∨∨∨
∨∨∨∨
∧∧∧∧
K
1
Podstawy logiki i teorii mnogości Ćwiczenie 3
---------------------------------------------------------------------------------------------------------------------------------------
– 3 –
Sprowadzanie formuł KRZ do apn i kpn metodą tablicową - przykład
r
q
q
p
A
¬
¬
¬
¬
∧
∧
∧
∧
↔
↔
↔
↔
∧
∧
∧
∧
=
=
=
=
p
q
r
q
p
∧∧∧∧
r
¬
¬
¬
¬
r
q
¬
¬
¬
¬
∧∧∧∧
A
apn
kpn
1
1
1
1
0
0
0
r
q
p
¬
¬
¬
¬
∨∨∨∨
¬
¬
¬
¬
∨∨∨∨
¬
¬
¬
¬
1
1
0
1
1
1
1
r
q
p
¬
¬
¬
¬
∧∧∧∧
∧∧∧∧
1
0
1
0
0
0
1
r
q
p
∧∧∧∧
¬
¬
¬
¬
∧∧∧∧
1
0
0
0
1
0
1
r
q
p
¬
¬
¬
¬
∧∧∧∧
¬
¬
¬
¬
∧∧∧∧
0
1
1
0
0
0
1
r
q
p
∧∧∧∧
∧∧∧∧
¬
¬
¬
¬
0
1
0
0
1
1
0
r
q
p
∨∨∨∨
¬
¬
¬
¬
∨∨∨∨
0
0
1
0
0
0
1
r
q
p
∧∧∧∧
¬
¬
¬
¬
∧∧∧∧
¬
¬
¬
¬
0
0
0
0
1
0
1
r
q
p
¬
¬
¬
¬
∧∧∧∧
¬
¬
¬
¬
∧∧∧∧
¬
¬
¬
¬
apn: (
r
q
p
¬
¬
¬
¬
∧∧∧∧
∧∧∧∧
)
∨ (
r
q
p
∧∧∧∧
¬
¬
¬
¬
∧∧∧∧
)
∨ (
r
q
p
¬
¬
¬
¬
∧∧∧∧
¬
¬
¬
¬
∧∧∧∧
)
∨ (
r
q
p
∧∧∧∧
∧∧∧∧
¬
¬
¬
¬
)
∨ (
r
q
p
∧∧∧∧
¬
¬
¬
¬
∧∧∧∧
¬
¬
¬
¬
)
∨
(
r
q
p
¬
¬
¬
¬
∧∧∧∧
¬
¬
¬
¬
∧∧∧∧
¬
¬
¬
¬
)
kpn: (
r
q
p
¬
¬
¬
¬
∨∨∨∨
¬
¬
¬
¬
∨∨∨∨
¬
¬
¬
¬
)
∧ (
r
q
p
∨∨∨∨
¬
¬
¬
¬
∨∨∨∨
)
Minimalizacja formuł apn i kpn.
DEF.
Minimalną apn
formuły A nazywamy apn mającą najmniejszą liczbę literałów spośród wszystkich apn
tej formuły. Podobnie określamy
minimalną kpn
.
Do upraszczania formuł w postaci apn i kpn stosujemy następujące równoważności logiczne:
(
)
p
p
p
∧
↔
p
p
↔
↔
↔
↔
∧
∧
∧
∧ 1
1
1 ↔
↔
↔
↔
∨
∨
∨
∨
p
(
)
p
p
p
∨
↔
0
0 ↔
↔
↔
↔
∧
∧
∧
∧
p
p
p
↔
↔
↔
↔
∨
∨
∨
∨ 0
((((
))))
p
q
p
p
↔
↔
↔
↔
∧
∧
∧
∧
∨
∨
∨
∨
((((
)))) ((((
))))
p
q
p
q
p
↔
↔
↔
↔
¬
¬
¬
¬
∧
∧
∧
∧
∨
∨
∨
∨
∧
∧
∧
∧
((((
))))
p
q
p
p
↔
↔
↔
↔
∨
∨
∨
∨
∧
∧
∧
∧
((((
)))) ((((
))))
p
q
p
q
p
↔
↔
↔
↔
¬
¬
¬
¬
∨
∨
∨
∨
∧
∧
∧
∧
∨
∨
∨
∨
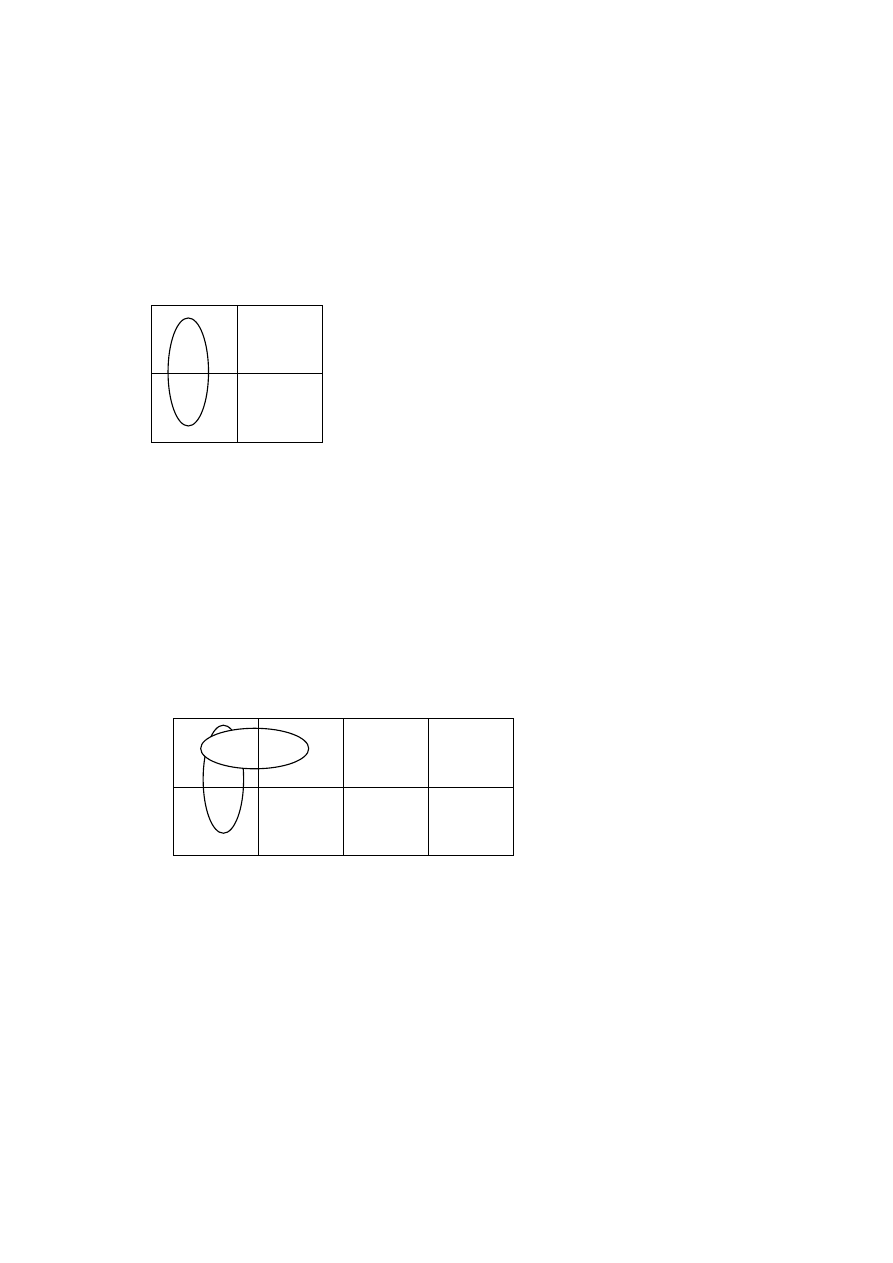
Podstawy logiki i teorii mnogości Ćwiczenie 3
---------------------------------------------------------------------------------------------------------------------------------------
– 4 –
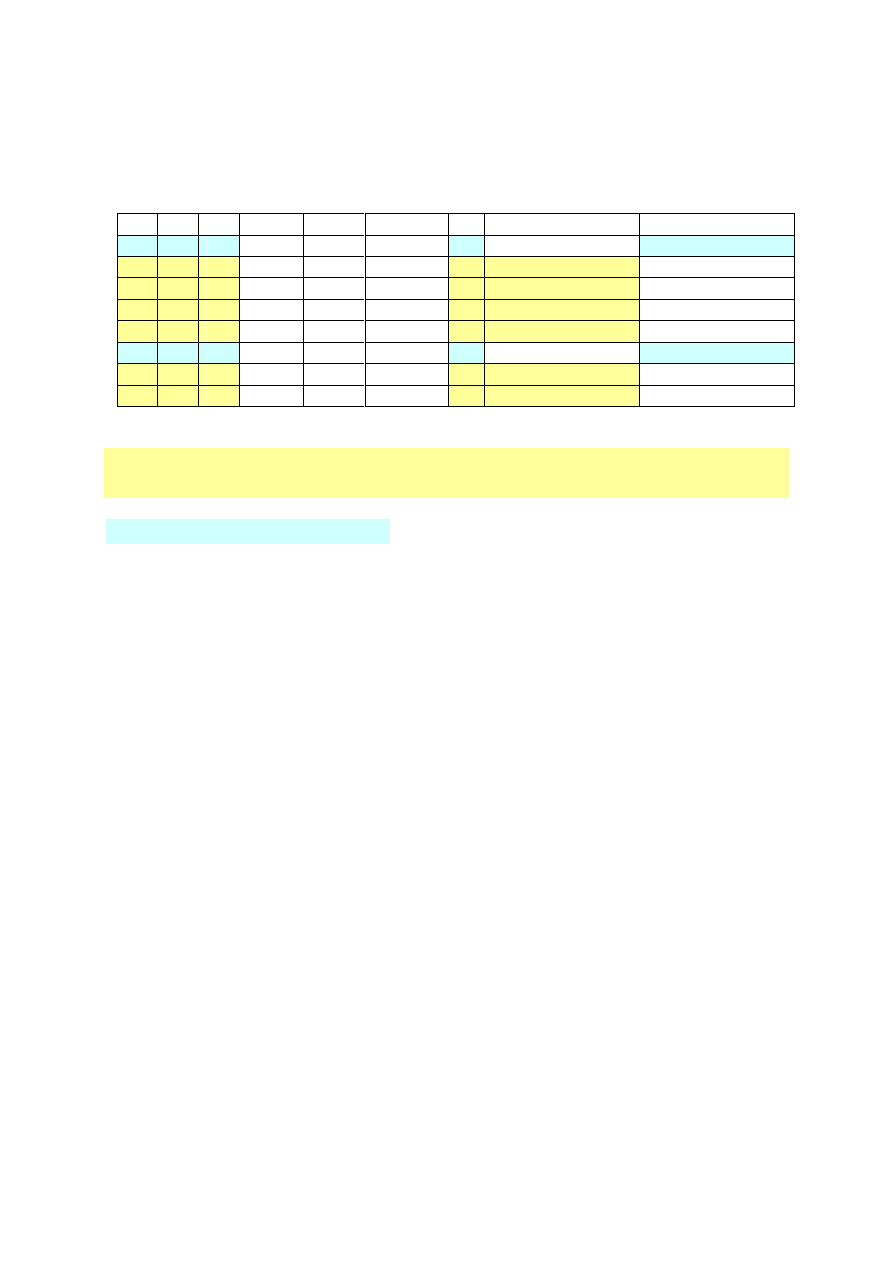
Minimalizacja apn – siatki Karnaugh’a
1) 2 zmienne
((((
)))) ((((
))))
q
q
p
q
p
↔
↔
↔
↔
∧
∧
∧
∧
¬
¬
¬
¬
∨
∨
∨
∨
∧
∧
∧
∧
q
¬
¬
¬
¬q
p
¬
¬
¬
¬p
Zaznaczamy
n
2 sąsiadujących pól (możliwie najwięcej) i redukujemy tą zmienną, dla której
mamy raz jej negację i raz bez negacji. Reszta bez zmian.
2) 3 zmienne
((((
)))) ((((
)))) ((((
)))) ((((
)))) ((((
))))
r
q
r
p
r
q
p
r
q
p
r
q
p
∧
∧
∧
∧
¬
¬
¬
¬
∨
∨
∨
∨
∧
∧
∧
∧
↔
↔
↔
↔
∧
∧
∧
∧
¬
¬
¬
¬
∧
∧
∧
∧
¬
¬
¬
¬
∨
∨
∨
∨
∧
∧
∧
∧
¬
¬
¬
¬
∧
∧
∧
∧
∨
∨
∨
∨
∧
∧
∧
∧
∧
∧
∧
∧
q
¬
¬
¬
¬q ¬
¬
¬
¬q q
p
¬
¬
¬
¬p
r r
¬
¬
¬
¬r ¬
¬
¬
¬r
p
∧∧∧∧q
p
∧∧∧∧¬
¬
¬
¬q
¬
¬
¬
¬p∧∧∧∧q
¬
¬
¬
¬p∧∧∧∧¬
¬
¬
¬q
X
X
X
Podstawy logiki i teorii mnogości Ćwiczenie 3
---------------------------------------------------------------------------------------------------------------------------------------
– 5 –
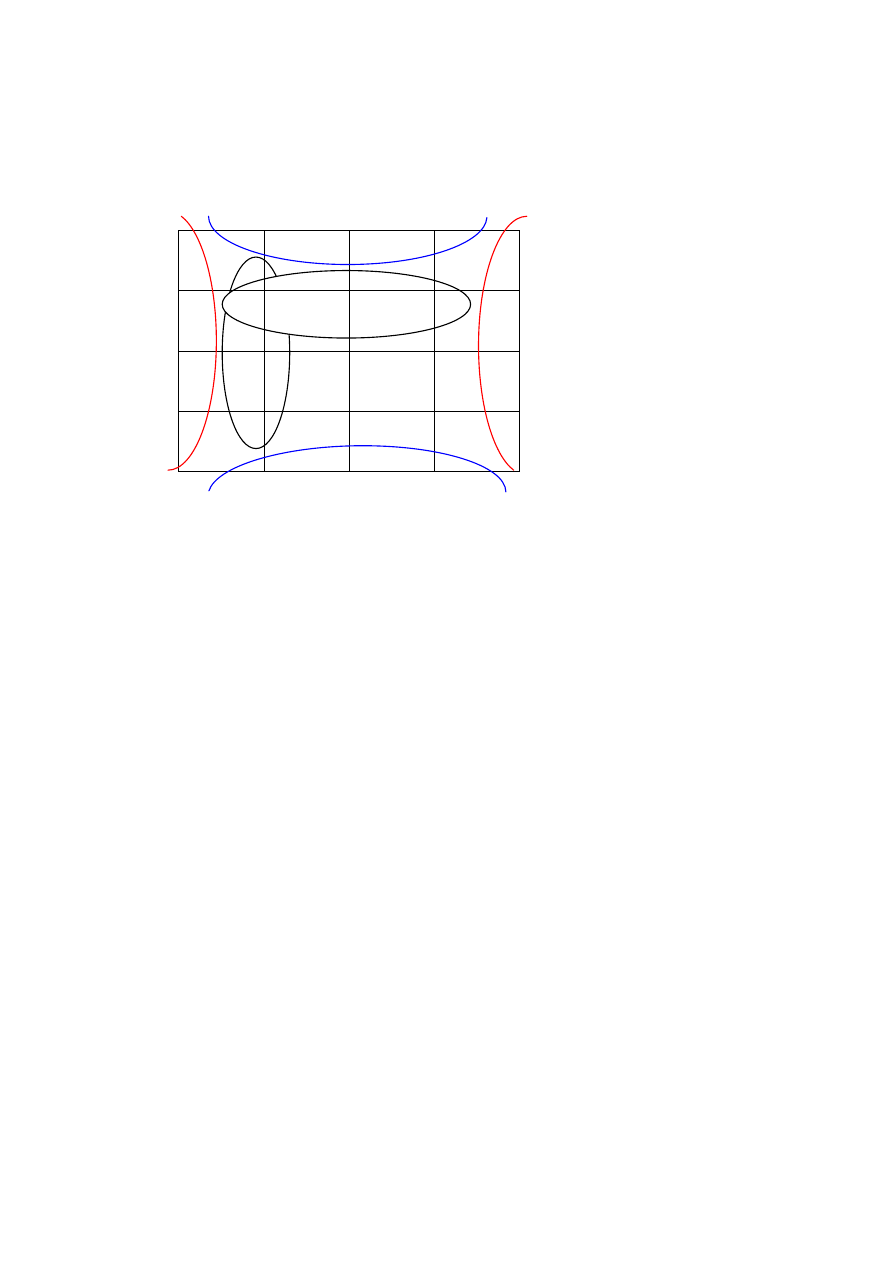
3) 4 zmienne
((((
)))) ((((
)))) ((((
))))
q
p
s
r
s
r
q
p
r
q
p
q
p
p
∨
∨
∨
∨
∨
∨
∨
∨
∨
∨
∨
∨
↔
↔
↔
↔
∧
∧
∧
∧
¬
¬
¬
¬
∧
∧
∧
∧
¬
¬
¬
¬
∧
∧
∧
∧
¬
¬
¬
¬
∨
∨
∨
∨
∧
∧
∧
∧
¬
¬
¬
¬
∧
∧
∧
∧
¬
¬
¬
¬
∨
∨
∨
∨
∧
∧
∧
∧
¬
¬
¬
¬
∨
∨
∨
∨
q q q q
p
¬
¬
¬
¬p
¬
¬
¬
¬p
p
r r
¬
¬
¬
¬r ¬
¬
¬
¬r
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
Podstawy logiki i teorii mnogości Ćwiczenie 3
---------------------------------------------------------------------------------------------------------------------------------------
– 6 –
Ćwiczenie 3: wiadomości i umiejętności
1.
Po ćwiczeniu 3 student powinien znać definicje pojęć podanych w nagłówku ćwiczenia
2.
Student powinien posiadać następujące umiejętności:
•
dla danej formuły KRZ wyznaczyć równoważną apn i kpn metodą przekształceń
równoważnych
•
dla danej formuły KRZ wyznaczyć równoważną apn i kpn metodą tablicową
•
dla danej apn (kpn) znaleźć jej postać minimalną za pomocą siatki Karnaugha