X L V I I I K O N F E R E N C J A N AU K O W A

KOMITETU INŻ YNIERII LĄ DOWEJ I WODNEJ PAN

I KOMITETU NAUKI PZITB

Opole – Krynica

2002

Maciej SZUMIGAŁ A

1

MODEL PRĘ TOWY I PRZESTRZENNY STALOWEGO ELEMENTU

OBETONOWANEGO W ŚWIETLE WYNIKÓW EKSPERYMENTU

1. Wprowadzenie

W krajach Europy Zachodniej, a zwłaszcza w RFN i we Francji stosuje się często stalowe
konstrukcje obetonowane. Podstawowym powodem ich zastosowania są wymagania
przeciwpoż arowe, choć nie jest to jedyna przyczyna obetonowywania konstrukcji stalowych.
Poprzez obetonowanie konstrukcji stalowej moż na ponadto zwiększyć jej nośność,
sztywność i polepszyć stateczność.

W prezentowanym referacie przedstawione zostaną jedynie pewne wybrane aspekty

modelowania statyczno-wytrzymałościowego konstrukcji stalowych obetonowanych.
Zagadnienia ochrony przeciwpoż arowej i przepływó w ciepła były przedmiotem innych
publikacji autora.

Podstawowym, prezentowanym dalej problemem będzie kwestia modelowania

numerycznego stalowych elementó w obetonowanych w świetle własnych badań
eksperymentalnych przeprowadzonych na modelach w duż ej skali technicznej.

2. Opis badań doświadczalnych

Przedmiotem badań eksperymentalnych było sześć słupó w stalowych obetonowanych
o długości 6,0 m. Stalowy rdzeń słupa stanowił spawany dwuteownik szerokostopowy
zaprojektowany indywidualnie, o wymiarach h x b = 240 mm, o zmniejszonych grubościach
pasó w i środnika w stosunku do typowego przekroju typu HKS. Grubości tych elementó w
wynosiły t

f

= 12 mm i t

w

= 5 mm. Słup obetonowano obustronnie, a wspó łpracę betonu i stali

zapewniały strzemiona przyspawane do środnika i pasó w .

Badany słup umieszczono poziomo na podporach jak belkę i obciążano podłuż ną siłą

ściskającą oraz dwiema siłami poprzecznymi do jego osi. Do wywierania obciążenia
poprzecznego zastosowano układ dźwigniowy (rys. 1), któ ry w prosty sposó b umoż liwiał
nadawanie przemieszczeń (sterowanie przemieszczeniem). Cykl pomiarowy polegał na
wstępnym przyłoż eniu siły ściskającej element, a pó źniej poprzez dźwignię nadawano
przemieszczenia prostopadłe do osi badanego słupa, a ich wielkość odpowiadała przyrostowi
siły ró wnemu 20 kN.

1

Dr inż ., Instytut Konstrukcji Budowlanych Politechniki Poznańskiej

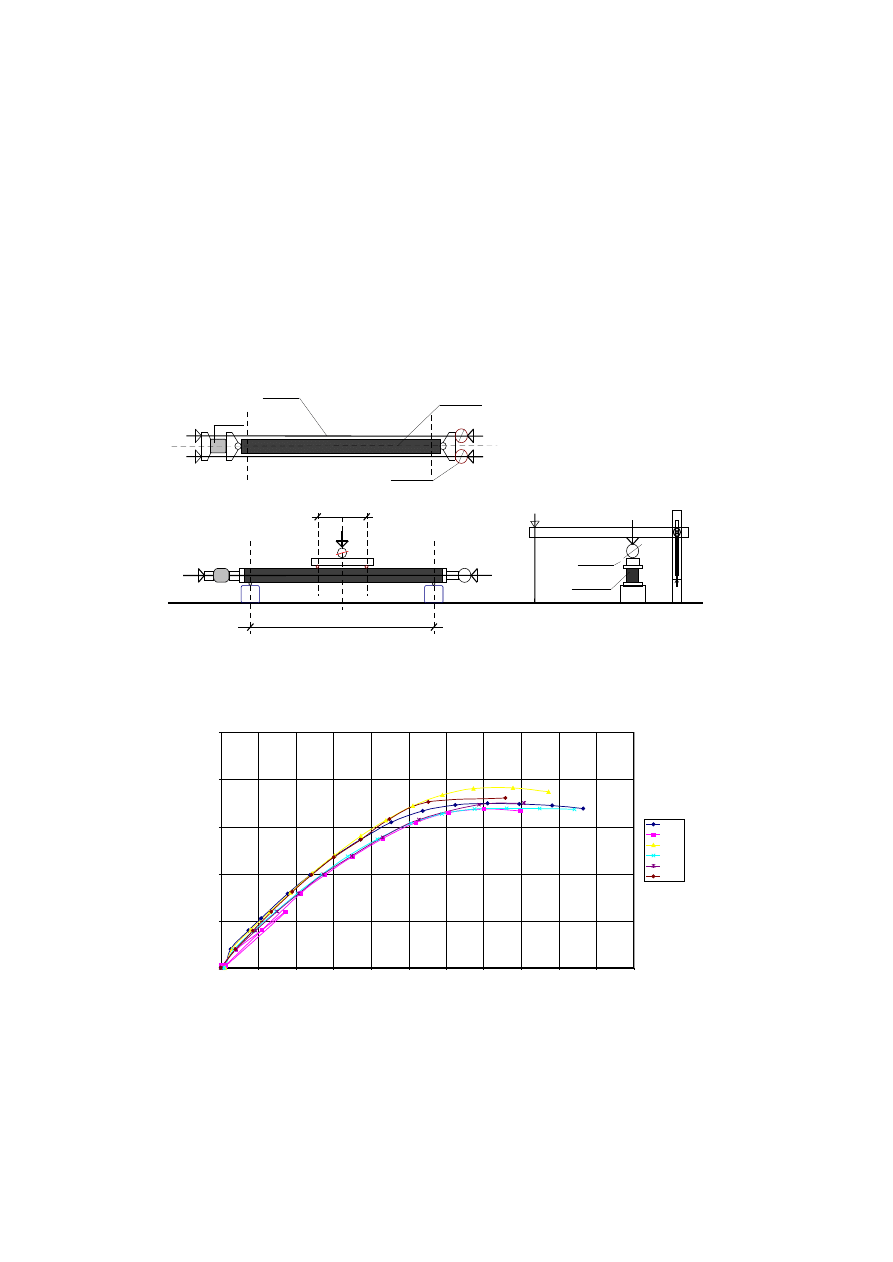
240

„Sterowanie siłą” stosowano do 160 kN (Rys.2), a pó źniej zamieniano na „sterowanie

przemieszczeniem” zwiększając je z przyrostem 10 mm. Pozioma siła ściskająca pozostawała
przez cały cykl badawczy taka sama i dzięki ciągłej kontroli i korekcie wynosiła 500 kN.

Specjalny siłomierz tensometryczny umieszczony pod ramieniem dźwigni umoż liwiał

pomiar obciążenia poprzecznego (rys. 1). Odkształcenia mierzono czujnikami tensomet-
rycznymi elektrooporowymi naklejonymi na stalowych pó łkach oraz na bocznych
powierzchniach betonowych. Pomiaru przemieszczeń dokonywano w środku rozpiętości
oraz pod siłami skupionymi stosując czujniki indukcyjne.

Cykl pomiarowy kończono po osiągnięciu maksimum obciążenia poprzecznego.

6000

P

H

H

1500

Silomierz

Badany slup

S3

P

S3

S1

S2

Silownik

Ciê gna

Badany slup

H/2

H/2

H/2

H/2

Silomierze

Rys. 1

Rys. 2

Wyniki pomiar

ó w przemieszczeń

0

50

100

150

200

250

0

1

2

3

4

5

6

7

8

9

10

11

Przemiescczenia [cm]

S

ił

a

[k

N

]

slup-6

slup-3

slup-4

slup-5

slup-2

slup-1

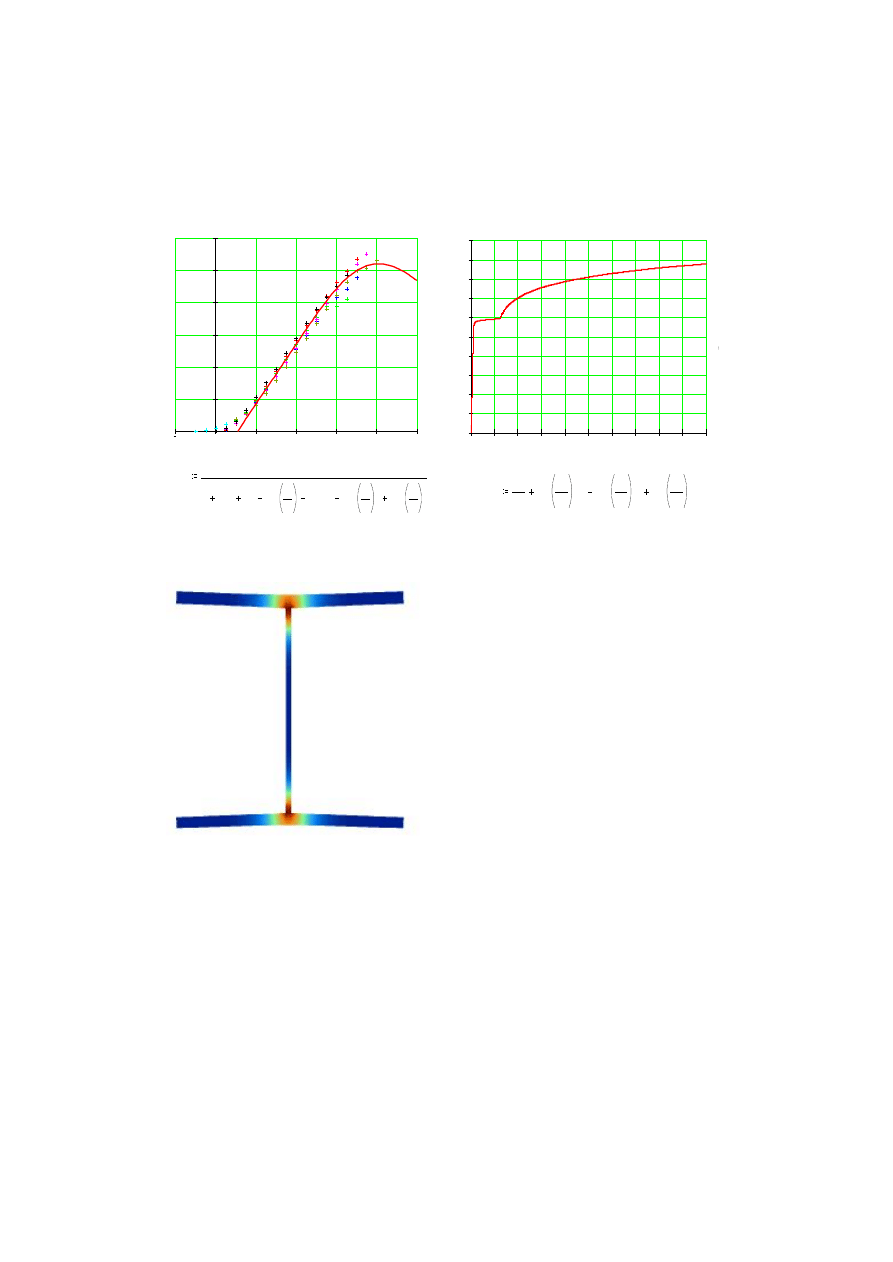
241

Prawa fizyczne betonu i stali z badań materiałowych

Rys. 3

Model obliczeniowy wymaga podania

pewnych informacji niezbędnych do przepro-
wadzenia obliczeń.

Podstawowymi danymi potrzebnymi do

poprawnego przygotowania i wykonania ob-
liczeń numerycznych opró cz geometrii, obcią-

ż eń i warunkó w brzegowych, są takż e para-
metry fizyczno-wytrzymałościowe materia-

łó w, z któ rych wykonano model tj. stali
i betonu. W tym celu zostały wykonane

odpowiednie badania materiałowe. Pomie-
rzono wytrzymałość i odkształcalność betonu

oraz wytrzymałość, granicę plastyczności
i wydłuż alność stali. Wyniki badań opraco-

wano i opisano – aproksymowano pewnymi

Rys. 4

zależ nościami funkcyjnymi przedstawionymi

na rys. 3.

Prawo fizyczne betonu dla napręż eń ściskających opisano znanym ró wnaniem

Saenza, a dla stali krzywą Remberga-Osgooda. Adaptując odpowiednio postać
ró wnania Remberga-Osgooda, któ re najczęściej stosowane jest w formie
„jednogałęziowej” krzywej, udało się dość precyzyjnie opisać klasyczną pełną postać
zależ ności

s-e

stali. Wyeksponowano wyraźnie pó łkę plastyczną i strefę

wzmocnienia. W podobny sposó b zaadaptowano ró wnanie Saenza i opisano prawo
fizyczne dla napręż eń rozciągających w betonie z uwzględnieniem charakterystycznej
części opadającej wykresu.

500

0

s

1

s

2

e s e s

,

0

0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1

50

100

150

200

250

300

350

400

450

500

Prawo fizyczne stali

N

ap

re

ze

ni

a

s e

( )

Eo

e

.

1

Ro Re

2

(

)

e

e

o

.

2

Ro

1

(

)

e

e

o

2

.

Ro

e

e

o

3

.

550

0

B1

B2

B3

B5

B6

B7

B8

1 1

(

)

1

0

1

2

3

4

5

100

200

300

400

500

600

Prawo fizyczne betonu (z badan)

S

ila

[k

N

]

e

2

s

2

(

)

s

o

Ea

e

p

s

o

Re

100

.

e

p

s

o

Re

10

.

e

p

s

2

Re

10

.

242

3. Modele teoretyczne

Modele teoretyczne konstrukcji zespolonych stalowych obetonowanych mogą być ró ż ne w
zależ ności od zastosowania, złoż oności konstrukcji i dostępnych narzędzi z zakresu
komputerowego wspomagania projektowania. Niewątpliwie innym modelem będzie
posługiwał się projektant konstrukcji szkieletowej stalowej obetonowanej, a innym badacz
przeprowadzający dokładniejszą teoretyczną identyfikację pola rozkładu przemieszczeń, sił
wewnętrznych lub tzw. „ścież ki ró wnowagi statycznej”, poró wnujący rezultaty swoich
rozważ ań z wynikami eksperymentu przeprowadzonego na modelu najczęściej jednego
elementu konstrukcyjnego.

Rezultaty dociekań teoretycznych i badań eksperymentalnych powinny z pewnością

w formie syntetycznej znaleźć zastosowanie w inż ynierskich aplikacjach projektowych, jako
ż e taki powinien być cel wszelkich badań.

Modelem, po któ ry sięgnie w końcu badacz, będzie niewątpliwie model dyskretny

konstrukcji oparty na metodzie elementó w skończonych z zastosowaniem prawdopodobnie
przestrzennego elementu skończonego. Posługując się odpowiednio potęż nym narzędziem
numerycznym np. systemem ABAQUS moż na uwzględnić w obliczeniach bardzo wiele
istotnych i mniej waż nych czynnikó w takich jak:

- nieliniowość praw fizycznych, a zwłaszcza betonu (rys. 3),
- asymetria fizyczna betonu polegająca na praktycznym braku wytrzymałości na

rozciąganie – wybó r odpowiedniej hipotezy wytrzymałościowej, postać powierzchni
plastyczności itp.,

- nieliniowość geometryczna – np. wpływ sił osiowych,
- napręż enia rezidualne tj. skurcz betonu , napręż enia spawalnicze (rys. 4, 5),
- cechy reologiczne betonu,
- zagadnienia kontaktowe na styku stal-beton itp.

Wadą tego modelu jest jednak to, ż e nie moż e on być zastosowany w praktyce projektowej,
ponieważ nakład pracy związany z modelowaniem i przygotowaniem danych nie będzie
wspó łmierny do efektó w, a i moż liwości obliczeniowe nawet tak duż ych systemó w są
ograniczone i nie ma praktycznej moż liwości obliczenia w ten sposó b całej typowej
rzeczywistej konstrukcji. Moż na jedynie obliczać pewne elementy lub fragmenty.
Wymodelowanie badanego i opisanego tutaj słupa za pomocą elementó w przestrzennych
SOLID wymagało ponad milion elementó w skończonych (0.56-1.60 mln), a utworzone pliki
pośrednie i pliki wynikó w skutecznie utrudniały pracę serwera (blokowały twarde dyski).

Projektant posługuje się zasadniczo modelami uproszczonymi z powodó w, któ re wyż ej

przedstawiono i w obliczeniach konstrukcji szkieletowej stosuje najczęściej model prętowy.
W tradycji inż ynierskiej model prętowy posiada mocną i ugruntowaną pozycję, a wszelkie
popularne numeryczne aplikacje inż ynierskie oparte są na tym modelu. Trudno się z tym nie
zgodzić, gdyż mimo pewnych wad posiada on wiele niezaprzeczalnych zalet, np. „dokładna”
postać funkcji kształtu i moż liwość obliczania skomplikowanych konstrukcji szkieletowych,
prętowych o duż ej liczbie elementó w.
W obliczeniach statycznych stalowych konstrukcji obetonowanych stosowany jest
najczęściej model przekroju sprowadzonego do przekroju stali lub betonu - przekroju
w pewnym sensie zhomogenizowanego, gdyż takie są wymagania aplikacji komputerowych.

Prezentowany model obliczania stalowych konstrukcji obetonowanych jest właśnie

zasadniczo oparty na modelu prętowym z pró bą uwzględnienia pewnych dodatkowych
czynnikó w istotnych dla konstrukcji zespolonych tego typu.

Pierwszym problemem jest niejednorodność przekroju. Jest on rozwiązywany za pomo-

cą specyficznej homogenizacji, pozwalającej na jednoczesne uwzględnienie niejednorodności

243

i nieliniowości fizycznej, szczegó lnie betonu. Celem homogenizacji jest ustalenie ogó lnej
postaci prawa fizycznego całego przekroju pręta

σ= f(ε)

(1)

któ re ze względó w praktycznych przyjmuje postać:

M = f(κ)

lub

B = f(κ)

(2)

gdzie:

B – sztywność przekroju

k

- krzywizna

Kolejnym problemem moż e być zmieniająca się na długości poszczegó lnych

elementó w (prętó w) sztywność przekroju, wynikająca, jak to wyż ej przedstawiono, ze
zmiany pola rozkładu sił wewnętrznych. Dobó r sztywności odbywa się iteracyjnie przy
zastosowaniu metody sztywności siecznej lub stycznej. Warunki zbież ności określono
dwoma sposobami.

W pierwszym z nich bada się zbież ność pola rozkładu sił wewnętrznych, a dokładnie

momentó w zginających. Uznaje się, ż e jeż eli pole rozkładu momentó w w następnym kroku
iteracyjnym nie zmienia się zasadniczo w stosunku do poprzedniego to oznacza, ż e w sposó b
„dostatecznie dokładny” dobrano sztywność przekrojó w. Praktycznie, dla ustalonego na
danym kroku iteracyjnym pola rozkładu sztywności, obliczane jest numerycznie pole
rozkładu momentó w zginających, a dokładnie rozkład średnich krzywizn. Ś rednią krzywiznę
określa się na podstawie trzech punktó w kwadratury Gaussa. Jednocześnie dla tego samego
pola rozkładu sztywności ustala się za pomocą uogó lnionego prawa fizycznego
odpowiadające momenty zginające i krzywizny oraz bada ich zbież ność:

|k

i

S

–

k

i

F

| <

e

(3)

gdzie:

k

i

S

– krzywizna obliczona na danym kroku iteracyjnym

k

i

F

– krzywizna z ró wnania fizycznego

k

=f(B)

W analizie posłuż ono się krzywizną, ponieważ funkcja B = f(

k

) jest monotoniczna w

przeciwieństwie do B = f(M), co pozwala ominąć problem nieokreśloności stycznej
macierzy sztywności w miejscu maksimum funkcji np. M = f(B) lub M = f(

d

). Sposó b

ten pozwala na prosty i łatwy opis stanó w pokrytycznych ró ż nych ścież ek ró wnowagi
statycznej.

Następnym problemem jest nieliniowość geometryczna związana z efektami II rzędu,

będąca wynikiem występowania znacznych sił osiowych, co w konstrukcjach szkieletowych
ma często miejsce. Problem ten rozwiązano przez rozbudowę macierzy sztywności o macierz
geometryczną zawierającą wspó łczynniki zależ ne od sił osiowych. W drugim wariancie
zastosowano „uaktualniony opis Lagrange’a” uwzględniający aktualną-bież ącą konfigurację
konstrukcji na danym kroku iteracyjnym.

(K

O

+ K

G

) u = P

(4)

gdzie:

K

O

– klasyczna macierz sztywności („spręż ysta”)

K

G

– geometryczna macierz sztywności

u , P - wektory przemieszczeń i sił węzłowych

244

Czwarty problem jest efektem dokładnej analizy wynikó w badań doświadczalnych.

Okazuje się bowiem, ż e dla dokładnego teoretycznego opisu pola rozkładu przemieszczeń
lub ścież ki ró wnowagi statycznej np. w postaci M = f(

d

) konieczna jest znajomość pola

rozkładu napręż eń rezidualnych, tj. napręż eń od skurczu betonu i napręż eń spawalniczych.

Napręż enia od skurcz betonu ustalono inż ynierską metodą Busemanna – metodą

włó kien pełzających. Założ ono, ż e siła skurczu betonu N

s

=

e

s

E

b

A

b

działa w środku

cięż kości przekroju betonowego jako zewnętrzna siła ściskająca cały przekró j zespolony.
Zastosowanie tej metody polega na rozważ eniu zachowania się dwó ch określonych włó kien
przekroju zespolonego i pozwala na rozprzęgnięcie ró wnań ró ż niczkowych np. Dischingera.
Włó kna dobrano w taki sposó b, aby siły w nich występujące nie oddziaływały wzajemnie
na siebie.

Ostateczny rozkład napręż eń w rdzeniu stalowym stanowi sumę wartości napręż eń od

siły pierwszego P

I

i drugiego P

II

włó kna. W betonie natomiast końcowe napręż enia są

superpozycją sumowania j/w oraz wartości napręż eń otrzymanych z obciążenia tylko
przekroju betonowego siłą rozciągającą N

s

.

Wynikiem obliczeń jest samoró wnoważ ący się stan napręż eń spowodowany skurczem

betonu w przekroju zespolonym.

Rys. 5

Dokładne empiryczne zbadanie rozkładu napręż eń spawalniczych nastręcza wiele

trudności i powinno stanowić przedmiot oddzielnych badań. Określenie numeryczne rozkła-
du napręż eń spawalniczych też nie jest proste i wymaga ustalenia wiarygodnych danych

245

i parametró w mających istotny wpływ na wyniki obliczeń. Na rys. 4 przedstawiono
rezultatyprzykładowych własnych obliczeń za pomocą MES-u pola rozkładu temperatur i
zakresu stref aktywnych powstałych w procesie spawania.

W obliczeniach teoretycznych posłuż ono się metodami inż ynierskimi ustalania

rozkładó w napręż eń spawalniczych, np. wg propozycji Okerbłoma.

Podstawowym celem w tej metodzie jest określenie wielkości tzw.„stref aktywnych”, to

jest obszaró w przekroju wokó ł spoin, w któ rych napręż enia osiągnęły granicę plastyczności.
Wielkości tych stref zależ ą od:

- liniowej energii spawania, któ ra w uproszczeniu jest funkcją grubości spoiny,
- parametró w geometrycznych przekroju,
- parametró w termo-mechanicznych materiału.

Napręż enia w strefach aktywnych są napręż eniami rozciągającymi ró wnymi granicy
plastyczności stali i powodują one pojawienie się napręż eń o przeciwnym znaku w
pozostałych częściach przekroju. Podobnie jak napręż enia skurczu betonu, napręż enia
spawalnicze są wewnętrznie zró wnoważ one, co oznacza spełnienie warunkó w:

S

A

i

s

i

= 0

S

A

i

s

i

y

i

= 0

(5)

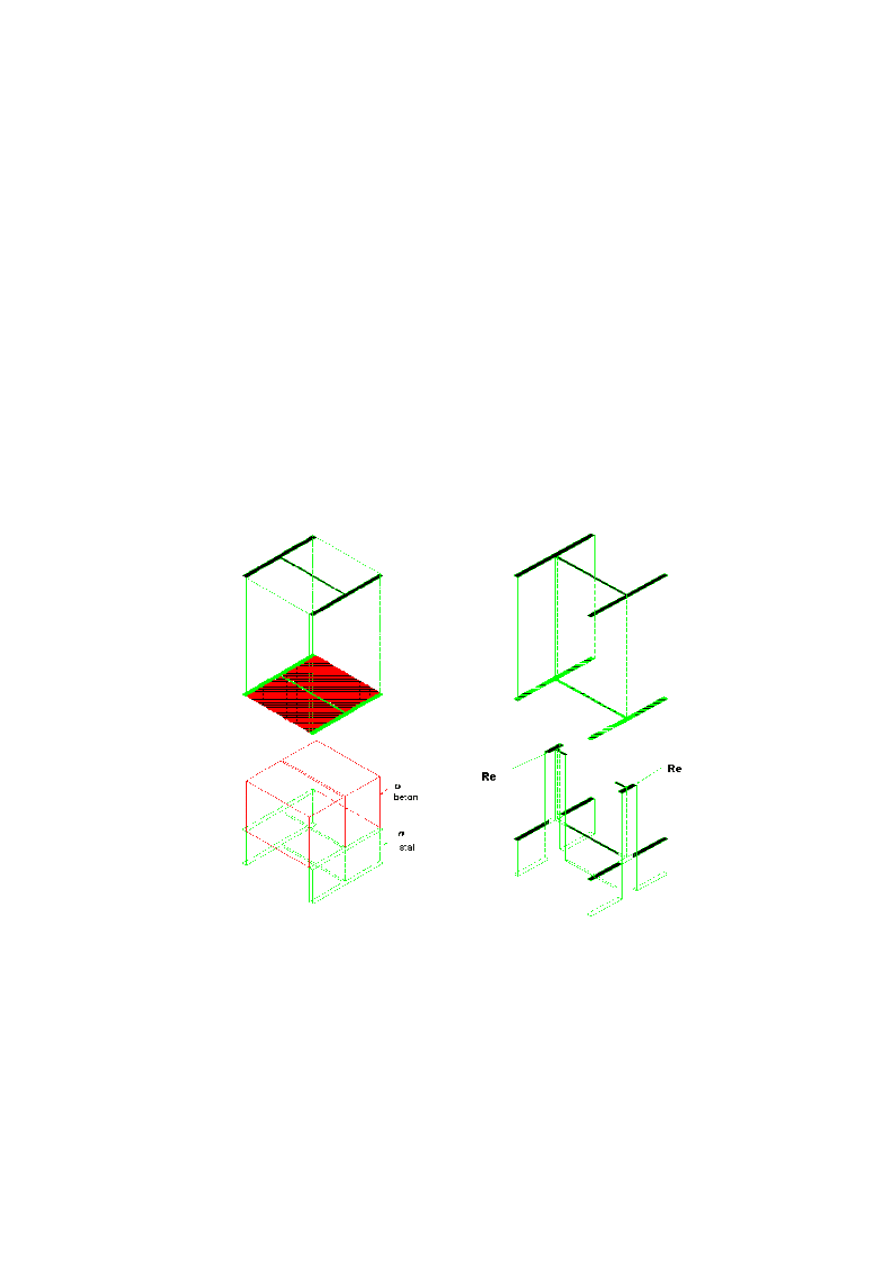
Na rys.5 przedstawiono schematycznie rozkład napręż eń rezidualnych, tj. od skurczu

betonu i spawalniczych, traktowanych jako stan początkowy – inicjujący przy obliczaniu
poszczegó lnych wartości uogó lnionego prawa fizycznego dla zhomogenizowanego przekroju
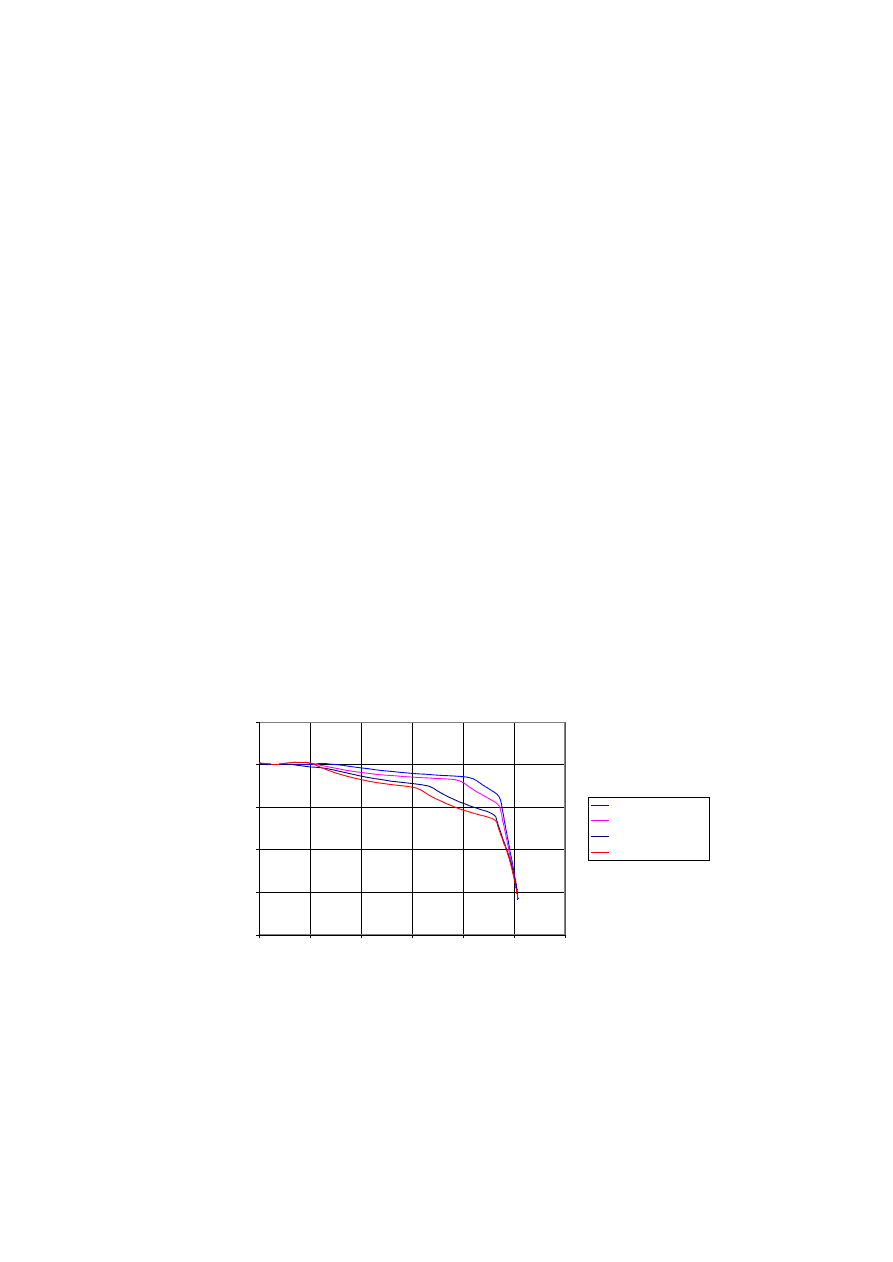
zespolonego. Na wykresie niż ej (rys. 6) przedstawiono wpływ uwzględnienia lub pominięcia
napręż eń rezidualnych na postać uogó lnionego prawa fizycznego, a na ostatnim wykresie
(rys. 7) poró wnano wyniki badań eksperymentalnych słupó w obetonowanych (przemiesz-
czeń) z wynikami obliczeń teoretycznych, w któ rych uwzględniono lub nie napręż enia
spawalnicze i napręż enia od skurczu betonu.

Rys. 6

EJ = f(M)

0

50000000

100000000

150000000

200000000

250000000

0

5000

10000

15000

20000

25000

30000

Momenty M

S

z

ty

w

n

o

s

c

i

E

J

Bez napr

ęż eń rezid.

Skurcz

Spawalnicze

Spawalnicz+skurcz

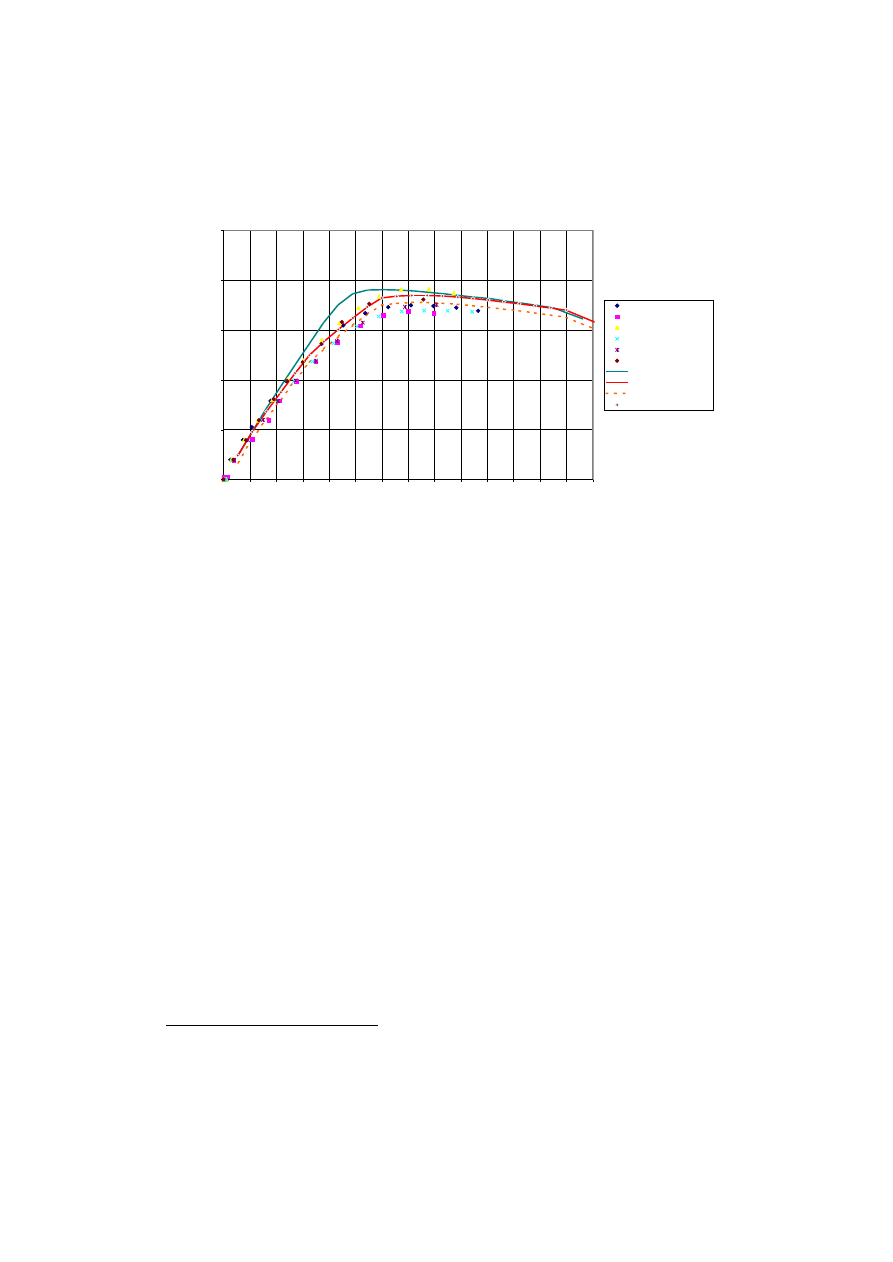
246

Rys. 7

4. Podsumowanie

Zaprezentowany sposó b obliczania konstrukcji stalowych zespolonych, obetonowanych,
oparty na tradycyjnym modelu prętowym, dzięki wprowadzeniu odpowiednich modyfikacji,
moż e stanowić dobre narzędzie w obliczeniach inż ynierskich, a jako model teoretyczny
pozwala eksperymentatorowi wystarczająco dokładnie identyfikować rezultaty badań
doświadczalnych.

Literatura

[1]

Ł ODYGOWSKI T., SZUMIGAŁ A M., Engineering Models for Numerical Analysis of
Composite Bending Members. Mech. Struct. & Mach., 20 (3), s. 363-380 (1992).

[2] SZUMIGAŁ A M., Numerical analysis of composite beams loaded eccenrically. XIII

Polish Conference on Computer Methods in Mechanics. Poznań 1997, Vol. 4, s. 1233-124.

BAR AND TREE-DIMENSIONAL MODELS OF ENCASED

STEEL ELEMENT IN VIEW OF EXPERIMENTAL RESULTS

Summary

The theoretical model of composite steel-concrete element is presented in this paper. The
traditional theoretical bar model has been modified and the following problems have been
taken into consider action: residual stresses (concrete shrinkage, welding stresses),
changeability of the cross section stiffness, nonlinear behavior of structure, homogenization
and conctitutive law for the whole cross section in generalized form moment-curvature.

Pracę wykonano w ramach tematu badawczego BW-11-164/2002

Wyniki pomiar

ó w przemieszczeń - obliczenia teoretyczne

0

50

100

150

200

250

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

Przemiescczenia [cm]

S

ił

a

[k

N

]

slup-6

slup-3

slup-4

slup-5

slup-2

slup-1

bez napr. rezidualnych

skurcz+spawalnicze

po uwzgl. Ci

ęż aru włas.

Uaktual. opis Lagrangea