
POLITECHNIKA ŚWIĘTOKRZYSKA
w Kielcach
WYDZIAŁ MECHATRONIKI I BUDOWY MASZYN
ZAKŁAD MECHATRONIKI
LABORATORIUM PODSTAW AUTOMATYKI
INSTRUKCJA
ĆWICZENIE LABORATORYJNE NR 2
Temat: Badania symulacyjne podstawowych członów automatyki
(wyznaczanie odpowiedzi na wymuszenie skokowe) cz.2
Opracował:
dr inż. Paweł Łaski
Kielce 2006

Cel Ćwiczenia
Wyznaczyć:
1. Odpowiedź skokową.
2. Charakterystykę amplitudowo częstotliwościową.
3. Charakterystykę fazowo częstotliwościową.
4. Charakterystykę amplitudowo fazową (wykres Nyquista).
5. Składowe rzeczywistą i urojoną transmitancji.
6. Logarytmiczną charakterystykę amplitudowo częstotliwościową.
7. Logarytmiczną charakterystykę fazowo częstotliwościową.
8. Logarytmiczną charakterystykę amplitudowo fazową (wykres Blacka)
dla
następujących członów automatyki:
- oscylacyjnego II-go rzędu
- szeregowo
połączonych całkującego idealnego z oscylacyjnym II-go rzędu
1. Wyznaczyć odpowiedź y(t) na wymuszenie skokowe członu oscylacyjnego II rzędu.
Zadanie rozwiązać dla następujących danych: T=0,1[s],
10
,
1
,
5
.
0
,
01
.
0
4
3
2
1
=
=
=
=
ξ
ξ
ξ
ξ
k=2,
,
)
(
1
)
(
t
X
t
x
st
⋅
=
1
=
st
X
Transmitancja operatorowa członu oscylacyjnego II-go rzędu
1
2
)
(
)
(
)
(
2
2
+
⋅
⋅
+
⋅
=
=
s
T
s
T
k
s
X
s
Y
s
G
ξ
)
(
1
2
)
(
)
(
)
(
2
2
s
X
s
T
s
T
k
s
X
s
G
s
Y
⋅
+
⋅
⋅
+
⋅
=
⋅
=
ξ
s
x
s
X
t
x
t
x
st
st
1
)
(
)
(
1
)
(
⋅
=
⇒
⋅
=
(
)
1
2
1
1
2
)
(
)
(
)
(
2
2
2
2
+
⋅
⋅
+
⋅
⋅
⋅
=
⋅
⋅
+
⋅
⋅
+
⋅
=
⋅
=
s
T
s
T
s
x
k
s
x
s
T
s
T
k
s
X
s
G
s
Y
st
st
ξ
ξ
Sposób pierwszy: analityczny
Po przejściu z transformaty Laplace’a
do postaci czasowej y(t) otrzymujemy zależność
opisującą odpowiedź skokową członu oscylacyjnego II-go rzędu
)
(s
Y
dla
ξ
<1:
( )
[
]
(
)
(
)
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+
⋅
−
⋅
−
−
⋅
⋅
+
=
=
⎥
⎦
⎤
⎢
⎣
⎡
+
⋅
⋅
+
⋅
⋅
⋅
⋅
⋅
=
⎥
⎦
⎤
⎢
⎣
⎡
+
⋅
⋅
+
⋅
⋅
⋅
=
=
⋅
−
−
−
−
ξ
ξ
ξ
ξ
ξ
ξ
ξ
2
2
2
0
2
2
1
2
2
1
1
1
ctg
1
sin
1
1
1
2
1
2
)
(
ar
T
t
e
x
k
y
s
T
s
T
s
x
k
L
x
k
s
T
s
T
s
x
k
L
s
Y
L
t
y
t
T
st
st
st
st
dla
ξ=
1:
( )
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⋅
⎟
⎠
⎞
⎜
⎝
⎛ +
−
⋅
⋅
+
=
−
T
t
st
e
T
t
x
k
y
t
y
1
1
0
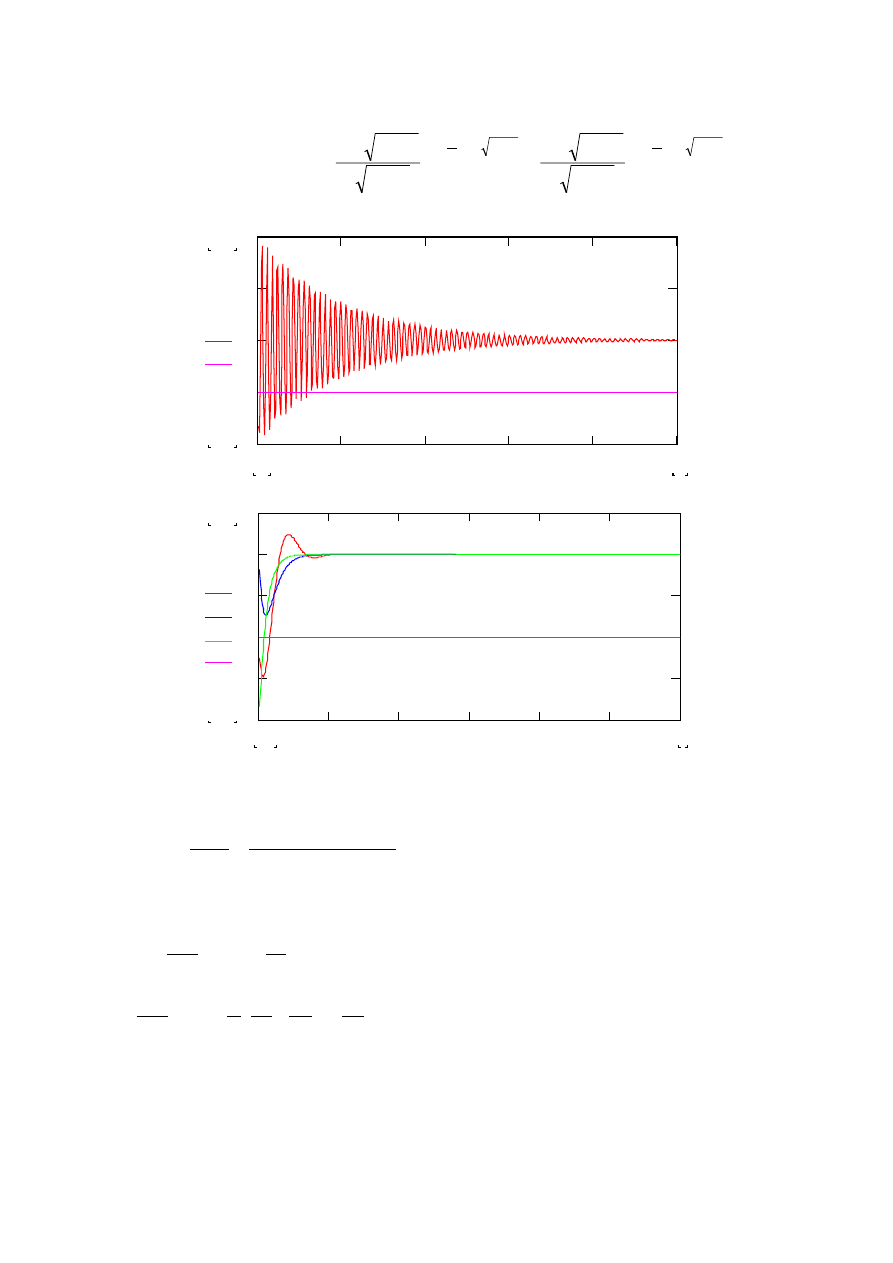
dla
ξ>
1:
( )
(
)
(
)
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⋅
−
−
+
−
⋅
−
−
−
+
⋅
⋅
+
=
−
−
⋅
−
−
+
⋅
−
1
2
2
1
2
2
0
2
2
1
2
1
1
2
1
1
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
T
t
T
t
st
e
e
x
k
y
t
y
0
10
20
30
40
0
1
2
3
4
50
3.819
0.176
y 1 t
( )
x t
( )
50
0.1
t
0
1
2
3
4
5
6
0
0.5
1
1.5
2
2.5
2.241
0.165
y 2 t
( )
y 3 t
( )
y 4 t
( )
x t
( )
6
0.01
t
Sposób drugi: numeryczny
1
2
)
(
)
(
)
(
2
2
+
⋅
⋅
+
⋅
=
=
s
T
s
T
k
s
X
s
Y
s
G
ξ
( )
( ) ( )
( )
s
X
k
s
Y
s
Y
s
T
s
Y
s
T
⋅
=
+
⋅
⋅
⋅
+
⋅
⋅
ξ
2
2
2
( )
t
x
k
y
dt
dy
T
dt
y
d
T
⋅
=
+
⋅
⋅
+
⋅
ξ
2
2
2
2
( )
t
x
T
k
y
T
dt
dy
T
dt
y
d
⋅
+
−
⋅
⋅
−
=
2
2
2
2
1
1
2
ξ
Wprowadzamy oznaczenie
i otrzymujemy układ równań:
1
y
y
≡
⎪
⎪
⎩
⎪
⎪
⎨
⎧
⋅
+
⋅
−
⋅
−
=
=
)
(
1
2
2
1
2
2
2
2
1
t
x
T
k
y
T
y
T
dt
dy
y
dt
dy
ξ
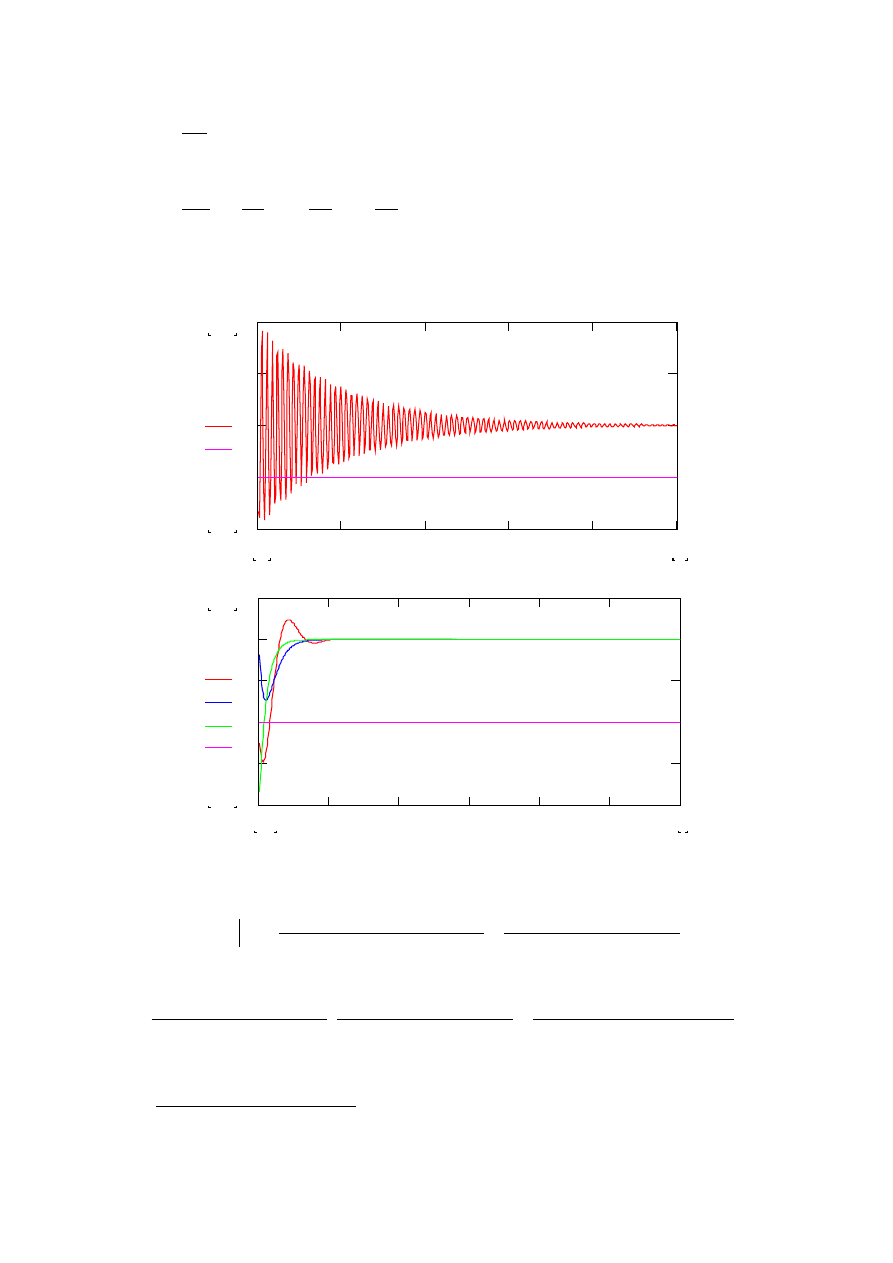
Rozwiązując numerycznie powyższy układ równań wyznaczamy odpowiedź członu
oscylacyjnego II-go rzędu na skok jednostkowy.
2
,
1
,
5
.
0
,
01
.
0
4
3
2
1
=
=
=
=
ξ
ξ
ξ
ξ
.
0
10
20
30
40
0
1
2
3
4
50
3.819
0.176
y 1 t
( )
x t
( )
50
0.1
t
0
1
2
3
4
5
6
0
0.5
1
1.5
2
2.5
2.241
0.165
y 2 t
( )
y 3 t
( )
y 4 t
( )
x t
( )
6
0.01
t
Charakterystyka amplitudowo częstotliwościowa A(
ω).
Transmitancja widmowa członu oscylacyjnego II-go rzędu
(
)
(
)
(
)
(
)
)
(
)
(
4
1
2
4
1
1
2
1
2
1
2
1
2
1
1
2
)
(
)
(
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
ω
ω
ω
ξ
ω
ω
ξ
ω
ξ
ω
ω
ω
ξ
ω
ω
ξ
ω
ω
ξ
ω
ω
ξ
ω
ω
ξ
ω
ω
ω
Q
j
P
T
T
T
k
j
T
T
T
k
j
T
T
j
T
T
j
T
T
k
j
T
T
k
j
T
j
T
k
s
G
j
G
j
s
⋅
+
=
⋅
⋅
+
⋅
−
⋅
⋅
⋅
−
⋅
+
⋅
⋅
+
⋅
−
⋅
−
⋅
=
⋅
⋅
⋅
−
⋅
−
⋅
⋅
⋅
−
⋅
−
⋅
⋅
⋅
⋅
+
⋅
−
=
=
⋅
⋅
⋅
+
⋅
−
=
+
⋅
⋅
⋅
+
⋅
⋅
=
=
gdzie:
(
)
(
)
2
2
2
2
2
2
2
2
4
1
1
)
(
ω
ξ
ω
ω
ω
⋅
⋅
+
⋅
−
⋅
−
⋅
=
T
T
T
k
P
składowa rzeczywista transmitancji widmowej
(
)
2
2
2
2
2
2
4
1
2
)
(
ω
ξ
ω
ω
ξ
ω
⋅
⋅
+
⋅
−
⋅
⋅
⋅
−
=
T
T
T
k
Q
składowa urojona transmitancji widmowej
Transmitancja widmowa członu oscylacyjnego II-go rzędu
( )
(
)
(
)
(
)
(
)
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
4
1
4
1
2
4
1
1
)
(
)
(
)
(
)
(
)
(
)
(
ω
ξ
+
ω
⋅
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ω
ξ
+
ω
⋅
−
ω
⋅
⋅
ξ
⋅
−
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ω
ξ
+
ω
⋅
−
ω
⋅
−
⋅
=
=
ω
+
ω
=
ω
⋅
+
ω
=
ω
=
ω
=
ω
T
T
k
T
T
T
k
T
T
T
k
Q
P
Q
j
P
j
G
f
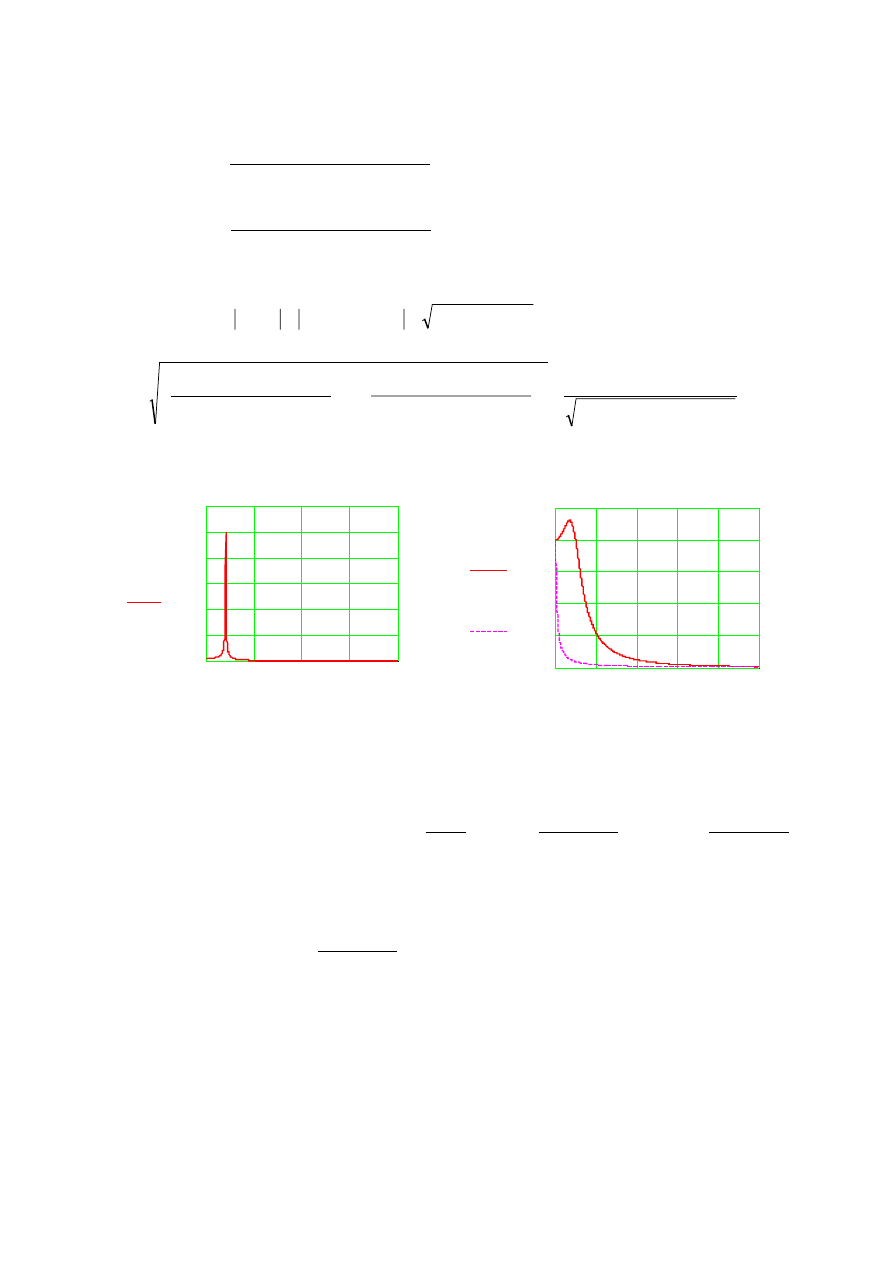
A
moduł transmitancji widmowej
A 1 ω
(
)
ω
0
25
50
75
100
0
20
40
60
80
100
120
A 2 ω
(
)
A 3 ω
(
)
A 4 ω
(
)
ω
0
20
40
60
80
100
0
0.5
1
1.5
2
2.5
Charakterystyka fazowo częstotliwościowa
( )
ω
ϕ
.
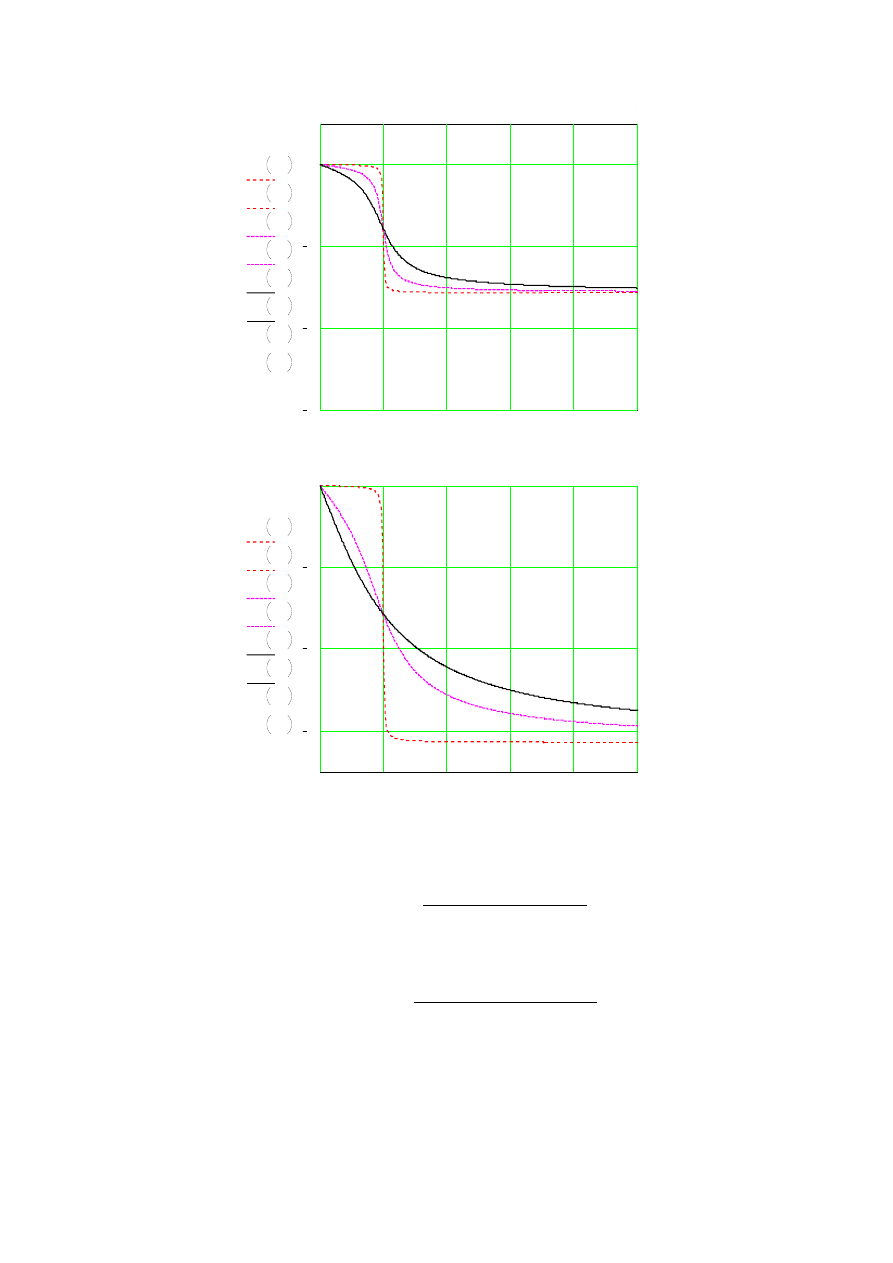
Argument transmitancji widmowej
Dla II ćwiartki w której
0
)
(
0
)
(
>
<
ω
ω
P
i
Q
( )
( )
( )
[
]
⎟
⎠
⎞
⎜
⎝
⎛
⋅
−
⋅
⋅
−
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅
−
⋅
⋅
−
=
=
=
=
2
2
2
2
1
2
tg
1
2
tg
)
(
)
(
tg
arg
ω
ω
ξ
ω
ω
ξ
ω
ω
ω
ω
ω
ϕ
T
T
arc
T
T
arc
P
Q
arc
j
G
f
Dla III ćwiartki w której
0
)
(
0
)
(
<
ω
<
ω
P
i
Q
( )
⎟
⎠
⎞
⎜
⎝
⎛
⋅
−
⋅
⋅
−
−
=
2
2
1
2
tg
ω
ω
ξ
π
ω
ϕ
T
T
arc
φ 1 ω 1
φ 2 ω 2
φ 3 ω 3
φ 4 ω 4
φ 5 ω 5
φ 6 ω 6
φ 7 ω 7
φ 8 ω 8
ω 1 ω 2
,
ω 3
,
ω 4
,
ω 5
,
ω 6
,
ω 7
,
ω 8
,
0
10
20
30
40
50
6
4
2
0
φ 1 ω 1
φ 2 ω 2
φ 3 ω 3
φ 4 ω 4
φ 5 ω 5
φ 6 ω 6
φ 7 ω 7
φ 8 ω 8
ω 1 ω 2
,
ω 3
,
ω 4
,
ω 5
,
ω 6
,
ω 7
,
ω 8
,
0
10
20
30
40
50
3
2
1
0
Charakterystyka amplitudowo fazowa (wykres Nyquista).
Składowa urojona transmitancji widmowej
(
)
2
2
2
2
2
2
4
1
2
)
(
ω
ξ
+
ω
⋅
−
ω
⋅
⋅
ξ
⋅
−
=
ω
T
T
T
k
Q
Składowa rzeczywista transmitancji widmowej
(
)
(
)
2
2
2
2
2
2
2
2
4
1
1
)
(
ω
ξ
ω
ω
ω
T
T
T
k
P
+
⋅
−
⋅
−
⋅
=
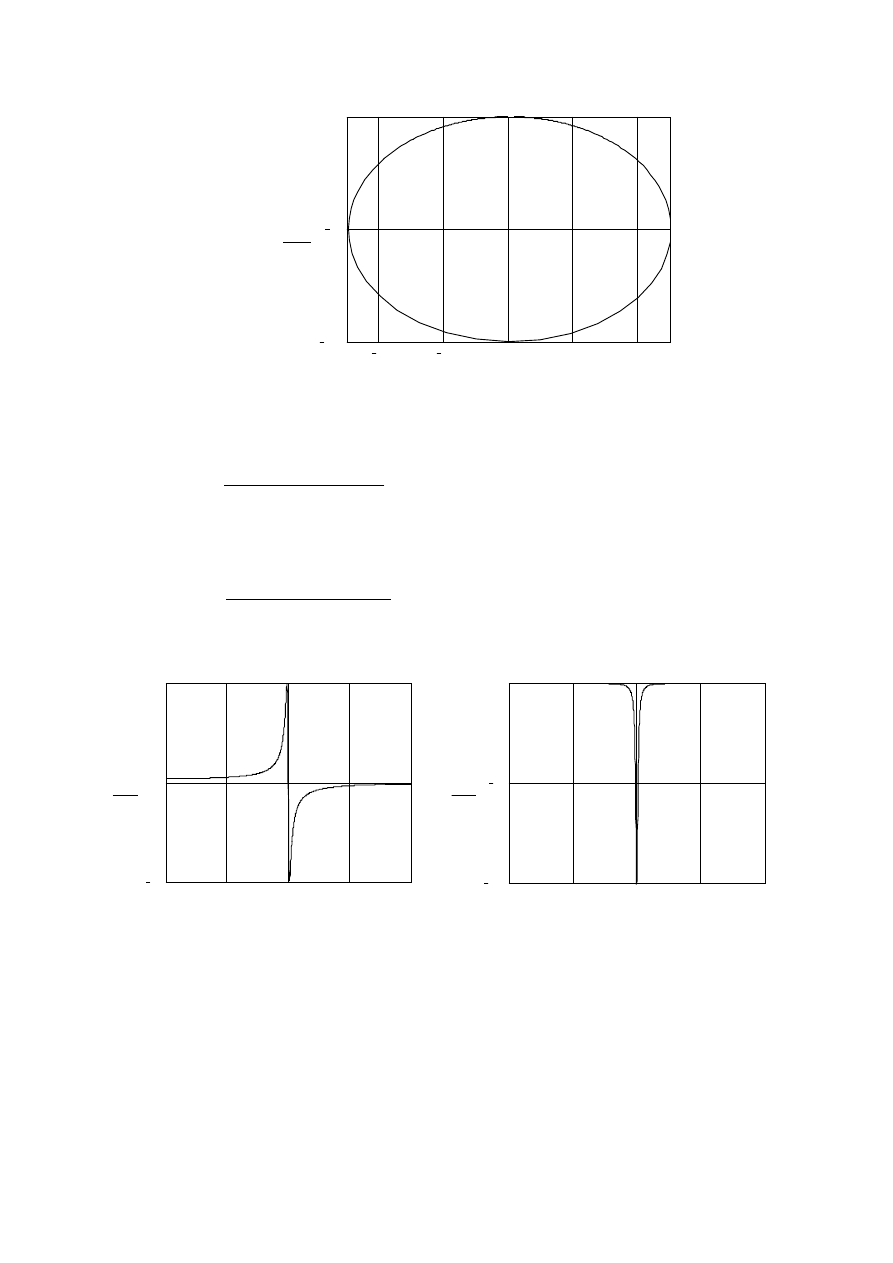
Q
ω
( )
P
ω
( )
40
20
0
20
40
100
50
0
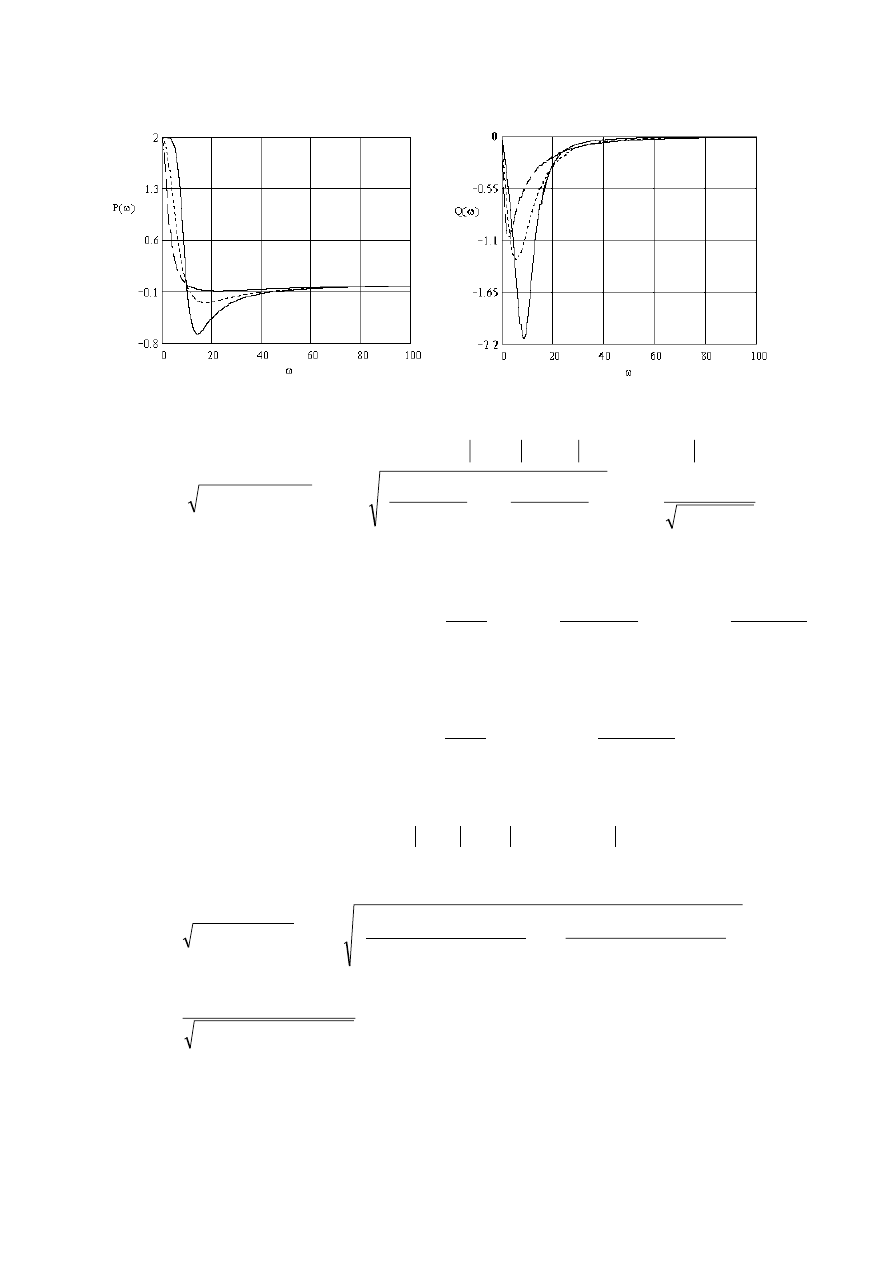
Składowe rzeczywista i urojona transmitancji.
Składowa rzeczywista transmitancji widmowej
(
)
(
)
2
2
2
2
2
2
2
2
4
1
1
)
(
ω
ξ
+
ω
⋅
−
ω
⋅
−
⋅
=
ω
T
T
T
k
P
Składowa urojona transmitancji widmowej dla
2
,
1
,
5
.
0
,
01
.
0
4
3
2
1
=
=
=
=
ξ
ξ
ξ
ξ
(
)
2
2
2
2
2
2
4
1
2
)
(
ω
ξ
+
ω
⋅
−
ω
⋅
⋅
ξ
⋅
−
=
ω
T
T
T
k
Q
P
ω
( )
ω
0
5
10
15
20
50
0
50
Q
ω
( )
ω
0
5
10
15
20
100
50
0
Logarytmiczna charakterystyka amplitudowo częstotliwościowa.
( )
( )
( )
1
lg
20
1
1
lg
20
)
(
)
(
lg
20
)
(
)
(
lg
20
)
(
lg
20
)
(
lg
20
lg
2
2
2
2
2
2
2
2
2
2
1
+
⋅
=
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
⋅
⋅
−
+
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
=
+
=
=
⋅
+
=
=
=
=
=
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
T
k
T
T
k
T
k
Q
P
Q
j
P
j
G
A
M
f
Lm
Logarytmiczna charakterystyka fazowo częstotliwościowa.
Dla IV ćwiartki w której
0
)
(
0
)
(
>
ω
<
ω
P
i
Q
( )
( )
( )
[
]
⎟
⎠
⎞
⎜
⎝
⎛
⋅
−
⋅
⋅
−
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅
−
⋅
⋅
−
=
=
=
=
2
2
2
2
2
1
2
tg
1
2
tg
)
(
)
(
ctg
arg
lg
ω
ω
ξ
ω
ω
ξ
ω
ω
ω
ω
ω
ϕ
T
T
arc
T
T
arc
P
Q
ar
j
G
f
Dla III ćwiartki w której
0
)
(
0
)
(
<
ω
<
ω
P
i
Q
( )
( )
( )
[
]
⎟
⎠
⎞
⎜
⎝
⎛
⋅
−
⋅
⋅
+
−
=
=
=
=
2
2
2
1
2
tg
)
(
)
(
ctg
arg
lg
ω
ω
ξ
π
ω
ω
ω
ω
ω
ϕ
T
T
arc
P
Q
ar
j
G
f
Logarytmiczna charakterystyka amplitudowo fazowa (wykres Blacka).
Logarytmiczna charakterystyka modułu
( )
( )
( )
(
)
(
)
(
)
(
)
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
1
4
1
lg
20
4
1
2
4
1
1
lg
20
)
(
)
(
lg
20
)
(
)
(
lg
20
)
(
lg
20
)
lg(
20
lg
ω
ξ
+
ω
⋅
−
=
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ω
ξ
+
ω
⋅
−
ω
⋅
⋅
ξ
⋅
−
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ω
ξ
+
ω
⋅
−
ω
⋅
−
⋅
=
ω
+
ω
=
=
ω
⋅
+
ω
=
ω
=
ω
=
ω
=
ω
=
ω
T
T
k
T
T
T
k
T
T
T
k
Q
P
Q
j
P
j
G
M
f
Lm
Logarytmiczna charakterystyka fazy
Dla IV ćwiartki w której
0
)
(
0
)
(
>
ω
<
ω
P
i
Q

( )
(
)
( )
[
]
⎟
⎠
⎞
⎜
⎝
⎛
⋅
−
⋅
⋅
−
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅
−
⋅
⋅
−
=
=
=
=
2
2
2
2
2
1
2
tg
1
2
tg
)
(
)
(
ctg
arg
lg
ω
ω
ξ
ω
ω
ξ
ω
ω
ω
ω
ω
ϕ
T
T
arc
T
T
arc
P
Q
ar
j
G
f
Dla III ćwiartki w której
0
)
(
0
)
(
<
ω
<
ω
P
i
Q
( )
⎟
⎠
⎞
⎜
⎝
⎛
⋅
−
⋅
⋅
+
−
=
2
2
1
2
tg
ω
ω
ξ
π
ω
ϕ
T
T
arc
2. Wyznaczyć odpowiedź y(t) na wymuszenie skokowe szeregowo połączonych członów
całkującego idealnego z oscylacyjnym II-go rzędu skokowa.
Zadanie rozwiązać dla następujących danych: T=0,1[s],
[ ]
s
T
c
1
,
0
=
,
1
.
0
=
ξ
k=1,
,
)
(
1
)
(
t
X
t
x
st
⋅
=
1
=
st
X
Transmitancja operatorowa szeregowo połączonych członów całkującego idealnego z
oscylacyjnym II-go rzędu
(
)
1
2
1
)
(
)
(
)
(
2
2
+
⋅
⋅
+
⋅
⋅
⋅
=
=
s
T
s
T
k
s
T
s
X
s
Y
s
G
c
ξ
Sposób pierwszy: analityczny
(
)
)
(
1
2
1
)
(
)
(
)
(
2
2
s
X
s
T
s
T
s
T
k
s
X
s
G
s
Y
c
⋅
+
⋅
⋅
+
⋅
⋅
⋅
=
⋅
=
ξ
st
st
x
s
s
X
t
x
t
x
⋅
=
⇒
⋅
=
1
)
(
)
(
1
)
(
(
)
(
)
1
2
1
)
(
1
2
1
)
(
)
(
)
(
2
2
2
2
2
+
⋅
⋅
+
⋅
⋅
⋅
⋅
=
⋅
+
⋅
⋅
+
⋅
⋅
⋅
=
⋅
=
s
T
s
T
s
T
x
k
s
X
s
T
s
T
s
T
k
s
X
s
G
s
Y
c
st
c
ξ
ξ
Po przejściu od transformaty Laplace’a
(
)
1
2
1
)
(
2
2
2
+
⋅
⋅
+
⋅
⋅
⋅
⋅
=
s
T
s
T
s
T
x
k
s
Y
c
st
ξ
do postaci
czasowej otrzymujemy zależność opisującą odpowiedź skokową członu oscylacyjnego II-go
rzędu
( )
[
]
(
)
(
)
⎥
⎦
⎤
⎢
⎣
⎡
+
⋅
⋅
+
⋅
⋅
⋅
⋅
=
⎥
⎦
⎤
⎢
⎣
⎡
+
⋅
⋅
+
⋅
⋅
⋅
⋅
=
=
−
−
−
1
2
1
1
2
1
)
(
2
2
2
1
2
2
2
1
1
s
T
s
T
s
L
T
x
k
s
T
s
T
s
T
x
k
L
s
Y
L
t
y
c
st
c
st
ξ
ξ
Transformaty
(
)
1
2
1
2
2
2
+
⋅
⋅
+
⋅
⋅
s
T
s
T
s
ξ
nie ma w tablicach transformat. Rozkładamy ją więc
na ułamki proste.
(
)
(
)
1
2
1
2
1
2
1
2
2
2
2
2
2
2
2
+
⋅
⋅
+
⋅
+
+
⋅
⋅
+
⋅
⋅
+
=
+
⋅
⋅
+
⋅
⋅
s
T
s
T
C
s
T
s
T
s
B
s
A
s
T
s
T
s
ξ
ξ
ξ
Mnożymy lewą i prawą stronę przez
(
)
1
2
2
2
2
+
⋅
⋅
+
⋅
⋅
s
T
s
T
s
ξ
(
)
2
2
2
1
2
1
s
C
s
B
s
T
s
T
A
⋅
+
⋅
+
+
⋅
⋅
+
⋅
⋅
=
ξ
(
)
A
s
B
T
A
s
C
T
A
+
⋅
+
⋅
⋅
+
⋅
+
⋅
=
ξ
2
(
)
1
2
2
(
)
0
1
2
2
0
1
2
2
(
)
1
0
0
s
A
s
B
T
A
s
C
T
A
s
s
s
⋅
+
⋅
+
⋅
⋅
+
⋅
+
⋅
=
⋅
+
⋅
+
⋅
ξ
⎪
⎩
⎪
⎨
⎧
=
+
⋅
⋅
=
+
⋅
=
A
B
T
A
C
T
A
1
2
0
0
2
ξ
Stąd A=1, B=
T
ξ
2
−
, C=
2
T
−
(
)
(
)
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
⋅
⋅
+
⋅
−
+
+
⋅
⋅
+
⋅
⋅
−
+
⋅
⋅
=
=
⎥
⎦
⎤
⎢
⎣
⎡
+
⋅
⋅
+
⋅
+
+
⋅
⋅
+
⋅
⋅
+
⋅
⋅
=
1
2
1
2
2
1
1
2
1
2
)
(
2
2
2
2
2
2
2
2
2
2
2
s
T
s
T
T
s
T
s
T
s
T
s
T
x
k
s
T
s
T
C
s
T
s
T
s
B
s
A
T
x
k
s
Y
c
st
c
st
ξ
ξ
ξ
ξ
ξ
Korzystamy z tablic transformat Laplace’a:
( )
(
)
(
)
⎪
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎪
⎬
⎫
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎨
⎧
⎟
⎠
⎞
⎜
⎝
⎛
⋅
−
⋅
⋅
−
−
+
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+
⋅
−
⋅
⋅
−
−
⋅
⋅
−
⋅
⋅
+
=
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
⋅
⋅
+
⋅
−
+
+
⋅
⋅
+
⋅
⋅
−
+
⋅
⋅
=
=
⎥
⎦
⎤
⎢
⎣
⎡
+
⋅
⋅
+
⋅
⋅
⋅
⋅
=
⋅
−
⋅
−
−
−
T
t
e
T
ar
T
t
e
T
t
T
x
k
y
s
T
s
T
T
s
T
s
T
s
T
s
L
T
x
k
s
T
s
T
s
L
T
x
k
t
y
T
t
T
t
c
st
c
st
c
st
2
2
2
2
2
0
2
2
2
2
2
2
1
2
2
2
1
1
sin
1
1
ctg
1
sin
1
1
1
2
1
2
1
2
2
1
1
2
1
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
ξ
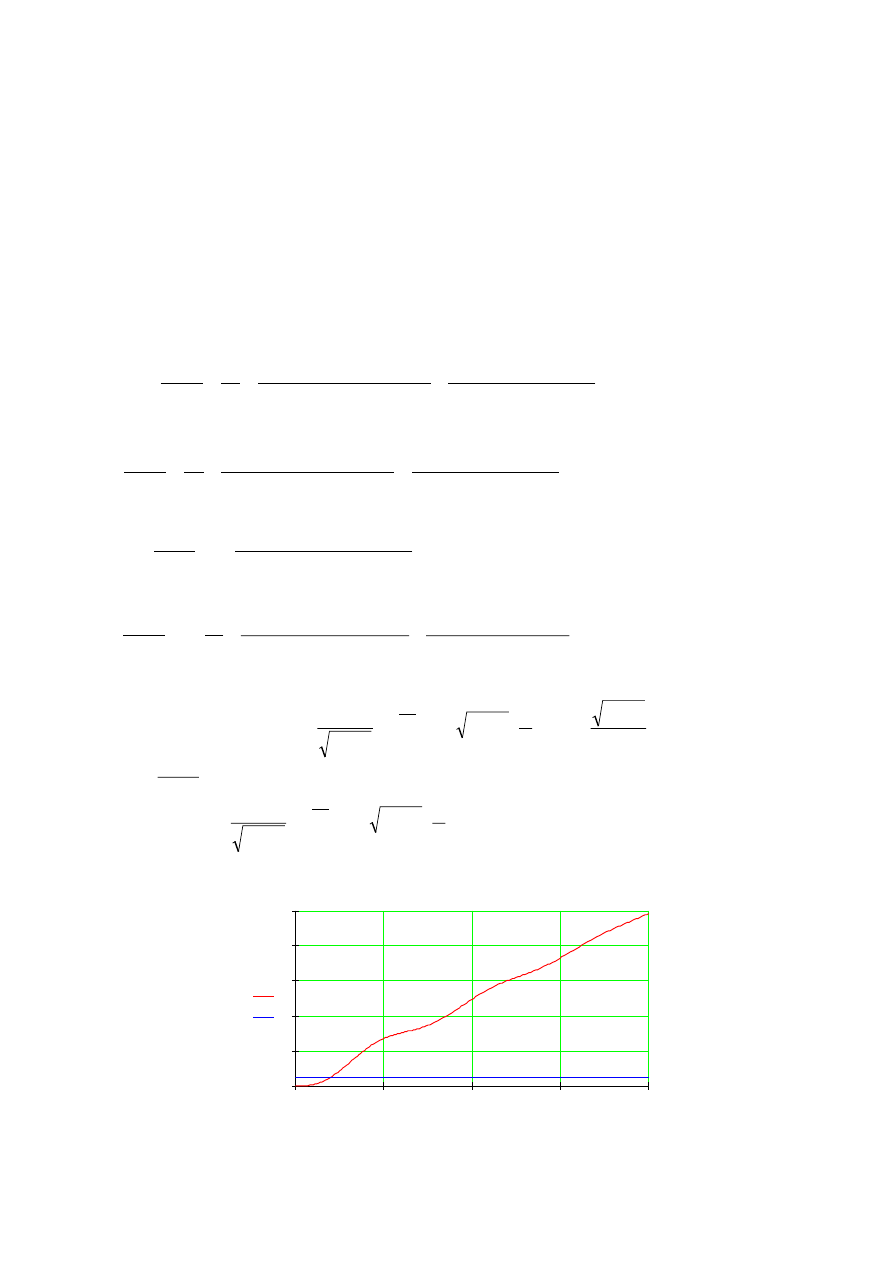
y t
( )
x t
( )
t
0
0.5
1
1.5
2
4
8
12
16
20
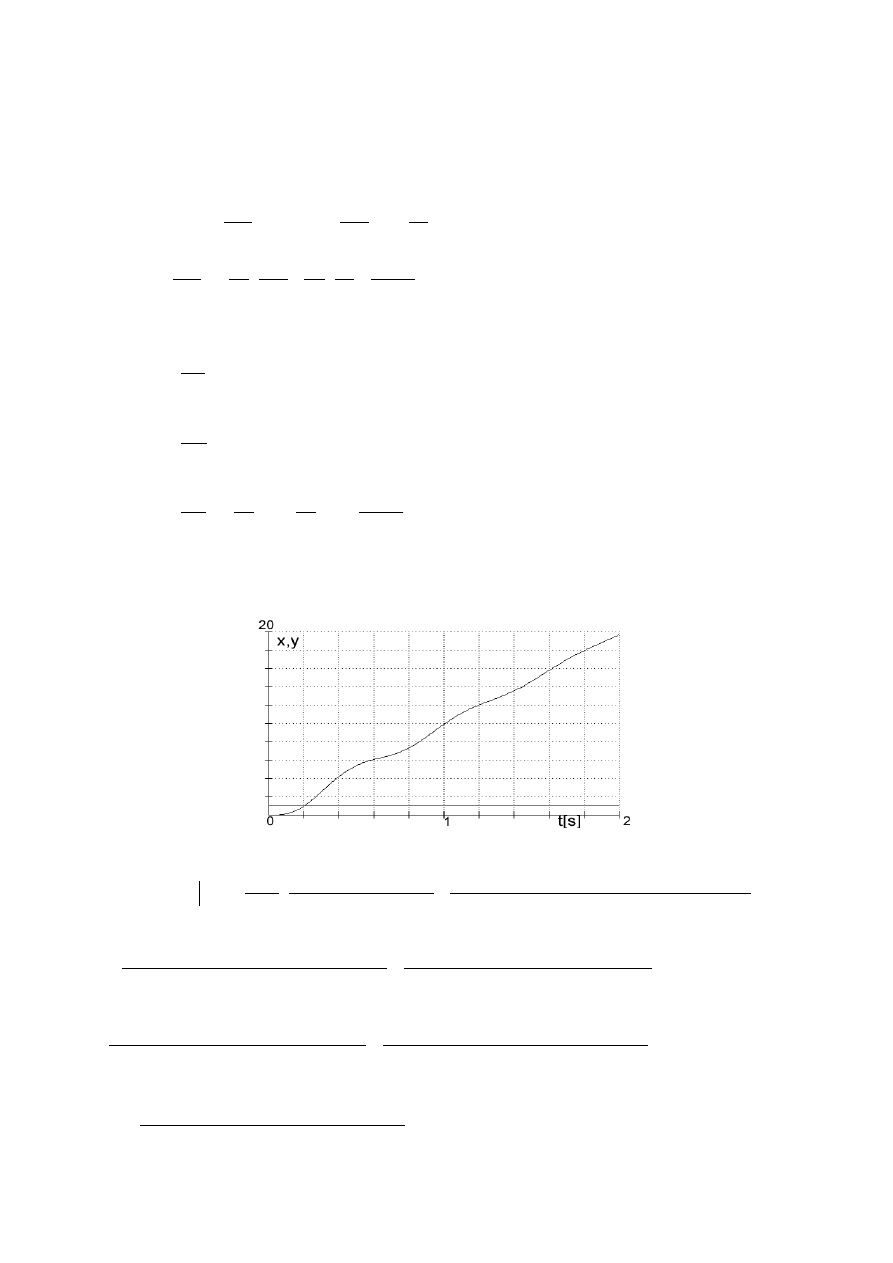
Drugi sposób: numeryczny
(
)
)
(
)
(
2
2
3
2
s
X
k
s
Y
s
T
s
T
T
s
T
T
c
c
c
⋅
=
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
ξ
)
(
2
2
2
3
3
2
t
x
k
dt
dy
T
dt
y
d
T
T
dt
y
d
T
T
c
c
c
⋅
=
⋅
+
⋅
⋅
⋅
+
⋅
⋅
ξ
)
(
1
2
2
2
2
2
3
3
t
x
T
T
k
dt
dy
T
dt
y
d
T
dt
y
d
c
⋅
⋅
+
⋅
−
⋅
−
=
ξ
Wprowadzamy oznaczenie:
i otrzymujemy układ równań:
1
y
y
≡
⎪
⎪
⎪
⎪
⎪
⎩
⎪⎪
⎪
⎪
⎪
⎨
⎧
⋅
⋅
+
⋅
−
⋅
−
=
=
=
)
(
1
2
2
2
2
3
3
3
2
2
1
t
x
T
T
k
y
T
y
T
dt
dy
y
dt
dy
y
dt
dy
c
ξ
Rozwiązując numerycznie powyższy układ równań wyznaczamy odpowiedź szeregowo
połączonych członów całkującego idealnego z oscylacyjnym II-go rzędu na skok
jednostkowy.
Charakterystyka amplitudowo częstotliwościowa A(
ω).
Transmitancja widmowa członu oscylacyjnego II-go rzędu
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
)
(
)
(
1
4
1
1
4
2
1
2
1
2
1
2
2
2
1
2
1
)
(
)
(
2
2
2
2
2
4
2
2
2
2
2
2
2
2
2
2
4
2
2
2
2
2
2
2
2
2
2
2
2
2
3
2
2
2
3
2
2
2
ω
⋅
+
ω
=
ω
⋅
−
⋅
ω
⋅
+
ω
⋅
⋅
⋅
ξ
ω
⋅
−
⋅
ω
⋅
⋅
−
⋅
+
+
ω
⋅
−
⋅
ω
⋅
+
ω
⋅
⋅
⋅
ξ
ω
⋅
⋅
⋅
ξ
⋅
−
=
ω
⋅
−
ω
⋅
⋅
−
ω
⋅
⋅
⋅
ξ
−
ω
⋅
−
⋅
ω
⋅
⋅
−
ω
⋅
⋅
⋅
ξ
−
⋅
ω
⋅
−
ω
⋅
⋅
+
ω
⋅
⋅
⋅
ξ
−
=
ω
⋅
⋅
−
ω
⋅
⋅
+
ω
⋅
⋅
⋅
ξ
−
=
=
ω
⋅
⋅
+
ω
⋅
⋅
⋅
⋅
ξ
+
ω
⋅
⋅
⋅
=
+
⋅
⋅
ξ
+
⋅
⋅
⋅
=
=
ω
ω
=
Q
j
P
T
T
T
T
T
T
k
j
T
T
T
T
T
T
k
T
T
j
T
T
T
T
j
T
T
T
T
j
T
T
k
T
T
T
j
T
T
k
j
T
j
T
T
j
T
T
k
s
T
s
T
k
s
T
s
G
j
G
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
j
s
gdzie:
(
)
2
2
2
2
2
4
2
2
2
2
1
4
2
)
(
ω
⋅
−
⋅
ω
⋅
+
ω
⋅
⋅
⋅
ξ
ω
⋅
⋅
⋅
ξ
⋅
−
=
ω
T
T
T
T
T
T
k
P
c
c
c
składowa rzeczywista transmitancji
widmowej
(
)
(
)
2
2
2
2
2
4
2
2
2
2
2
1
4
1
)
(
ω
⋅
−
⋅
ω
⋅
+
ω
⋅
⋅
⋅
ξ
ω
⋅
−
⋅
ω
⋅
⋅
−
=
ω
T
T
T
T
T
T
k
Q
c
c
c
składowa urojona transmitancji widmowej
( )
(
)
(
)
(
)
(
)
2
2
2
2
2
4
2
2
2
2
2
2
2
2
2
4
2
2
2
2
2
2
2
2
2
2
2
4
2
2
2
2
2
2
1
4
1
4
1
1
4
2
)
(
)
(
)
(
)
(
)
(
)
(
ω
⋅
−
⋅
ω
⋅
+
ω
⋅
⋅
⋅
ξ
=
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ω
⋅
−
⋅
ω
⋅
+
ω
⋅
⋅
⋅
ξ
ω
⋅
−
⋅
ω
⋅
⋅
−
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ω
⋅
−
⋅
ω
⋅
+
ω
⋅
⋅
⋅
ξ
ω
⋅
⋅
⋅
ξ
⋅
−
=
=
ω
+
ω
=
ω
⋅
+
ω
=
ω
=
ω
=
ω
T
T
T
T
k
T
T
T
T
T
T
k
T
T
T
T
T
T
k
Q
P
Q
j
P
j
G
f
A
c
c
c
c
c
c
c
c
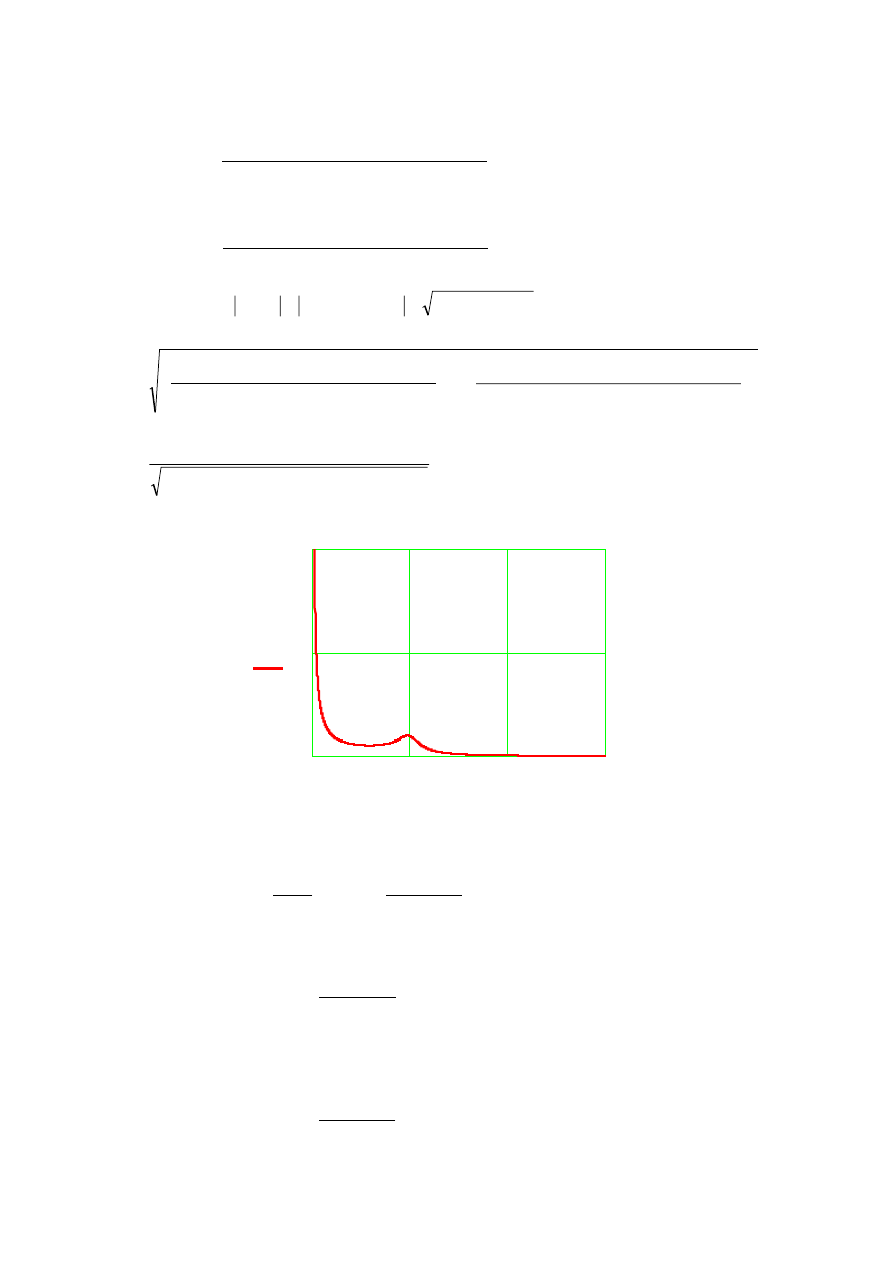
moduł transmitancji widmowej
A
ω
(
)
ω
0
10
20
30
0
50
100
Charakterystyka fazowo częstotliwościowa
( )
ω
ϕ
.
Argument transmitancji widmowej
( )
( )
( )
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
⋅
⋅
−
=
=
ω
ξ
ω
ω
ω
ω
ϕ
T
T
arc
P
Q
arc
2
1
tg
tg
2
2
Dla III ćwiartki w której
0
)
(
0
)
(
<
ω
<
ω
P
i
Q
( )
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
⋅
⋅
−
+
−
=
ω
ξ
ω
π
ω
ϕ
T
T
arc
2
1
tg
2
2
Dla IV ćwiartki w której
0
)
(
0
)
(
<
>
ω
ω
P
i
Q
( )
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
⋅
⋅
−
−
−
=
ω
ξ
ω
π
ω
ϕ
T
T
arc
2
1
tg
2
2
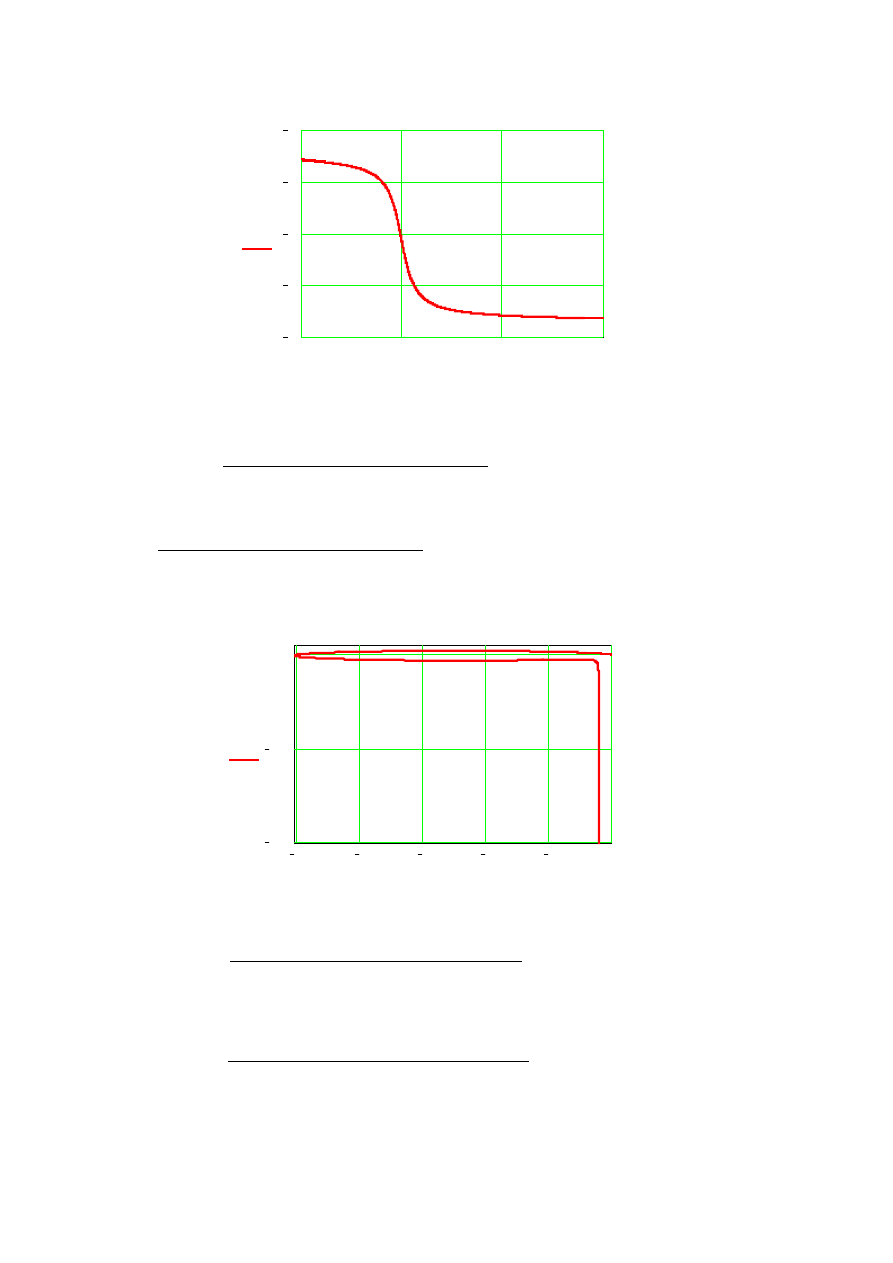
φ ω
(
)
ω
0
10
20
30
5
4
3
2
1
Charakterystyka amplitudowo fazowa (wykres Nyquista).
Składowa urojona transmitancji widmowej
(
)
(
)
2
2
2
2
2
4
2
2
2
2
2
1
4
1
)
(
ω
⋅
−
⋅
ω
⋅
+
ω
⋅
⋅
⋅
ξ
ω
⋅
−
⋅
ω
⋅
⋅
−
=
ω
T
T
T
T
T
T
k
Q
c
c
c
Składowa rzeczywista transmitancji widmowej
(
)
2
2
2
2
2
4
2
2
2
2
1
4
2
)
(
ω
⋅
−
⋅
ω
⋅
+
ω
⋅
⋅
⋅
ξ
ω
⋅
⋅
⋅
ξ
⋅
−
=
ω
T
T
T
T
T
T
k
P
c
c
c
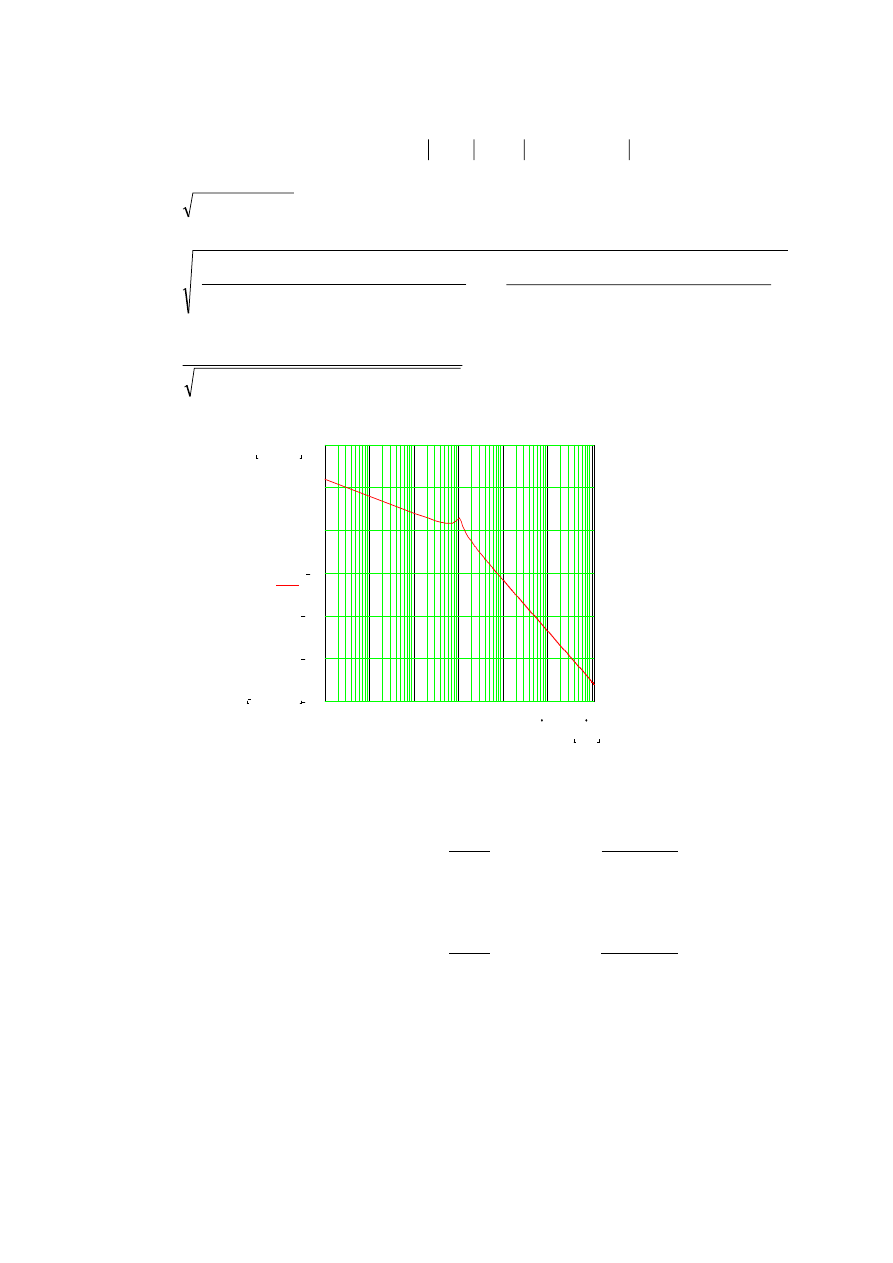
Składowe rzeczywista i urojona transmitancji.
Q
ω
(
)
P
ω
(
)
10
8
6
4
2
0
200
100
0
Składowa rzeczywista transmitancji widmowej
(
)
2
2
2
2
2
4
2
2
2
2
1
4
2
)
(
ω
ω
ω
ξ
ω
ξ
ω
⋅
−
⋅
⋅
+
⋅
⋅
⋅
⋅
⋅
⋅
⋅
−
=
T
T
T
T
T
T
k
P
c
c
c
Składowa urojona transmitancji widmowej
(
)
(
)
2
2
2
2
2
4
2
2
2
2
2
1
4
1
)
(
ω
ω
ω
ξ
ω
ω
ω
⋅
−
⋅
⋅
+
⋅
⋅
⋅
⋅
−
⋅
⋅
⋅
−
=
T
T
T
T
T
T
k
Q
c
c
c
Logarytmiczna charakterystyka amplitudowo częstotliwościowa.
( )
( )
( )
(
)
(
)
(
)
(
)
2
2
2
2
2
4
2
2
2
2
2
2
2
2
2
4
2
2
2
2
2
2
2
2
2
2
2
4
2
2
2
2
2
2
1
1
4
lg
20
1
4
1
1
4
2
lg
20
)
(
)
(
lg
20
)
(
)
(
lg
20
)
(
lg
20
)
(
lg
20
lg
ω
⋅
−
⋅
ω
⋅
+
ω
⋅
⋅
⋅
ξ
=
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ω
⋅
−
⋅
ω
⋅
+
ω
⋅
⋅
⋅
ξ
ω
⋅
−
⋅
ω
⋅
⋅
−
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ω
⋅
−
⋅
ω
⋅
+
ω
⋅
⋅
⋅
ξ
ω
⋅
⋅
⋅
ξ
⋅
−
=
=
ω
+
ω
=
=
ω
⋅
+
ω
=
ω
=
ω
=
ω
=
ω
=
ω
T
T
T
T
k
T
T
T
T
T
T
k
T
T
T
T
T
T
k
Q
P
Q
j
P
j
G
A
M
f
Lm
c
c
c
c
c
c
c
c
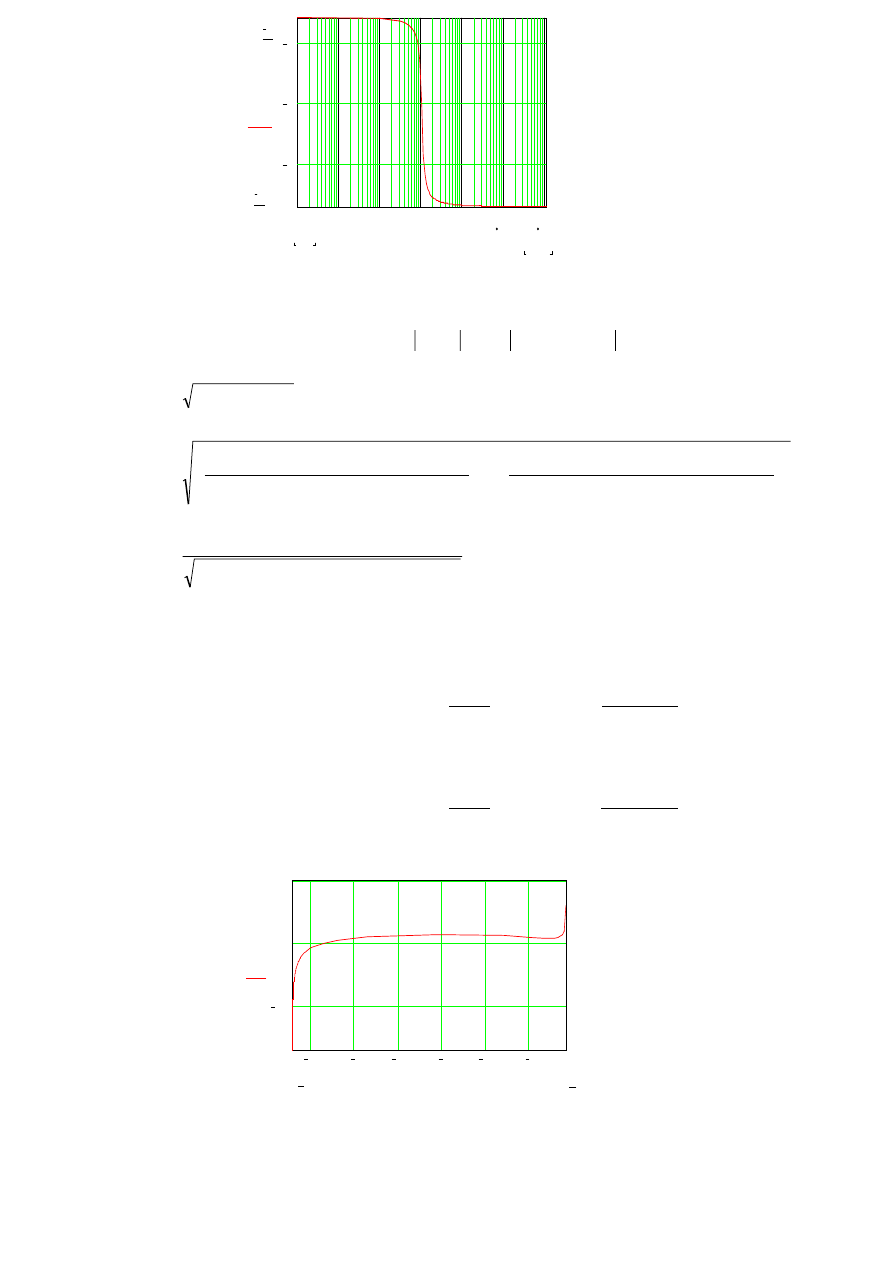
Logarytmiczna charakterystyka fazowo częstotliwościowa.
60.000009
179.999991
L
ω
( )
1 10
4
.
0.01
ω
0.01
0.1
1
10
100
1 10
3
1 10
4
200
150
100
50
0
50
100
Dla III ćwiartki w której
0
)
(
0
)
(
<
ω
<
ω
P
i
Q
( )
( )
( )
[
]
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
⋅
⋅
−
+
−
=
=
=
=
ω
ξ
ω
π
ω
ω
ω
ω
ω
ϕ
T
T
arc
P
Q
arc
j
G
f
2
1
tg
)
(
)
(
tg
arg
lg
2
2
2
Dla IV ćwiartki w której
0
)
(
0
)
(
<
ω
>
ω
P
i
Q
( )
( )
( )
[
]
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
⋅
⋅
−
−
−
=
=
=
=
ω
ξ
ω
π
ω
ω
ω
ω
ω
ϕ
T
T
arc
P
Q
arc
j
G
f
2
1
tg
)
(
)
(
tg
arg
lg
2
2
2
π
2
3
2
π.
φ ω
( )
1 10
4
.
0.01
ω
0.01
0.1
1
10
100 1 10
3
1 10
4
4
3
2
Logarytmiczna charakterystyka amplitudowo fazowa (wykres Blacka).
Logarytmiczna charakterystyka modułu
( )
( )
( )
(
)
(
)
(
)
(
)
2
2
2
2
2
4
2
2
2
2
2
2
2
2
2
4
2
2
2
2
2
2
2
2
2
2
2
4
2
2
2
2
2
2
1
1
4
lg
20
1
4
1
1
4
2
lg
20
)
(
)
(
lg
20
)
(
)
(
lg
20
)
(
lg
20
)
lg(
20
lg
ω
⋅
−
⋅
ω
⋅
+
ω
⋅
⋅
⋅
ξ
=
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ω
⋅
−
⋅
ω
⋅
+
ω
⋅
⋅
⋅
ξ
ω
⋅
−
⋅
ω
⋅
⋅
−
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ω
⋅
−
⋅
ω
⋅
+
ω
⋅
⋅
⋅
ξ
ω
⋅
⋅
⋅
ξ
⋅
−
=
=
ω
+
ω
=
=
ω
⋅
+
ω
=
ω
=
ω
=
ω
=
ω
=
ω
T
T
T
T
k
T
T
T
T
T
T
k
T
T
T
T
T
T
k
Q
P
Q
j
P
j
G
M
f
Lm
c
c
c
c
c
c
c
c
Logarytmiczna charakterystyka fazy
Dla III ćwiartki w której
0
)
(
0
)
(
<
ω
<
ω
P
i
Q
( )
( )
( )
[
]
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
⋅
⋅
−
+
−
=
=
=
=
ω
ξ
ω
π
ω
ω
ω
ω
ω
ϕ
T
T
arc
P
Q
arc
j
G
f
2
1
tg
)
(
)
(
tg
arg
lg
2
2
2
Dla II ćwiartki w której
0
)
(
0
)
(
<
ω
>
ω
P
i
Q
( )
( )
( )
[
]
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
⋅
⋅
−
−
−
=
=
=
=
ω
ξ
ω
π
ω
ω
ω
ω
ω
ϕ
T
T
arc
P
Q
arc
j
G
f
2
1
tg
)
(
)
(
tg
arg
lg
2
2
2
4.5
4
3.5
3
2.5
2
100
0
100
100
170
−
Lm
ω
( )
π
2
−
3
2
− π
⋅
φ ω
( )
Document Outline
- ZAKŁAD MECHATRONIKI
- LABORATORIUM PODSTAW AUTOMATYKI
- Sposób drugi: numeryczny
- Składowa rzeczywista transmitancji widmowej
Wyszukiwarka
Podobne podstrony:
Podstawy automatyki nr 4
Podstawy automatyki nr 1
Podstawy automatyki nr 2
Podstawy automatyki nr 6
Podstawy automatyki nr 4
Podstawy automatyki nr 1
podstawy automatyki ćwiczenia lista nr 4b
podstawy automatyki ćwiczenia lista nr 4c
podstawy automatyki ćwiczenia lista nr 5b
podstawy automatyki ćwiczenia lista nr 3c
podstawy automatyki ćwiczenia lista nr 4d
podstawy automatyki ćwiczenia lista nr 4d
podstawy automatyki ćwiczenia lista nr 5a
podstawy automatyki ćwiczenia lista nr 1b
podstawy automatyki ćwiczenia lista nr 5a
podstawy automatyki ćwiczenia lista nr 4c
podstawy automatyki ćwiczenia lista nr 5b
więcej podobnych podstron