Bryła sztywna 

1. Znajdź moment bezwładności jednorodnego pręta o masie M i długości L względem prostopadłej do pręta osi: 
a) symetralnej 

       

 

  

 

 

       

 

 

         

 

 

 

    

 

 

 
 

 

 
 

   

 

    

 

 

 
 

 

 
 

  

 

 

 

  

 

 
 

 
 

 

 

  

  

 

 

b) przechodzącej przez jeden z kooców pręta 

       

 

  

 

 

       

 

 

         

 

 

 

    

 

 

 

 

   

 

    

 

 

 

 

  

 

 

 

  

 

 

 

 
 

  

 

 

Dynamika ruchu obrotowego 

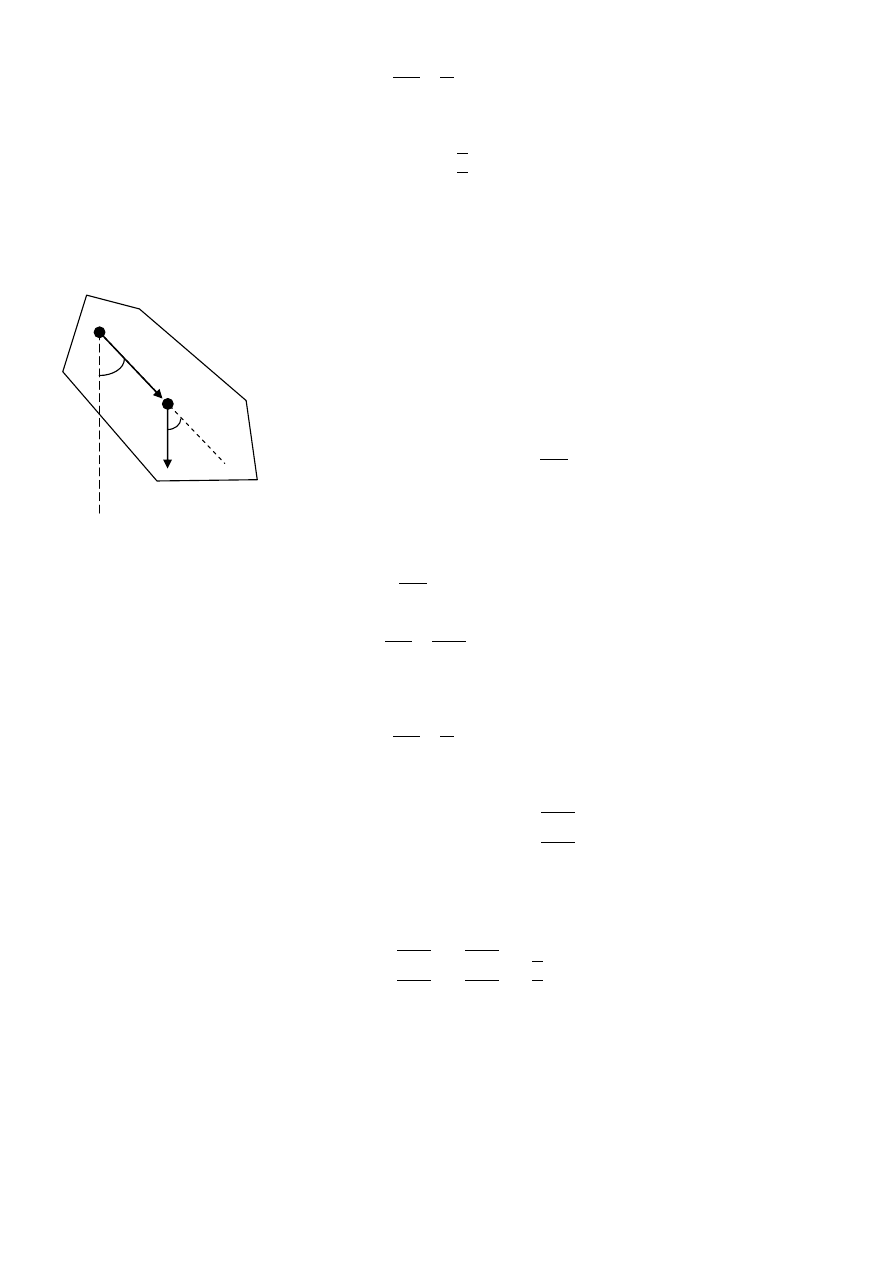
1. Na cząstkę znajdującą się w położeniu określonym wektorem r działa siła F. Znaleźd związek pomiędzy 
momentem pędu cząstki i momentem siły F. Kiedy moment pędu cząstki jest stały? 

Moment siły   wynosi: 

             

Moment pędu cząstki wynosi: 

             

Liczymy pochodną po czasie momentu pędu: 

   

  

 

 

  

           

   

  

           

   

  

                     

Ponieważ              otrzymujemy: 

   

  

                 

Jest to II zasada dynamiki dla ruchu obrotowego. 

Jeśli na cząstkę działa siła   , której moment        (jest równy zeru), to moment pędu tej cząstki jest zachowan: 

   

  

                  

 

                      

Jest to zasada zachowania momentu pędu dla pojedynczej cząstki. 
 
 
 
 
 
 
 
 
 

2. Otrzymad zależnośd między momentem pędu i prędkością kątową obracającej się wokół stałej osi bryły sztywnej 
o momencie bezwładności I. 

Rozpatrujemy obrót wokół osi z. 

Moment pędu masy  

 

: 

  

 

         

 

 

 

 

 

                  

 

 

 

 

 

           

 

  

Ponieważ ruch odbywa się w płaszczyźnie XY, a   

 

 jest prostopadły do płaszczyzny ruchu. 

  

 

   

 

 

 

 

 

            

 

    

 

     

 

 

 

  

 

           

 

 

 

 

         

Całkowity moment pędu bryły: 

        

 

 

 

     

 

 

 

 

               

 

 

 

 

 

          

 

    

  

Ponieważ ruch obrotowy zachodzi tylko wokół osi z: 

                                                   

             

Więc: 

       

3. Z dwóch stron układu dwóch identycznych bloczków o momencie bezwładności I i promieniu R zawieszono na 
bardzo lekkiej lince dwie różne masy m1, m2. Znajdź przyspieszenie mas i siły naprężenia linki. 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

   

 

 

 

 

 

 

 

 

   

 

 

   

 

 

 

 

  

 

 

 

 

 

 

 

  

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

   

 

 

 

 

          

 

     

 

     

 

 

 

 

 

 

 

   

 

 

 

 

       

 

     

 

   

 

  

 

 

 

 

  

 

 

 

 

 

   

 

  

  

. 

. 

          

 

     

 

     

 

                  

 

     

 

      

 

   

 

   

               

 

   

 

   

 

 

 

 

 

                      

 

   

 

         

 

   

 

        

 

   

 

  

                      

 

   

 

        

  

    

 

   

 

       

 

 

      

 

         

 

   

 

     

 

 

 

 

  

 

   

 

         

 

   

 

        

 

 

 

 

  

 

   

 

 

  

 

 

          

 

   

 

    

   

 

 

  

 

 

 

  

 

 

  

  

 

  

           

 

   

 

        

           

 

   

 

        

           

 

   

 

 

  

 

 

 

Gdy zaniedbamy masę bloczków (I=0) 

   

 

 

   

 

 

 

   

 

  

 

Ruch drgający 

1. Rozwiązad równanie ruchu oscylatora harmonicznego prostego z warunkami początkowymi: 
a) x(t=0)=x0 i v(t=0)=0, 
b) x(t=0)=0 i v(t=0)=v0.  
Jaka jest częstośd i amplituda tych drgao? 

             

 

 

 

 

  

 

               

 

 

 

 

  

 

          

Szukamy rozwiązania: 

      

  

 

 

 

 

  

 

   

  

       

  

    

Z równania charakterystycznego: 

  

 

 

 

  

 

 

 

 

 

   

 

  

  

. 

. 

                

 

   

 

   

                 

  

 

        

       

 

 

                     

Rozwiązanie ogólne 

        

 

 

  

 

 

 

   

 

 

   

 

 

 

 

Wprowadźmy oznaczenie:      

 

 

  

 
 

  - częstośd drgao własnych – wtedy: 

        

 

 

   

   

 

 

    

 

Jest to funkcja okresowa o okresie T: 

                       

 

           

  

 

 

Dla warunków początkowych a: 

   

 

     

 

   

 

       

 

      

  

  

      

 

 

   

   

 

 

    

  

 

 

 

 

   

 

   

 

 

    

 

   

 

    

 

 

   

 

   

 

 

    

 

     

  

 

 

 

   

 

 

   

 

        

 

 

   

 

 

    

 

 

 

 

 

 

   

 

 

   

 

 

 

 

   

 

 

   

         

         

             

 

 

   

 

 

 

 

 

 

 

 

 

 

 

 

 

 

    

 

       

 

 

 

 

 

 

   

 

 

        

 

 

   

   

 

 

    

 

 

 

 

 

    

 

 

   

 

 

 

 

 

   

 

 

    

 

 

 

 

  

      

 

 

   

       

 

 

 

   

 

           

 

     

 

            

Gdzie        

 

 jest fazą początkową drgao. Jeśli  

 

    to       i         

 

       

Amplituda      

 

. Częstośd      . 

Dla warunków początkowych b: 

   

 

         

   

 

     

 

  

 

      

  

  

      

 

 

   

   

 

 

    

  

 

 

 

 

   

 

   

 

 

    

 

   

    

 

 

   

 

   

 

 

    

 

     

 

  

 

 

 

   

 

 

   

 

        

 

 

   

 

 

    

 

 

 

 

 

 

 

   

 

 

   

 

 

 

   

 

 

 

 

 

  

         

         

             

 

 

 

 

 

   

        

 

 

   

 

 

   

 

 

 

 

 

 

   

 

    

 

       

 

   

 

 

   

 

   

 

 

        

 

 

   

   

 

 

    

 

 

 

   

 

    

 

 

   

 

 

 

   

 

   

 

 

    

 

 

 

   

  

      

 

 

   

       

 

 

 

   

 

 

 

  

    

       

 

 

   

      

 

 

    

 

 

 

           

 

   

 

 

 

            

Gdzie        

 

 jest fazą początkową drgao. Jeśli  

 

    to       i         

 

       

Amplituda    

 

 

 

. Częstośd      . 

 

2. Policzyd częstośd drgao wahadła matematycznego o masie m i długości l. 

 

 

 

 

 

 

 

 

 

 

  

 

            

Dla małych kątów    

           

 
 

 

 

        

Wtedy równanie ruchu wahadła matematycznego: 

 

 

 

 

  

 

          

 

 

 

  

 

          

                 

 

 

 

 

  

 

          

 

 

 

  

 

 

 

 

       

Jest to równanie ruchu harmonicznego prostego, tzn. 

  

  

  

   

 

 

  

 

 

    

  

 

 

  

 

 

 

 

  

 

    

 

 

 

 

           

Rozważamy małe wychylenia z położenia równowagi, dla których możemy 
przyjąd, że s jest odcinkiem i ruch masy m wzdłuż s pod wpływem działania 
siły   

 

 jest ruchem jednowymiarowym (  

 

 jest styczna do okręgu i jej 

działanie powoduje tylko zmianę długości łuku s). 
Równanie ruchu masy m: 

 

 

 

 

  

 

 

 

 

       

Czyli rozwiązanie: 

     

 

                           

 

 

                                

 

3. Policzyd częstośd drgao wahadła fizycznego o masie m i momencie bezwładności I zawieszonego w odległości d 
od środka masy. 

 

 

 

 

 

 

 

 

 

 

 

  

 

        

 

 

 

  

 

 

   

 

      

Jest to równanie ruchu harmonicznego prostego, tzn. 

 

 

 

  

 

 

 

 

       

Czyli rozwiązanie: 

     

 

                           

   

 

 

Wahadło matematyczne jest specjalnym przypadkiem wahadła fizycznego. Dla wahadła matematycznego mamy 
      

 

 i otrzymujemy: 

     

   

 

   

   

  

 

   

 
 

 

 

 

 

 

  

  

   

  

   

    

       

              

                                     

   

 

 

 

  

 

 

Ruch obrotowy wokół stałej osi 0 (ruch jednowymiarowy) 

Ma znak dodatni gdy moment siły powodujący to przyspieszenie  
prowadzi do ruchu przeciwnego do ruchu wskazówek zegara. 

4. Napisad równanie ruchu oscylatora tłumionego. Podad przybliżony wzór rozwiązania dla bardzo słabego 
tłumienia drgao i przedstawid to rozwiązanie na rysunku. 

      

 

   

 

 

 

 

        - siła harmoniczna (wymuszająca drgania) 

 

 

    

  

  

         - siła tłumiąca (siła oporu ośrodka) 

v – prędkośd, b>0 

      

 

   

 

    

 

 

 

 

  

 

   

  

  

         

Równanie charakterystyczne: 

  

 

             

     

 

      

 

   

 

       

 

     

  

   

 

  

 

  
  

  

 

  

 

 

 

 

 

   

 

  

    

 

  

 

 

 

 

 

 

Dla 

 

  

   

 

 

      

 

      

   

                  - ruch nie jest ruchem drgajacym 

Ruch drgający otrzymujemy tylko dla 

 

  

   

 

 

   

 

                              

Mamy wtedy: 

  

 

  

 

 

 

 

 

    

 

 

   

 

  

 

 

                   

 

 

   

 

  

 

 

                              

Rozwiązanie ogólne równania ruchu drgającego tłumionego: 

        

 

 

 

 

 

   

 

 

 

 

 

   

 

 

  

 

  

     

   

 

 

  

 

  

     

   

 

  

  

  

 

 

   

   

 

 

    

  

Dla             

 

                  

 

  

   

 

 

   

 

 otrzymujemy: 

      

  

  

   

 

 

    

 

 

   

   

 

 

    

  

 

 

 

  

 

  

  

 

 

   

 

   

 

 

    

 

     

 

  

 

  

      

 

 

   

 

    

 

  

      

 

 

    

 

   

  

 

 

 

  

 

  

  

 

 

   

 

   

 

 

    

 

     

 

 

 

  

  

 

 

   

 

   

 

 

    

 

        

 

 

   

 

    

 

 

    

 

     

  

 

  

   

 

 

    

 

     

 

  

    

 

 

 

 

   

 

   

 

 

    

 

   

 

    

 

 

   

 

    

 

 

    

 

     

  

 

 

 

   

 

 

   

 

        

 

 

   

 

 

    

 

 

 

 

 

 

   

 

 

   

 

 

 

 

   

 

 

             

         

         

             

 

 

   

 

 

 

 

 

 

 

 

 

 

 

 

 

 

    

 

       

 

 

 

 

 

 

   

 

 

        

 

  

  

  

 

 

   

   

 

 

    

     

 

  

  

 

 

 

 

 

    

 

 

   

 

 

 

 

 

   

 

 

    

     

 

  

  

 

 

 

 

  

      

 

 

   

       

 

 

  

   

 

 

 

  

  

           

 

     

 

 

 

  

  

            

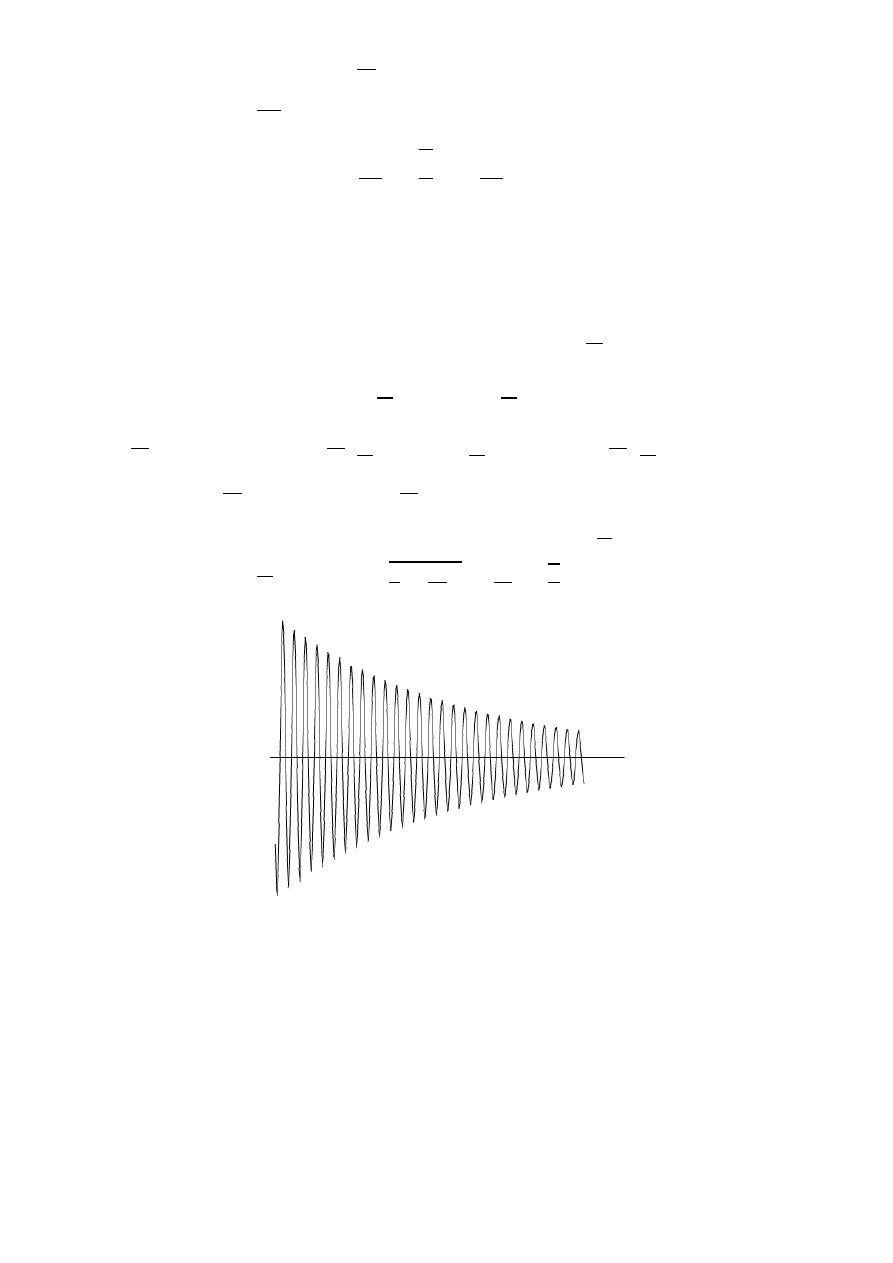
Gdzie        

 

 jest fazą początkową drgao. Jeśli  

 

    to       i         

 

 

 

  

  

       

Amplituda malejąca      

 

 

 

  

  

. Częstośd      

 

 

   

 

  

 

 

 dla  

 

  

   

 

 

 

       

 

 

 

 

 

 

 

 

 

5. Rozwiązad równanie oscylatora harmonicznego prostego z siłą wymuszającą F=Acos(wt) i warunkami 
początkowymi x(t=0)=x0, v(t=0)=0. Kiedy zachodzi rezonans? Znaleźd zależnośd amplitudy drgao rezonansowych 
od czasu. 

Z warunków zadania mamy: 

 

 

 

 

  

 

                 

 

 

 

  

 

   

 

 

              

Gdzie  

 

 

 

 

 

       

 

 

. 

Rozwiązujemy niejednorodne równanie różniczkowe drugiego rzędu: 

 

 

 

  

 

   

 

 

    

        

 

 

  

 

 

   

 

 

   

 

 

   

 

     

 

      

 

     

 

   

                 

 

 

  

 

               

 

 

                        

   

 

            

 

 

                    

   

 

 

 

 

   

 

 

      

 

 

 

 

   

 

        

        

 

     

 

      

 

     

 

    

 

 

 

 

   

 

        

Podstawiając warunki początkowe: 

            

 

 

 

 

 

 

   

 

   

 

       

           

              

 

   

 

 

 

 

 

 

   

 

 

      

  

  

    

 

 

 

     

 

     

 

 

 

     

 

    

 

 

 

 

   

 

          

            

 

 

 

          

           

              

 

    

         

 

 

 

 

 

 

   

 

       

 

    

 

 

 

 

   

 

        

Dla      

 

 

   

   

 

        

 

     

 

        

   

 

 

 

 

 

   

 

                

 

   

   

 

     

 

        

   

 

 

 

 

   

               

 

  

 

 

   

   

 

     

 

    

 

  

 

 

  

         

   

 

   

 

     

 

    

 

  

 

         

 

       

 

     

 

    

  

  

 

     

 

      

 

     

 

      

 

    

 

 

 

 

 

 

 

 

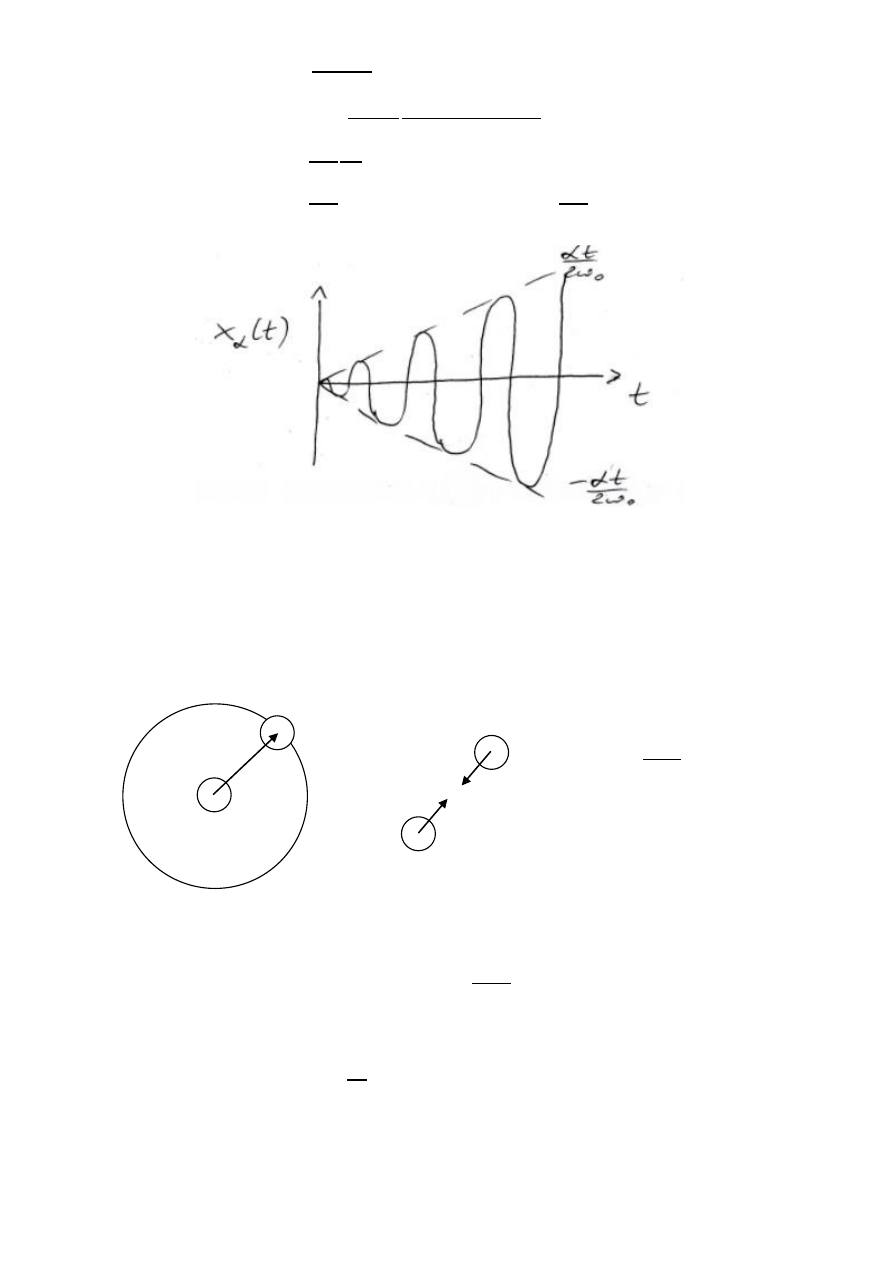
Rezonans zachodzi dla częstości siły wymuszonej równej częstości własnej drgao układu. Amplituda drgao rośnie 
liniowo z czasem. Gdy czas dąży do nieskooczoności to amplituda też. 

Grawitacja 

1. Wyprowadzid drugie prawo Keplera. 

 

 

 

 

 

 

Liczymy moment siły grawitacji działającej na Ziemię : 

                      

   

 

 

        

Wiemy, że: 

    

   

  

           

            

                          

Jest to II prawo Keplera: 

Moment pędu planety poruszającej się wokół słooca jest stały. 

S 

S 

Z 

Z 

   

   

    

      

   

 

 

   

    masa Ziemi 

    masa Słooca