Józef Szymczak
Pochodna funkcji – zastosowania do badania funkcji jednej zmiennej
(notatki z wykładu)
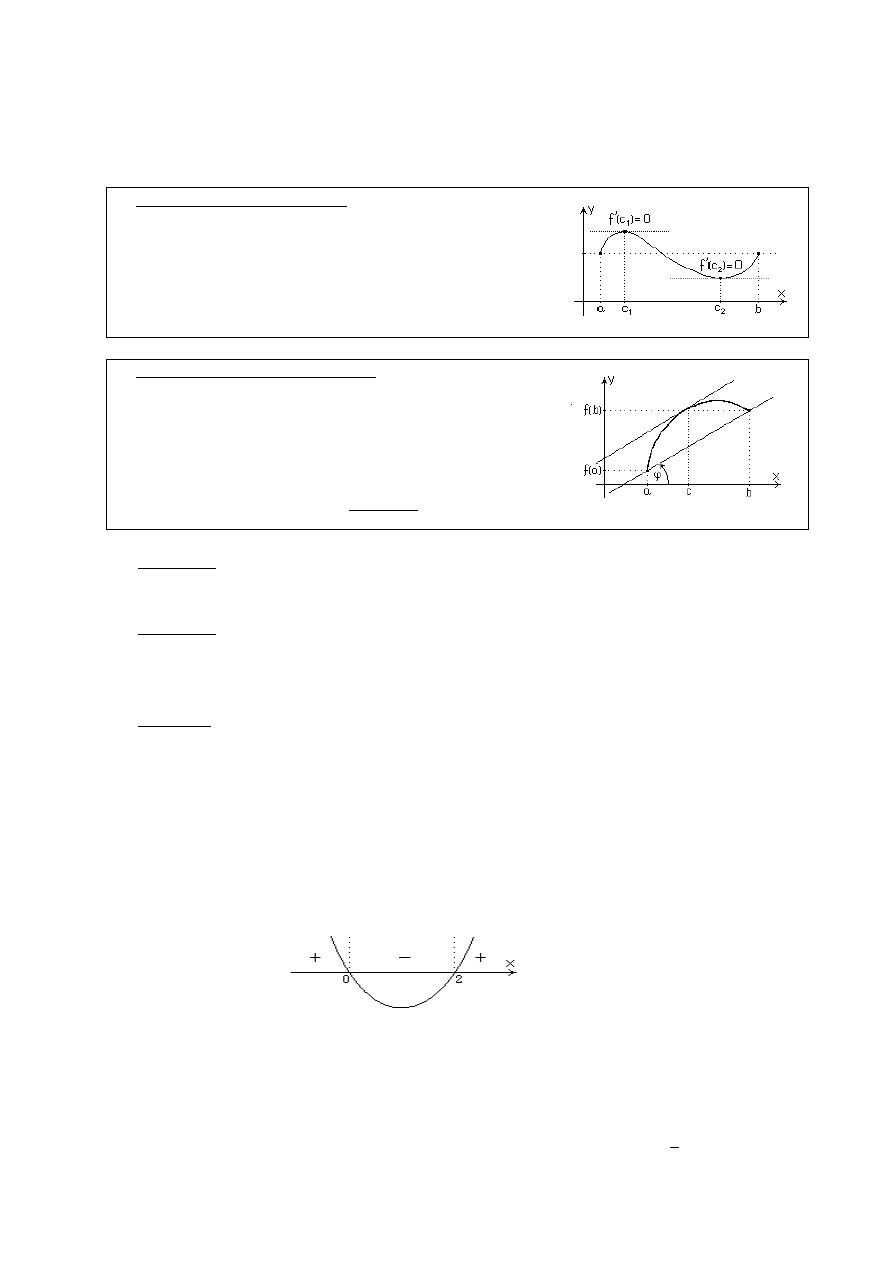
Twierdzenie (1) (tw. Rolle’a).
Jeżeli
)
(x
f
jest funkcją ciągłą na przedziale domkniętym
]
;
[ b
a
, różniczkowalną wewnątrz tego przedziału i
)
(
)
(
b
f
a
f
, to istnieje taki punkt
)
;
( b
a
c
, że
0
)
(
c
f
.
Twierdzenie (2) (tw. Lagrange’a).
Jeżeli
)
(x
f
jest funkcją ciągłą na przedziale domkniętym
]
;
[ b
a
i różniczkowalną wewnątrz tego przedziału, to istnieje
taki punkt
)
;
( b
a
c
, że
)
)(
(
)
(
)
(
a
b
c
f
a
f
b
f
.
(Możemy też zapisać, że
tg
a
b
a
f
b
f
c
f
)
(
)
(
)
(
).
Wniosek 1.
Jeżeli
0
)
(
x
f
dla każdego
)
;
( b
a
x
, to funkcja
)
(x
f
jest stała w przedziale
)
;
( b
a
.
Wniosek 2.
Jeżeli
0
)
(
x
f
dla każdego
)
;
( b
a
x
, to funkcja
)
(x
f
jest rosnąca w tym przedziale; jeżeli
natomiast
0
)
(
x
f
dla każdego
)
;
( b
a
x
, to funkcja
)
(x
f
jest malejąca w tym przedziale.
Przykłady.
a) Określić przedziały monotoniczności funkcji
3
3
)
(
2
3
x
x
x
f
.
Wyznaczymy pochodną danej funkcji i miejsca zerowe pochodnej:
x
x
x
f
6
3
)
(
2
;
2
0
0
)
2
(
3
0
)
(
x
x
x
x
x
f
.
Analizujemy znak pochodnej, wykorzystując do tego metodę graficzną (najwygodniej). Na
tle osi liczbowej kreślimy przebieg czynników występujących w pochodnej i stąd łatwo
oszacować znak pochodnej w poszczególnych przedziałach. W tym przypadku pochodna jest
wyrażona za pomocą wielomianu stopnia drugiego, którego wykresem jest parabola:
Widzimy, że
)
2
;
0
(
0
)
(
x
x
f
oraz
)
;
2
(
)
0
;
(
0
)
(
x
x
f
. Stąd wniosek, że
)
(x
f
jest malejąca w przedziale
)
2
;
0
(
natomiast jest rosnąca w przedziałach:
)
0
;
(
,
)
;
2
(
(ale nie na sumie tych przedziałów!).
b) Określić przedziały monotoniczności funkcji
x
x
x
f
ln
)
(
.
Mamy tu
)
;
0
(
f
D
,
1
ln
)
(
x
x
f
,
e
e
x
x
x
f
1
1
ln
0
)
(
1
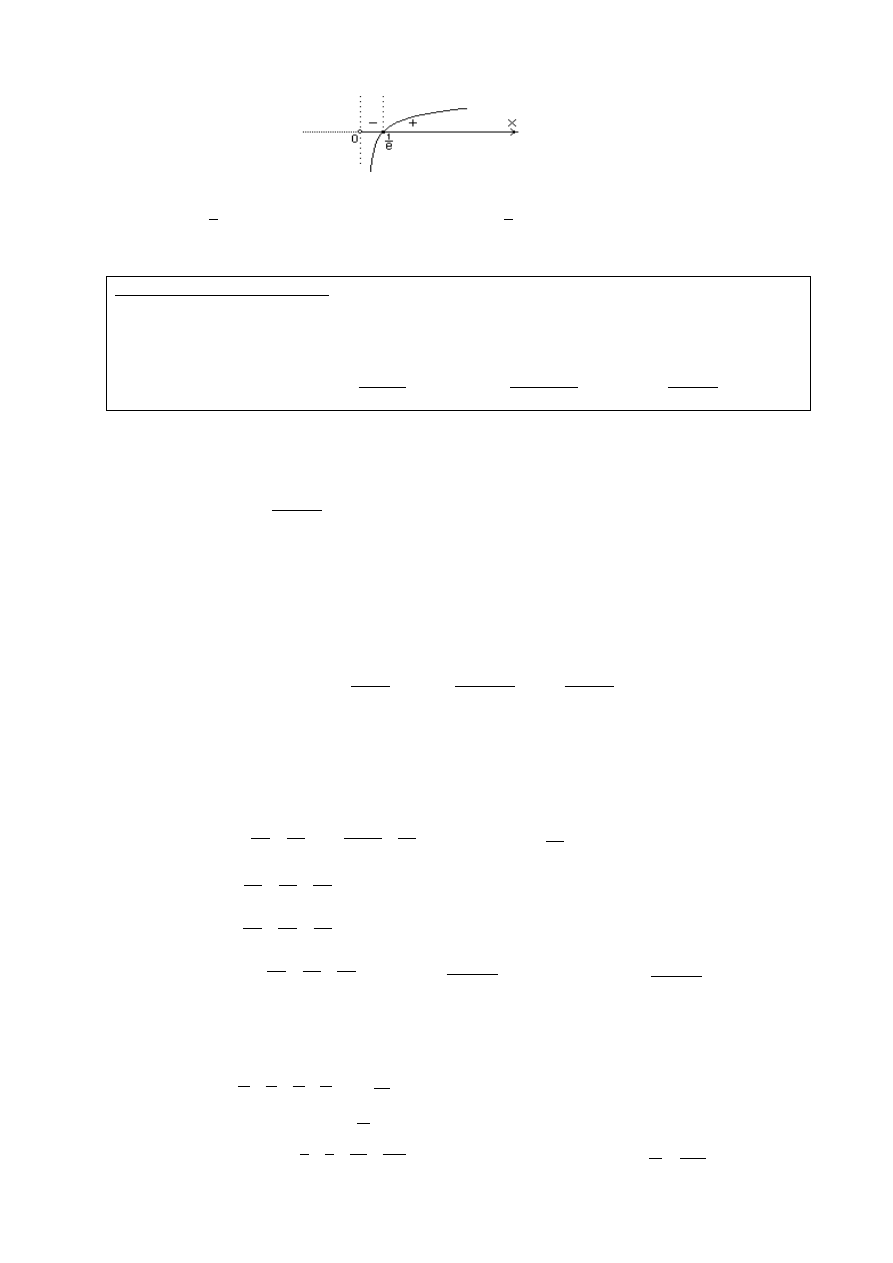
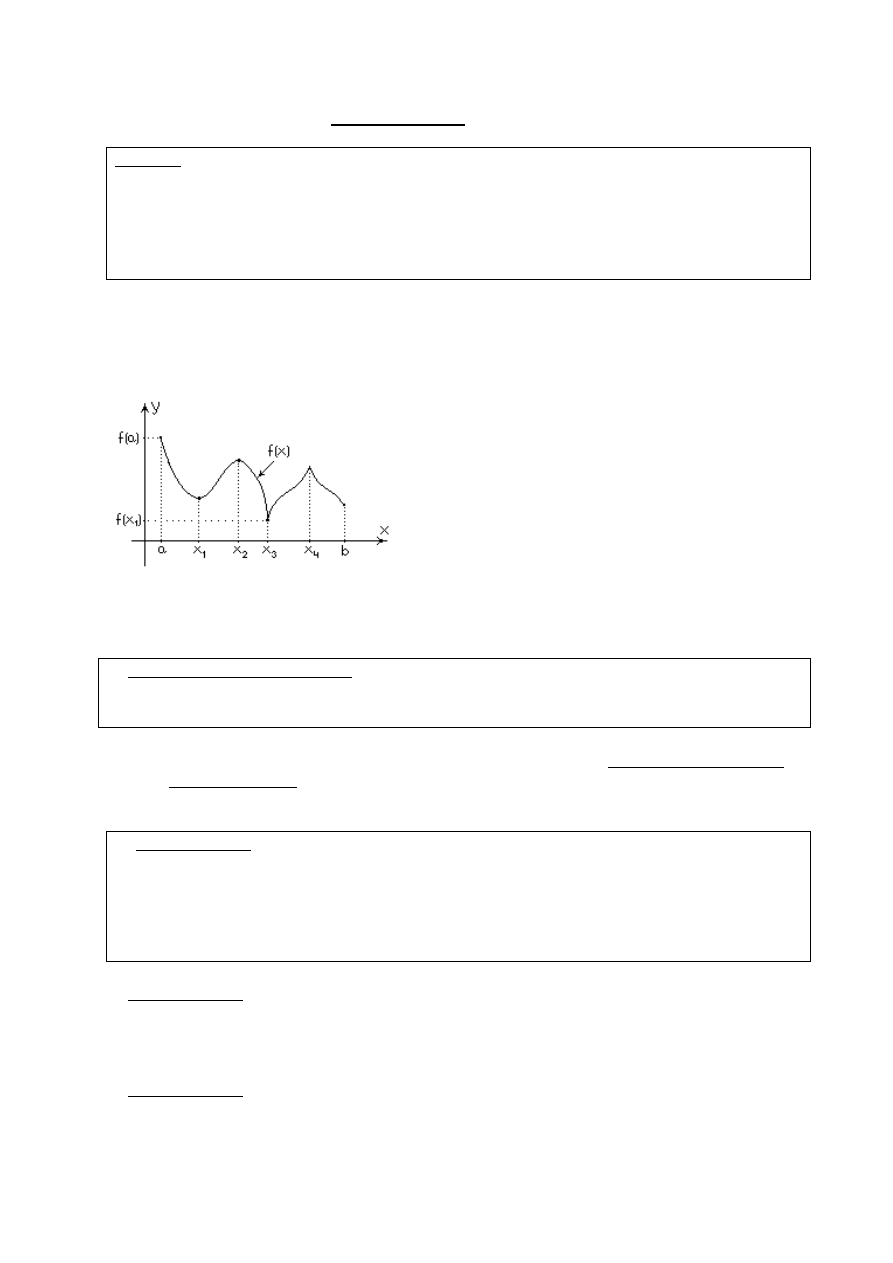
Na podstawie pomocniczego wykresu pochodnej możemy stwierdzić, że
)
(x
f
jest malejąca w
przedziale
)
1
;
0
(
e , natomiast jest rosnąca w przedziale
)
;
1
(
e
.
Twierdzenie (3) (tw. Taylora).
Jeżeli
)
(x
f
jest n-krotnie różniczkowalna w pewnym otoczeniu
)
;
(
0
x
U
, to dla każdego
)
;
(
0
x
S
x
istnieje taki punkt
c
leżący między
0
x i
x
, że
(*)
n
n
x
x
n
c
f
x
x
n
x
f
x
x
x
f
x
x
x
f
x
f
x
f
n
n
)
(
!
)
(
)
(
1)!
(
)
(
...
)
(
!
2
)
(
)
)(
(
)
(
)
(
0
)
(
0
0
)
1
(
2
0
0
0
0
0
1
.
Wzór (*) nazywamy wzorem Taylora. Ostatni składnik nazywamy n-tą resztą wzoru Taylora
i oznaczamy symbolem
n
R
:
n
x
x
n
c
f
n
n
R
)
(
!
)
(
0
)
(
.
W przypadku, gdy
1
n
, wzór Taylora redukuje się do wzoru z twierdzenia Lagrange’a:
)
)(
(
)
(
)
(
0
0
x
x
c
f
x
f
x
f
.
Jeżeli
0
0
x
, to otrzymujemy wzór Taylora o środku w tym punkcie (zwany też wzorem
Mac Laurina):
(**)
n
n
x
n
c
f
x
n
f
x
f
x
f
f
x
f
n
n
!
)
(
)!
1
(
)
0
(
...
!
2
)
0
(
)
0
(
)
0
(
)
(
)
(
)
1
(
2
1
,
a c jest liczbą zawartą między x i 0.
Wzór Taylora służy do przybliżonego przedstawiania wartości funkcji różniczkowalnych za
pomocą wielomianu odpowiednio wysokiego stopnia.
Oto wzory Tylora dla niektórych funkcji:
n
c
x
x
e
x
x
x
x
e
n
n
n
!
)!
1
(
!
3
!
2
1
3
2
...
1
, (tu
n
c
x
e
R
n
n
!
),
n
R
x
x
x
x
x
...
sin
!
7
!
5
!
3
7
5
3
,
n
R
x
x
x
x
...
1
cos
!
6
!
4
!
2
6
4
2
,
n
n
c
n
x
x
x
x
x
x
n
)
1
(
)
1
(
...
)
1
ln(
1
4
3
2
4
3
2
, (tu
n
n
n
c
n
x
R
n
)
1
(
)
1
(
1
).
Szacując wartość n-tej reszty wzoru Taylora możemy z dowolną dokładnością podać
przybliżoną wartość funkcji w danym punkcie x.
Na przykład
n
c
x
n
e
e
e
!
...
1
1
!
5
1
!
4
1
!
3
1
!
2
1
1
,
a ponieważ
)
1
;
0
(
c
więc
!
3
n
R
n
(bo
3
e
), zatem uwzględniając tylko pierwszych sześć
wyrazów mamy:
120
1
24
1
6
1
2
1
1
1
e
z błędem nie przekraczającym
00357
,
0
840
3
!
7
3
.
Ekstrema funkcji (maksima i minima)
Definicja.
Funkcja
)
(x
f
określona w pewnym otoczeniu
)
;
(
0
x
U
ma w punkcie
0
x ,
a) minimum lokalne właściwe
))
(
)
(
)
;
(
(
:
0
0
x
f
x
f
x
S
x
x
b) maksimum lokalne właściwe
))
(
)
(
)
;
(
(
:
0
0
x
f
x
f
x
S
x
x
Maksima i minima nazywamy ekstremami. Są to pojęcia lokalne odnoszące się do
dostatecznie małego otoczenia punktu
0
x
i nie należy ich mylić z pojęciami: wartość największa,
wartość najmniejsza funkcji w pewnym zbiorze.
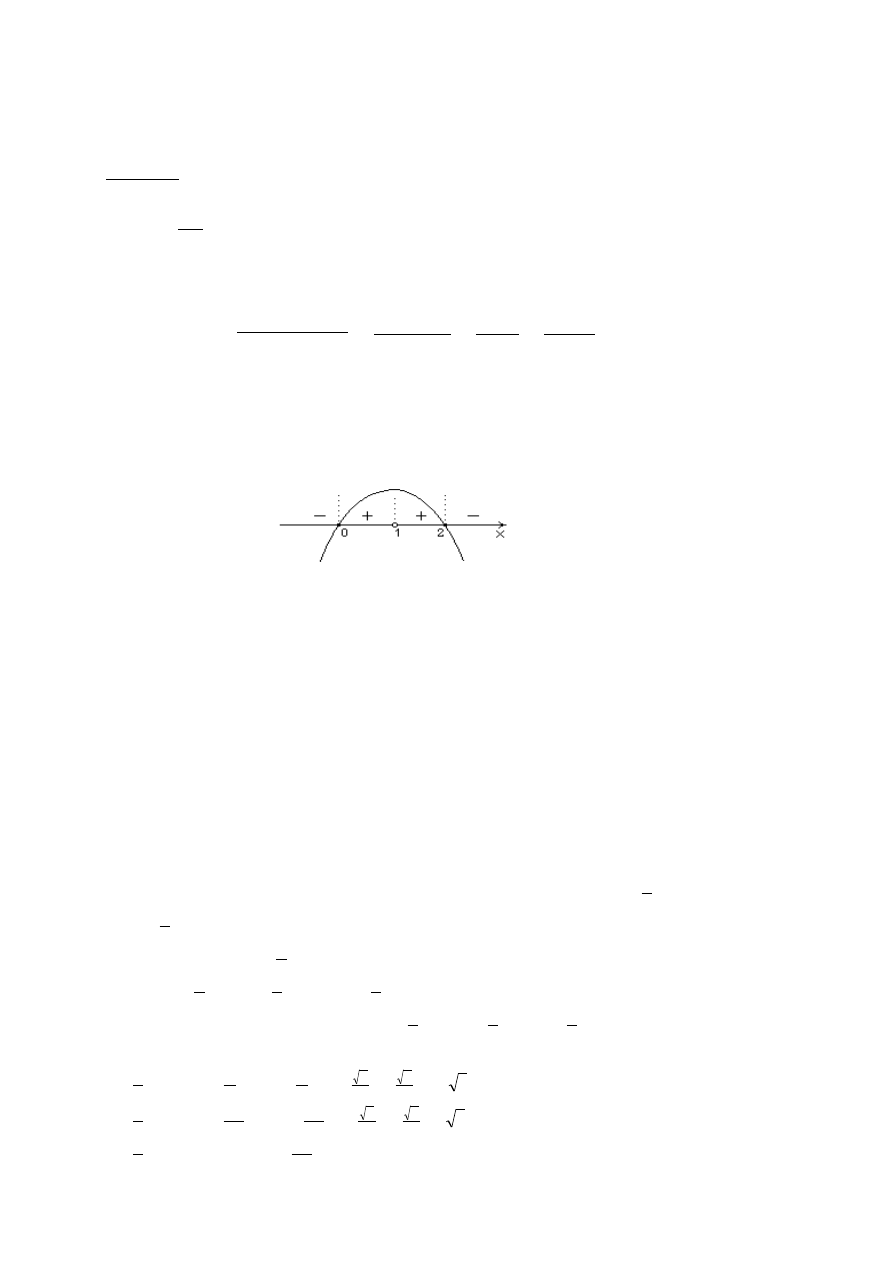
Dla argumentów
3
1
i
x
x
funkcja ma minima
lokalne. Dla argumentów
4
2
i
x
x
funkcja ma
maksima lokalne.
)
(a
f
jest wartością największą funkcji
)
(x
f
w
przedziale
]
;
[ b
a
.
)
(
3
x
f
jest wartością najmniejszą funkcji
)
(x
f
w
przedziale
]
;
[ b
a
.
Zauważmy też, że
0
)
(
1
x
f
,
0
)
(
2
x
f
,
)
(
3
x
f
nie istnieje,
)
(
4
x
f
nie istnieje.
Twierdzenie (4) (tw. Fermata) (warunek konieczny istnienia ekstremum funkcji różniczko-
walnej)
Jeżeli istnieje
)
(
0
x
f
i jeżeli funkcja
)
(x
f
ma w punkcie
))
(
,
(
0
0
x
f
x
ekstremum, to
0
)
(
0
x
f
.
Punkty, w których pochodna funkcji jest równa zero, nazywamy punktami stacjonarnymi tej
funkcji. Punkty krytyczne funkcji, to punkty stacjonarne lub punkty, w których funkcja ciągła
nie ma pochodnej.
Twierdzenie (5) (warunek wystarczający istnienia ekstremum funkcji ciągłej).
Jeżeli funkcja
)
(x
f
jest ciągła w punkcie
0
x , a ponadto różniczkowalna w pewnym
sąsiedztwie
)
,
(
0
x
S
, przy czym
0
)
(
x
f
dla
0
x
x
oraz
0
)
(
x
f
dla
0
x
x
, to w punkcie
0
x funkcja ma minimum lokalne właściwe; jeśli natomiast
0
)
(
x
f
dla
0
x
x
i
0
)
(
x
f
dla
0
x
x
, to w punkcie
0
x funkcja ma maksimum lokalne właściwe.
Twierdzenie (6)
Jeżeli
0
)
(
0
x
f
i
0
)
(
0
x
f
, to w punkcie
0
x funkcja ma maksimum lokalne w przypadku
gdy
0
)
(
0
x
f
, natomiast minimum lokalne w przypadku gdy
0
)
(
0
x
f
.
Twierdzenie (7)
Jeżeli
)
(x
f
ma n-tą pochodną w punkcie
0
x , przy czym
0
)
(
...
)
(
)
(
0
)
1
(
0
0
x
x
x
n
f
f
f
i
0
)
(
0
)
(
x
n
f
, a ponadto n jest liczbą parzystą, to w punkcie
0
x funkcja ma maksimum lokalne
jeżeli
0
)
(
0
)
(
x
n
f
, natomiast minimum lokalne jeżeli
0
)
(
0
)
(
x
n
f
. Gdy n jest liczbą nieparzystą,
to w punkcie
0
x funkcja nie ma ekstremum.
Przykłady.
Określić ekstrema lokalne funkcji:
a)
x
x
x
f
1
)
(
2
, b)
3
)
5
(
)
(
x
x
f
, c)
x
x
x
f
cos
2
2
sin
)
(
dla
)
2
;
0
(
x
.
Ad a) Zauważmy, że
)
;
1
(
)
1
;
(
f
D
. Wyznaczamy pochodną danej funkcji i miejsca
zerowe pochodnej (punkty stacjonarne):
2
2
)
1
(
)
1
(
)
1
(
2
)
(
x
x
x
x
x
f
=
2
2
2
)
1
(
2
2
x
x
x
x
=
2
2
)
1
(
2
x
x
x
=
2
)
1
(
)
2
(
x
x
x
;
2
0
0
)
2
(
0
)
(
x
x
x
x
x
f
.
Po przeanalizowaniu znaku pochodnej (wykonać to metodą graficzną), zauważamy, że
)
(x
f
jest
malejąca w przedziałach:
)
0
;
(
,
)
;
2
(
, natomiast jest rosnąca w przedziałach:
)
1
;
0
(
,
)
2
;
1
(
.
Zatem badana funkcja ma minimum lokalne dla
0
x
o wartości 0 oraz ma maksimum lokalne
dla
2
x
o wartości
4
. Zapisuje się to symbolicznie:
0
)
0
(
min
f
,
4
)
2
(
max
f
.
Ad b)
3
)
5
(
)
(
x
x
f
.
Zauważmy, że
2
)
5
(
3
)
(
x
x
f
. Mamy dalej, że
5
0
)
(
x
x
f
(jest to punkt stacjonarny).
Ale widzimy, że
0
)
(
x
f
dla
5
x
, a także
0
)
(
x
f
dla
5
x
. Pochodna nie zmianie znaku
przy przejściu przez punkt stacjonarny (funkcja jest rosnąca dla
5
x
oraz jest rosnąca dla
5
x
), więc dla
5
x
funkcja nie ma ekstremum.
Ad c)
x
x
x
f
cos
2
2
sin
)
(
w przedziale
)
2
;
0
(
. Posłużymy się tu twierdzeniem (6).
Obliczamy pochodną:
.
2
sin
2
sin
4
sin
2
)
sin
sin
1
(
2
sin
2
)
sin
(cos
2
sin
2
2
cos
2
)
(
2
2
2
2
2
x
x
x
x
x
x
x
x
x
x
x
f
Wyznaczając miejsca zerowe pochodnej zastosujemy podstawienie
t
x
sin
i otrzymujemy
równanie
0
2
2
4
2
t
t
, które ma dwa pierwiastki:
1
t
oraz
2
1
t
. Stąd
1
sin
x
lub
2
1
sin
x
. Uwzględniając warunek, że
)
2
;
0
(
x
, mamy:
jeśli
1
sin
x
, to
2
3
x
,
jeśli
2
1
sin
x
, to
6
1
x
lub
6
5
x
.
Są zatem trzy punkty stacjonarne:
6
1
x
,
6
5
x
,
2
3
x
. Wyznaczymy teraz drugą
pochodną badanej funkcji:
x
x
x
f
cos
2
2
sin
4
)
(
.
0
3
3
2
3
2
2
3
4
)
6
cos(
2
)
3
sin(
4
)
6
1
(
f
,
0
3
3
2
3
2
2
3
4
)
6
5
cos(
2
)
3
5
sin(
4
)
6
5
(
f
,
0
0
2
0
4
)
2
3
cos(
2
3
sin
4
)
2
3
(
f
.

Uwzględniając znak drugiej pochodnej w punktach stacjonarnych, określamy ekstrema:
2
3
3
)
6
cos(
2
)
3
sin(
)
6
1
(
max
f
,
2
3
3
)
6
5
cos(
2
)
3
5
sin(
)
6
5
(
min
f
, natomiast w
punkcie
2
3
x
funkcja nie ma ekstremum (sprawdzić, że
0
)
2
3
(
f
).
Zadanie. Wykazać, że spośród wszystkich prostokątów mających taki sam obwód k, największe
pole powierzchni ma kwadrat.
Wiadomo, że
y
x
k
2
2
, skąd
x
k
y
2
. Pole prostokąta
y
x
p
zapiszemy wzorem:
2
2
)
2
(
)
(
x
x
k
x
k
x
x
p
jako funkcję zależną od x.
Wyznaczając pochodną tej funkcji, mamy
x
k
x
p
2
2
)
(
.
4
0
2
2
0
)
(
k
x
x
k
x
p
. W tym punkcie funkcja opisująca pole może mieć ekstremum.
Z kolei otrzymujemy, że
2
)
(
x
p
, więc też
0
2
)
4
(
k
p
, a to oznacza, że dla
4
k
x
jest
maksimum. Przy tym wtedy
x
k
k
k
y
2
4
2
, a więc taki prostokąt o maksymalnym polu jest
kwadratem.
Wyznaczanie wartości największej i najmniejszej funkcji ciągłej na przedziale domkniętym
Wartości te (zwane też ekstremami globalnymi) dla ciągłej funkcji
)
(x
f
, gdzie
b
x
a
,
mogą znajdować się na końcach przedziału lub w tych punktach przedziału
)
;
(
b
a
, w których
funkcja
)
(x
f
osiąga ekstrema.
Aby znaleźć te wartości, obliczamy pochodną funkcji i wyznaczamy punkty stacjonarne oraz
punkty, w których pochodna może nie istnieć (punkty te wraz z punktami stacjonarnymi
nazywamy punktami krytycznymi). Następnie obliczamy wartości funkcji we wszystkich
punktach krytycznych, a także wartości funkcji na końcach przedziału.
Porównujemy otrzymane wartości i wybieramy największą i najmniejszą z nich Wartości te
można oznaczać symbolicznie:
)
(
max
]
;
[
x
f
b
a
,
)
(
min
]
;
[
x
f
b
a
.
Przykład. Wyznaczyć wartość największą i najmniejszą funkcji
2
1
)
(
x
x
x
f
na przedziale
]
3
;
1
[
.
3
4
4
2
4
2
2
)
2
(
2
2
)
1
(
)
(
x
x
x
x
x
x
x
x
x
x
x
x
x
f
.
0
)
(
x
f
dla
2
x
(
)
3
;
1
(
2
).
4
1
2
2
1
)
2
(
2
f
,
0
1
1
1
)
1
(
2
f
,
9
2
3
3
1
)
3
(
2
f
.
Z porównania trzech obliczonych wartości widzimy, że
0
)
(
max
]
3
;
1
[
x
f
,
4
1
)
(
min
]
3
;
1
[
x
f
.
Rodzaje wypukłości funkcji.
Funkcja
)
(x
f
jest wypukła w dół na przedziale
f
D
I
, jeżeli każdy odcinek łączący dwa
dowolne punkty wykresu tej funkcji leży ponad wykresem lub się z nim pokrywa.
Funkcja
)
(x
f
jest ściśle wypukła w dół na przedziale
f
D
I
, jeżeli każdy odcinek łączący
dwa dowolne punkty wykresu tej funkcji leży ponad wykresem.
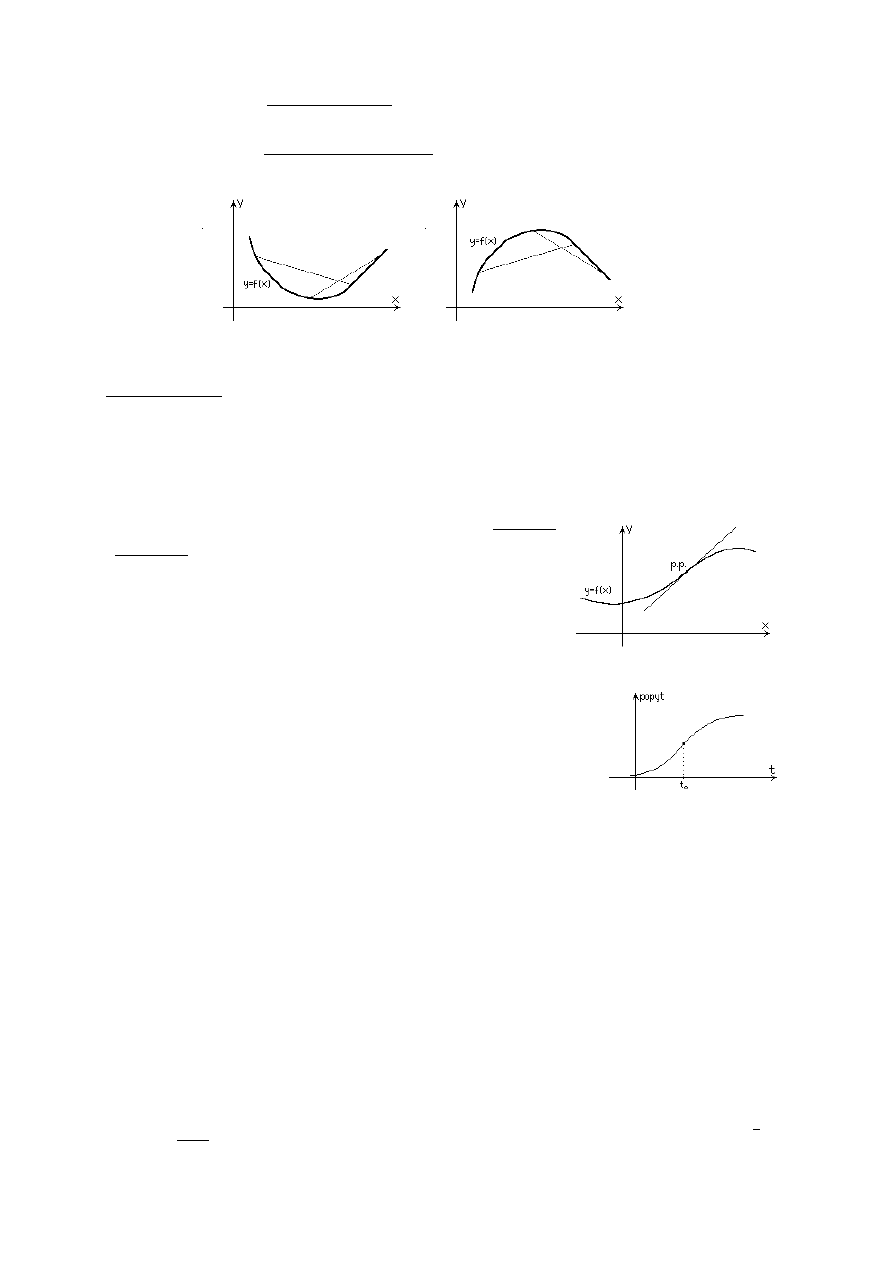
Funkcja
)
(x
f
jest wypukła w górę na przedziale
f
D
I
, jeżeli każdy odcinek łączący dwa
dowolne punkty wykresu tej funkcji leży pod wykresem lub się z nim pokrywa.
Funkcja
)
(x
f
jest ściśle wypukła w górę na przedziale
f
D
I
, jeżeli każdy odcinek łączący
dwa dowolne punkty wykresu tej funkcji leży pod wykresem.
Na rysunkach przedstawiono funkcje wypukłe w dół i w górę (nie są one ściśle wypukłe).
Twierdzenie (8)
Jeżeli dla każdego
)
;
( b
a
x
funkcja
)
(x
f
spełnia nierówność
0
)
(
x
f
, to jest ona ściśle
wypukła w dół.
Jeżeli dla każdego
)
;
( b
a
x
funkcja
)
(x
f
spełnia nierówność
0
)
(
x
f
, to jest ona ściśle
wypukła w górę.
Punkt
))
(
,
(
0
0
x
f
x
wykresu funkcji
)
(x
f
jest punktem
przegięcia funkcji, jeżeli funkcja ma w tym punkcie styczną
i zmienia w nim rodzaj wypukłości.
Jeżeli
))
(
,
(
0
0
x
f
x
jest punktem przegięcia funkcji
)
(x
f
i
istnieje
)
(
0
x
f
, to
0
)
(
0
x
f
.
Przykładowo w ekonomii punkt przegięcia rosnącej funkcji
opisującej popyt na pewien rodzaj towaru określa moment
rozpoczęcia spadkowej tendencji wzrostu.
Postępowanie przy badaniu funkcji.
1. Ustalenie dziedziny funkcji.
2. Określenie niektórych podstawowych własności funkcji: parzystość lub nieparzystość,
okresowość, miejsca zerowe, ciągłość.
3. Obliczenie granic funkcji na końcach dziedziny i wyznaczenie ewentualnych asymptot
funkcji.
4. Wyznaczenie pierwszej pochodnej, ustalenie przedziałów monotoniczności funkcji oraz
ekstremów funkcji.
5. Wyznaczenie drugiej pochodnej , ustalenie przedziałów wypukłości i punktów przegięcia.
6. Sporządzenie tabeli przebiegu zmienności funkcji.
7. Sporządzenie wykresu funkcji.
Zadanie. Przeprowadzić badanie funkcji
a)
2
1
)
(
x
x
x
f
, b)
x
e
x
x
f
)
3
(
)
(
, c)
x
x
x
f
ln
)
(
2
, d)
x
e
x
x
f
3
2
)
(
, d)
x
xe
x
f
1
)
(
.
Wyszukiwarka
Podobne podstrony:
POCHODNA FUNKCJI ZASTOSOWANIE POCHODNYCH
pochodna-funkcji-zastosowania
pochodna funkcji, wyklad id 364 Nieznany
6, 7 zastosowania pochodnej funkcji
Wybrane zastosowania pochodnej funkcji, Analiza matematyczna
Lista 7 - Zastosowania pochodnych funkcji jednej zmiennej, Studia, Matematyka
Pochodne funkcji zlozonych Za Rozwiazanie zadania domowego id
Pochodne funkcji zlozonych Za Zadanie domowe id 810241
Pochodna funkcji – teoria oraz przykładowe zastosowania
Pochodne funkcji 4 id 364442 Nieznany
W 3 Pochodna funkcji i jej zastosowania
Pochodne zadania cz 2 id 364419
pochodne wyzszych rzedow id 364 Nieznany
4 pochodna funkcji jednej zmiennej
więcej podobnych podstron