Narysuj wykres funkcji liniowej podanej wzorem y = 3x-1, a następnie podaj
miejsce zerowe tej funkcji,
argumenty, dla których funkcja przyjmuje wartości dodatnie,
argument, dla którego wartość funkcji wynosi 7,
miejsce przecięcia z osią y,
czy funkcja jest rosnąca czy malejąca.
Wyznaczyć dziedzinę funkcji:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
6)![]()
7) ![]()
8) ![]()
9) ![]()
10) ![]()
Stosując odpowiednie przekształcenia narysuj wykres funkcji f(x), a następnie odczytaj zbiór wartości oraz monotoniczność tej funkcji, jeżeli:
Narysuj funkcje:
Mając wykres funkcji f(x) sporządź wykresy następujących funkcji:
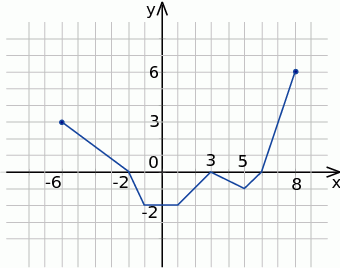
Odczytaj z wykresu funkcji f:dziedzinę i zbiór wartości
argumenty, dla których funkcja przyjmuje wartości nieujemne
argumenty, dla których funkcja przyjmuje wartości większe od 1
przedziały monotoniczności
odczytaj f(0), f(5), f(7)
wartość najmniejszą i największą
narysuj wykres funkcji g(x)=f(x)+2
narysuj wykres funkcji h(x)=f(x-2)
Funkcja liczbowa określona jest następująco:
Oblicz wartość funkcji f odpowiednio dla argumentów 2, -3, 3.
Sprawdź, która z liczb -3, 0, 2, 4 jest miejscem zerowym funkcji f.
Wyznacz te argumenty, dla których funkcja f przyjmuje wartość - 4.
Sporządź wykres funkcji f.
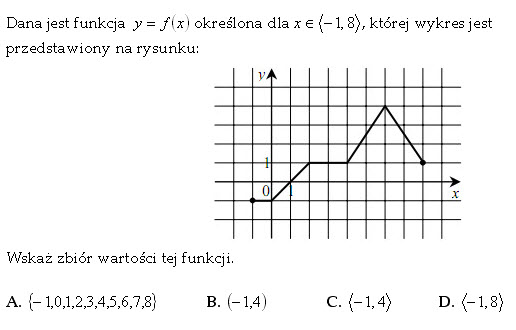
Dana jest funkcja f(x) określona dla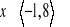
, której wykres przedstawiony jest na rysunku. Wskaż dziedzinę funkcji, zbiór wartości, monotoniczność, wartość najmniejszą i największą oraz przedziały, dla których funkcja przyjmuje wartości dodatnie i ujemne.Podaj wektor, o który została przesunięta funkcja f(x), tworząc funkcję g(x), jeżeli:
f(x)=|x| g(x)=|x+2|-4
f(x)=x2 g(x)=(x-3)2+1
f(x)=2x g(x)=2x+3-2
f(x)=
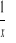
g(x)=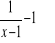
a) |
b) |
c) |
d) |
e) |
f) |
g) |
h) |
i) |
j) |
|
|
a) 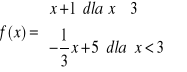
b) 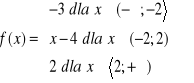
c) 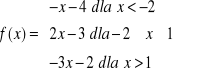
d) 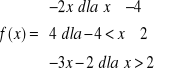
oraz określ monotoniczność, zbiór wartości, wartość najmniejszą i największą (o ile istnieje) oraz miejsca zerowe.
a(x)=-f(x); b(x)=f(-x); c(x)=-f(-x); d(x)=f(x-3)-1; e(x)=2f(x); g(x)=f(2x); h(x)=f(|x|); i(x)=f(-|x|); j(x)=|f(x)|
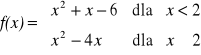
Wyszukiwarka
Podobne podstrony:
funkcja własności, Matematyka, Liceum
funkcja kwadratowa (2), Matematyka, Liceum
funkcja wykładnicza, Matematyka, Liceum
przeksztalcenie funkcji homograficznej, Matematyka, Liceum
miejsca zerowe funkcji kwadratowej, Matematyka, Liceum
funkcja kwadratowa, Matematyka, Liceum
funkcja kwadratowa 2, Matematyka, Liceum
wlasnosci funkcji, Matematyka, Liceum
wlasnosci funkcji, Matematyka, Liceum
Funkcje trygonometryczne, Sprawdziany, Liceum, Matematyka
Funkcja kwadratowa, Matematyka - zadania liceum
przesuwanie wykresu funkcji, Matematyka, Liceum
Zadania dotyczace funkcji liniowej i jej wlasnosci, Matematyka. Zadania i rozwiązania
funkcje trygonometrczne podstawa, Matematyka, Liceum
Funkcje - 30 zadań, Matematyka liceum
Funkcja kwadratowa, Sprawdziany, Liceum, Matematyka
Funkcja kwadratowa i jej wlasnosci, Matematyka. Zadania i rozwiązania
więcej podobnych podstron