Układ równań liniowych, dyskusja ilości rozwiązań.

1. Definicja:

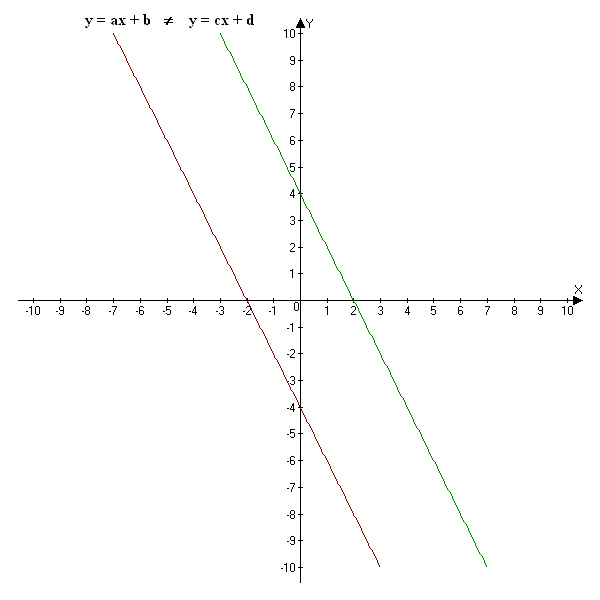
Układ równań liniowych to układ równań, które mają niewiadome co najwyżej stopnia I, np.:

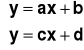
gdzie a, b, c, d - stałe

2. Metoda wyznaczników:

Zabierzmy układ równań postaci:

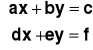
W celu rozwiązania go metodą wyznaczników, obliczamy wyznaczniki układu według wzorów:

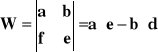
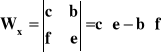
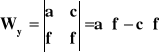
Teraz (przy odpowiednich założeniach, które rozpatrzymy później):

3. Dyskusja ilości parametrów:

1. Jeśli W≠0, to układ jest oznaczony, zatem prawdziwe są wzoru z punktu 2:

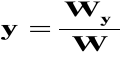
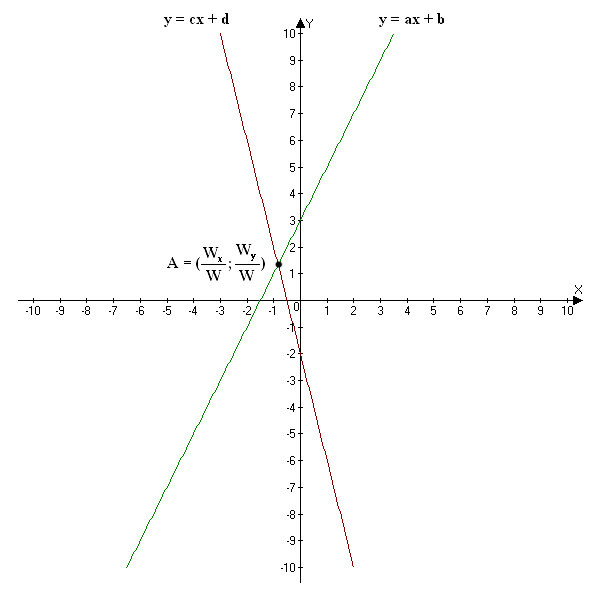
2. Jeśli W=0, a także W_x=0 i W_y=0, to układ jest nieoznaczony - ma nieskończenie wiele rozwiązań:

x, y ∈ R

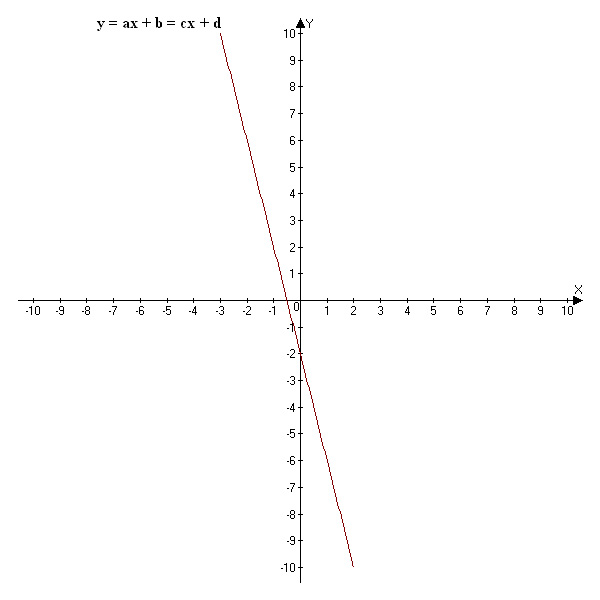
3. Jeśli W = 0 i co najmniej jeden z pozostałych wyznaczników nie jest zerem, to układ jest sprzeczny:

x, y ∈ ∅

Podsumowując:

1. W = 0 ⇒
   ∧
   

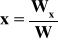
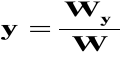
b) W = 0 ∧ W_x = 0 ∧ W_y = 0 ⇒ x, y ∈ R

c) W=0 ∧ (W_x ≠ 0 ∨ W_y ≠ 0) ⇒ x, y ∈ ∅

© Marcin Kordasz, IVa