Interpretacja geometryczna całki oznaczonej.

Jeżeli w przedziale [a,b]
, to pole obszaru ograniczonego łukiem krzywej
odcinkiem osi 0x oraz prostymi
równa się całce oznaczonej

Jeśli zaś w przedziale [a,b] jest
to pole równa się

Obliczanie długości łuku.

Jeśli krzywa jest wyznaczona
przy czym f(x) ma w przedziale [a,b] pochodną ciągłą to długość łuku L wynosi

x=g(t), y=h(t) dla

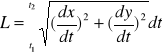
Objętość bryły powstałej przez obrót krzywej y=f(x) (ciągłej i niemniejszej od zera) dla
wokół osi 0x to

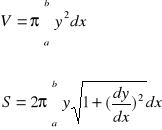
To jest pole powierzchni bocznej dla ww. przypadku przy założeniu ciągłości pierwszej pochodnej.