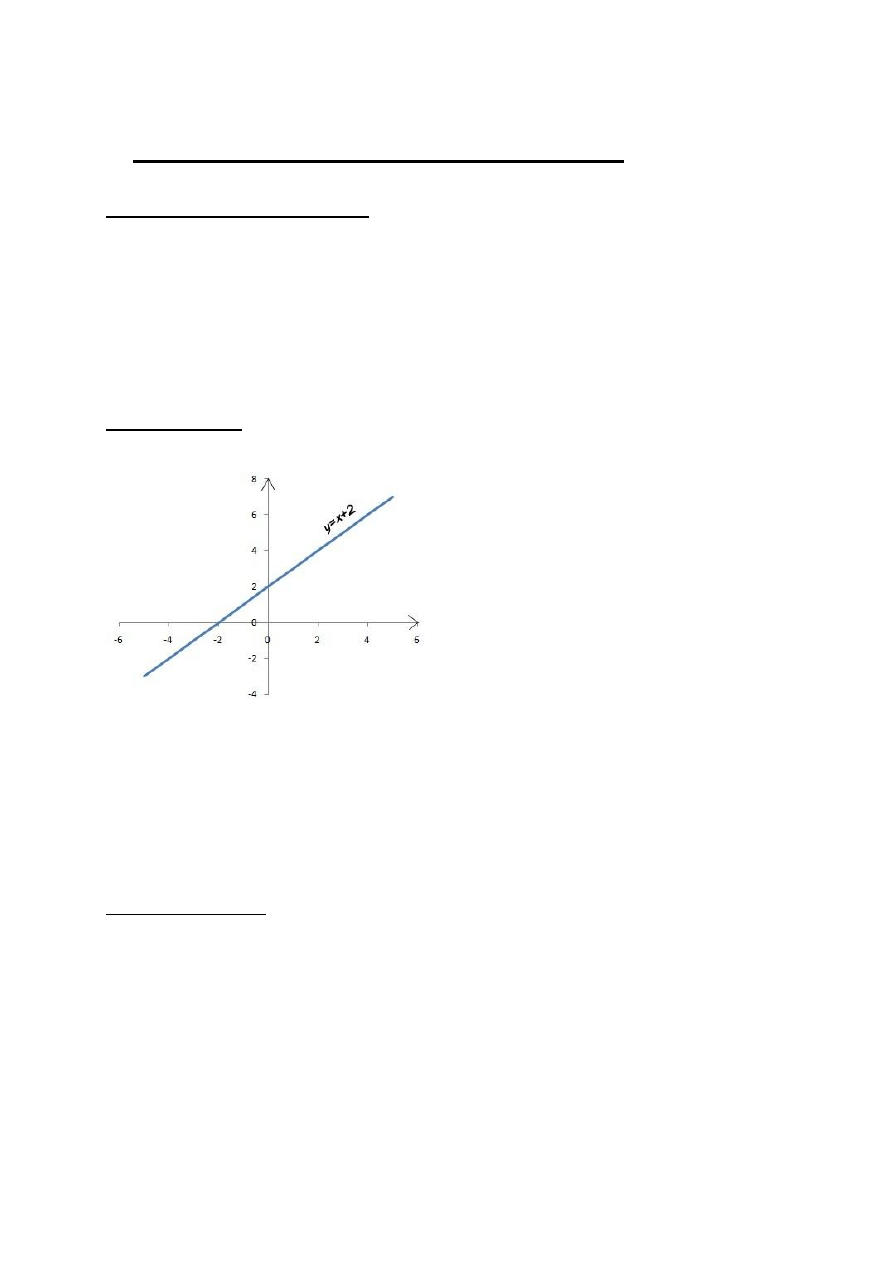
1

Misztal Aleksandra, Herman Monika

7. Funkcje elementarne i ich własności.

Definicja funkcji elementarnej

Podstawowymi funkcjami elementarnymi nazywamy funkcje:
• stałe
• potęgowe, np.

• wykładnicze
• logarytmiczne
• trygonometryczne
Funkcje, które można otrzymać z podstawowych funkcji elementarnych za pomocą skończonej liczby
działań arytmetycznych oraz operacji złożenia funkcji (np. logx) nazywamy funkcjami elementarnymi.

Funkcja liniowa

Funkcję określoną wzorem ( ) nazywamy funkcją liniową.
Litery a i b oznaczają liczby dane, a nazywamy współczynnikiem kierunkowym, b-wyrazem wolnym.



Gdy a=0, to funkcja liniowa jest stała,



Gdy , to funkcja liniowa jest monotoniczna, dla a>0 rosnąca, a dla a<0 malejąca.



Jest ciągła i różnowartościowa.



Jeśli funkcje liniowe mają ten sam współczynnik kierunkowy a, to ich wykresy są prostymi
równoległymi.



Jeśli dwie funkcje liniowe mają współczynniki kierunkowe, których iloczyn jest równy -1, to
ich wykresy są prostymi prostopadłymi.



Współczynnik a odpowiada za kierunek, zaś współczynnik b za miejsce przecięcia z osią.

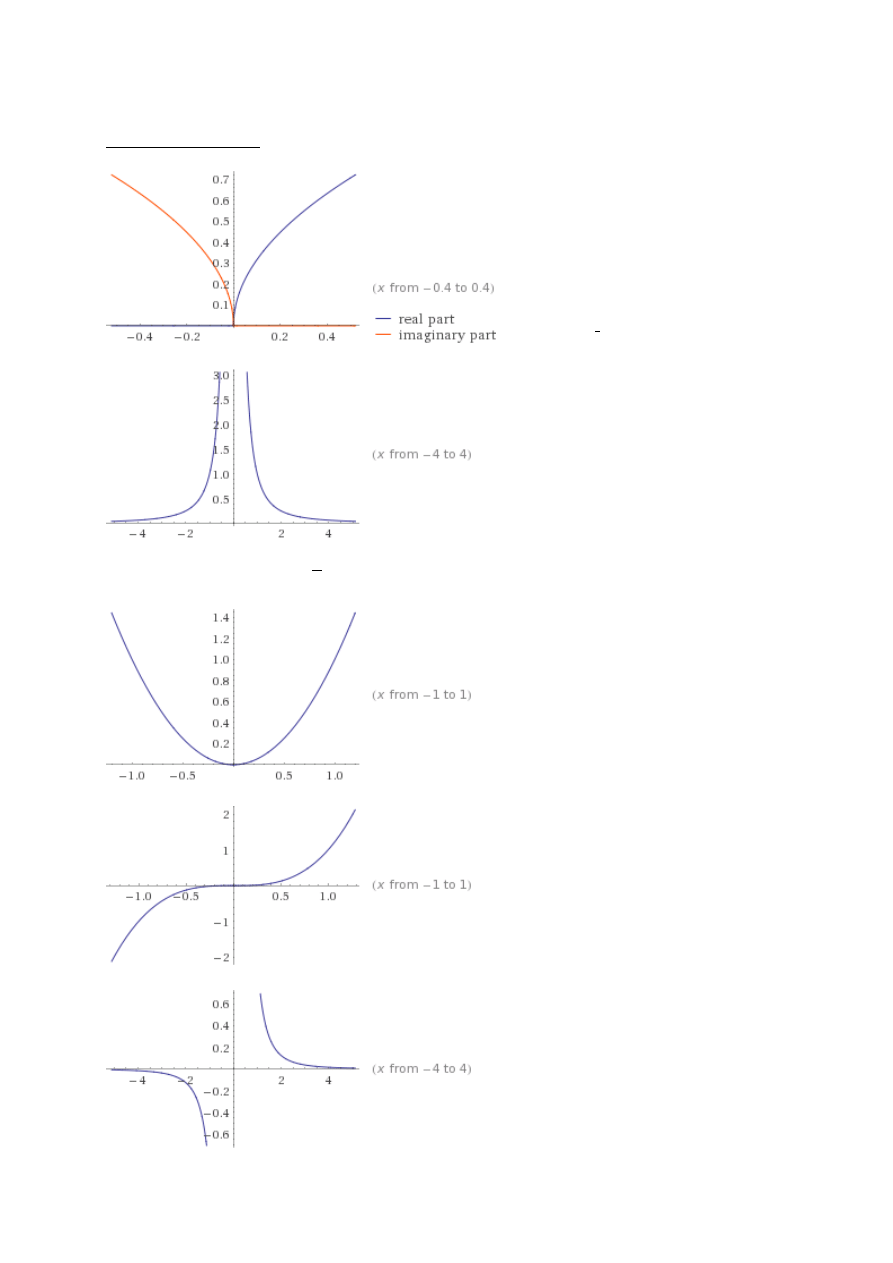
Funkcją potęgową

nazywamy funkcją postaci ( )

.



Dziedzina tej funkcji zależy od wartości a.



Jeżeli a jest liczbą całkowitą dodatnią, to dziedzina tej funkcji jest całym zbiorem liczb
rzeczywistych.



W przypadku gdy, a jest liczbą całkowitą niedodatnią to dziedziną tej funkcji jest { }.



Jeżeli wykładnik a>0, to funkcja jest rosnaca w przedziale ), a jeśli a<0,
to jest malejąca w tym przedziale.

2

Wykres - przykłady

( )

( )

Funkcje ( )

( ) √ są wzajemnie odwrotne.

( )

( )

( )

3

( )

( )

WŁASNOŚCI FUNKCJI POTĘGOWEJ

Dla a,b>0 oraz mamy:

(

)

( )

(

)

.

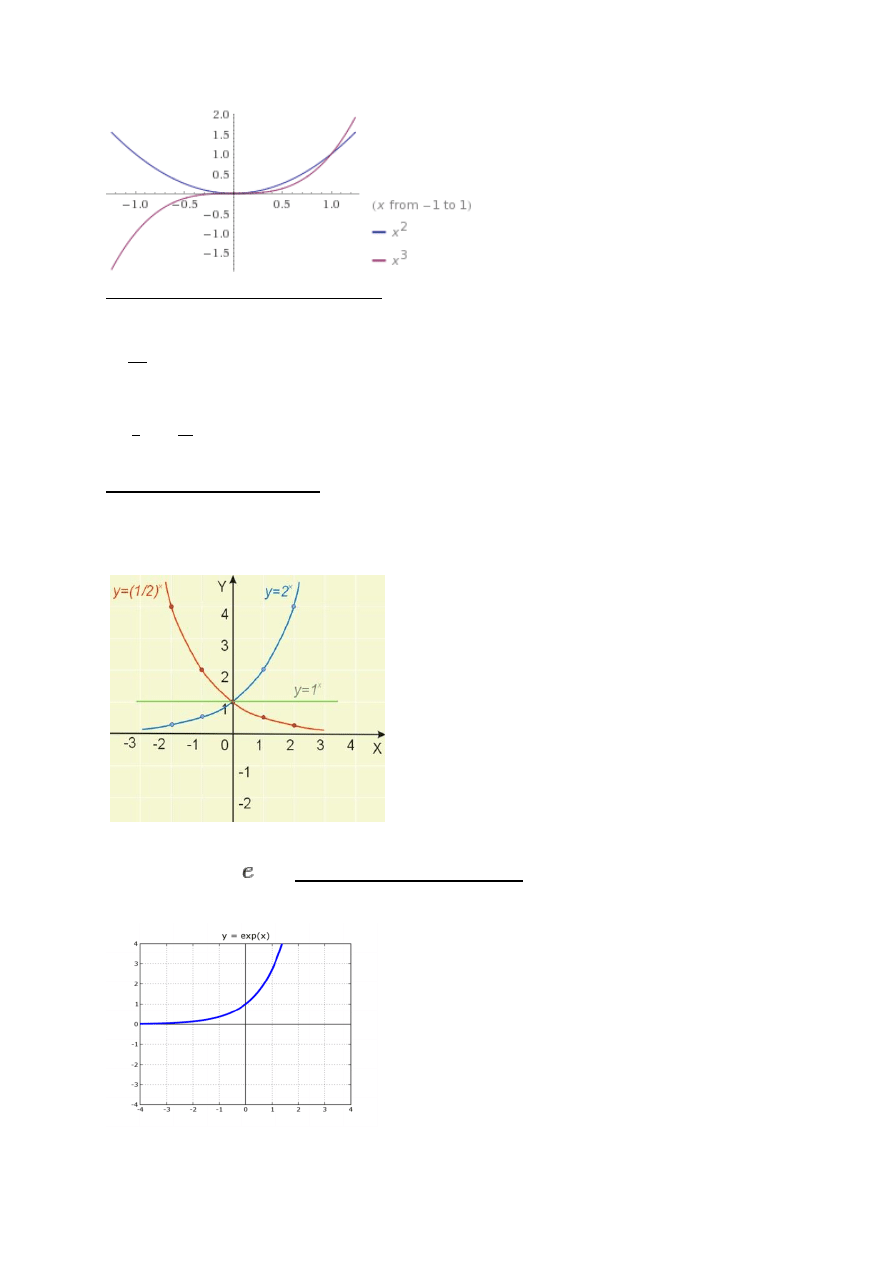
FUNKCJA WYKLADNICZA

nazywamy funkcję opisaną wzorem: ( )

,

przy czym liczba ( ) ( ) jest nazywana podstawą funkcji wykładniczej.
Dziedziną funkcji wykładniczej jest , a zbiorem wartości przedział ( )
Gdy ( ), to funkcja jest malejąca, zaś gdy ( ), to funkcja jest rosnąca.

Szczególnym przykładem funkcji wykładniczej, jest funkcja eksponencjalna, czyli funkcja wykładnicza
o podstawie równej (czyli podstawie logarytmu naturalnego).
Wzór funkcji: ( )

4

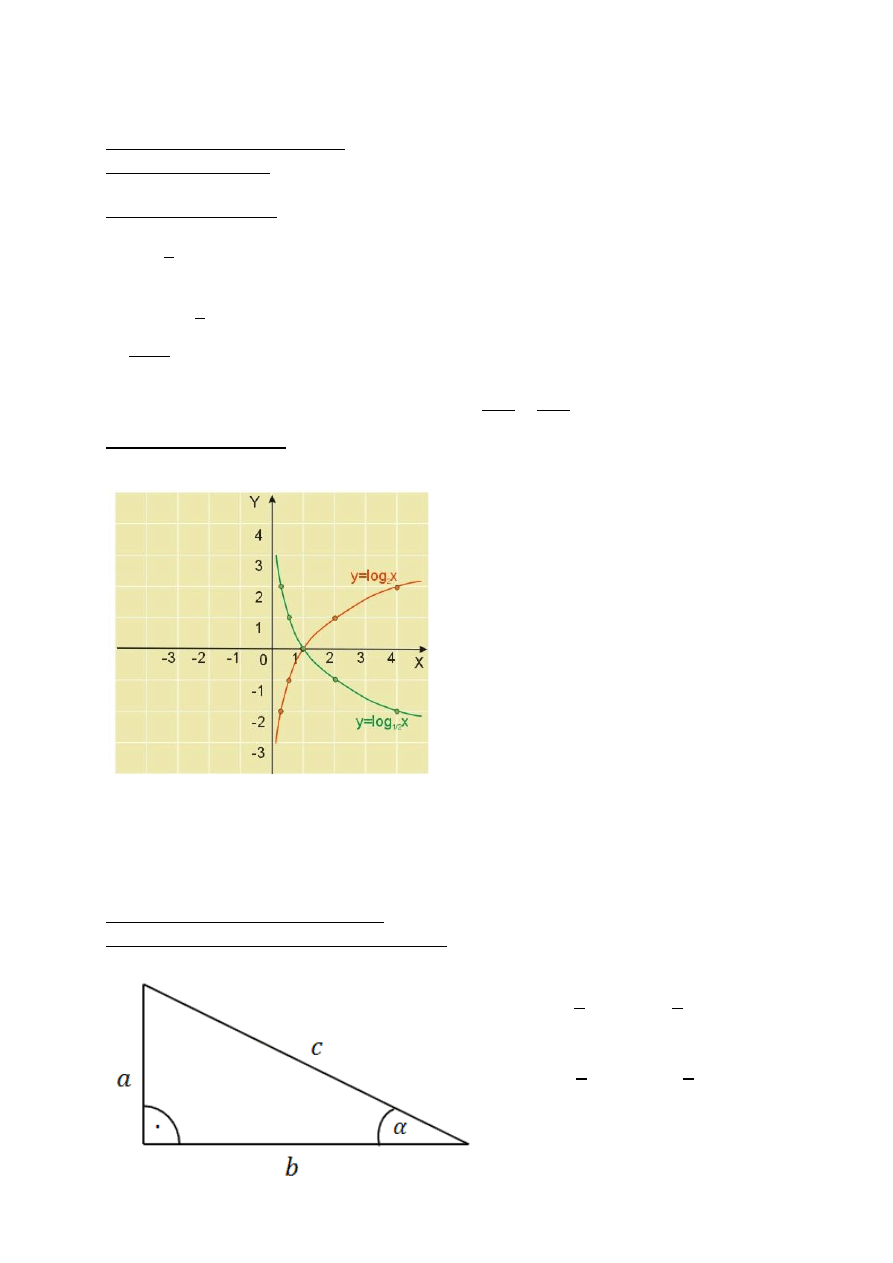
FUNKCJA LOGARYTMICZNA

Definicja logarytmu:

Dla oraz x>0 logarytmem przy podstawie a z liczby x nazywamy

taką liczbę że

i piszemy

Wzory logarytmiczne

: Dla oraz x,y>0 zachodzą następujące równości:

( )

(

)



Jak się mają do siebie:

Funkcją logarytmiczną

przy podstawie a, gdzie ( ) ( ),

nazywamy funkcję określoną wzorem: ( )

.



Dziedziną funkcji logarytmicznej jest

.



Wartościami jest cały zbiór liczb rzeczywistych.



Funkcja jest różnowartościowa.



Jeżeli ( ) to funkcja jest malejąca, a gdy ( ) jest rosnąca.



Funkcją odwrotną do funkcji logarytmicznej jest funkcja wykładnicza ( )

.

FUNKCJE TRYGONOMETRYCZNE

Funkcje trygonometryczne kąta ostrego α

wyrażają stosunki długości odpowiednich boków

w trójkącie prostokątnym mającym kąt α.

5

Wykresy funkcji trygonometrycznych

Definicja funkcji sinus i cosinus
Dla kładziemy:

( ) ∑

( )

( )

( ) ∑

( )

( )

I nazywamy odpowiednio sinusem x oraz cosinusem x. Funkcje
nazywamy odpowiednio funkcją sinus i funkcją cosinus i odpowiednio oznaczamy sin i cos.
Przy czym szeregi (*) i (**) są zbieżne bezwzględnie dla każdego .

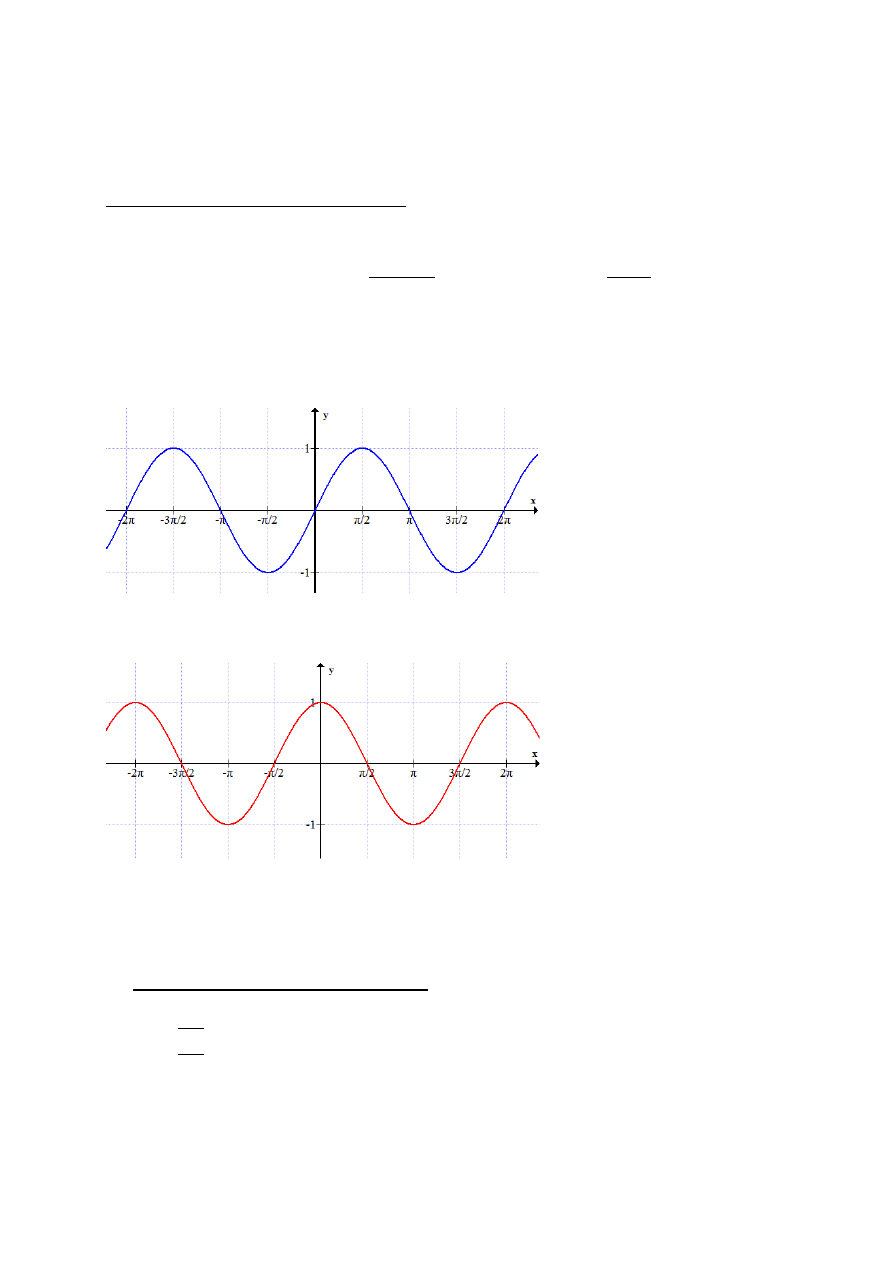
f(x)=sinx



Dziedziną funkcji jest



Zbiór wartości [-1,1]



Okres wynosi 2

f(x)=cosx



Dziedziną funkcji jest



Zbiór wartości [-1,1]



Okres wynosi 2

Definicja funkcji tangens i cotangens

Niech

Liczbę

gdy nazywamy tangensem i oznaczamy tg

Liczbę

gdy nazywamy cotangensem i oznaczamy ctg.

Funkcję określoną w zbiorze { } nazywamy funkcją tangens i
oznaczamy tg.
Funkcję określoną w zbiorze { } nazywamy funkcją cotangens i
oznaczamy ctg.

6

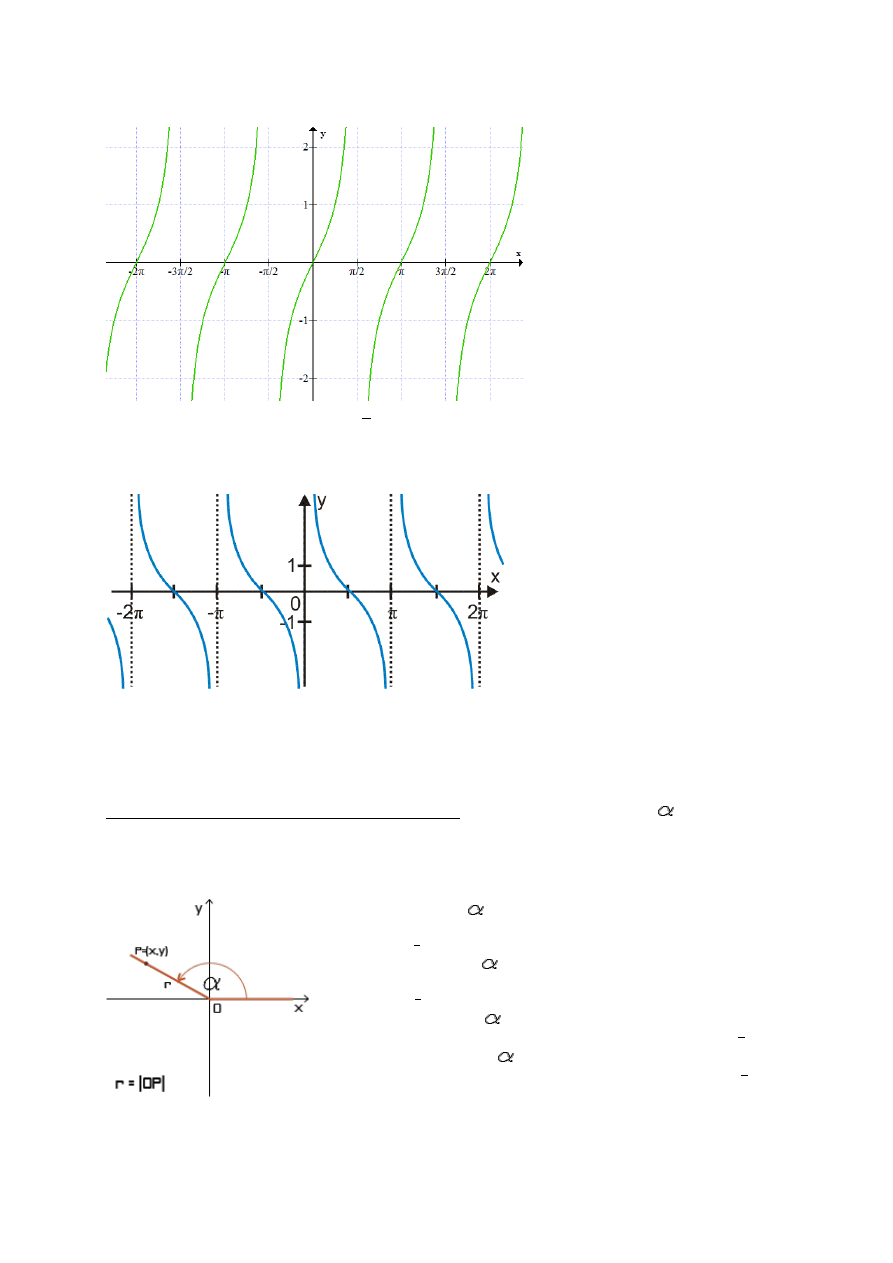
f(x)=tgx



Dziedziną jest bez punktów

+k , k jest dow liczbą całkowitą.



Zbiorem wartości jest



Okres wynosi



Jest funkcją rosnącą

f(x)=ctgx



Dziedziną jest bez punktów k , k jest dow liczbą całkowitą.



Zbiorem wartości jest



Okres wynosi



Jest funkcją malejącą

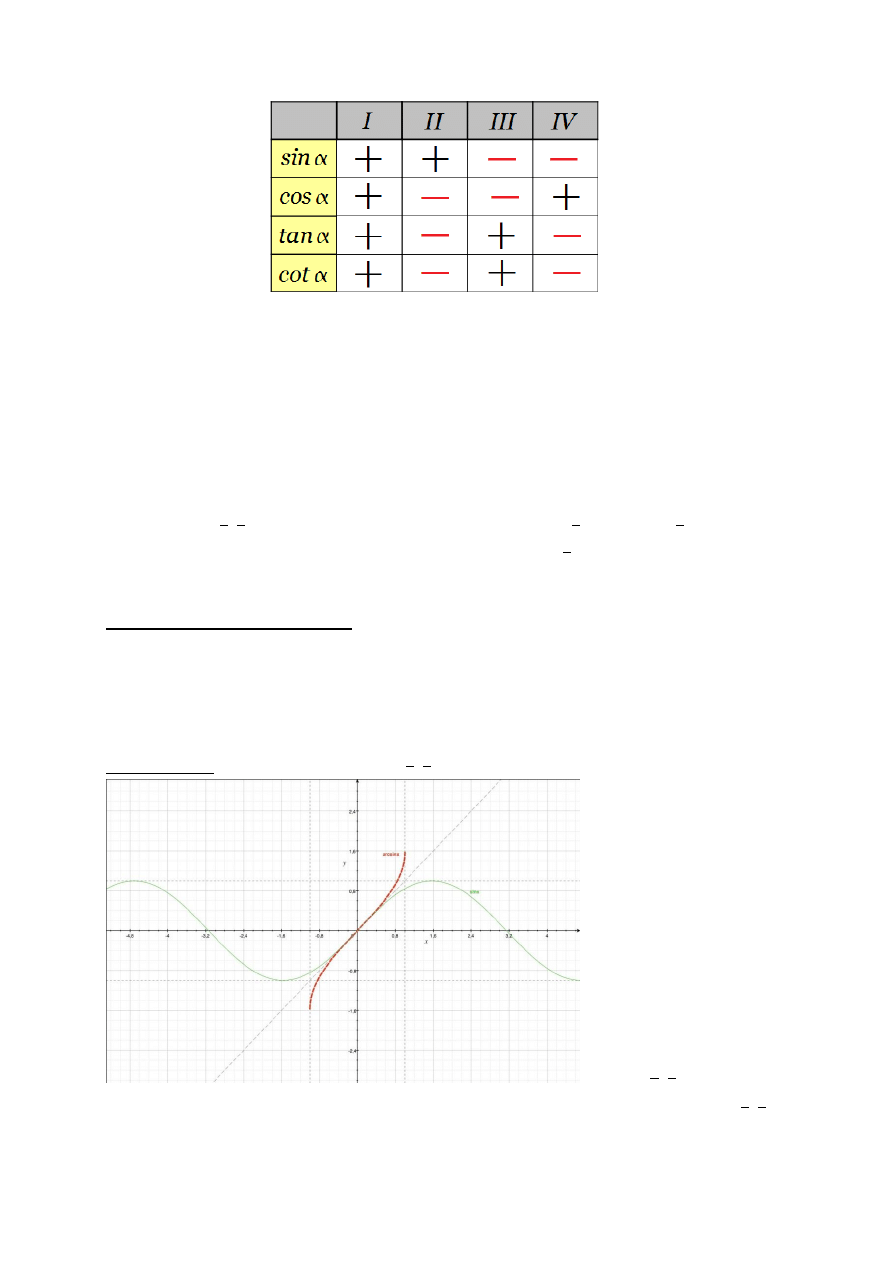
Funkcje trygonometryczne dowolnego kata

- Jeżeli dany kąt skierowany

ustawimy w

układzie współrzędnych tak aby wierzchołek kąta był początkiem układu a oś x (odcięta) była
ramieniem początkowym kąta i punkt P leżał na ramieniu końcowym kąta to możemy wyróżnić
następujące funkcje tego kąta.

Sinusem dowolnego kąta

nazywamy stosunek rzędnej dowolnego punktu

leżącego na końcowym ramieniu tego kąta do długości promienia wodzącego tego
punktu.

Cosinusem dowolnego kąta

nazywamy stosunek odciętej dowolnego punktu

leżącego na końcowym ramieniu tego kąta do długości promienia wodzącego tego
punktu.

Tangensem dowolnego kąta

nazywamy stosunek rzędnej dowolnego punktu

leżącego na końcowym ramieniu tego kąta do odciętej tego punktu.

Cotangensem dowolnego kąta

nazywamy stosunek odciętej dowolnego punktu

leżącego na końcowym ramieniu tego kąta do rzędnej tego punktu.

7

Funkcje sin i cos określone są dla wszystkich kątów . Tg nie jest określony dla kątów
, gdzie k jest dowolną liczbą całkowitą. Ctg nie jest określony dla kątów , gdzie k
jest dowolną liczbą całkowitą.
Wszystkie funkcje trygonometryczne są okresowe.

PRZYKŁADY
Rozwiązać równanie:

Równanie to jest równoważne alternatywie równań:

W przedziale (

) pierwsze z tych równań ma rozwiązanie

a drugie

.

Zatem rozwiązaniem wyjściowego równania jest każda liczba

.

FUNKCJE CYKLOMETRYCZNE

Funkcja cyklometryczna jest funkcją odwrotną do funkcji trygonometrycznej. Otrzymujemy ją po
zawężeniu funkcji trygonometrycznej do maksymalnego przedzialu, w którym ta funkcja jest
różnowartościowa. Wszystkie wykresy funkcji cyklometrycznych uzyskujemy zgodnie z zasadą
sporządzania wykresów funkcji odwrotnych, stosując symetrię względem prostej y=x.

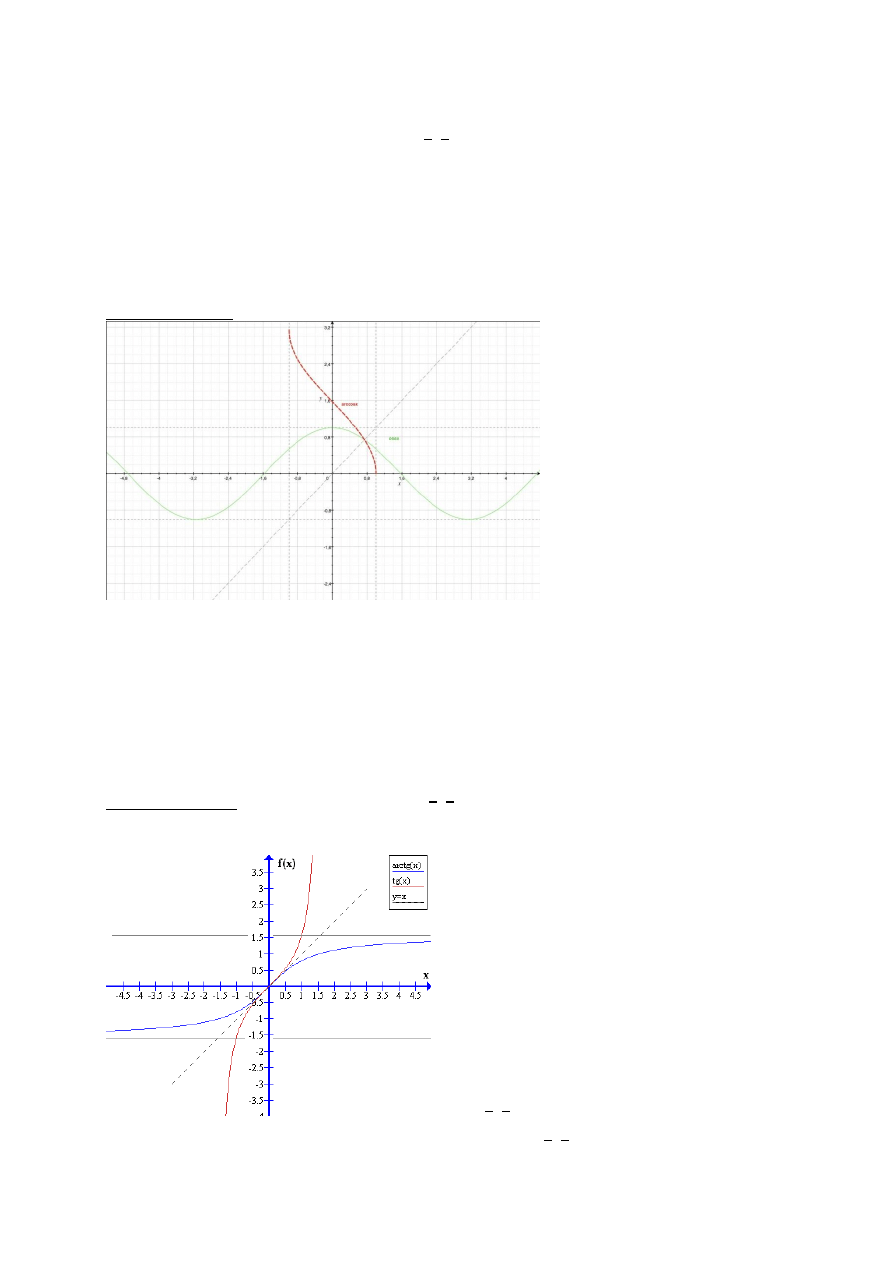
Funkcję sinus

zawężamy do przedziału 〈

〉, funkcję odwrotną do niej oznaczamy f(x) = arcsinx.

[

] ]

] [

]

8

Jej dziedziną jest <-1,1>, a zbiorem wartości 〈

〉.

Jest to funkcja:



Rosnąca



Nieparzysta



Odwracalna



Ciągła



Ograniczona

Funkcję cosinus

zawężamy do przedziału 〈 〉, funkcję odwrotną do niej oznaczamy f(x)=arccosx

] ]

arccosx: ] ]

Jej dziedziną jest <-1,1>, a zbiorem wartości 〈 〉.
Jest to funkcja:



malejąca



Odwracalna



Ciągła



Ograniczona

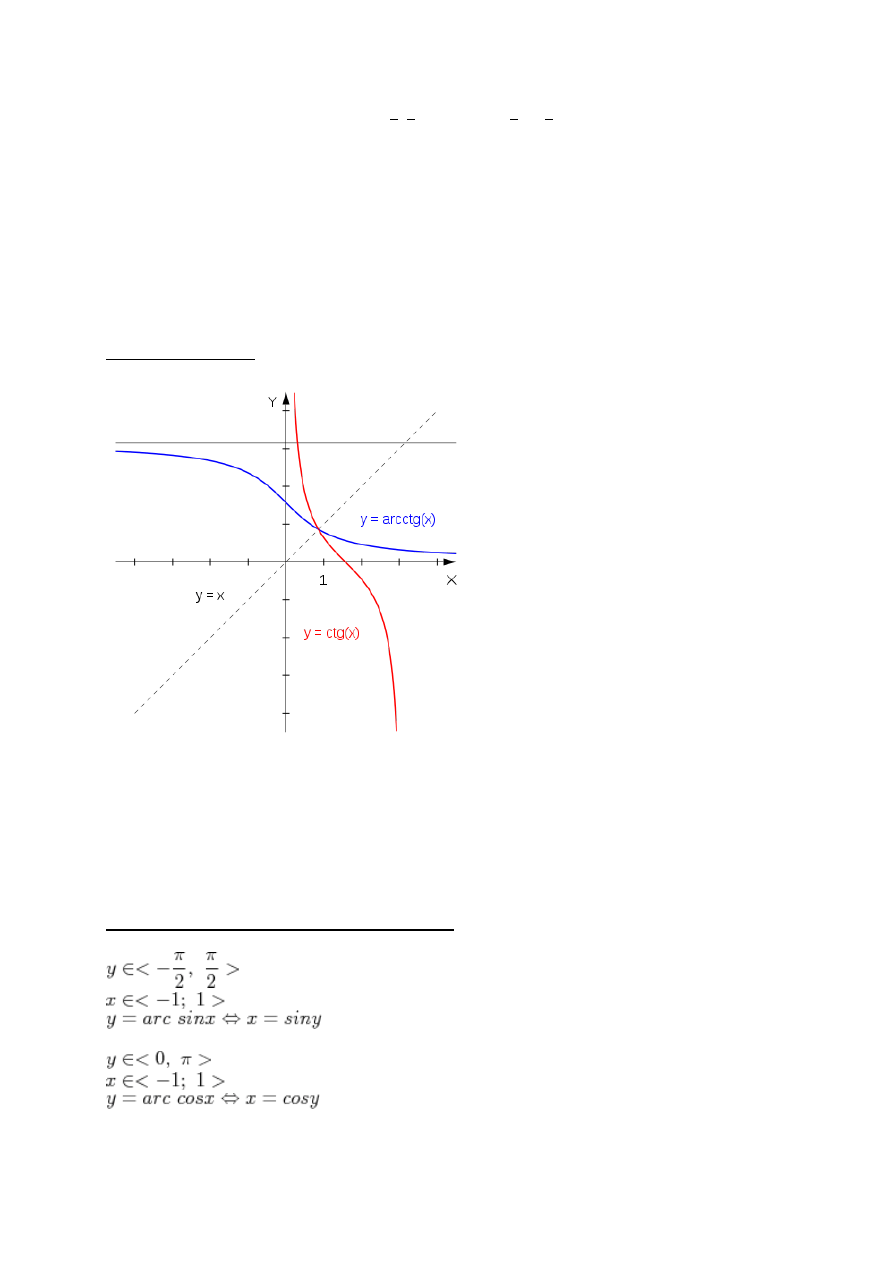
Funkcję tangens

zawężamy do przedziału 〈

〉, funkcję odwrotną do niej oznaczamy

f(x)=arctgx

(

)

(

)

9

Jej dziedziną jest a zbiorem wartości 〈

〉, proste y=

i y=

są asymptotami poziomymi

wykresu.

Jest to funkcja:



Rosnąca



nieparzysta



Odwracalna



Ciągła



Ograniczona

Funkcję cotangens

zawężamy do przedziału ( ), funkcję odwrotną do niej oznaczamy

f(x)=arcctgx.

( )

( )

Jej dziedziną jest a zbiorem wartości 〈 〉, proste y=0 i y=π są asymptotami poziomymi wykresu.
Jest to funkcja:



malejąca



Odwracalna



Ciągła



Ograniczona



OBLICZENIA FUNKCJI CYKLOMETRYCZNYCH