Otoczenie i Sąsiedztwo
Niech x 0 ∈ R oraz δ > 0 .
• Przedział ( x 0 − δ , x 0 + δ ) nazywamy otoczeniem punktu x 0
o promieniu δ i oznaczamy U ( x 0 , δ) .
• Przedział h x 0 , x 0 + δ ) nazywamy otoczeniem prawostronnym
punktu x 0 o promieniu δ .
• Przedział
( x 0 − δ , x 0 i nazywamy otoczeniem lewostronnym
punktu x 0 o promieniu δ .
Zauważmy, że
x ∈ U ( x 0 , δ) ⇐⇒ | x − x 0 | < δ
• Przedział ( x 0 , x 0 + δ ) nazywamy sąsiedztwem prawostronnym
punktu x 0 o promieniu δ .
• Przedział ( x 0 − δ , x 0 ) nazywamy sąsiedztwem lewostronnym
punktu x 0 o promieniu δ .
• Sumę tych dwóch przedziałów nazywamy sąsiedztwem punktu x 0
o promieniu δ i oznaczamy S( x 0 , δ) , tj.
S( x 0 , δ) = ( x 0 − δ , x 0 ) ∪ ( x 0 , x 0 + δ ) = ( x 0 − δ , x 0 + δ )r { x 0 }
Zauważmy, że
x ∈ S( x 0 , δ) ⇐⇒ 0 < | x − x 0 | < δ
• Przedział ( δ , + ∞ ) nazywamy otoczeniem plus nieskończoności.
• Przedział ( −∞ , δ ) nazywamy otoczeniem minus nieskończoności.
• W tym przypadku otoczenie i sąsiedztwo są tymi samymi zbiorami.
Granica funkcji
f : D → R ,
D ⊂ R
x 0 ∈ D
lub
∃{xn}∈D xn −→ x 0
Definicja
Niech f będzie określona przynajmniej w sąsiedztwie punktu x 0 . Funkcja f ma w punkcie x 0 granicę g , co zapisujemy lim f ( x) = g,
x→x 0
gdy dla dowolnego otoczenia U punktu g istnieje sąsiedztwo S
punktu x 0 takie, że dla każdego x ∈ S wartość f ( x) należy do otoczenia U .
5
• Jeżeli x 0 ∈ R i g ∈ R , to mamy: lim f ( x) = g
⇐⇒
x→x 0
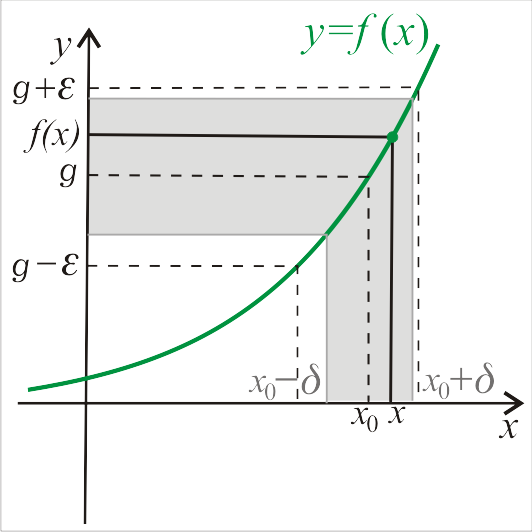
∀ε> 0 ∃δ> 0 ∀x∈D
0 < | x − x 0 | < δ
⇒
| f ( x) − g | < ε
( Definicja Cauchy’ego granicy właściwej w punkcie )
• Jeżeli x 0 = + ∞ i g ∈ R , to mamy: lim
f ( x) = g
⇐⇒
x→+ ∞
∀ε> 0 ∃K> 0 ∀x∈D
x > K
⇒
| f ( x) − g | < ε
( Definicja Cauchy’ego granicy właściwej w plus nieskończoności )
• Napisz definicję Cauchy’ego granicy właściwej w minus nieskończoności.
• Jeżeli x 0 ∈ R i g = −∞ , to mamy: lim f ( x) = −∞
⇐⇒
x→x 0
∀M< 0 ∃δ> 0 ∀x∈D
0 < | x − x 0 | < δ
⇒
f ( x) < M
( Definicja Cauchy’ego granicy niewłaściwej (= −∞) w punkcie )
• Napisz definicję Cauchy’ego granicy niewłaściwej (= + ∞) w punkcie.
• Jeżeli x 0 = + ∞ i g = + ∞ , to mamy: lim
f ( x) = + ∞
⇐⇒
x→+ ∞
∀M> 0 ∃K> 0 ∀x∈D
x > K
⇒
f ( x) > M
( Definicja Cauchy’ego granicy niewłaściwej (= + ∞) w plus nieskończoności )
• Napisz definicję Cauchy’ego granicy niewłaściwej (= + ∞) w minus nieskończoności.
• Napisz definicję Cauchy’ego granicy niewłaściwej (= −∞) w plus nieskończoności.
• Napisz definicję Cauchy’ego granicy niewłaściwej (= −∞) w minus nieskończoności.
Przykład
Wykaż, korzystając z definicji Cauchy’ego granicy
funkcji, że
lim ( 2 x − 7 ) = − 5 .
x→ 1
Definicja Heinego granicy
Definicja
g ( g ∈ R lub g = ±∞ ) jest granicą funkcji f w
x 0 ( x 0 ∈ R lub x 0 = ±∞ ) wtedy i tylko wtedy, gdy dla dowolnego ciągu { xn } , takiego, że xn ∈ S( x 0) ⊂ D , zachodzi lim
x
f ( x
n→∞
n = x 0
= ⇒
lim
n→∞
n) = g.
Przykład
Wykaż, korzystając z definicji Heinego granicy funkcji,
że
3 x + 1
1
lim
=
.
x→ 2 5 x + 4
2
Twierdzenie
Definicje: Cauchy’ego i Heinego granicy funkcji są
równoważne.
(
)
(
)
Fakt
Jeżeli istnieją ciągi
x0n i x00n spełniające warunki:
•
lim
x0
n→∞
n = x 0 , przy czym x0n 6= x 0 dla n ∈ N oraz lim
f ( x0
n→∞
n) = g0,
•
lim
x00
n→∞
n = x 0 , przy czym x00
n 6= x 0 dla n ∈ N oraz
lim
f ( x00
n→∞
n) = g00,
• g0 6= g00 ,
to granica
lim f ( x) nie istnieje.
x→x 0
Przykład
Wykaż, że granica funkcji
f ( x) = cos x
w plus
nieskończoności nie istnieje.
Wnioski z definicji Heinego granicy
Twierdzenie
(Arytmetyka granic funkcji)
Jeżeli funkcje f i g
mają granice właściwe w x 0 , to
•
lim ( f ( x) ± g( x) ) =
lim f ( x) ±
lim g( x) ,
x→x 0
x→x 0
x→x 0
•
lim ( c · f ( x) ) = c ·
lim f ( x) ,
gdzie c ∈
x→x
R ,
0
x→x 0
•
lim ( f ( x) · g( x) ) =
lim f ( x) ·
lim g( x) ,
x→x 0
x→x 0
x→x 0
lim
f ( x)
f ( x)
x→x
•
lim
=
0
,
o ile
lim g( x) 6= 0 .
x→x 0 g( x)
lim
g( x)
x→x
x→x
0
0
Twierdzenie
lim f ( x) = 0
⇐⇒
lim | f ( x) | = 0
x→x 0
x→x 0
Twierdzenie
Załóżmy, że funkcje
f
i
g
są określone w
sąsiedztwie
x 0 . Jeżeli granica funkcji f w x 0 jest równa 0 , a funkcja g jest ograniczona, to
lim f ( x) · g( x) = 0 .
x→x 0
Twierdzenie
Załóżmy, że funkcja f jest określona w sąsiedztwie x 0 . Wówczas
1
f ( x)
lim f ( x) = + ∞ ( −∞)
= ⇒
lim
1 +
= 0 .
x→x
0
x→x 0
f ( x)
Twierdzenie
(O trzech funkcjach)
Jeżeli funkcje f, g i h , określone co najmniej w sąsiedztwie S( x 0) punktu x 0 , spęłniają warunki:
• f ( x) 6 g( x) 6 h( x) dla każdego x ∈ S( x 0)
•
lim f ( x) =
lim h( x) = p ,
x→x 0
x→x 0
to
lim g( x) = p .
x→x 0
Przykład
Korzystając z powyższych twierdzeń wykaż, że
lim sin x = 1 .
x→ 0
x
Fakt
sin x
tg x
lim
= 1
lim
= 1
x→ 0
x
x→ 0
x
Przykład
Oblicz granice:
√
a)
lim x 2 − 2 x+1
b)
lim
3 x 4 − 1
√
+
x 2 + 1 − x
x→ 1
x 2 − 1
x→∞
x 8+3 x+4
c)
lim
x
√
d)
lim
1
−
6
x→−∞
x 2+1
x→ 3
x− 3
x 2 − 9
√
3
e)
lim
sin x
x 4
x
+
x
− tg
x→−∞
x 2
f )
lim
x→ 0 sin 3 x
cos πx
2 x
√
√
−x 3
g)
lim
3 x 3+2
1+sin x− 1 − sin x
h)
lim
x→−∞
3 x 3 − 6
x→ 0
tg x
i)
lim
arcctg x
j)
lim arcsin x+arctg x
x→−∞
x
x→ 0
sin x
Granice jednostronne funkcji
Definicja
Załóżmy, że funkcja
f
jest określona w pewnym
prawostronnym (lewostronnym) sąsiedztwie punktu x 0 ∈ R . Funkcja f
ma w punkcie
x 0 granicę prawostronną (lewostronną) g , co zapisujemy
lim
f ( x) = g
(
lim
f ( x) = g ) ,
x→x+
0
x→x−
0
gdy dla dowolnego otoczenia
U
punktu
g
istnieje sąsiedztwo
prawostronne (lewostronne)
S+ ( S− ) punktu x 0 takie, że dla każdego
x ∈ S+ ( x ∈ S− ) wartość f ( x) należy do otoczenia U .
• Definicja Cauchy’ego granic jednostronnych
lim
f ( x) = g
⇐⇒
x→x+
0
∀ε> 0 ∃δ> 0 ∀x∈D
x 0 < x < x 0 + δ
⇒
| f ( x) − g | < ε
lim
f ( x) = g
⇐⇒
x→x−
0
∀ε> 0 ∃δ> 0 ∀x∈D
x 0 − δ < x < x 0 ⇒ | f ( x) − g | < ε
• Definicja Heinego granic jednostronnych
lim
f ( x) = g
⇐⇒
x→x+
0
∀{x
lim
x
f ( x
n}, xn>x
n = x
n) = g
0
n→∞
0
⇒
lim
n→∞
lim
f ( x) = g
⇐⇒
x→x−
0
∀{x
lim
x
f ( x
n}, xn<x
n = x
n) = g
0
n→∞
0
⇒
lim
n→∞
Ćwiczenie
Napisz definicje granic jednostronnych w przypadku,
gdy g = + ∞ lub g = −∞ .
Twierdzenie
(Warunek dostateczny istnienia granicy)
Dla istnienia granicy
g funkcji f w punkcie x 0 ∈ R potrzeba i wystarcza, by istniały obie granice jednostronne w punkcie x 0 i żeby były sobie równe. Ponadto wówczas
lim f ( x) =
lim
f ( x) =
lim
f ( x) .
x→x 0
x→x+
0
x→x−
0
Uwaga
Twierdzenia sformułowane dla granic funkcji są również
prawdziwe dla granic jednostronnych.
Przykład
Oblicz granice jednostronne:
a)
lim
x 2 − 2 x+1
b)
lim
x 2 − 2 x+1
x→ 2+
x 2 − 4
x→ 2 −
x 2 − 4
c)
lim
8
d)
lim
8
3
s
3
s
x→ 0+
8+8 − 1 x
x→ 0 −
8+8 − 1 x
e)
lim
arccos
tg x
tg x
f )
lim
arccos
x→ 0+
|x|
x→ 0 −
|x|
Ciągłość funkcji
f : D → R ,
D ⊂ R
x 0 ∈ D
Definicja
(Ciągłości funkcji w punkcie)
Niech
f
będzie
określona przynajmniej w otoczeniu punktu x 0 ∈ R . Funkcja f jest ciągła w punkcie x 0 wtedy i tylko wtedy, gdy lim f ( x) = f ( x
x→x
0) .
0
Definicja
Mówimy, że funkcja f jest ciągła w swojej dziedzinie, jeżeli f jest ciągła dla każdego punktu x 0 ∈ D .
Definicja
(Ciągłości jednostronnej funkcji w punkcie)
• Niech f będzie określona przynajmniej w otoczeniu prawostronnym punktu x 0 ∈ R . Funkcja f jest prawostronnie ciągła w punkcie x 0 wtedy i tylko wtedy, gdy
lim
f ( x) = f ( x 0) .
x→x+
0
• Niech f będzie określona przynajmniej w otoczeniu lewostronnym punktu x 0 ∈ R . Funkcja f jest lewostronnie ciągła w punkcie x 0 wtedy i tylko wtedy, gdy
lim
f ( x) = f ( x 0) .
x→x−
0
Twierdzenie
Funkcja jest ciągła w punkcie wtedy i tylko wtedy, gdy
jest w tym punkcie ciągła lewostronnie i prawostronnie.
Własności funkcji ciągłych
Twierdzenie
Jeżeli dwie funkcje f i g określone w tym samym zbiorze D są ciągłe w punkcie x 0 ∈ D , to w punkcie x 0 ciągłe są f
funkcje f + g , f − g , f · g oraz g (ta ostatnia przy założeniu g( x 0) 6= 0 ).
Twierdzenie
Złożenie funkcji ciągłych jest funkcją ciągłą.
Uwaga Mówimy, że funkcja f określona na przedziale domkniętym
[ a, b] jest ciągła, jeżeli:
• f jest ciągła dla każdego x ∈ ( a, b)
• f jest prawostronnie ciągła dla x = a
• f jest lewostronnie ciągła dla x = b .
Twierdzenie Założmy, że funkcja f określona w pewnym przedziale (otwartym lub domkniętym) jest ciągła i odwracalna. Wówczas funkcja odwrotna do funkcji f jest funkcją ciągłą.
Wniosek
Funkcje cyklometryczne są funkcjami ciągłymi.
Uwaga
Wszystkie funkcje elementarne są funkcjami ciągłymi (w
swoich dziedzinach).
Uwaga
(Wykorzystanie ciągłości do obliczania granic)
Założmy, że określona jest funkcja złożona f ( g( x)) oraz, że funkcja f jest ciągła w punkcie
lim g( x) . Wówczas
x→x 0
lim f ( g( x)) = f ( lim g( x)) .
x→x 0
x→x 0
Przykład
Oblicz granice jednostronne e) i f ) z poprzedniego
przykładu.
Przykład
Wiedząc, że
lim f ( x)
=
a > 0
oraz
x→x 0
lim g( x) = b oblicz granicę:
x→x 0
lim f ( x) g( x) .
x→x 0
Przykład
Zbadaj ciągłość funkcji:
x − arccos 0
x 6 0
arctg ln x
0 < x 6 e
f ( x) = 2
e < x 6 4
1
( x− 4)2
x > 4
Rodzaje punktów nieciągłości
• Funkcja f
ma w punkcie
x 0 nieciągłość pierwszego rodzaju,
jeżeli itnieją granicę jednostronne f w tym punkcie, ale lim
f ( x) 6=
lim
f ( x)
x→x+
0
x→x−
0
nieciągłość I rodzaju nieusuwalna (”skok”)
albo
lim
f ( x) =
lim
f ( x)
i
lim f ( x) 6= f ( x 0)
x→x+
x→x 0
0
x→x−
0
nieciągłość I rodzaju usuwalna (”luka”)
.
• Funkcja
f
ma w punkcie
x 0 nieciągłość drugiego rodzaju,
jeżeli przynajmniej jedna z granic jednostronnych funkcji
f w
tym punkcie nie istnieje.
Twierdzenie
( Weierstrassa)
Jeżeli funkcja
f : [ a, b] → R jest ciągła, to jest ograniczna.
Ponadto wówczas istnieją takie argumenty
c 1 , c 2 ∈ [ a, b] , że
f ( c 1) jest najmniejszą wartością funkcji, a f ( c 2) - największą.
Twierdzenie
( Darboux o przyjmowaniu wartości pośrednich)
Jeżeli funkcja f : [ a, b] → R jest ciągła oraz f ( a) 6= f ( b) , to dla każdego w ∈ ( f ( a) , f ( b) ) istnieje c ∈ ( a, b) takie, że f ( c) = w.
Twierdzenie
( Darboux o miejscach zerowych funkcji)
Jeżeli funkcja f : [ a, b] → R jest ciągła oraz f ( a) · f ( b) < 0 , to istnieje c ∈ ( a, b) takie, że
f ( c) = 0 .
Przykład Wyznacz z dokładnościa do 0 , 1 przybliżenie pierwiastka wielomianu f ( x) = x 4 − 2 x − 1 zawartego w przedziale [ − 1 , 0] .