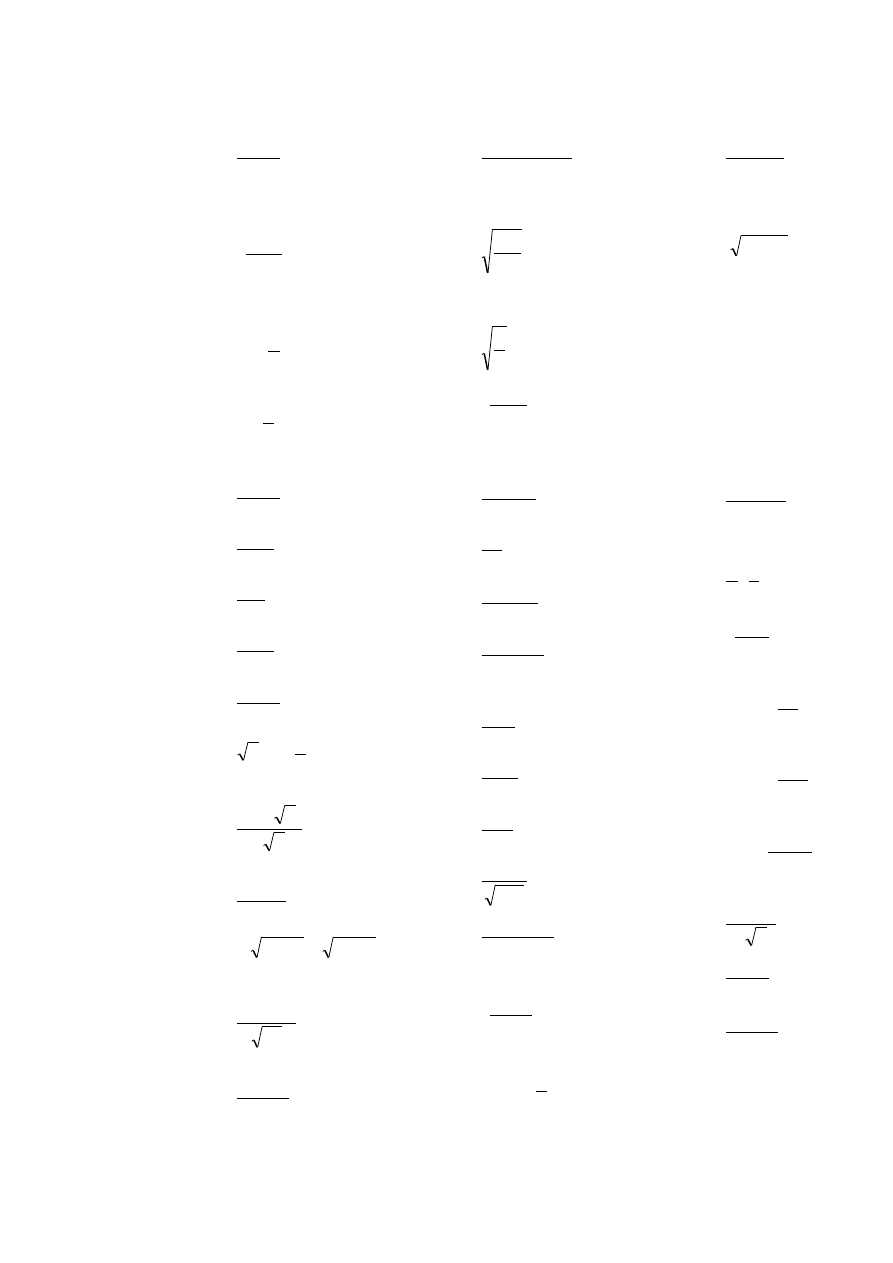
Lista zadań nr 3.

Strona 1 z 1

3. SZEREGI LICZBOWE.
3.1. Korzystając z definicji, wykazać zbieżność:

a)









2

2

1

1

n

n

b)

















1

2

1

1

n

n

n

c)













1

2

1

n

n

n

3.2. Sprawdź, które z następujących szeregów spełniają warunek konieczny zbieżności:

a)

n

n

n

n

















 

1

3

b)







1

100

1

n

n

c)















1

2

n

n

n

n

3.3. Uzasadnić, że szeregi są rozbieżne:

a)

















 

1

2

1

n

n

n

b)







1

1

cos

n

n

c)







1

1

n

n

n

d)























1

3

2

n

n

n

n

3.4. Zbadać zbieżność szeregów:

a)









1

1

2

1

n

n

b)







1

3

log

n

n

n

c)







2

ln

1

n

n

d)







1

2

log

n

n

n

e)







1

3

3

sin

n

n

n

f)







1

2

1

sin

n

n

n

g)

 







1

sin

n

n

n

n

n

h)







1

2

n

n

arctgn

i)

















1

2

2

1

1

n

n

n

n

j)













1

3

2

1

ln

n

n

n

k)











1

3

1

2

2

n

n

n

l)









1

6

2

3

n

n

n

n

m)







1

!

n

n

n

n

n)













1

3

!

1

2

7

n

n

n

o)

















1

2

3

2

5

1

n

n

n

n

n

p)









1

!

1

n

n

n

q)







1

100

!

n

n

n

r)







1

!

3

n

n

n

n

n

s)









1

3

3

4

n

n

n

n

t)













1

1

2

2

3

n

n

n

n

u)























1

2

1

3

n

n

n

n

v)



















1

1

arcsin

n

n

n

w)













1

2

2

1

3

n

n

n

n

n

n

x)



















1

5

3

1

n

n

n

y)





























1

1

1

1

n

n

n

n

n

z)

 











1

2

1

1

1

n

n

n

aa)

 











1

1

2

1

1

n

n

n

n

bb)

 













1

3

3

2

1

n

n

n

n

cc)







1

cos

n

n

n

n



dd)

 











1

1

3

1

n

n

n

ee)

 











2

1

log

1

n

n

n