
OBWODY ELEKTRYCZNE
i
Teoria Obwodów 1
Kurs powtórkowy
Kurs powtórkowy
Sierpie
ń
2011
Sierpie
ń
2011
w2
w2

Obwody elektryczne
• Analiza obwodu – zajmuje si
ę
poszukiwaniem
napi
ęć
i pr
ą
dów w poszczególnych cz
ęś
ciach
obwodu przy danych parametrach elementów i
schemacie obwodu
• Synteza obwodu – zajmuje si
ę
poszukiwaniem
schematu obwodu i parametrów elementów,
przy których mo
ż
na uzyska
ć
dane napi
ę
cia lub
pr
ą
dy przy danych niektórych napi
ę
ciach lub
pr
ą
dach w okre
ś
lonych cz
ęś
ciach obwodu.

Obwody SLS
1
1
2
2
( )
( )
( )
( )
x t
y t
x t
y t
→
→
⇔
Obwody: stacjonarne, liniowe , o parametrach skupionych
Własno
ś
ci:
Liniowo
ść
obwodu
Obwód elektryczny nazywamy liniowym je
ż
eli jest on utworzony z elementów
liniowych. Obwód ten spełnia warunki jednorodno
ś
ci i addytywno
ś
ci:
Je
ż
eli dla : obwód jest liniowy
;
gdzie a i b – dowolne warto
ś
ci stałe.
Zasada superpozycji: odpowied
ź
obwodu liniowego na jednoczesne działanie kilku
wymusze
ń
jest równa sumie odpowiedzi na ka
ż
de wymuszenie z osobna.
⇓
1
2
1
2
( )
( )
( )
( )
ax t
bx t
ay t
by t
+
=
+

Obwody SLS
1
1
1
1
( )
( )
(
)
(
)
x t
y t
x t
b
y t
b
→
⇒
+ →
+
Stacjonarno
ść
obwodu
Obwód zło
ż
ony z elementów liniowych jest stacjonarny je
ś
li:
gdzie b – dowolna stała warto
ść
Przyczynowo
ść
obwodu
je
ś
li dla t < b x(t)=0, to dla t < b y(t)=0;
gdzie b - dowolna stała warto
ść
.
Reakcja obwodu nie mo
ż
e nast
ą
pi
ć
przed jego pobudzeniem.
Pasywno
ść
obwodu
Obwód zło
ż
ony z elementów pasywnych liniowych jest zaliczany do obwodów
pasywnych.
Obwód o parametrach skupionych
Je
ż
eli rozmiary obwodu s
ą
małe w porównaniu z długo
ś
ci
ą
fali elektromagnetycznej
sygnału to wówczas mówimy, ze obwód ma skupione elementy ( parametry ) –
pomijamy rozmiary geometryczne elementu.

Sygnały
Wielko
ś
ci fizyczne zmienne, zale
ż
ne od czasu, takie jak u(t), i(t) nazywamy sygnałami.
Klasyfikacja sygnałów:
- nieokresowe
-okresowe ( sinusoidalne, przemienne, t
ę
tni
ą
ce , szczególny przypadek DC)
Nieokresowe:
- jednokierunkowe
-zmiennokierunkowe
- wykładnicza malej
ą
ca
- wykładnicza rosn
ą
ca
- specjalne:
- sygnał jednostkowy
- sygnał impulsowy
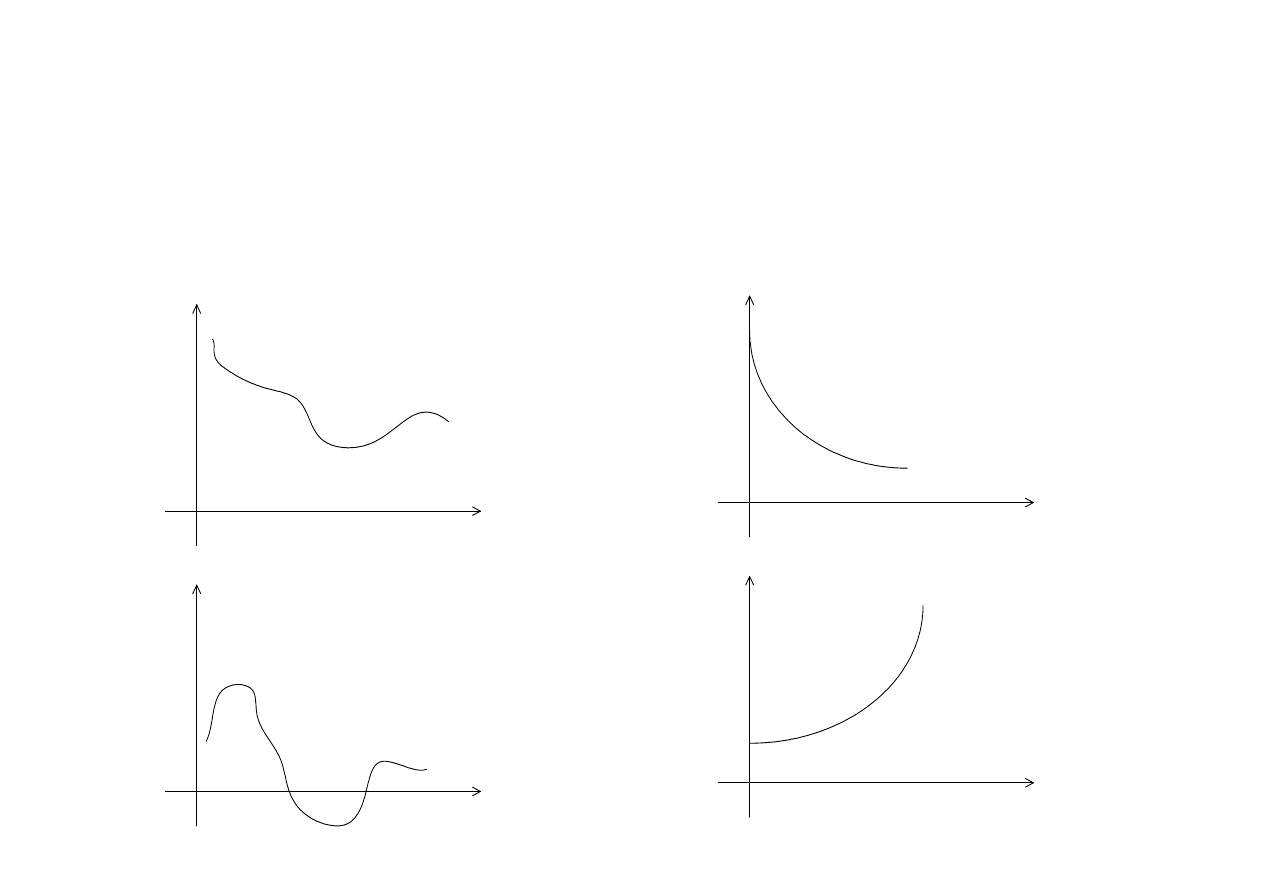
Sygnały
( )
f t
t
( )
f t
t
( )
f t
t
( )
f t
t
at
e
−
at
e
- jednokierunkowe
- zmiennokierunkowe
- wykładnicza malej
ą
ca
- wykładnicza rosn
ą
ca
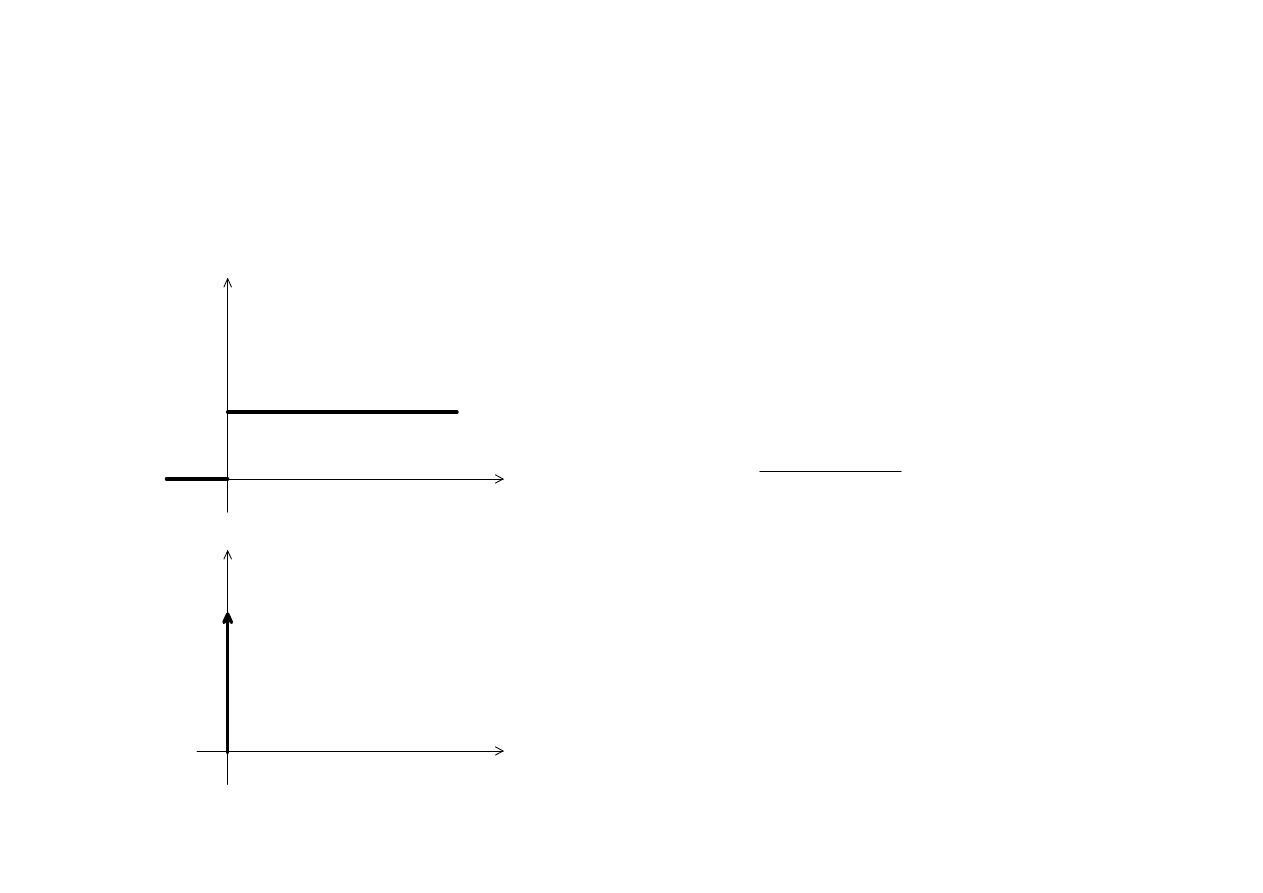
Sygnały
( )
f t
t
( )
f t
t
1
( )
t
ε
( )
t
δ
0
0
( )
1( )
1
0
dla
t
t
t
dla
t
ε
<
=
=
≥
0
( )
(
)
( , )
,
( )
lim
( , )
a
t
t
a
t a
t
t a
a
ε
ε
δ
δ
δ
→
−
−
=
=
- sygnał jednostkowy
- sygnał impulsowy
0
0
( )
0
dla
t
t
dla
t
δ
≠
=
∞
=
( )
1
t dt
δ
+∞
−∞
=
∫
Impuls Dirac’a
własno
ść

Sygnały okresowe
( )
f t
t
( )
f t
t
T
T
tętniąca
pulsująca
−
przemienna
0
0
( )
0
t
T
t
f t dt
+
≠
∫
0
0
( )
0
t
T
t
f t dt
+
=
∫
Okresowe: f(t+T)=f(t)
( )
f t
t
( )
f t
t
T
T
symetryczna
antysymetryczna
(
)
( )
2
T
f t
f t
+
= −
(
)
( )
2
T
f t
f t
+
=
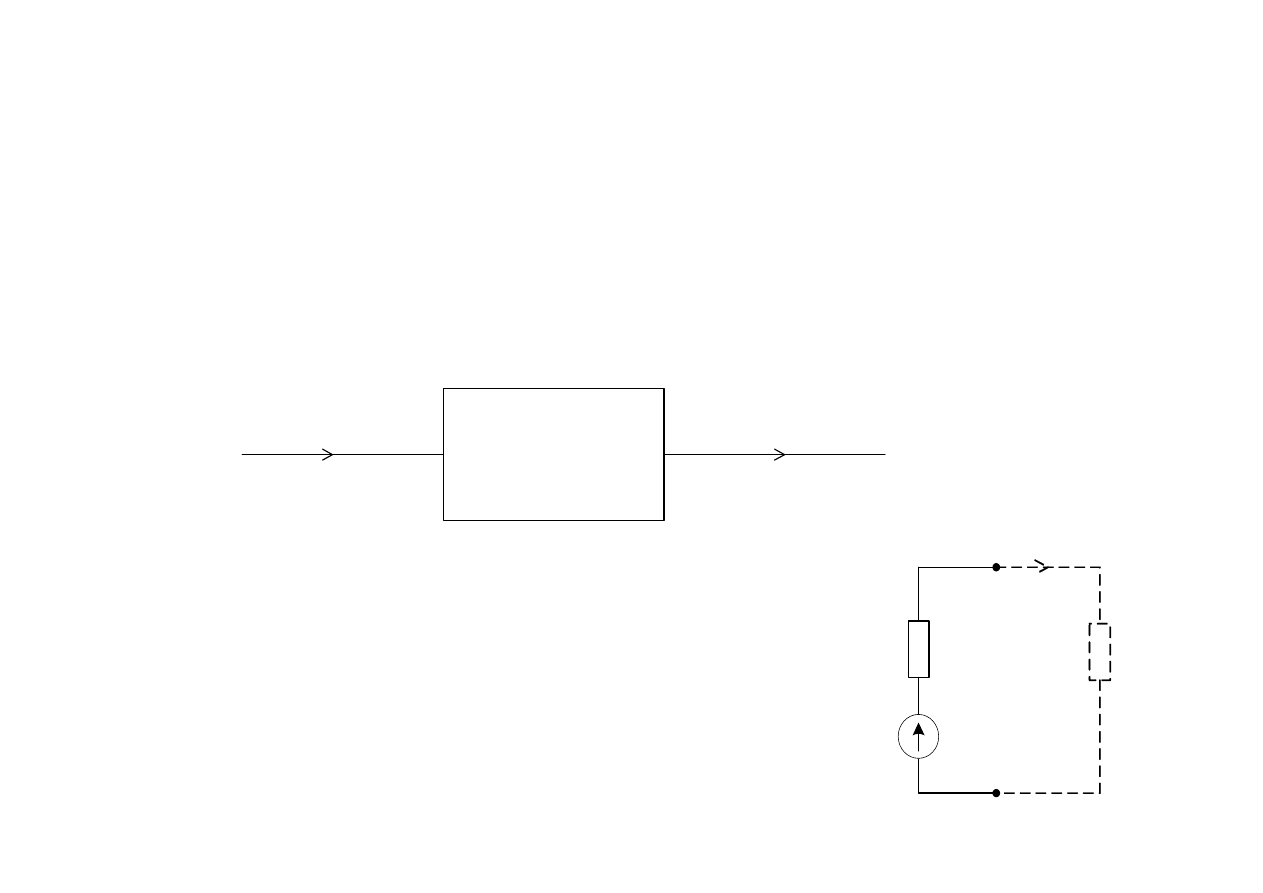
Obwody elektryczne
( )
x t
wejscie
( )
y t
wyjscie
SLS
( )
e t
( )
i t
w
R
o
R
Napi
ę
cia i pr
ą
dy wymuszone przez
ź
ródła energii nazywa si
ę
wymuszeniem i oznacza
x(t).
Reakcja na wymuszenie nazywa si
ę
odpowiedzi
ą
i oznacza y(t).
Schematycznie układ o jednym wej
ś
ciu i wyj
ś
ciu
przykład:
ź
ródło niesterowalne napi
ę
cia
wymuszenie – e(t); odpowied
ź
– i(t)
W zło
ż
onej sieci wymuszeniem mo
ż
e by
ć
zbiór wszystkich
ź
ródeł a odpowiedzi
ą
zbiór pr
ą
dów we wszystkich gał
ę
ziach.
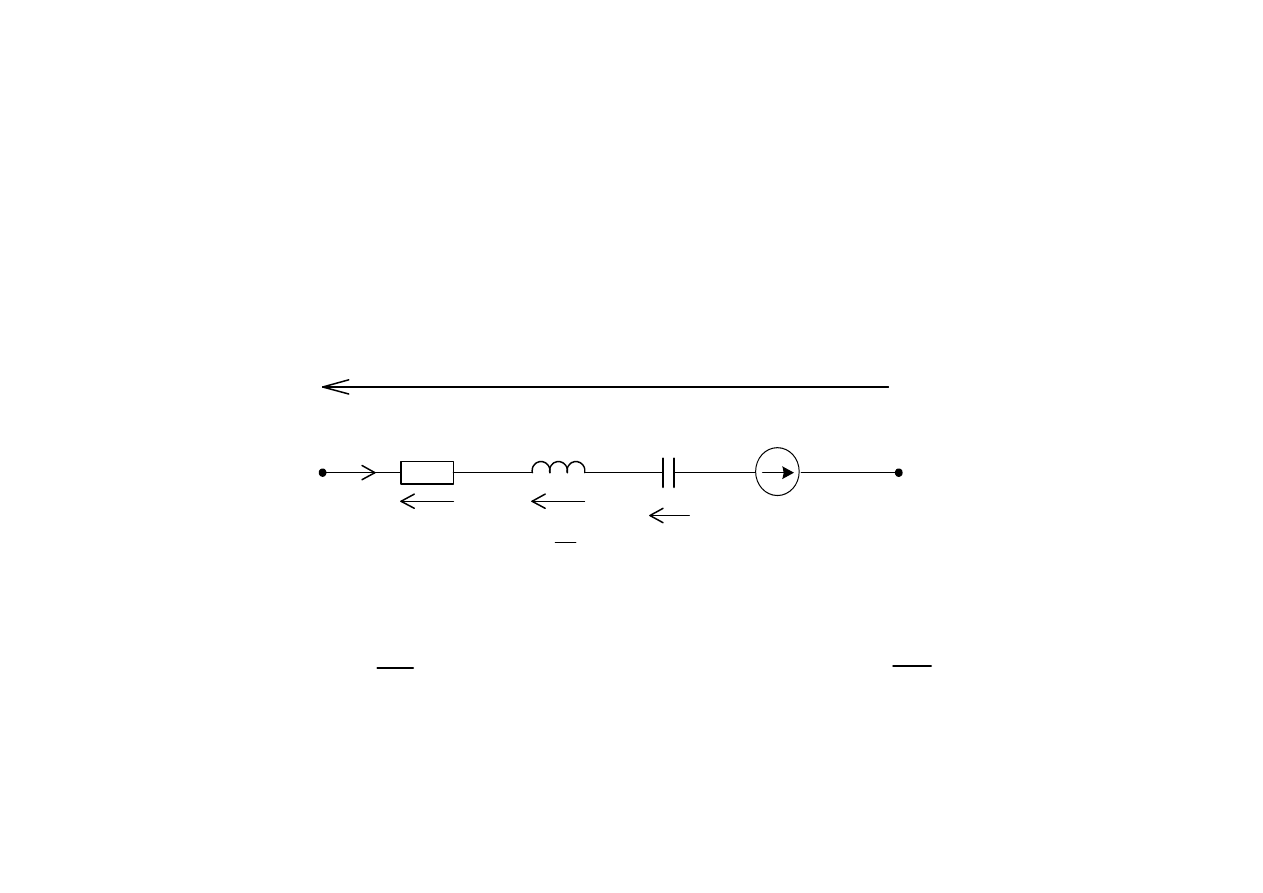
Obwody elektryczne
( )
e t
D idt
∫
di
L
dt
Ri
( )
i t
( )
u t
di
u
Ri
L
D idt
e
dt
=
+
+
−
∫
W obwodach elektrycznych stało
ść
parametrów R, L, C zapewnia liniowo
ść
,
stacjonarno
ść
i przyczynowo
ść
.
Prawo Ohma
dla gał
ę
zi szeregowej RLC ma posta
ć
:
1
D
C
=
gdzie
Obwody elektryczne
1
1 1
1
1
1
1
1
1
1
1 1
j
j
j j
j
j
j j
j
j
j
j
n
n n
n
n
n
n n
n
n
n
n
di
d
R i
L
D i dt
e
L
i
dt
dt
u
R i
di
d
u
R i
L
i
R i
L
D
i dt
e
dt
dt
u
R i
d
di
L
i
R i
L
D
i dt
e
dt
dt
+
+
−
⋅
⋅
⋅
⋅
=
=
+
+
+
+
−
⋅
⋅
⋅
⋅
+
+
−
∫
∫
∫
1
1
1
j
j
j
n
n
n
D i dt
e
D
i dt
e
e
D
i dt
⋅
⋅
−
⋅
⋅
∫
∫
∫
1
1
1
1
1
1
1
0
0
0
0
0
0
j
j
j
j
j
j
j
n
n
n
n
n
n
n
R
i
L
i
D
i
e
d
R
i
L
i
D
i dt
e
dt
R
i
L
i
D
i
e
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
+
+
−
⋅
⋅
⋅
⋅
⋅
⋅
⋅
∫
w zapisie macierzowym dla n gał
ę
zi
[ ] [ ][ ] [ ] [ ] [ ] [ ] [ ]
d
U
R I
L
I
D
I dt
E
dt
=
+
+
−
∫
czyli

Prawo Ohma
[ ] [ ] [ ]
[ ]
[ ] [ ]
{
}
d
U
R
L
D
dt
I
E
dt
=
+
+
−
∫
lub umownie
Jest to rozszerzona posta
ć
prawa Ohma dla gał
ę
zi obwodu liniowego i stacjonarnego.
- ł
ą
cznie n równa
ń
dla n gał
ę
zi.
Georg Simon Ohm (ur. 16.03.1789 w Erlangen, zm.
8.07.1854 w Monachium matematyk niemiecki,
profesor politechniki w Norymberdze w latach 1833=
1849 i uniwersytetu w Monachium po roku 1949 .
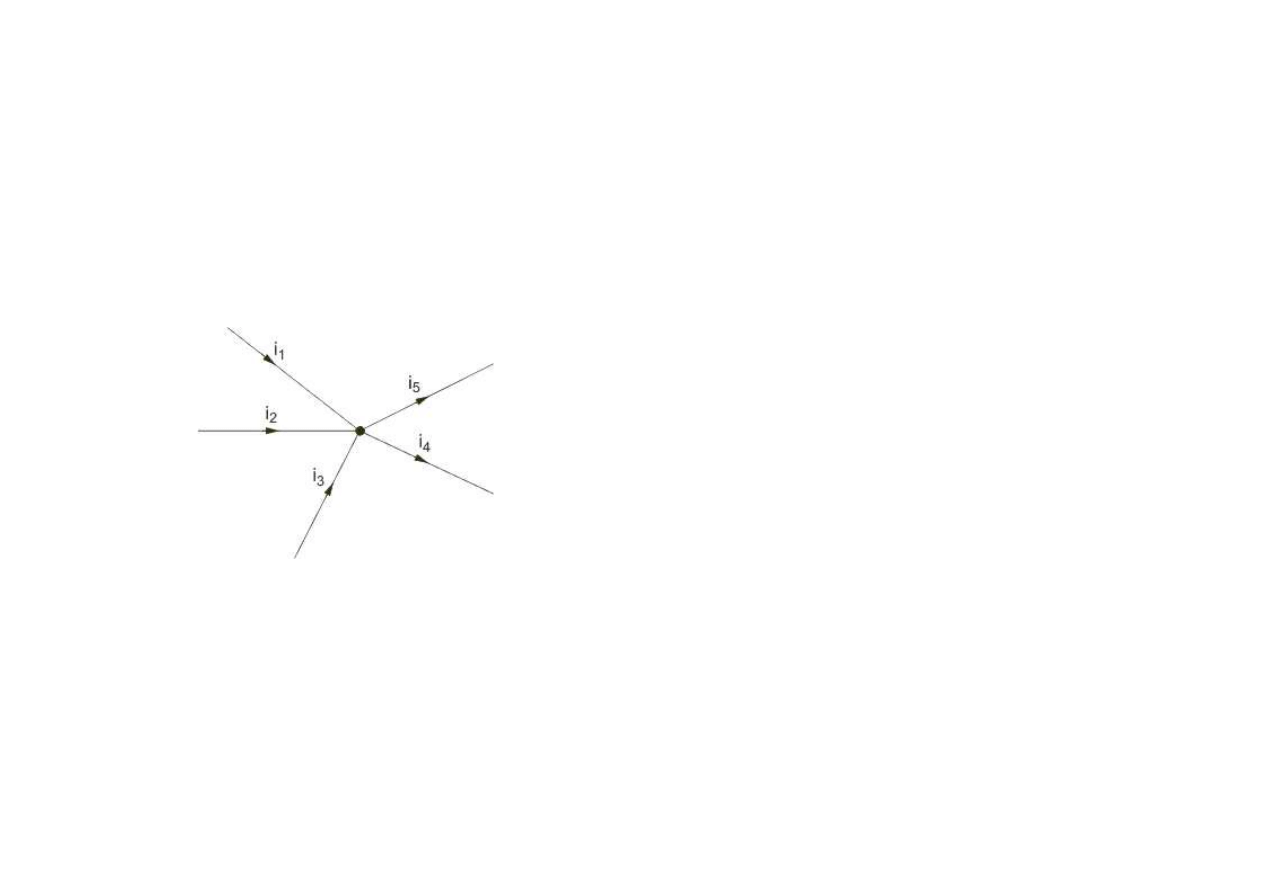
Prawa Kirchhoffa
1
2
3
4
5
0
i
i
i
i
i
+ + − − =
Pr
ą
dowe prawo Kirchhoffa (w
ę
złowe, pierwsze ) –
PPK
Jest ono wynikiem prawa zachowania ładunku i jego przepływu stacjonarnego ładunku.
1
2
3
4
5
0 / :
q
q
q
q
q
dt
∆ + ∆ + ∆ − ∆ − ∆ =
st
ą
d
0
j
węzle
i
± =
∑
Umowa – pr
ą
dy do w
ę
zła z +
czyli
Suma algebraiczna pr
ą
dów w w
ęź
le równa jest zeru.

Prawa Kirchhoffa
1
1
0
kj
gdy
galaz
zorientowana
na
zewnatrz
wezla
a
gdy
galaz
zorientowana
do
wezla
gdy
galaz
nie
jest
skorelowana
z
wezlem
+
= −
[ ]
11
1
1
1
1
1
1
j
n
k
kj
kn
w
wj
wn
galaz
j
n
wezel
a
a
a
A
k
a
a
a
w
a
a
a
⋅
⋅
⋅
=
⋅
Wygodnie jest wykorzysta
ć
wyrazy macierzy w
ę
złowej
Macierz incydencji w
ę
złowa
gdzie n – liczba gał
ę
zi a w – liczba w
ę
złów niezale
ż
nych ( o jeden mniej o liczby
wszystkich w
ę
złów w obwodzie ).
Prawa Kirchhoffa
( )
0
kj j
węzel k
a i
=
∑
[ ][ ] [ ]
0
A I
=
1
11
1
1
1
1
1
0
1
0
0
0
0
j
n
j
k
kj
kn
n
w
wj
wn
galaz
j
n
i
wezel
a
a
a
i
k
a
a
a
i
w
a
a
a
⋅
⋅
⋅
⋅
⋅
=
⋅
⋅
dla k – tego w
ę
zła
a w zapisie macierzowym
z PPK otrzymujemy tyle równa
ń
ile jest w
ę
złów niezale
ż
nych ( w ).
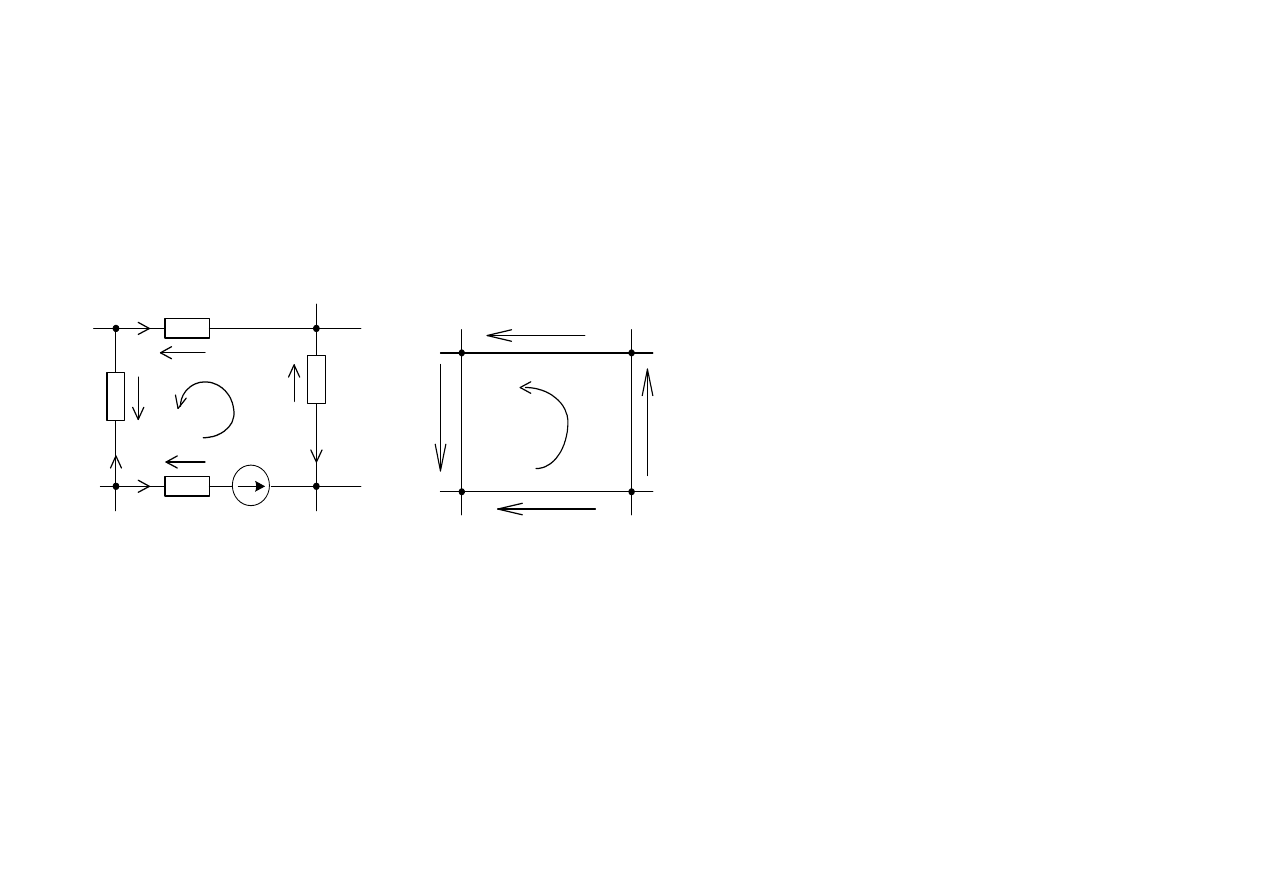
Prawa Kirchhoffa
1
u
2
u
3
u
4
u
4
E
1
u
2
u
3
u
4
u
1
V
2
V
3
V
4
V
1
2
3
4
0
u
u
u
u
+ + − =
(
) (
) (
) (
)
1
2
2
3
3
4
1
4
0
V
V
V
V
V
V
V
V
−
+
−
+
−
−
−
=
0
j
oczko
u
± =
∑
Napi
ę
ciowe prawo Kirchhoffa ( oczkowe, drugie ) –
NPK
Jest ono wyrazem potencjalno
ś
ci .
Dla dowolnego oczka przy przyj
ę
tej orientacji
Czyli w oczku

Prawa Kirchhoffa
1
1
0
kj
gdy
zgodnie
b
gdy
przeciwnie
brak
korelacji
+
= −
[ ]
11
1
1
1
1
1
1
j
n
k
kj
kn
m
mj
mn
galaz
j
n
oczko
b
b
b
B
k
b
b
b
m
b
b
b
⋅
⋅
⋅
=
⋅
( )
0
kj
j
oczko k
b u
=
∑
Wygodnie jest wykorzysta
ć
wyrazy macierzy oczkowej
Macierz incydencji oczkowa
m= n-w liczba oczek niezale
ż
nych
zgodnie z tym mo
ż
emy zapisa
ć

Prawa Kirchhoffa
[ ] [ ] [ ]
0
B
U
⋅
=
[ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ]
0
0
T
B
U
B
A
V
V
⋅
=
⋅
=
⋅
=
[ ] [ ] [ ]
T
U
A
V
=
napi
ę
cia gał
ę
zi mo
ż
na wyrazi
ć
równaniem
gdy
ż
mo
ż
na pokaza
ć
,
ż
e
[ ][ ] [ ]
0
T
B A
=
NPK – m równa
ń
niezale
ż
nych

Prawa Kirchhoffa
Gustav Robert Kirchhoff (ur. 12.03.1824 w Królewcu,
zm. 17.10.1887 w Berlinie) –niemiecki fizyk.
Podsumowanie:
n – równa
ń
na prawo Ohma
w – równa
ń
na PPK
m – równa
ń
na NPK
To
n + w + m = 2n równa
ń
dla 2n niewiadomych ( uj,ij ).

Bilans mocy
[ ] [ ] [ ] [ ] [ ] [ ] [ ][ ] [ ] [ ] [ ]
1
1
1
0
0
0
n
T
T
T
T
T
j j
j
n
j
j
n
i
u i
u
u
u
i
U
I
A
V
I
V
A I
V
i
=
⋅
=
⋅
⋅
=
=
=
=
=
=
⋅
∑
1
0
n
j j
j
u i
=
=
∑
Bilans mocy w układzie elektrycznym
Suma mocy pobieranych przez wszystkie gał
ę
zie obwodu
czyli
suma mocy chwilowych pobieranych przez wszystkie gał
ę
zie obwodu jest równa zero.
Niektóre gał
ę
zie s
ą
ź
ródłami energii i dla tych gał
ę
zi u
k
i
k
< 0.
W gał
ę
ziach pobieraj
ą
cych energi
ę
w danej chwili u
k
i
k
> 0.

Obwody elektryczne
Klasyfikacja obwodów
Ze wzgl
ę
du na liniowo
ść
- liniowe, spełniaj
ą
zasad
ę
superpozycji
i nieliniowe, nie spełniaj
ą
zasady superpozycji
Obwód jest liniowy gdy wszystkie jego elementy s
ą
liniowe.
Obwód zawieraj
ą
cy przynajmniej jeden element nieliniowy jest obwodem
nieliniowym.
Ź
ródło napi
ę
cia jest liniowe, je
ż
eli jego napi
ę
cie
ź
ródłowe oraz rezystancja i
indukcyjno
ść
wewn
ę
trzna nie zale
żą
od płyn
ą
cego przez nie pr
ą
du.
W układzie SLS przy zasilaniu napi
ę
ciem stałym ( DC ) ( lub pr
ą
dem stałym ze
ź
ródła pr
ą
dowego ) przez pewien czas po zał
ą
czeniu zasilania przebiegi
zmieniaj
ą
si
ę
w czasie . Po pewnym czasie ustala si
ę
stan równowagi mi
ę
dzy
energi
ą
zasilania a energi
ą
rozpraszan
ą
na rezystorach. Ustalaj
ą
si
ę
warto
ś
ci
stałe napi
ęć
i pr
ą
dów na wszystkich elementach obwodu. Mówimy, ze wyst
ą
pił
stan ustalony w obwodzie.
Przy zasilaniu okresowym ,
Po pewnym czasie równie
ż
ustalaj
ą
si
ę
przebiegi okresowe na wszystkich
elementach obwodu SLS. Dla nast
ę
puje stan ustalony ( a praktycznie
dla t > 5
τ
)
t
→ ∞

Obwody elektryczne
2
2
0
0
0
0
T
T
T
T
W
pdt
uidt
Ri dt R i dt
=
=
=
=
∫
∫
∫
∫
2
2
2
0
0
T
T
s
s
s
W
RI dt RI
dt
RI T
=
=
=
∫
∫
2
0
1
T
s
I
i dt
T
=
∫
Pr
ą
d przepływaj
ą
c przez opornik liniowy R wywołuje skutki cieplne ( prawo
Joul’a – Lenza )
Np. w okresie T wydziela energi
ę
w postaci ciepła
Tak
ą
sam
ą
ilo
ść
energii w czasie T na oporniku R wydzieli pr
ą
d stały o o
odpowiednio dobranej warto
ś
ci Is.
st
ą
d
Jest to tzw. warto
ść
skuteczna pr
ą
du zmiennego okresowo.
Warto
ś
ci
ą
skuteczn
ą
pr
ą
du okresowego nazywamy tak
ą
warto
ść
pr
ą
du stałego ,
który przepływaj
ą
c przez niezmienny rezystor R wydzieli w czasie okresu T tak
ą
sam
ą
ilo
ść
ciepła ciepła co pr
ą
d okresowy w tym samym czasie.

Obwody elektryczne
2
0
1
T
s
F
f dt
T
=
∫
2
2
2
2
2
2
2
0
0
0
0
1
1
1
sin (
)
sin (
)
[
cos(2
2
)]
2
2
2
T
T
T
T
m
i
m
i
m
i
m
f dt
F
t
dt
F
t
dt
F
t
dt
TF
ω
ω
ω
=
+ Ψ
=
+ Ψ
=
−
+ Ψ
=
∫
∫
∫
∫
2
2
1 1
(
)
0, 707
2
2
2
m
m
s
s
m
F
F
F
TF
F
T
=
=
=
=
2
1, 41
m
sz
s
F
k
F
=
=
=
Dla dowolnego sygnału okresowego w ten sposób definiuje si
ę
warto
ść
skuteczn
ą
, chocia
ż
nie ma ona ju
ż
takiej interpretacji fizycznej.
W przypadku sygnału sinusoidalnego obliczamy
a wi
ę
c
cz
ę
sto F
s
oznaczamy jako F
współczynnik szczytu
Obwody elektryczne
0
1
T
sr
F
fdt
T
=
∫
2
1 2
0
0
1
2
T
T
sr
F
f dt
fdt
T
T
=
=
∫
∫
2
2
1
0
2
0
2
2
4
2
2
sin
cos
( 1 1)
0, 636
2
T
T
m
m
m
m
m
m
sr
F
F
F
F
F
F
tdt
t
F
T
T
T
ω
ω
ω
ω
=
= −
= −
− − =
=
=
Π
Π
∫
2
2
2
1,11
2
4
m
k
m
sr
F
F
k
F
F
Π
=
=
=
=
Π
dla przebiegów okresowych wprowadza si
ę
warto
ść
ś
redni
ą
( algebraiczn
ą
)
Dla przebiegów przemiennych F
sr
=0, dlatego wprowadza si
ę
poj
ę
cie warto
ś
ci
ś
redniej przebiegu wyprostowanego ( lub warto
ść
ś
redni
ą
połówkow
ą
).
W przypadku sygnału sinusoidalnego obliczamy
współczynnik kształtu

sygnały harmoniczne
( )
sin(
)
m
f t
F
t
ω
=
+ Ψ
sygnały harmoniczne podgrupa przebiegów okresowych przemiennych i
symetrycznych okre
ś
lona poprzez funkcj
ę
sinus
w technice wytwarzania i przesyłu i rozdziału energii elektrycznej
wyst
ę
puje bardzo cz
ę
sto ze wzgl
ę
du na :
- łatwo
ść
wytwarzania ( generatory napi
ę
cia przemiennego )
- powtarzanie kształtu w stanie ustalonym
- łatwo
ść
analizy przy zastosowaniu metody symbolicznej.
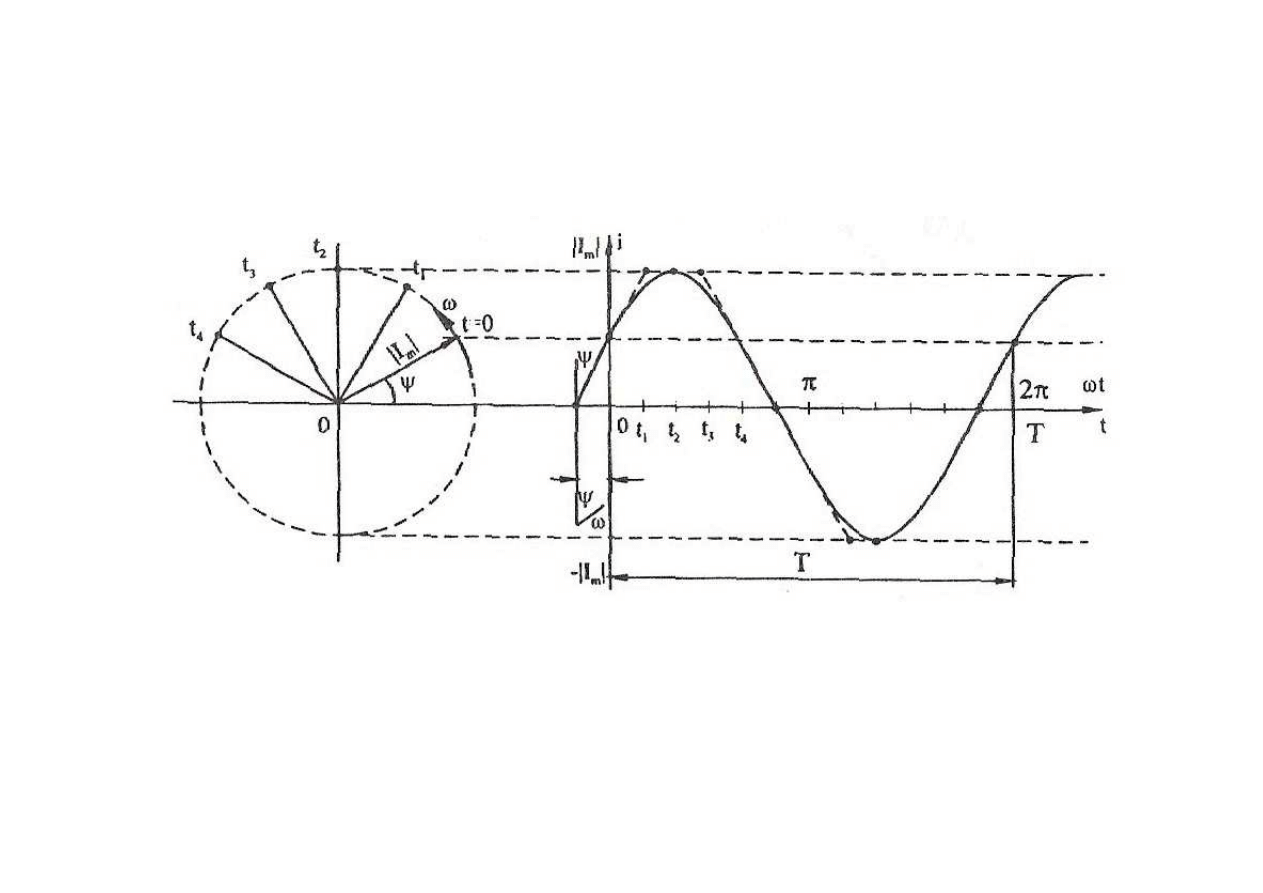
Wskaz wiruj
ą
cy
•
( )
sin(
)
m
i t
I
t
ω
=
+ Ψ
Rzut wskazu wiruj
ą
cego na o
ś
pionow
ą
jest przebiegiem chwilowym
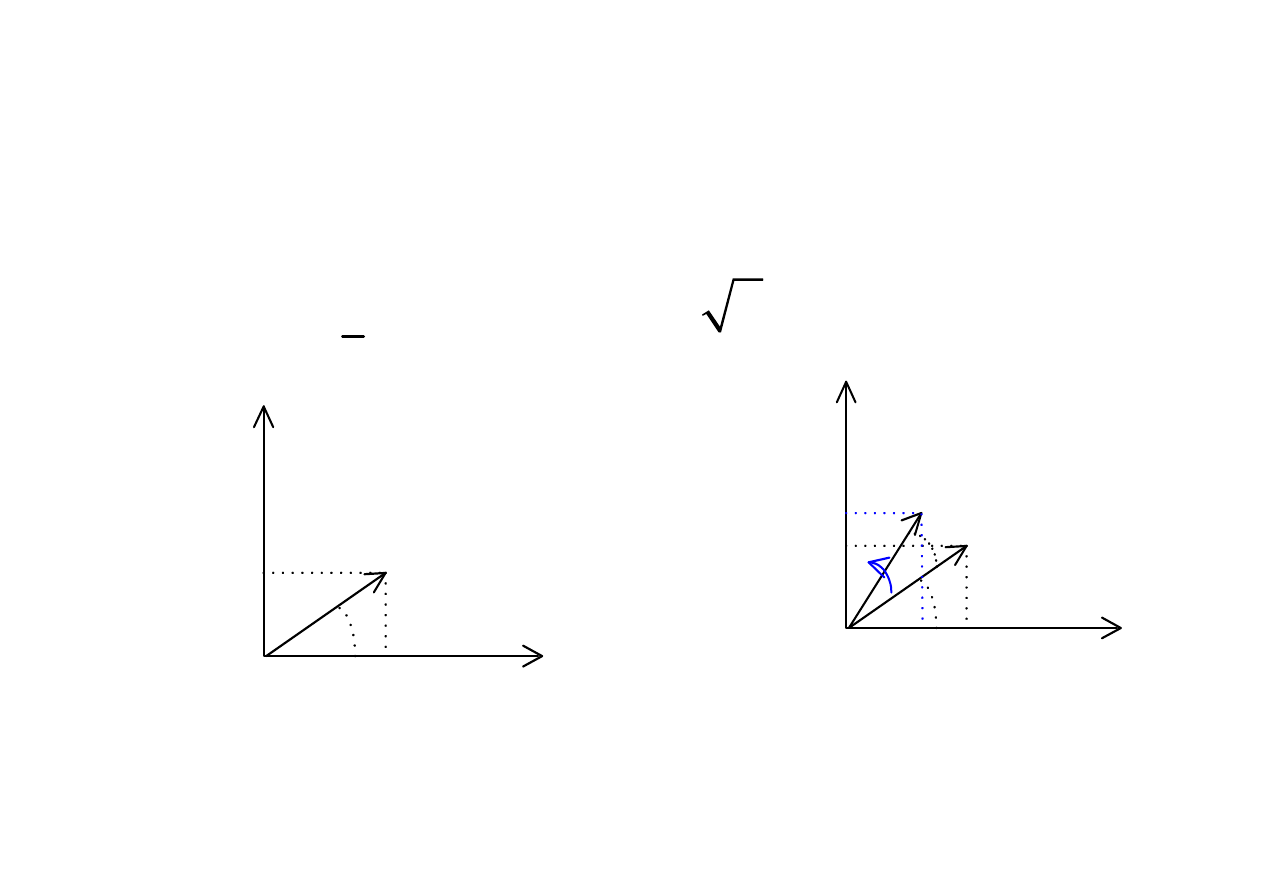
Wskaz wiruj
ą
cy
(
)
( )
2
t
j
j
j
t
m
I t
I e e
Ie
ω
ω
Ψ
+Ψ
=
=
Re
Im
Ψ
j
m
I e
Ψ
cos
m
I
Ψ
sin
m
I
Ψ
0
t
=
Re
Im
Ψ
(
)
j
t
m
I e
ω
+Ψ
cos(
)
m
I
t
ω
+Ψ
sin(
)
m
I
t
ω
+Ψ
0
t
≠
t
ω
Wskaz wiruj
ą
cy na płaszczy
ź
nie zespolonej mo
ż
e by
ć
zapisany w postaci
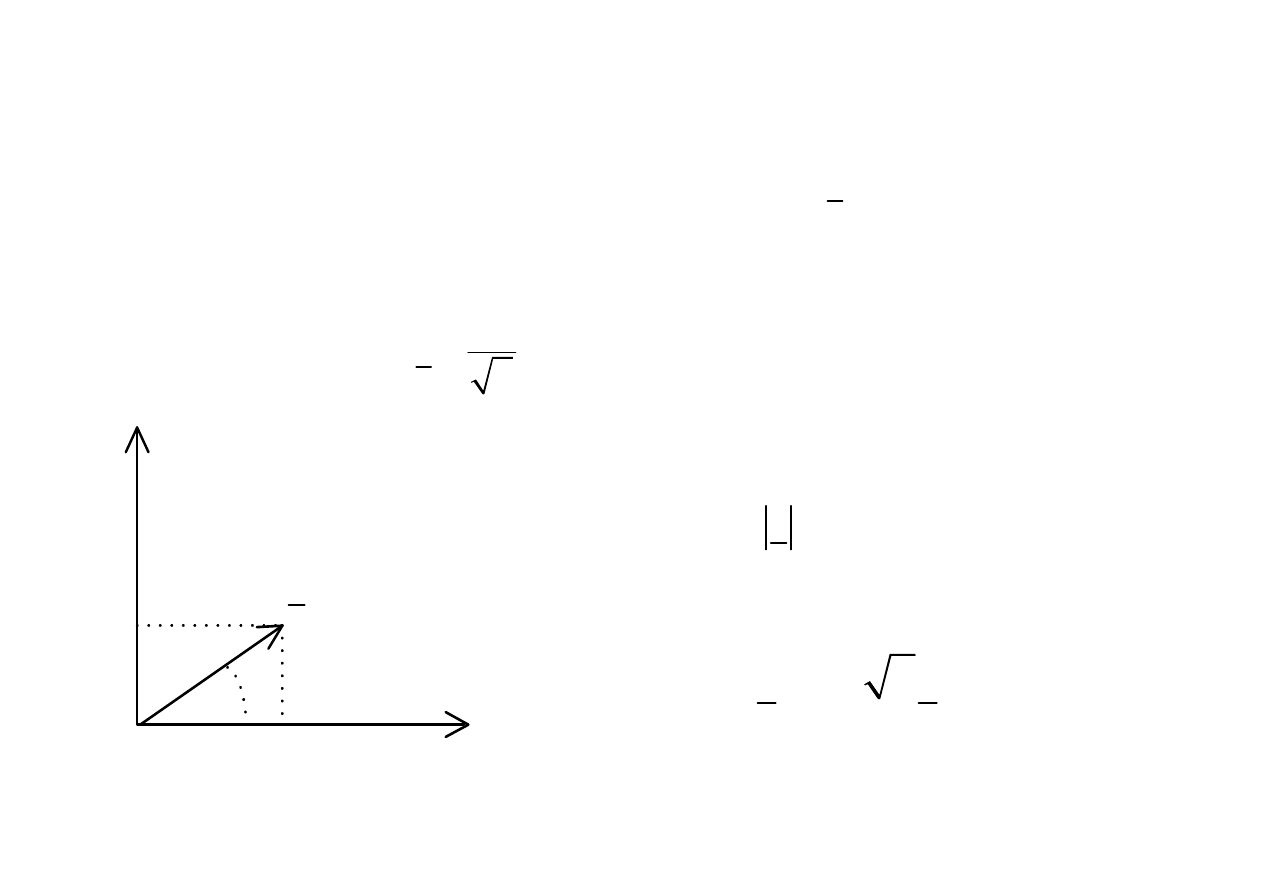
Obwody elektryczne
{ }
( )
Im
( )
sin(
)
m
i t
I t
I
t
ω
=
=
+ Ψ
2
j
j
m
I
I
e
Ie
Ψ
Ψ
=
=
Re
Im
Ψ
I
I
I
= →
Ψ →
( )
2
j t
I t
Ie
ω
=
jego cz
ęść
urojona jest przebiegiem pr
ą
du
Zwykle wskaz wiruj
ą
cy rysuje si
ę
w pozycji dla t=0
Liczb
ę
zespolon
ą
nazywa si
ę
warto
ś
ci
ą
zespolon
ą
przebiegu sinusoidalnego.
moduł
warto
ść
skuteczna
argument
faza pocz
ą
tkowa
Warto
ś
ci zespolone s
ą
powszechnie stosowane dla przebiegów harmonicznych w
elektrotechnice.

Liczby zespolone

Liczby zespolone

Liczby zespolone

Liczby zespolone

Liczby zespolone


Liczby zespolone
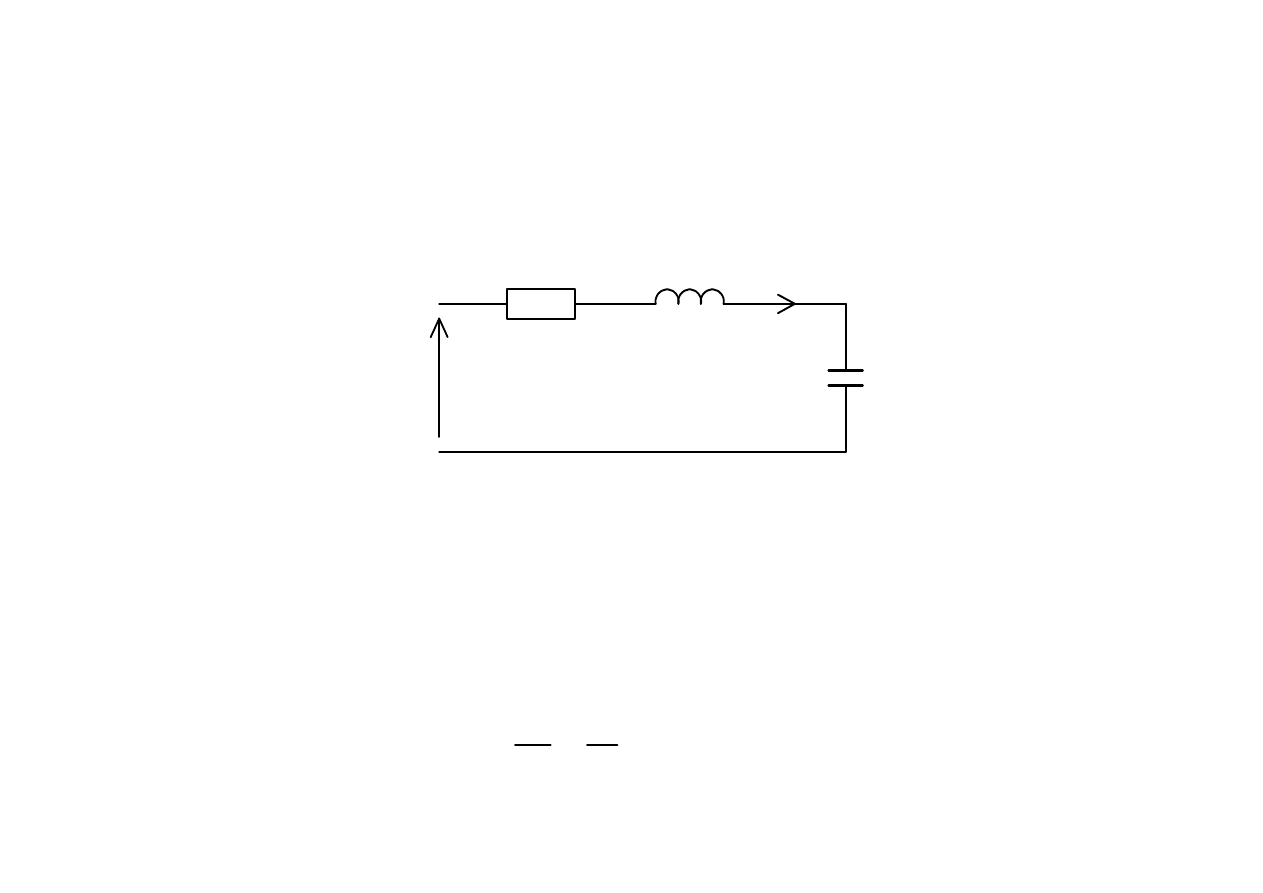
Metoda symboliczna
R
L
C
( )
sin(
)
m
u
u t
U
t
ω
=
+Ψ
( ) ?
i t
=
( )
( )
( )
( )
R
L
C
u t
u t
u t
u t
=
+
+
1
sin(
)
(*)
m
u
di
Ri
L
idt
U
t
dt
C
ω
+
+
=
+ Ψ
∫
Gał
ąź
szeregowa RLC ( warto
ś
ci stałe ) zasilana napi
ę
cie sinusoidalnym.
w stanie ustalonym równie
ż
pr
ą
d b
ę
dzie przebiegiem sinusoidalnym o tej samej pulsacji.
Dane: R, L, C, U
m
,
ω
,
ψ
u
Obliczyc : I
m
=?,
ψ
i
=?
Z NPK
czyli
Metoda symboliczna
{ }
{
}
( )
Im
( )
;
( )
Im
( )
i t
I t
u t
U t
=
=
{ }
{ }
{ }
{
}
{ }
{ }
{ }
{
}
1
Im
( )
Im
( )
Im
( )
Im
( )
lub
1
Im[
( )
( )
( )
]
Im
( )
d
R
I t
L
I t
I t
dt
U t
dt
C
d
R I t
L
I t
I t
dt
U t
dt
C
+
+
=
+
+
=
∫
∫
1
( )
( )
( )
( )
(**)
d
RI t
L
I t
I t dt
U t
dt
C
+
+
=
∫
podstawiamy
st
ą
d
je
ż
eli funkcje w nawiasach b
ę
d
ą
sobie równe to równie
ż
ich cz
ęś
ci urojone b
ę
d
ą
sobie równe
Metoda symboliczna
( )
;
( )
U t
I t
( )
2
j t
I t
Ie
ω
=
( )
2
( )
j t
d
I t
I j e
j I t
dt
ω
ω
ω
=
=
1
1
( )
2
( )
j t
I t dt
I
e
I t
j
j
ω
ω
ω
=
=
∫
1
( )
( )
( )
( )
RI t
j I t
I t
U t
j C
ω
ω
+
+
=
z tej równo
ś
ci wynika równo
ść
fizyczna (*)
Równo
ść
(**) jest zapisem równania obwodu dla funkcji zespolonych
zamiast funkcji czasu u(t) ; i(t).
Podstawiamy
st
ą
d równanie (**)
Metoda symboliczna
1
2
2
2
2
: 2
1
R
I
j
I
I
U
j C
RI
j I
I
U
j C
ω
ω
ω
ω
+
+
=
+
+
=
R
L
C
U
U
U
U
+
+
=
lub dla chwili t=0
sumowanie warto
ś
ci chwilowych odpowiada sumowaniu warto
ś
ci zespolonych !
całkowanie
→
dzielenie przez j
ω
ró
ż
niczkowanie
→
mno
ż
enie przez j
ω
Zapis zespolony napi
ęć
obwodu
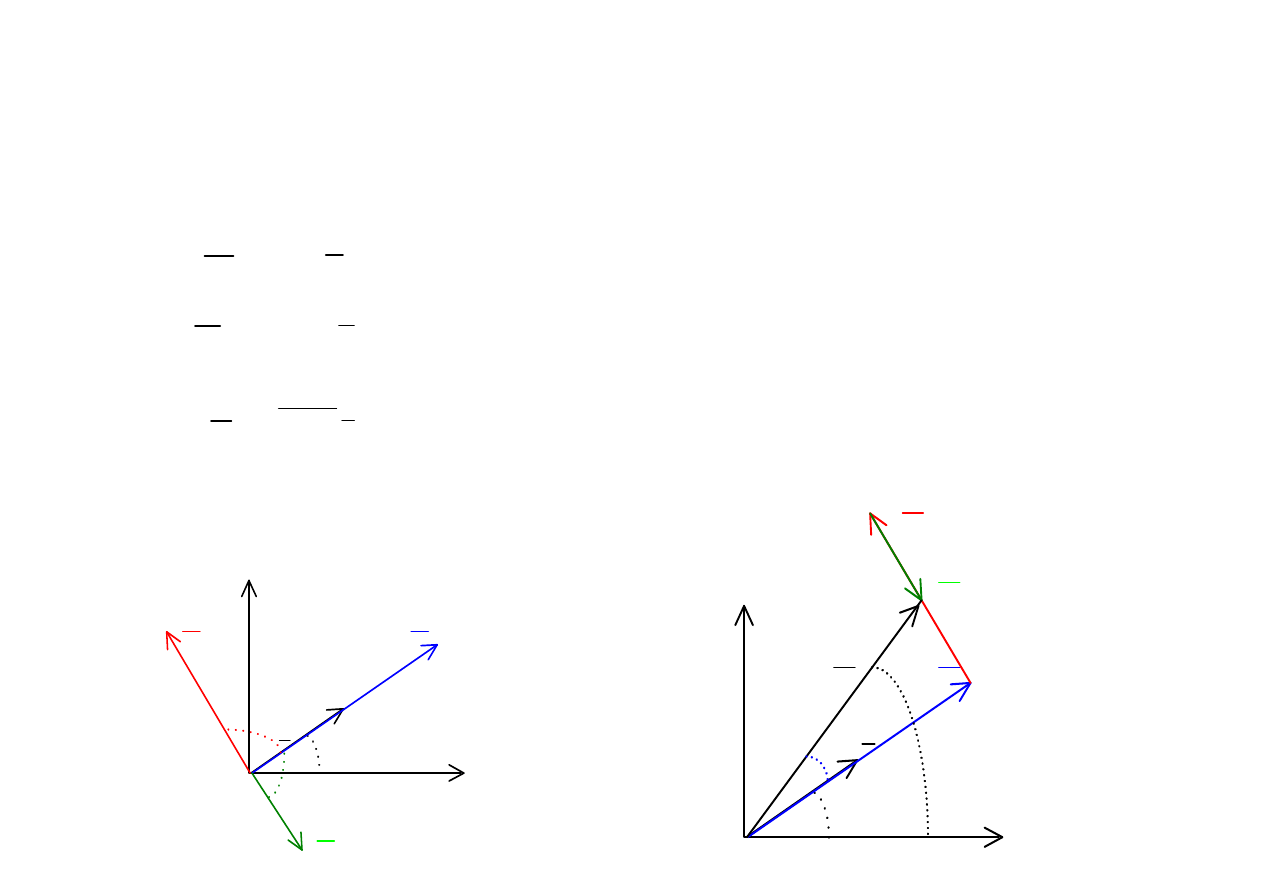
Metoda symboliczna
L
U
j LI
ω
=
1
C
U
I
j C
ω
=
Re
Im
I
I
Ψ
R
U
L
U
•
C
U
i
R
U
RI
=
Re
Im
I
I
Ψ
R
U
L
U
C
U
U
U
Ψ
ϕ
- warto
ść
zespolona napi
ę
cia na rezystorze R
- warto
ść
zespolona napi
ę
cia na cewce L
- warto
ść
zespolona napi
ę
cia na kondensatorze C
na płaszczy
ź
nie zespolonej

Metoda symboliczna
(
)
2
2
I
I
I
j
j
j
j
L
U
j LI
j Ie
LIe
e
LIe
ω
ω
ω
ω
Π
Π
Ψ +
Ψ
Ψ
=
=
=
=
(
)
2
2
1
1
1
1
I
I
I
j
j
j
j
C
U
I
j
Ie
Ie
e
Ie
j C
C
C
C
ω
ω
ω
ω
Π
Π
−
Ψ −
Ψ
Ψ
=
= −
=
=
(
)
2
2
I
I
I
j
j
j
j
L
U
j LI
j Ie
LIe
e
LIe
ω
ω
ω
ω
Π
Π
Ψ +
Ψ
Ψ
=
=
=
=
{
}
( )
Im
2
2
sin(
)
2
sin(
)
2
j t
L
I
L
uL
u t
U
e
LI
t
U
t
ω
ω
ω
ω
Π
=
=
+ Ψ +
=
+ Ψ
( )
sin(
)
m
I
i t
I
t
ω
=
+ Ψ
ω
L=XL
→
reaktancja indukcyjna cewki
1/
ω
C=XC
→
reaktancja pojemno
ś
ciowa kondensatora
Interpretacja wykresu dla przebiegów chwilowych
gdzie U
L
=
ω
LI ;
ψ
uL
=
ψ
I
+
Π
/2
i
I
L
U
Metoda symboliczna
( )
(
sin(
))
cos(
)
2
sin(
)
2
L
m
I
m
I
I
d
u t
L
I
t
LI
t
LI
t
dt
ω
ω
ω
ω
ω
Π
=
+ Ψ
=
+ Ψ =
+ Ψ +
bez u
ż
ycia licz zespolonych
2
uL
I
Π
Ψ − Ψ =
Napi
ę
cie na cewce idealnej wyprzedza pr
ą
d o k
ą
t
Π
/2 lub równowa
ż
nie pr
ą
d
opó
ź
nia si
ę
o k
ą
t
Π
/2.
Metoda symboliczna
(
)
2
2
1
1
1
1
I
I
I
j
j
j
j
C
U
I
j
Ie
Ie
e
Ie
j C
C
C
C
ω
ω
ω
ω
Π
Π
−
Ψ −
Ψ
Ψ
=
= −
=
=
(
)
2
1
1
( )
Im{ 2
}
Im{ 2
}
2
sin(
)
2
sin(
)
2
I
j
t
j t
C
C
I
C
uC
u t
U e
Ie
I
t
U
t
C
C
ω
ω
ω
ω
ω
ω
Π
+Ψ −
Π
=
=
=
+ Ψ −
=
+ Ψ
,
,
2
2
C
uC
I
uC
I
I
U
C
ω
Π
Π
=
Ψ = Ψ −
Ψ − Ψ = −
i
I
C
U
Warto
ść
zespolona napi
ę
cia na kondensatorze
gdzie
Napi
ę
cie na kondensatorze idealnym opó
ź
nia si
ę
wzgl
ę
dem pr
ą
du o kat
Π
/2 lub pr
ą
d wyprzedza
napi
ę
cie o kat
Π
/2.

Metoda symboliczna
I
j
R
U
RI
RIe
Ψ
=
=
(
)
1
( )
Im{ 2
}
Im{ 2
}
2
sin(
)
2
sin(
)
I
j
t
j t
R
R
I
R
uR
u t
U e
RIe
I
t
U
t
C
ω
ω
ω
ω
ω
+Ψ
=
=
=
+ Ψ =
+ Ψ
,
,
0
R
uR
I
uR
I
U
IR
=
Ψ = Ψ
Ψ − Ψ =
I
R
U
Warto
ść
zespolona napi
ę
cia na rezystorze
gdzie
Napi
ę
cie na rezystorze jest w fazie z pr
ą
dem.
Wyszukiwarka
Podobne podstrony:
Oe i To1 w10
Oe i To1 w12
Oe i To1 w5 id 333223 Nieznany
Oe i To1 w3 id 333221 Nieznany
Oe i To1 w7 magn sprz id 333225
Oe i To1 w1
Oe i To1 w9 id 333227 Nieznany
Oe i To1 w4 id 333222 Nieznany
Oe i To1 w6 id 333224 Nieznany
Oe i To1 w8
Oe i To1 w10
więcej podobnych podstron