T.1.

POMIARY

PARAMETRÓW

PRĄDU

STAŁEGO

PRZYRZĄDAMI

ANALOGOWYM

I. PROTOKÓŁ POMIAROWY

Nieodzowną częścią każdego ćwiczenia laboratoryjnego jest sporządzenie właściwej jego

dokumentacji. Z reguły zbiór podstawowych dokumentów obejmuje wypełniany w trakcie
wykony

wania pomiarów protokół oraz sporządzone na jego podstawie sprawozdanie,

stanowi

ące ostateczne podsumowanie przeprowadzonych pomiarów. Protokół pomiarowy jest

dokumentem, który należy prowadzić na bieżąco z wykorzystaniem wcześniej przygotowanego
for

mularza. Powinien on być zwięzły, ale jednocześnie zawierać taką ilość informacji o

przeprowadzanym eksperymencie i warun

kach w jakich się on odbywał, aby mógł być

zrozumiały przez inne osoby nie biorące bezpośredniego udziału w pomiarach.

Wyniki odczyta

ne z przyrządów powinny być natychmiast notowane. Z uwagi na możliwość

powstania błędów, niedopuszczalne jest jakiekolwiek przeliczanie ich w pamięci przed
wpisaniem do protokołu. Kolejność czynności powinna być następująca: odczyt – zapis –
sprawdzenie od

czytu z zapisem. Niewskazane jest również przepisywanie protokołu, głównie ze

względu na powstające wówczas pomyłki, przeinaczenia, pomijanie tych wyników, które wydają
się mniej ważne lub błędne. Na odrzucenie danego wyniku można decydować się dopiero na
etapie ostatecznego sprawozda

nia, po wykonaniu stosownych obliczeń i rozważeniu wszystkich

warunków wykonania eksperymentu.

Mimo wymogów wypełniania na bieżąco, protokół powinien być prowadzony starannie.

Niechlujne lub nieczytelne notowa

nie wyników jest częstym powodem błędnych interpretacji

i

świadczy o niskiej kulturze technicznej eksperymentatora. Do podstawowych informacji, które

z reguły powinny znaleźć się w każdym protokole należą:
1)

dane dotyczące osoby lub osób przeprowadzających pomiary, miejsce, data i temat,
zestawio

ne najczęściej w formie odpowiedniej tabeli nagłówkowej,

2)

cel pomiarów,

3)

niezbędne dane teoretyczne o przeprowadzanych pomiarach (jeśli wymagane),

4)

wykaz aparatury, najlepiej sporządzony w formie odpowiedniej tabeli,

5) ponumerowane schemat

y układów pomiarowych, umieszczone pod odpowiednimi punktami

pomiarowymi,

6)

wyniki pomiarów sporządzone, o ile to jest tylko możliwe, w postaci tabeli zaopatrzonej
w

numer i tytuł. Tabela jest najbardziej jasną i zwartą formą zapisu. Każda kolumna lub

każdy wiersz w tabeli powinny być oznaczone symbolem wielkości, której wartości one
zawierają, symbolem jednostki, w której te wartości są podawane oraz numerem
porządkowym.

II. ZASADY OPRACOWANIA SPRAWOZDANIA

Sprawozdanie z przeprowadzonych po

miarów tworzy się na podstawie oryginalnego

protokołu pomiarów. W zależności od wymagań stawianych autorowi, może ono przybierać
różne formy. Najczęściej jednak obejmuje następujące części składowe:
1)

tabelę nagłówkową zawierająca dane o autorze, dacie wykonania i tytuł,

2) str

eszczenie będące zwięzłą prezentacją całej treści,

3)

krótki opis podstaw teoretycznych przeprowadzanego doświadczenia (lub doświadczeń
przypisanych do odpo

wiednich punktów pomiarowych protokołu) z uwzględnieniem zwięzłej

prezentacji zastosowanych metod pomiarowych,

4)

opracowane wyniki pomiarów – wyniki wykonanych obliczeń, przykładowe obliczenia,
wykresy,

5)

dyskusję otrzymanych wyników.

2

III. PRZYRZĄDY POMIAROWE

1. Amperomierz analogowy

Przyrząd taki jest najczęściej wykonywany w oparciu o ustrój magnetoelektryczny (ME).

Ustrój taki jest typowym ustrojem amperomierzowym, ponieważ kąt wychylenia organu
ruchomego zależy od natężenia prądu płynącego przez uzwojenie ustroju a nie od napięcia.
Zależność ta jest liniowa. Mierniki ME charakteryzują się dużą czułością i już prądy rzędu



A

czy mA powodują znaczne wychylenie organu ruchomego, do którego mocowana jest
wskazówka miernika.

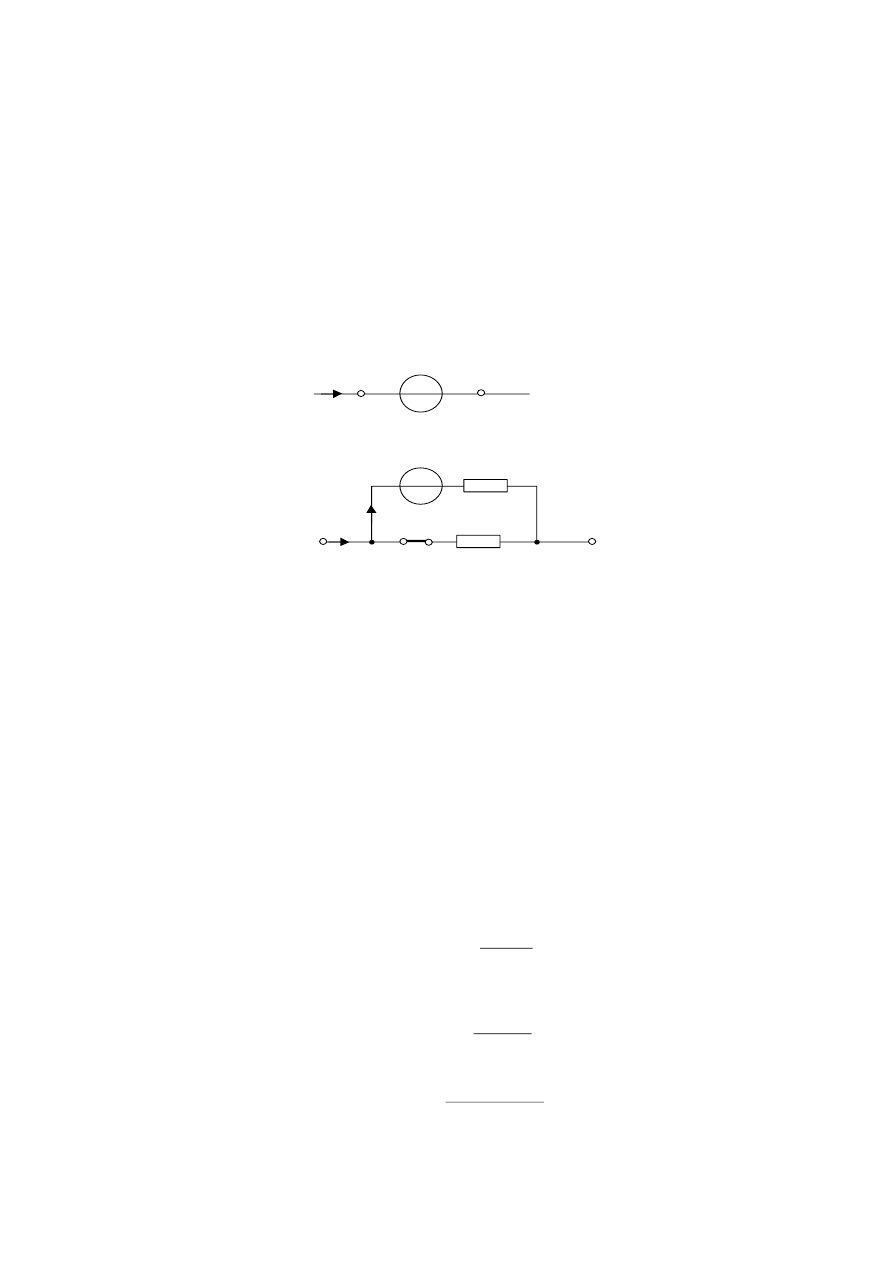
Amperomierze o zakresie pomiarowym od 1



do 25 mA a nawet do 0,5 A wykonywane

są jako amperomierze bezpośrednie, tzn., że przez ustrój miernika płynie cały prąd mierzony
(rys. 1

a). Aby móc zwiększyć zakres natężenia prądu, który można by mierzyć za pomocą

takiego ustroju bocznikuje go rezystorami o wartościach mniejszych od rezystancji ustroju.
Sposób rozszerzania zakresu amperomierza przedstawia rys. 1b.

I

I

N

R

Cu

R

Cu

R

d

R

b

P

a)

b)

I

Cu

Rys.1. Budowa amperomierza ME:

a) amperomierz bezpośredni;
b) amperomierz wielozakresowy z bocznikiem.

Wskazania takiego amperomierza powinny być niezależne od temperatury. Zgodnie z

odpowiednimi przepisami w zakresie temperatur (293



10)K błąd dodatkowy od temperatury

otoczenia nie powinien być większy od błędu podstawowego przyrządu. Rezystory
bocznikujące wykonuje się z manganinu cechującego się niewielkimi zmianami rezystancji przy
nawet znacznych zmia

nach temperatury (niski współczynnik temperaturowy rezystancji).

Tymczasem uzwojenie ustroju ME wykonywane jest z miedzi, która ma współczynnik
temperaturowy rezystancji o dość dużej wartości. Zmiana temperatury spowodowałaby zmianę
rozpływu prądu między ustrojem a bocznikiem. Aby temu zapobiec szeregowo do ustroju ME
umieszcza się rezystor dodatkowy, wykonany z manganinu, który ma kompensować wpływ
zmian temperatury. Można udowodnić, że wartość tego rezystora powinna spełniać następującą
nierówność

d

kl

d

kl

R

R

Cu

d

.

.

4





Stosując odpowiednio prawa Kirchhoffa można wyprowadzić wzór na wartość rezystancji
bocznika R

b

w zależności od prądu nominalnego, na jaki chcemy zaprojektować amperomierz.

Cu

N

Cu

d

Cu

b

I

I

I

R

R

R







)

(

Rezystancja wewnętrzna amperomierza z bocznikiem jest równa

d

Cu

b

d

Cu

b

we

R

R

R

R

R

R

R









)

(

Rezystancja ta musi być jak najmniejsza, aby spadek prądu wywołany włączeniem
amperomierza do obwodu pomiarowego był nie większy niż błąd podstawowy (graniczny)
amperomierza.

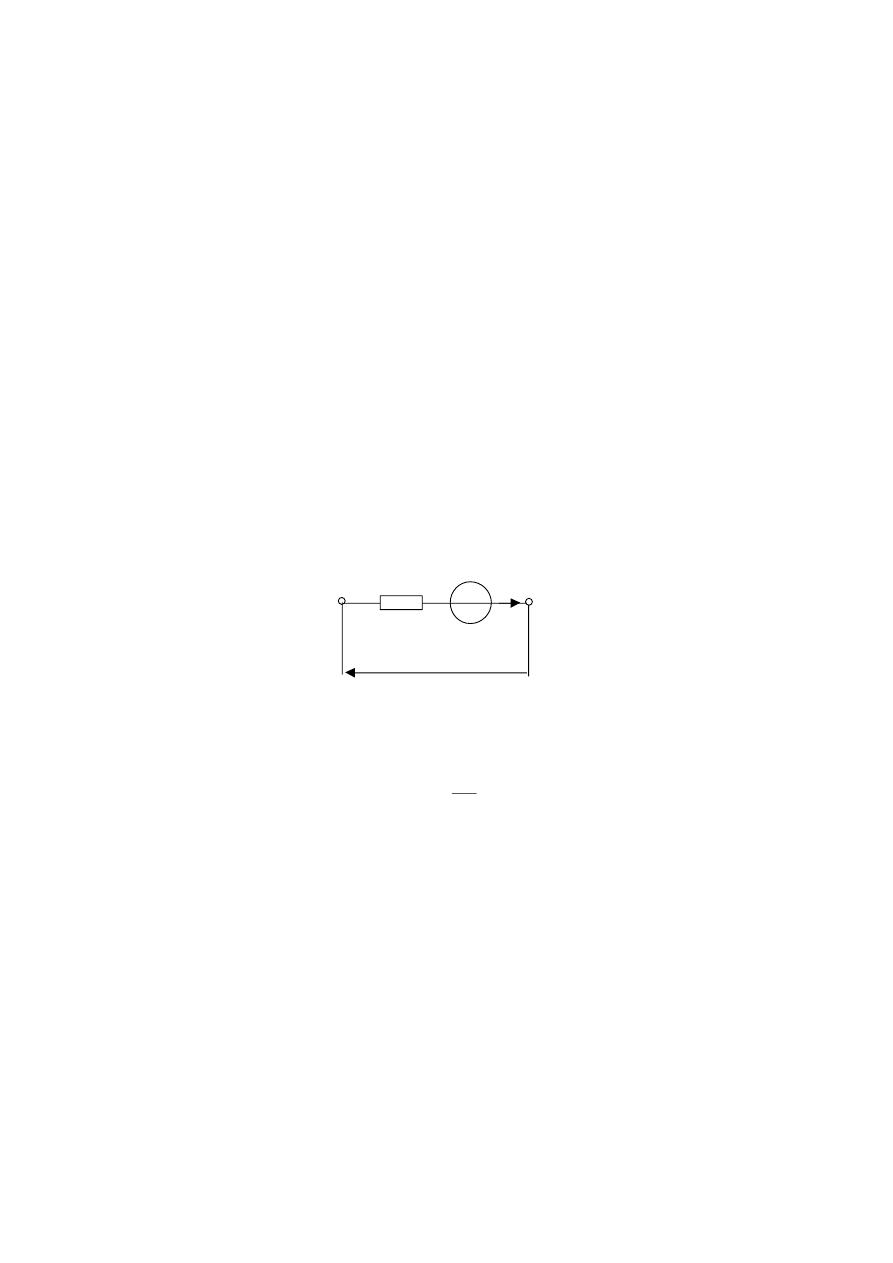
3

2. Woltomierz analogowy

Woltomierze an

alogowe są obecnie wykonywane najczęściej w oparciu o ustrój ME.

Mierniki takie służą do pomiaru napięcia stałego, a jeśli są wyposażone w odpowiedni
przetwornik AC/DC to można je wykorzystywać także do pomiarów napięć zmiennych.
Woltomierz ME powstaje, je

śli szeregowo do ustroju włączy się rezystor R

p

zwany posobnikiem.

Zadaniem takiego rezystora jest zapewnienie dużej rezystancji wewnętrznej woltomierza.
Użycie rezystora o dużej wartości ogranicza wartość natężenia prądu płynącego przez ustrój
ME. Maleje

drastycznie czułość przyrządu, ponieważ ustrój magnetoelektryczny do swojego

działania potrzebuje przepływu prądu.

Niezależnie od zakresu pomiarowego woltomierza, aby wskazówka takiego miernika

mogła wychylać się o ten sam kąt przez ustrój ME musi płynąć ten sam prąd. Zgodnie z
prawem Ohma, aby zapewnić ten warunek zmiana zakresu pomiarowego wymusza zmianę
wartości rezystancji posobnika. Im zakres woltomierza jest mniejszy, tym rezystancja R

p

jest

mniejsza. Maleje także rezystancja wewnętrzna. Rezystancja wewnętrzna typowych
woltomierzy analogowych waha się w przedziale od kilkudziesięciu omów do kilkudziesięciu
kiloomów. Jest to podstawowa wada przyrządów o takiej konstrukcji.

Bardzo często dla woltomierzy analogowych podawana jest tzw. jednostkowa

rezys

tancja wewnętrzna określająca wartość rezystancji wewnętrznej przypadającej na 1 wolt

zakresu pomiarowego. Przeciwdziałanie polega na tym, że cewkę woltomierza nawija się
cieńszym drutem i ma ona więcej zwojów niż amperomierze ME. Zwiększa to czułość
przyr

ządu. Innym sposobem jest zastosowanie na wejściu woltomierza wzmacniacza o dużej

rezystancji wejściowej.

I

N

R

Cu

R

p

U

N

Rys.2. Budowa woltomierza magnetoelektrycznego

Na rys. 2 przedstawiono schemat ideowy typowego woltomierza analogowe

go. Wartości

rezystorów R

p

dobiera się tak, aby spełniona była zależność

N

N

p

I

U

R



Nie uwzględnia ono rezystancji ustroju R

Cu

, ponieważ przyjęto założenie, że R

p



R

Cu

.

Jeżeli zrezygnuje się z posobników, to ustrój ME może być także wykorzystany do pomiaru
napięcia o wartości nominalnej

Cu

N

N

R

I

U



Mała rezystancja wewnętrzna woltomierza może jednak spowodować zakłócenie pracy
badanego urządzenia, ponieważ ulegnie zmianie rozpływ prądów w obwodzie pomiarowym.
Zjawisko to jest

źródłem błędu dodatkowego, którego wartość nie może przekraczać wartości

błędu podstawowego woltomierza.

4

3. Omomierz analogowy

Omomierze analogowe wykonuje się w oparciu o ustrój ME. Służą one do pomiaru

rezystancji liniowej lub do sprawdzania ciągłości obwodu (wykrywanie stanu zwarcia lub
rozwarcia). Idea pracy omomierza polega na tym, że do obwodu pomiarowego włącza się
badany element. Obwód zasilany jest napięciem stałym - na ogół z bateryjki. Doprowadzone
napięcie wymusza przepływ prądu elektrycznego, którego natężenie jest mierzone za pomocą
amperomierza magnetoelektrycznego. Przyrządy tego typu nie są zbyt dokładne a osiąga się
nimi dokładności pomiaru rzędu kilku do kilkunastu procent – w zależności od klasy. Wadą tego
typu przyrządów jest także to, że w trakcie pomiaru zmianie może ulegać napięcie baterii
spowodowane pobieraniem z niej prądu i wzrostem rezystancji wewnętrznej baterii R

0

.

Podziałka miernika jest silnie nieliniowa. W zależności od konfiguracji obwodu pomiarowego
woltomierza i spos

obu włączania rezystora badanego względem amperomierza (ustroju ME)

rozróżnia się omomierze szeregowe i równoległe.

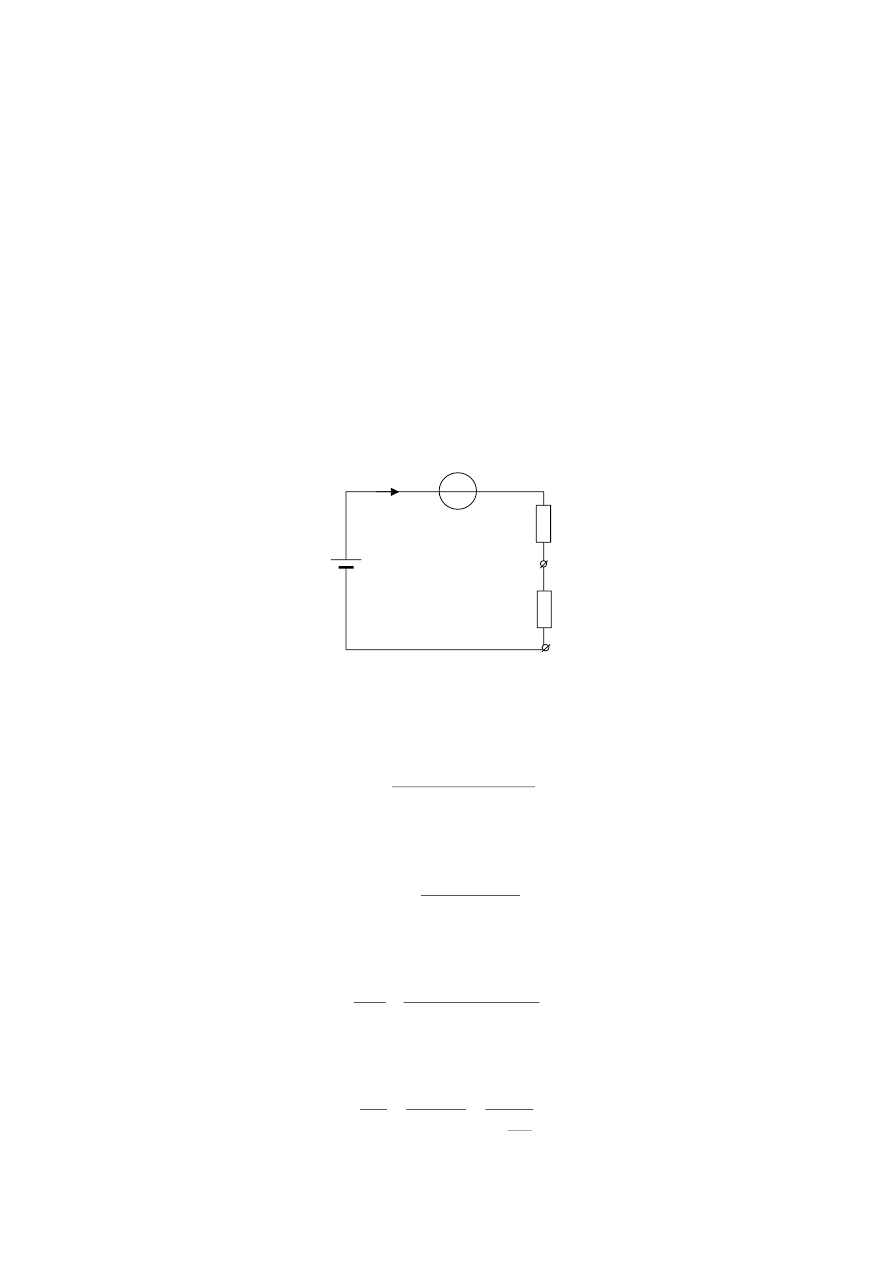
3.1. Omomierz szeregowy

Schemat omomierza szeregowego przedstawia rys. 3

. Układ składa się ze źródła

napięcia stałego o sile elektromotorycznej E i rezystancji R

0

, rezystora R

S

i ustroju

magnetoelektrycznego. Badany element włączany jest szeregowo do pozostałych elementów.

R

s

R

x

E

R

Cu

R

0

I

Rys.3. Schemat omomierza szeregowego

Wartość prądu płynącego przez ustrój ME jest równa

X

S

Cu

x

R

R

R

R

E

I









0

Największy możliwy prąd w układzie jest uzyskiwany wtedy, gdy rezystor R

x

stanowi zwarcie.

S

Cu

R

R

R

E

I







0

max

Dzieląc obydwa równania stronami otrzymamy

X

S

Cu

S

Cu

X

R

R

R

R

R

R

R

I

I













0

0

max

Jeśli uwzględnimy, że R

S

>> (R

0

+ R

Cu

),

to można przyjąć, że R

0

+ R

Cu

+ R

S

= R

we

, a wówczas

we

X

X

we

we

X

R

R

R

R

R

I

I









1

1

max

5

Ponieważ kąt wychylenia organu ruchomego jest równy



= c I , to

we

X

X

R

R





1

1

max





Równanie powyższe opisuje charakterystykę przetwarzania omomierza szeregowego. Zgodnie
z nim mo

żna wyróżnić trzy istotne punkty charkterystyki przetwarzania:

- R

X

= 0

-



X

=



max

;

- R

X

= R

we

-



X

=



max

/2 ;

- R

X

=



-



X

= 0.

Wynika z tego, że podziałka ma nietypowy przebieg – od prawej do lewej i jest silnie nieliniowa.
Przykład podziałki omomierza szeregowego przedstawia poniższy rys. 4.

2

1

4

6

0

10





Rys. 4

. Podziałka omomierza szeregowego

Dla omomierza szeregowego błąd graniczny jest wyrażany następująco:

2

1

100

.



















we

m

we

g

R

R

R

d

kl

R

gdzie: R

we

– wartość rezystancji wewnętrznej omomierza;

R

m

– wartość rezystancji mierzonej (wartość, którą wskazał miernik).

Dokładność pomiaru dla omomierza szeregowego jest określona następująco:

2

%

1

.

















we

m

m

we

R

R

R

R

d

kl

R



Silna nieliniowość podziałki powoduje, że klasę dokładności tego miernika określa się

inaczej niż standardowo. Analizując powyższe wzory dochodzimy do wniosku, że pomiar tym
miernikiem, jest tym dokładniejszy, im wskazówka znajduje się bliżej środka podziałki.

Z drugiej jednak strony, jeśli przyrząd jest zasilany z bateryjki, to im rezystancja mierzona

jest mniejsza, tym większy prąd pobieramy, a to powoduje zwiększenie rezystancji wewnętrznej
baterii, a co za tym idzie maleć będzie SEM baterii.

Wynika z tego, że omomierzem szeregowym powinno się mierzyć rezystancje duże –

powyżej połowy wychylenia. Jednocześnie przed każdym pomiarem powinno się zwierać
zaciski omomierza i korektorem położenia ustawiać położenie wskazówki na „zero”. Przy
dużych wartościach R

x

mniejsza jest też wrażliwość omomierza na zmiany warunków otoczenia.

6

3.2. Omomierz równoległy

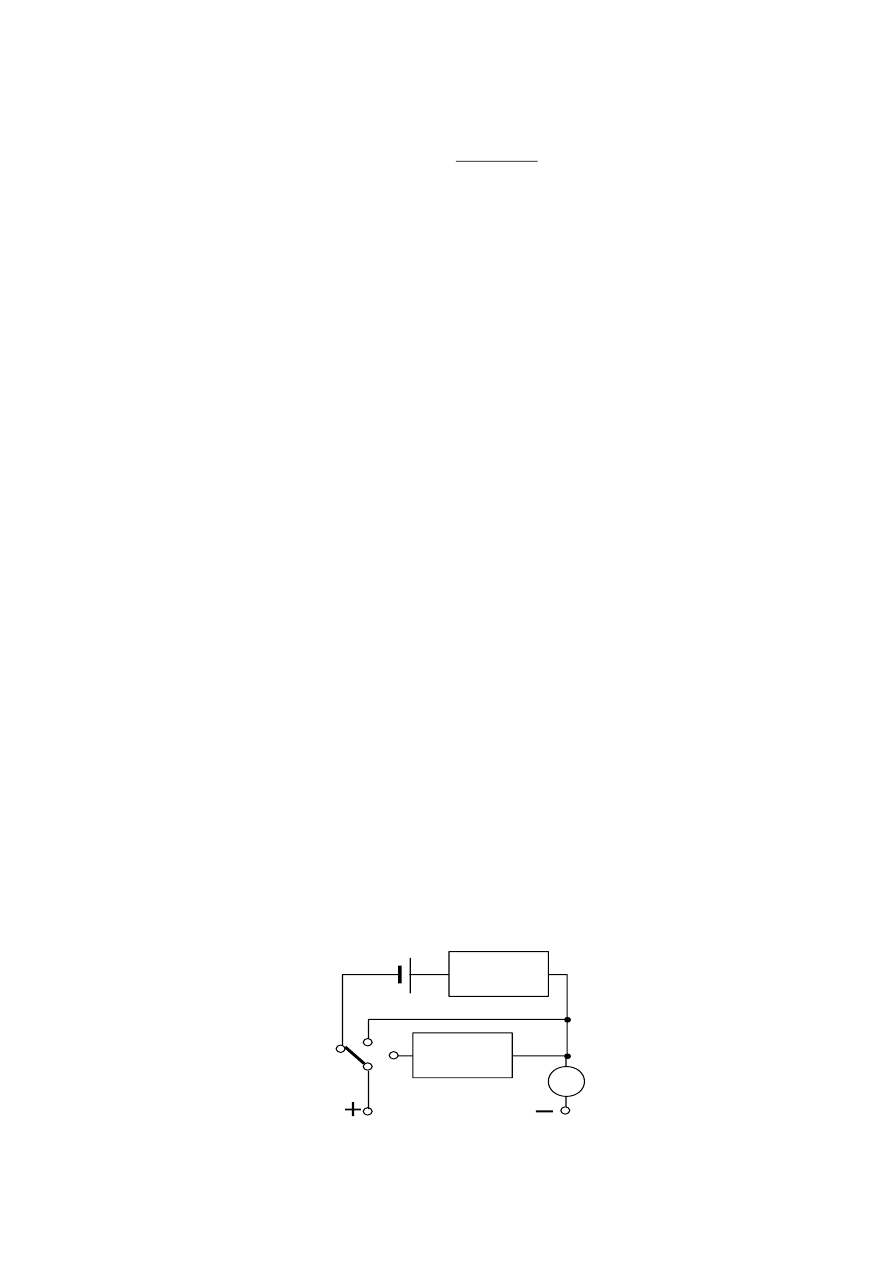
Schemat omomierza równoległego przedstawia rys. 5. Układ pomiarowy składa się z

szeregowo połączonych źródła napięcia stałego o rezystancji wewnętrznej R

0

i sile

elektromotorycznej (SEM) równej E, rezystora dodatkowego R

S

i ustroju ME. Element badany o

rezystancji R

X

włączany jest równolegle do ustroju miernika.

R

s

R

x

E

R

Cu

R

0

I

Rys. 5

. Schemat ideowy omomierza równoległego

Taka konfiguracja układu powoduje, że przez ustrój ME płynie prąd o wartości

X

Cu

S

Cu

Cu

S

R

R

R

R

R

R

R

R

E

I











0

0

Gdy rezystor R

X

stanowi rozwarcie dla obwodu, wartość tego prądu jest największa i wynosi

Cu

S

R

R

R

E

I







0

max

Dzieląc te równania stronami otrzymamy następujący wzór

max

1

1

I

R

C

I

X





gdzie:

S

Cu

S

Cu

R

R

R

R

R

R

C









0

0

)

(

Uwzględniając, że wychylenie organu ruchomego w ustroju ME jest liniową funkcją prądu, to
wyrażenie na równanie charakterystyki przetwarzania omomierza równoległego ma postać

X

R

C





1

max





Współczynnik C ma wymiar rezystancji i czasami jest nazywany rezystancją środka skali.

Podobnie jak w omomierzu szeregowym podziałka jest silnie nieliniowa jednak analiza

powyższego wyrażenia wskazuje na to, że jest to podziałka prosta, która biegnie od lewej do
prawej strony. Przykład takiej podziałki przedstawia rys. 6.

2

1

4

6

0

10





Rys. 6

. Podziałka omomierza równoległego

Dla omomierza równoległego błąd graniczny jest wyrażany następująco:





C

C

R

d

kl

R

m

g

2

100

.









gdzie:

7

C

– stała charakterystyczna dla danej konstrukcji omomierza (w przybliżeniu C = R

we

dla środka

podziałki)

Dokładność pomiaru dla omomierza równoległego jest określona następująco:





C

R

C

R

d

kl

R

m

m

2

%

.









Z wyrażeń powyższych wynika, że dokładność pomiaru omomierzem jest silnie zależna od

wartości mierzonej, a wartość klasy przyrządu umieszczana na podzielni miernika nie ma
bezpośredniego związku z dokładnością pomiaru. Dokładniejsza analiza powyższych wzorów
pozwala na wyciągnięcie następujących spostrzeżeń:
-

pomiar omomierzem szeregowym jest najdokładniejszy przy R

m

= R

we

;

- pomiar omomierzem r

ównoległym jest najdokładniejszy R

m

= C, wtedy



%

R = 4 kl.d.

-

zakres pomiarowy omomierza należy tak dobierać, aby 0,4R

we



R

m



2,5R

we

, wtedy



%

R = 5 kl.d.

W związku z powyższym można stwierdzić, że omomierze analogowe są przyrządami

mało dokładnymi, a ich zakres zastosowań jest ograniczony do pomiaru dużych rezystancji w
przypadku omomierza szeregowego i małych rezystancji w przypadku omomierzy równoległych.

D

okładność pomiaru jest największa w okolicach środka podziałki. Można udowodnić, że

omomierz równoległy jest mniej wrażliwy na zmianę warunków pracy (temperatura, obce pola
zakłócające, itd.) przy małych wartościach rezystancji. Zakres pomiarowy powinno dobierać się
tak, aby wskazówka miernika znajdowała się tuż poniżej środka skali.

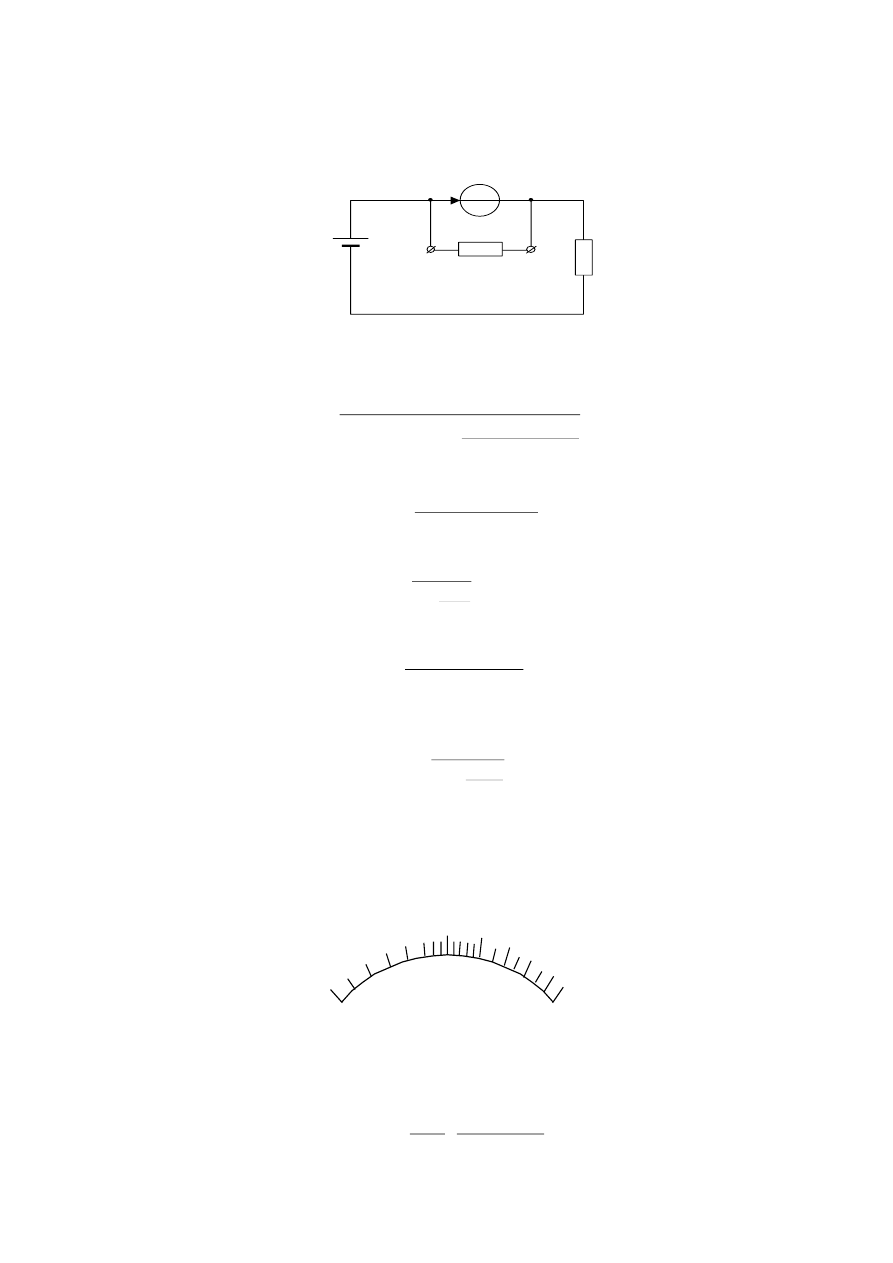
4. Multimetr analogowy

Typowy multimetr analogowy zbudowany jest tak, jak na rys. 7

. Składa się on z

amperomierza ME, zestawu posobników, zestawu rezystorów R

S

i przełącznika funkcyjnego.

Przełącznik funkcyjny pozwala na wybranie funkcji pomiarowej w multimetrze – omomierz (R),
amperomierz (I), woltomierz (U). Podstawową funkcją pomiarową jest pomiar prądu przez
amperomierz ME. Każda inna funkcja pomiarowa jest realizowana przez dodanie do obwodu
amperomierza zestawu rezystorów dodatkowych (R

S

lub posobników) a w przypadku

omomierza dołączenie jeszcze źródła napięcia stałego. Jeśli w układzie zostanie zastosowany
dodatkowo przetwornik AC/DC to przyrząd będzie mógł mierzyć także prąd i napięcie zmienne.

Wadą multimetrów jest to, że wymagają od użytkownika większej ostrożności niż

przyrządy monofunkcyjne, ponieważ oprócz bezpiecznego doboru zakresu pomiarowego należy
uważać, aby nie pomylić funkcji pomiarowej. Wybranie np. funkcji omomierza i włączenie
przyrządu do zasilanego obwodu pomiarowego grozi trwałym uszkodzeniem miernika.

Przed wykonaniem pomiarów wybranej wielkości pamiętać należy, że przed włączeniem

zasilania w obwodzie pomiarowym:
-

zakres pomiarowy miernika należy ustawiać na maksymalny możliwy;

-

korektorem położenia ustawić wskazówkę miernika na „zero”;

- przy

rząd powinien pracować w warunkach dla których został stworzony (pozycja pracy,

temperatura otoczenia, udary, itd.).

Zestaw

posobnik ów

A

Zestaw

rezystorów

R

S

U

I

R

P

E

Rys.7. Schemat blokowy multimetru analogowego

8

5. Pomiar rezystancji z wykorzystaniem amperomierza i woltomierza

Przy braku omomierza, pomiaru rezystancji można dokonać metodą pośrednią, przez

pomiar napięcia i prądu płynącego przez badany rezystor. Wielkości podstawić można do wzoru

X

X

X

I

U

R



Rozróżnia się dwa układy pomiarowe – układ z poprawnie mierzonym prądem oraz układ z

poprawnie mierzonym napięciem. Pod warunkiem, że wyeliminuje się tzw. błąd metody, dla
obydwu układów dokładność pomiaru wynosi

X

X

I

U

R











Gdzie:



U

X

– dokładność pomiaru napięcia woltomierzem;



I

X

– dokładność pomiaru prądu.

Jeśli błędu metody nie wyeliminuje się, to można udowodnić, że układ z poprawnie

mierzonym prądem powinno stosować się do pomiaru dużych rezystancji, tzn. takich, które
spełniają nierówność:

A

V

X

R

R

R



gdzie: R

V

– rezystancja wewnętrzna woltomierza;

R

A

– rezystancja wewnętrzna amperomierza.

Układ z poprawnie mierzonym napięciem jest dokładniejszy, jeśli:

A

V

X

R

R

R



Przyjmuje się jednak, że wykonujący pomiary dobrał właściwie zakresy pomiarowe mierników.
Jeśli w pomiarach wykorzystywane są przyrządy elektroniczne, to na ogół spełniony jest
warunek

R

V

>> R

X

i należy stosować układ z poprawnie mierzonym napięciem.


6

. Układ z poprawnie mierzonym prądem

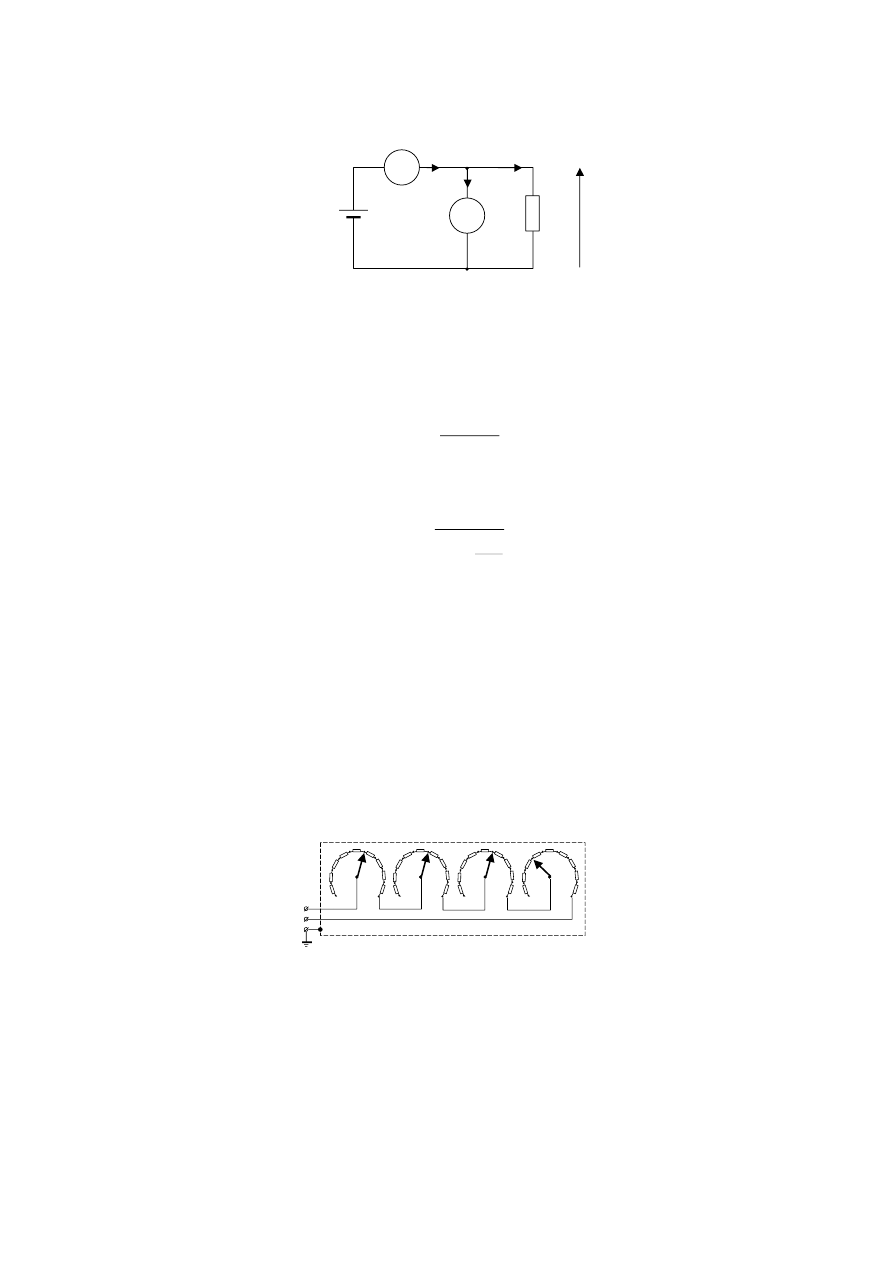
Schemat układu pomiarowego przedstawia rys. 8. W układzie tym, przez amperomierz

płynie ten sam prąd, co przez badany rezystor (stąd nazwa układu).

Natomiast woltomierz wskazuje napięcie nie na rezystorze badanym, lecz na

szeregowym połączeniu rezystora badanego i amperomierza, który charakteryzuje się
rezy

stancją wewnętrzną R

A

. W związku z tym, rzeczywista wartość rezystancji wynosi

X

A

X

XR

I

U

U

R





gdzie U

A

= I

X



R

A

.

Jeśli tak, to

A

X

X

XR

R

I

U

R





Zakłada się, że R

A

jest znane z nieskończoną dokładnością, co nie jest prawdą.

A

V

E

U

R

U

A

U

X

I

X

R

XR

Rys.8

. Schemat układu do pomiaru rezystancji z poprawnie mierzonym prądem

9

7

. Układ z poprawnie mierzonym napięciem

Na rys. 9

przedstawiono schemat układu pomiarowego.

A

V

R

XR

E

I

R

I

V

U

X

I

X

Rys. 9

. Schemat układu do pomiaru rezystancji z poprawnie mierzonym napięciem

W układzie tym poprawnie mierzoną wielkością jest napięcie. Ze względu na to, że

rezystancja wewnętrzna woltomierza R

V

jest skończona, amperomierz wskazuje sumę prądów

I

V

oraz I

R

. W związku z tym można zapisać, że wartość rzeczywista rezystancji mierzonej

wynosi

V

X

X

XR

I

I

U

R





gdzie I

V

= U

X

/ R

V

. Jeśli tak, to

V

X

X

X

XR

R

U

I

U

R





Przyjmuje się założenie, że R

V

jest znane z nieskończoną dokładnością.

7. Rezystor dekadowy

Rezystory dekadowe są regulowanymi wzorcami rezystancji – jako wzorce są

przyrządami pomiarowymi. Rezystory takie składają się z dekad. Każda z dekad składa się z
rezystorów stałych (nieregulowanych) o wartościach tego samego rzędu (np. jedności,
dziesiątki, setki, tysiące omów). Dany rezystor w dekadzie wybierany jest za pomocą
przełącznika. Wartość danej dekady może się zmieniać w zakresie (0



10)



n



, gdzie n

– rząd

dekady. Wszystkie dekady rezystora dekadowego są połączone szeregowo. Sposób połączeń
dekad w rezystorze dekadowym przedstawiono na rys.17.

R

3

R

2

R

1

R

0

Rys.18. Schemat połączeń rezystora dekadowego z ekranem

Do podstawowych parametrów rezystorów dekadowych należ prąd nominalny, liczba

dekad, zakres nominalny, klasa dokładności. Ze względu na specyfikę wykonania takie
parametry jak klasa czy prąd znamionowy określa się dla każdej z dekad osobno.

Klasę dekady określa się względem jej wartości nominalnej. Jeśli więc istnieje potrzeba

wyznaczenia błędu granicznego ustawienia żądanej wartości rezystancji, należy wyznaczyć
błędy graniczne dla każdej z dekad, na której wybrano wartość inną niż zerowa i zsumować je
ze sobą (rezystancja połączenia szeregowego dekad jest równa sumie wartości rezystancji
rezystorów wybranych w poszczególnych dekadach) – zgodnie z prawem przenoszenia błędów.

10

III. POMIARY

1. Odczyt wartości mierzonej na podstawie wskazań przyrządów analogowych

Jednym z podstawowych parametrów przyrządów analogowych (wskazówkowych) jest

stała miernika. Jeżeli miernik jest wyposażony we wskaźnik, który ma naniesioną podziałkę
liniową, to stała miernika jest równa stałej podziałki. Stała podziałki jest to stosunek wartości
nominalnej podzakresu pomiarowego X

N

do maksymalnej liczby działek na podziałce miernika



max

max



N

X

S



W przyrządach o podziałce liniowej odczytu wartości mierzonej dokonuje się mnożąc

liczbę działek



, o którą wychyliła się wskazówka miernika od położenia początkowego przez

stałą podziałki S. Wynik pomiaru będzie więc równy

N

m

X

X

S

X

X

max















Jeżeli miernik ma podziałkę silnie nieliniową (różne odległości między kolejnymi działkami),

to należy określić stałą fragmentu podziałki. Taka sytuacja zachodzi w omomierzach
analogowych. Przyjmuje się założenie, że na podziałce nieliniowej można określić pewne
przedziały, w których jest ona liniowa. Na ogół granice takich przedziałów są opisane działkami
oznaczonymi liczbowo. Wynik pomiaru będzie równy

min

min

'

'

'

X

X

X

S

X

m





















gdzie:



’ – liczba działek, o które odchyliła się wskazówka od początku rozpatrywanego przedziału;







max





min

– szerokość przedziału liniowego w działkach;



X



X

max



X

min

przyrost wartości wielkości mierzonej powodującej zmianę położenia

wskazówki od położenia



min

do



max

.

Wadą przyrządów analogowych jest możliwość niedokładnego odczytu wartości

wska

zywanej przez urządzenie odczytowe miernika. Urządzenie to składa się z podzielni, na

której naniesiona jest podziałka oraz wskazówki – materialnej (rys.10) lub świetlnej (rys.3).
Podziałka jest to uporządkowany zbiór znaków (najczęściej kresek – wskazów). Dla ułatwienia
odczytu niektóre z tych znaków mogą być opisane cyframi. Część podziałki między sąsiednimi
wskazami nazywamy

działką elementarną. Długość podziałki oraz liczba działek są ściśle

zależne od klasy oraz gabarytów miernika. Im klasa wyższa tym podziałka dłuższa, a liczba
działek większa [1].

2

1

Rys.10

. Wskazówka nożowa i skala lustrzana: 1 – lustro, 2 – wskazówka

Charakterystyczną cechą mierników analogowych jest zdolność rozdzielcza, która określa

najmniejszą część działki możliwą do odczytania. W zależności od odległości między
sąsiednimi wskazami, przyjmuje się, że zdolność rozdzielcza wynosi 0.5, 0.2 lub 0.1 mm
(działki). Przyjęcie zbyt małej zdolności rozdzielczej zwiększa błąd odczytu.

Błąd odczytu ma charakter błędu przypadkowego i jest zależny przede wszystkim od

staranności eksperymentatora. Przy pomiarach jednokrotnych błąd taki jest trudny lub wręcz
niemożliwy do oszacowania. Błąd odczytu może zostać także popełniony, jeśli wykonujący

11

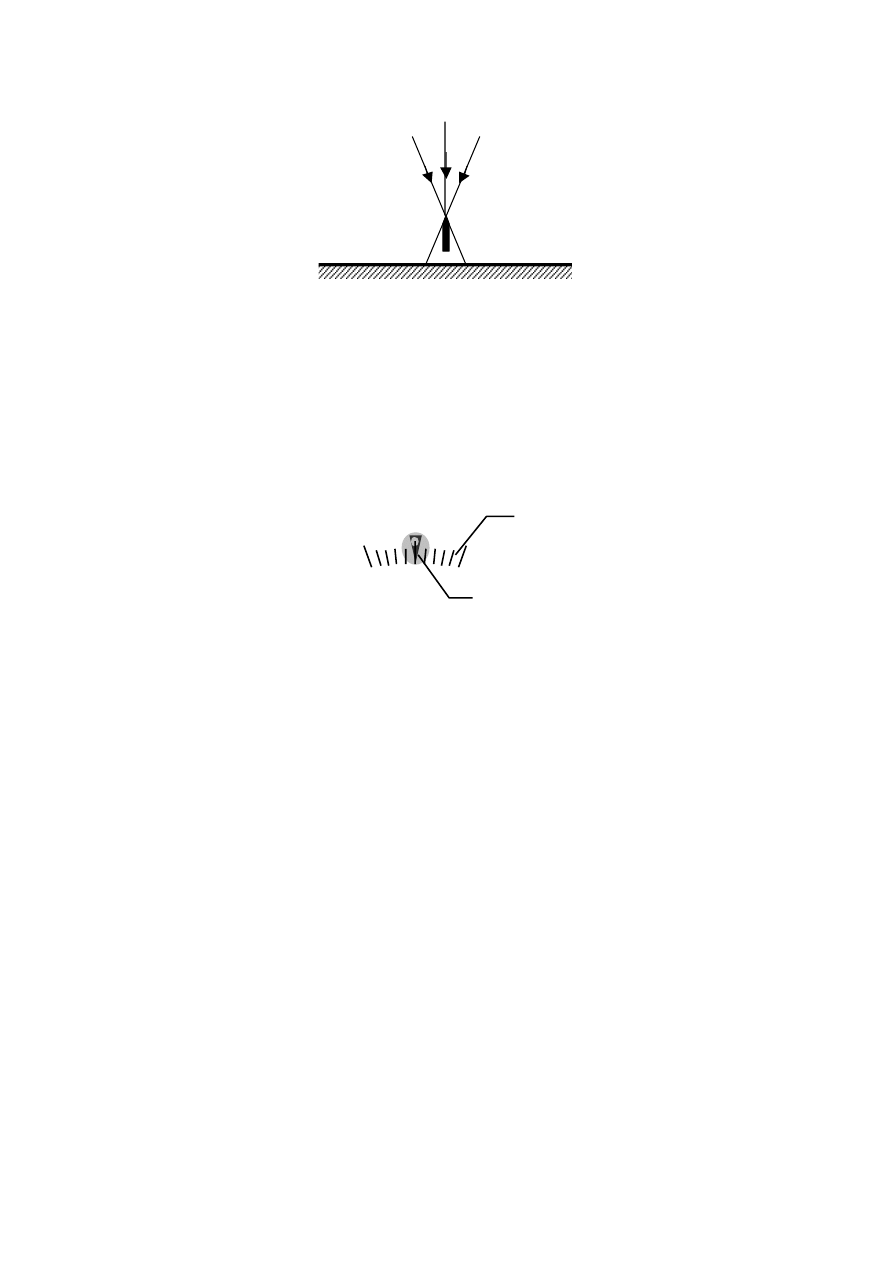
pomiary nie patrzy na

wskazówkę prostopadle do płaszczyzny podzielni. Jest to błąd krzywego

patrzenia, nazywany także błędem paralaksy. Istotę tego błędu przedstawia rys. 11.

źl

e

źle

d

o

b

rz

e

k oniec
wskazówki

Rys.11

. Sposób powstawania błędu paralaksy.

Błąd paralaksy można wyeliminować patrząc na wskazówkę prostopadle do podzielni.

Ułatwia to umieszczone pod wskazówką lusterko lub stosowanie wskazówki świetlnej.
Wskazówka świetlna powstaje na zasadzie odbicia światła z żarówki od lustereczka, na
którym jest naniesiony znacznik wskazówki. Lustereczko jest przymocowane do osi, której kąt
odchylenia od położenia równowagi zależy od wartości wielkości mierzonej.

Przemieszczająca się wzdłuż podziałki plamka uniemożliwia powstanie błędu paralaksy,

ponieważ cień wskazówki znajduje się bezpośrednio na podzielni.

2

1

Rys.12

. Skala i wskazówka świetlna: 1 – podziałka,

2

– plamka świetlna ze znacznikiem wskazówki

3. Błąd graniczny i dokładność pomiaru przy pomiarach jednokrotnych

Wskazanie przyrządu bez podania granic błędu, z jakim pomiar został wykonany, ze

względów poznawczych nie ma żadnego znaczenia. Można nawet stwierdzić, że pojęcia pomiar
i błąd pomiaru lub jego dokładność są pojęciami nierozerwalnymi. Wynik pomiaru X

r

powinien

być zawsze przedstawiany w postaci

X

X

X

g

m

r







gdzie:
X

m

– wartość zmierzona zapisana z uwzględnieniem odpowiedniej liczby miejsc znaczących;



g

X

– błąd graniczny pomiaru.

Ze względu na wymaganą dokładność, pomiary można podzielić na:

- laboratoryjne wysokiej precyzji (



%

X < 0,05%);

-

laboratoryjne średniej dokładności

(0,05%





%

X



0,5%);

- techniczne

(



%

X > 0,5%).

W zależności od tego do rachunku błędów podchodzi się z różną precyzją.
Poniżej omówiono metodykę wyznaczania błędów przy pomiarach technicznych. Pomiar

danej wielkości odbywa się na ogół jednokrotnie a błąd ma na ogół charakter systematyczny
ograniczony dokładnością użytych przyrządów (jego błędem podstawowym i błędami
dodatkowymi. Ogólnie można spotkać dwa przypadki:

– pomiar bezpośredni (wartość wielkości mierzonej jest określana na podstawie wskazania

jednego przyrządu);

-

pomiar pośredni (wyznaczana wielkość jest funkcją kilku wielkości mierzonych

bezpośrednio).

12

3.1. Pomiary bezpośrednie
3.1.1. Błąd graniczny pomiaru przyrządów analogowych

Jeśli klasa przyrządu pomiarowego jest oznaczana symbolem kl.d np. 1,5 (co oznacza

1,5%), to błąd graniczny pomiaru wielkości X wyznaczany jest za pomocą wyrażenia

N

g

X

d

kl

X

%

100

.





gdzie:
X

N

– wartość nominalna (maksymalna) zakresu pomiarowego (dla przyrządów

wielozakresowych jest to wartość maksymalna podzakresu pomiarowego, na którym był
wykonywany pomiar).
Istotne jest to, że wartość błędu granicznego pomiaru jest stała na danym podzakresie

miernika i nie zależy od wartości wielkości mierzonej X

m

.

Jeśli dokładność przyrządu pomiarowego jest wyrażana w procentach wartości mierzonej,

co jest oznaczane na podzielni miernika wychyłowego, jako kl.d, np. 1,5, to przy wyznaczaniu
błędu granicznego pomiaru korzysta się z zależności

m

g

X

d

kl

X

%

100

.





gdzie:
X

m

– wartość mierzona badanej wielkości (wartość, którą wskazał miernik).

Wartość błędu granicznego jest w tym przypadku zależna od wartości wielkości mierzonej i

nie jest stała na danym podzakresie miernika.

W niektórych analogowych elektronicznych przyrządach pomiarowych można spotkać się

z wyrażeniem opisującym zależność błędu granicznego pomiaru danym przyrządem zarówno
od wartości mierzonej X

m

,

jak i od wartości nominalnej zakresu pomiarowego X

N

.

Wyrażenie to jest na ogół podawane w postaci:





N

m

g

X

b

X

a

X

%

%









gdzie:
a, b

– stałe charakterystyczne dla danego przyrządu.

Taki sposób opisu właściwości dokładnościowych miernika jest stosowany wtedy, gdy

odpowiednią zależność udało się wykryć w procesie produkcyjnym przyrządu.

Warto zauważyć, że w granicznym przypadku, jeśli X

m

= X

N ,

to



g

X =



(a

%

+ b

%

) X

N

.

Przez analogię z wyrażeniem (5) można zapisać kl.d = a

%

+ b

%

.

Czasami składowa błędu b

%

X

N

jest podawana jawnie w jednostkach wielkości mierzonej.

3.1.3. Dokładność pomiaru

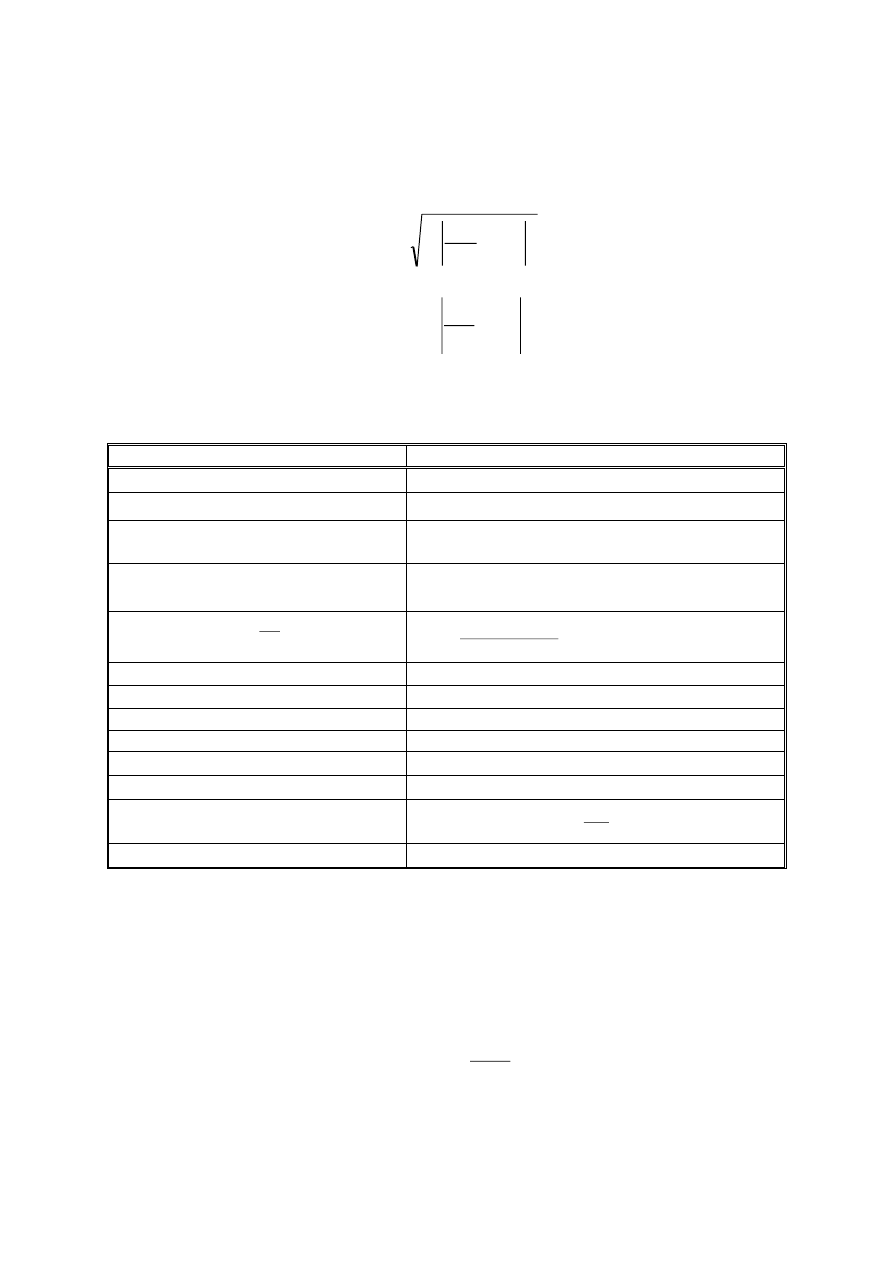
Dokładnością pomiaru nazywa się stosunek błędu granicznego do wartości mierzonej

%

100

%

m

g

X

X

X







Jak widać dokładność pomiaru może się znacznie różnić od dokładności przyrządu
pomiarowego.

Jeśli błąd graniczny wyrażony będzie równaniem (5) to dokładność pomiaru jest

równa:

d

kl

X

X

X

m

N

.

%





Zgodnie z powyższym równaniem dokładność pomiaru jest nie lepsza od klasy

dokładności przyrządu pomiarowego i jest tym mniejsza im wskazanie przyrządu jest mniejsze.
Nasuwa się więc wniosek, że ze względu na dokładność pomiaru zakres pomiarowy należy
dobierać tak aby zapewnić możliwie największe wychylenie wskazówki miernika.

W

miernikach z klasą wyrażoną jako procent wartości mierzonej dokładność pomiaru jest

równa dokładności przyrządu w całym zakresie wskazań.



%

R = kl.d

13

3.2. Pomiary pośrednie

Przy pomiarach pośrednich zakłada się, że funkcja opisująca wielkość mierzoną ma

postać

)

,....,

(

1

n

X

X

f

Y



Graniczny b

łąd pomiaru określony jest zależnością:















n

i

i

g

i

g

X

X

Y

Y

1

2

lub w postaci uproszczonej (błąd najgorszego przypadku) jako:















n

i

i

g

i

g

X

X

Y

Y

1

gdzie:



g

X

i

– błąd graniczny i-tej wielkość mierzonej bezpośrednio określony tak jak w przypadku

pomiarów bezpośrednich. Wyrażenia te określają tzw. prawo przenoszenia błędów.

Tabela 1

Propagacja błędów

Zależność funkcyjna

Sposób propagacji błędu

2

1

X

X

Y





2

1

X

X

Y











2

1

X

X

Y



2

1

1

2

X

X

X

X

Y













Y =



X

1

+



X

2







n

i

i

i

X

a

Y

1

 







n

i

i

i

X

a

Y

1







n

i

a

i

i

X

Y

1







n

i

i

i

X

a

Y

1





2

1

X

X

Y



2

2

2

1

1

2

X

X

X

X

X

Y













Y =



X

1

+



X

2

aX

Y



, X

m



0

X

a

Y









Y =



X

a

X

Y



, X

m



0

X

aX

Y

a









1



Y = a



X

X

Y

sin



X

Y







cos

X

Y

cos



X

Y







sin

tgX

Y



X

X

Y

2

cos

/







ctgX

Y



X

X

Y

2

sin

/







X

Y

ln



, X

m

> 0

X

X

X

Y











X

e

Y



, Y

śr



0

X

e

Y

X









Y =



X

Powyżej przedstawiono tabelę, w której zawarto sposób przenoszenia się błędów dla
wybranych zależności funkcyjnych.

Przy pomiarze pośrednim wynik pomiaru zapisujemy w postaci:

Y

Y

Y

g

m

r







a dokładność pomiaru jest równa:

%

100

%

m

g

Y

Y

Y







Czasami, chcąc wyznaczyć błąd graniczny łatwiej jest wyznaczyć błąd względny pomiaru

(dokładność).

14

4. Dokładność zapisu wyniku i jego błędu

Jednym z podstawowych warunków sporządzenia „dobrego” sprawozdania jest prawidłowy

zapis wyników pomiarów i obliczeń. O sposobie zapisu wyników decydują następująca zasady:
1. Wartość liczbowa uzyskana z pomiaru powinna mieć taką liczbę cyfr znaczących, aby tylko

ostatnia lub przedostatnia były niepewne (zmieniały się w trakcie pomiaru).

2. Przy dodawaniu i odejmowaniu uwzględniamy tylko te cyfry znaczące, które występują we

wszystkich składnikach.

3. W celu dokonania właściwego zaokrąglenia wyniku, działania matematyczne przeprowadza

się z uwzględnieniem najwyżej jednej cyfry znaczącej więcej niż w końcowym wyniku
obliczeń.

4. Zaokrąglenia wyniku dokonujemy w ten sposób, że jeżeli następna cyfra po cyfrze najmniej

znaczącej jest mniejsza od 5, to najmniejszą cyfrę znaczącą pozostawiamy bez zmian, a
jeżeli większa to najmniejszą cyfrę znaczącą zwiększamy o 1. Jeżeli następna cyfra po
najmniejszej cyfrze znaczącej jest równa 5, to wynik zwiększamy o jeden na najmniej
znaczącej cyfrze, jeżeli jest ona nie parzysta a zmniejszamy, jeżeli jest ona parzysta.
Przykład:

16,822



16,82

168,88



168,9

162,15



162,2

162,25



162,2

Warto w tym miejscu zwrócić uwagę na fakt, że zaokrąglając liczby np. 121,5 oraz 122,5 do

liczb całkowitych otrzymamy ten sam wynik 122. W związku ze specyficzną rolą cyfry 5 w
zaokrąglaniu wyników dobrze jest także wiedzieć, jaka cyfra występuje po niej, ponieważ
liczbę 122,51 można już zaokrąglić do liczby 123, a nie do 122.

5. B

łąd jest miarą niewiarygodności ostatniej cyfry znaczącej wartości liczbowej (lub dwóch

ostatnich cyfr), nie zapisuje się go z większą dokładnością niż za pomocą jednej cyfry
znaczącej. Błąd można zapisać z dokładnością do dwóch cyfr znaczących tylko w
następujących sytuacjach:



przy bardzo dokładnych pomiarach;



jeśli ma być użyty do dalszych obliczeń;



jeśli pierwszą cyfrą znaczącą jest 1 (lub 2). W tabeli 2 podano odpowiednie przykłady z
wyjaśnieniami.

Tabela 2

Wynik z błędem

nie zao

krąglonym

Wynik z błędem

zaokrąglonym

Wyjaśnienia

12113



31

12110



30

Zapis typowy. Zaokrąglenie błędu
spowodowało zmniejszenie cyfr znaczących
w wyniku.

122132567



31,6

122132567



32

Dokładny pomiar lub konieczność
wykorzystania do dalszych obliczeń.

121



1,3

121,0



1,3

Po usunięciu cyfry 3 pozostałaby cyfra 1.

122,33



0,26

122,3



0,3

Zaokrąglenie wartości błędu powoduje
zmniejszenie dokładności zapisu wyniku.

122,33



0,002

122,330



0,002

Mała wartość błędu powoduje wzrost
dokładności zapisu wyniku.

15

OPRACOWANIE I PREZENTACJA WYNIKÓW POMIARÓW

Opracowanie danych pomiarowych ma na celu wstępne przygotowanie danych do analizy

i

prezentacji. Mogą to być proste działania, takie jak: zaokrąglanie liczb, sortowanie danych,

normalizacja, odr

zucanie anomalnych wyników, łączenie dwóch lub większej liczby

niezależnych pomiarów pojedynczej wielkości fizycznej.

Bardziej zaawansowana obróbka może polegać na wyznaczaniu zależności funkcyjnej

pomiędzy mierzonymi wielkościami, uśrednianiu danych pomiarowych, kompresji danych.
Zobrazowanie danych pomiarowych w formie graficznej ułatwia ich percepcję przez człowieka.
Zobrazowanie przybiera postać różnorodnych wykresów dwu- i trójwymiarowych, wykonanych
często z użyciem kolorów. W trakcie prezentacji publicznych stosowana jest też animacja,
polegająca na dynamicznym generowaniu wykresów na ekranie.
Obróbka i zobrazowanie danych pomiarowych mogą być obecnie realizowane za pomocą
wygodnych narzędzi komputerowych o bardzo dużych możliwościach obliczeniowych
i

graficznych. Złożone algorytmy numeryczne stają się dostępne i łatwe w użyciu, nawet bez

dogłębnej znajomości aparatu matematycznego. Najczęściej do obróbki danych pomiarowych
używa się popularnego w wielu środowiskach akademickich na świecie, programu Matlab firmy
The MathWorks.

1. Podstawowe zasady przedstawiania wyników pomiarów

Jako regułę podawania wyników pomiarów zaleca się stosowanie konwencji ustalającej

związek pomiędzy niedokładnością pomiaru a formą zapisu jego wyniku, uwzględniającą liczbę
cyfr znaczących.
Cyframi znaczącymi przyjęto nazywać wszystkie cyfry liczby, poczynając od pierwszej cyfry
niezerowej znajdującej się na pozycji najwyższego rzędu dziesiętnego.

Liczba 0.00307 ma trzy cyfry znaczące: 3, 0 i 7;
liczba 0.003070 ma cztery cyf

ry znaczące: 3, 0, 7 i 0.

Zaleca się zapisywać liczby w postaci wykładniczej, w której mantysa zawiera tylko cyfry
znaczące.

Tak więc liczbę 0.00307 należy zapisać jako 3.07 * 10-³,
liczbę 0.003070 zaś jako 3.070 * 10-³ .

Ostatnia cyfra znacząca w każdym wyniku powinna być tego samego rzędu (stać na tym
samym miejscu dziesiętnym) co błąd pomiaru.

Na przykład wynik pomiaru 8.135 V z czterema cyframi znaczącymi wskazuje, że

dokładność pomiaru jest rzędu mV. Jeżeli pomiar był wykonywany z dokładnością 10 mV, wynik
powinien być podany w postaci 8.14 V, to znaczy powinien mieć tylko trzy cyfry znaczące.

Zaokrąglanie liczb.
Często zdarza się tak, że liczbę będącą wynikiem działań na liczbach przybliżonych należy
zaokrąglić. Należy stosować obowiązujące reguły zaokrąglania liczb:

• Jeżeli pierwsza z odrzuconych cyfr jest mniejsza niż 5, to liczba zaokrąglona pozostaje bez

zmian.

• Jeżeli pierwsza z odrzuconych cyfr jest większa niż 5, to do ostatniej cyfry liczby

zaokrąglonej dodaje się 1.

• Jeżeli pierwsza z odrzuconych cyfr równa się 5 i między pozostałymi odrzuconymi cyframi

znajdują się cyfry niezerowe, to do ostatniej cyfry liczby zaokrąglonej dodaje się 1.

• Jeżeli pierwsza z odrzuconych cyfr równa się 5 i wszystkie pozostałe odrzucone cyfry są

zerami,

to ostatnia cyfra liczby zaokrąglonej:

- pozostaje bez zmian, gdy jest parzysta;
-

zostaje zwiększona o 1, gdy jest nieparzysta.

Powyższe zasady można wyjaśnić w następujący sposób:
a). Jeżeli pierwsza z odrzucanych cyfr jest większa niż 5, to ostatnią pozostającą cyfrę liczby

należy zwiększyć o jeden np. zaokrąglając liczbę 1,357 do trzech cyfr znaczących należy

16

napisać 1,36, zaś do dwu cyfr znaczących 1,4 – analogicznie z liczbą 3468, zaokrąglając
do trzech cyfr znaczących należy napisać 3,47*10

3

, czyli 3470

b). Jeżeli pierwsza z odrzucanych cyfr jest mniejsza niż 5, to ostatnią pozostającą cyfrę

zachowuje się bez zmiany np. 3,531 zaokrąglając do trzech cyfr znaczących należy
napisać 3,53 – analogicznie 9642 – 9,64*10

3

, czyli 9640.

c). Jeżeli jedyną odrzucaną cyfrą jest 5, to ostatnią pozostającą cyfrę, liczby w przypadku gdy

jest ona parzysta, zachowuje się bez zmiany, zaś gdy jest nieparzysta, zwiększa się o
jeden np. zaokrąglając liczbę 9,225 do trzech cyfr znaczących należy napisać 9,22 –
analogicznie 2,235

– 2,24.

Dodawanie i odejmowanie liczb przybliżonych.
Wyniki dodawania lub odejmowania liczb o różnej dokładności należy zapisywać z taką
dokładnością, jaką ma liczba najmniej dokładna.
Np. w rezultacie sumowania liczb 45,21 + 0,5312 + 4,721 otrzymamy 50,4622.
Ponieważ pierwszy składnik sumy 45,21 jest najmniej dokładny, wynik sumowania należy
zaokrąglić do tego samego rzędu, czyli do dwóch miejsc po przecinku.
Zatem należy zapisać 45,21 + 0,5312 + 4,721 = 50,46

Mnożenie i dzielenie liczb przybliżonych.
Jeśli dokonuje się mnożenie (lub dzielenie) liczby zawierającej m cyfr znaczących przez liczbę
zawierającą n cyfr znaczących, to iloczyn (iloraz) należy zaokrąglić, aby zawierał m cyfr
znaczących gdy m < n, albo n cyfr znaczących gdy n < m.

Np.

w rezultacie mnożenia liczb 3,235 przez 2,3 otrzymamy 7,4405.

Ponieważ mnożna zawiera cztery, a mnożnik dwie cyfry znaczące, to iloczyn powinien zawierać
dwie cyfry znaczące, a zatem należy napisać, że 3,235 * 2,3 = 7,4

Sposób zapisywania wyników pomiarów i obliczeń
Po dokonaniu oceny błędu, niezależnie od tego czy jest to maksymalny błąd przypadkowy
pojedynczego pomiaru, średni błąd średniej arytmetycznej, zawsze należy zaokrąglić
uzyskany wynik do jednej, a co najwyżej dwu cyfr znaczących.
Wynik pomiar

ów lub obliczeń należy tak zaokrąglić, aby rząd jego ostatniej cyfry

znaczącej był taki sam, jak rząd ostatniej cyfry znaczącej oszacowanego błędu.

Np. Po dokonaniu pomiarów czasu t przebiegu pewnego zjawiska obliczono średni czas t

śr

=

18,413 s i średni błąd wartości średniej s = 0,0478 s.
Wynik obliczeń po zaokrągleniach należy zapisać jako:

t = (18,41 ± 0,05) [s].

Zasady postępowania matematycznego przy opracowywaniu wyników pomiarów

Przy opracowywaniu wyników pomiarów obowiązują następujące zasady postępowania:

a) Obliczenia powinny być przeprowadzane na danych (wynikach pomiarów) podawanych z ich

największą dokładnością.

b) Wszystkie obliczenia przeprowadzane na danych: mnożenie, dzielenie, potęgowanie itd.

należy wykonywać do co najmniej dwóch cyfr znaczących więcej niż zawierały pierwotne
dane. Nie należy wykonywać zaokrągleń, dopóki nie uzyska się ostatecznego wyniku
obliczeń.

c) Przy mnożeniu i dzieleniu wynik należy podawać z taką samą liczbą cyfr znaczących, jaką

zawiera wynik pomiaru o najmnie

jszej liczbie cyfr znaczących wzięty do obliczeń.

Można zaobserwować tendencję do łamania zasady (c) przy stosowaniu do obliczeń
kalkulatora. Rozważmy przykład niewłaściwego użycia kalkulatora do określenia rezystancji na
podstawie cyfrowych pomiarów napięcia i prądu:

17









k

mA

V

I

U

R

493562232

,

3

33

,

2

14

,

8

W przykładzie tym podano wynik obliczenia rezystancji zawierający 10 cyfr znaczących (to
znaczy z dokładnością do μΩ !), podczas gdy wielkości pośrednie mają tylko trzy cyfry
znaczące. Jedynym rozsądnym sposobem jest użycie w odpowiedzi tej samej liczby cyfr
znaczących jaka występuje w wynikach pomiarów pośrednich. Zatem obliczenia należy
przedstawić następująco:









k

mA

V

I

U

R

49

,

3

33

,

2

14

,

8

Rezystancja została podana z taką samą precyzją, z jaką zmierzono napięcie i prąd.

Dokładność przyrządów analogowych dana jest w zasadzie jedną liczbą – klasą

dokładności. Stanowi ona podstawę i jednocześnie punkt wyjścia do obliczania błędu pomiaru
wykonanego tym przyrz

ądem. Częstym zjawiskiem jest bezkrytyczne przyjmowanie za błąd

pom

iaru klasy dokładności przyrządu bez względu na wskazywaną przezeń wartość. Ta

ostatnia ma ogromny wpływ na ostateczny błąd pomiaru dokonanego miernikiem
wskazówkowym.

Błędy pomiarów wykonywanych przyrządami wskazówkowymi
Błąd jakim obarczony jest wynik pomiaru dokonanego pojedynczym przyrządem
wskazówkowym, zawiera kilka składników:

1. Błąd podstawowy wskazań
2. Błąd dodatkowy wskazań
3. Błąd odczytu

Błąd podstawowy
Błąd podstawowy wskazań przyrządu wynika z niedokładności wykonania jego elementów
składowych w procesie wytwórczym. Niedokładności te mają charakter przypadkowy, stąd
błędy wskazań noszą ten sam charakter. Mają one różne wartości dla poszczególnych punktów
podziałki i dla różnych egzemplarzy przyrządów danej serii. Określenie tych indywidualnych
błędów byłoby zbyt kosztowne, dlatego wytwórca określa dla całej serii wyprodukowanych
przyrz

ądów największy możliwy błąd wskazań, którego z wysokim prawdopodobieństwem

(mówi się także – poziomem ufności, wynosi ono P = 0,9973) nie przekroczy błędu wskazań
żadnego egzemplarza w żadnym punkcie podziałki.
Ten najwi

ększy błąd bezwzględny oznaczymy

∆

max

=

3



Jest to tak zwany

błąd trzysigmowy wskazań. Wytwórca odnosi następnie ten błąd do zakresu

pomiarowego przyrz

ądu Zp, otrzymując względny maksymalny błąd wskazań:

%

100

max

max







p

Z



Na koniec nadaje całej serii wyprodukowanych przyrządów wspólną klasę dokładności k
wybieraj

ąc spośród ośmiu znormalizowanych wartości:

0,05%

0,1%

0,2%

0,5%

1%

1,5%

2,5%

5%,

n a j m n i e j s z

ą, która spełnia nierówność:

k



max



U

żytkownik natomiast, nie znając szczegółów procesu określania klasy dokładności (nie znając

rzeczywistej warto

ści błędu

max



, posługuje się „znormalizowaną” jego wartością, czyli klasą

dokładności:

k

%

100

max







p

Z

18

Klasa dokładności określona powyższą zależnością jest tylko pewnym wskaźnikiem

dokładności przyrządu wskazówkowego. Jest to błąd wskazań, z którym mierzona jest wartość
wielko

ści mierzalnej w szczególnym przypadku, mianowicie gdy wskazówka przyrządu odchyla

si

ę do końca zakresu pomiarowego.

We wszystkich pozostałych przypadkach mierzący powinien postępować według podanych

ni

żej zasad:

1). Posługując się definicją klasy dokładności, należy obliczyć w pierwszym kroku błąd

max



.

Znaj

ąc klasę dokładności k i używany podczas pomiaru zakres pomiarowy Zp, oblicza się

ten błąd z poniższego wzoru:

%

100

max

k

Z

p







2) Odnosi si

ę następnie ten błąd do wartości W wskazywanej właśnie przez przyrząd, i oblicza

wzgl

ędny błąd wskazań:

%

100

max







W

w



Podstawiaj

ąc w powyższym wyrażeniu w miejsce

∆

max

wyra

żenie

%

100

max

k

Z

p







,

otrzymamy po

przekształceniach praktyczny wzór na obliczanie względnego błędu wskazań

przyrz

ądu wskazówkowego:

W

Z

k

p

w





gdzie:

w



- wzgl

ędny błąd wskazań przyrządu

k -

klasa dokładności przyrządu

Zp - zakres pomiarowy

tego przyrządu

W - wskazanie przyrz

ądu w chwili pomiaru (0



W



Zp)

Z

powyższego wyrażenia widać, że przy zmniejszaniu się wskazania W do zera, błąd

w



d

ąży do nieskończoności.

Wynika st

ąd ważne zalecenie, by pomiary przeprowadzać przy możliwie jak największym

odchyleniu

wskazówki przyrządu, co osiąga się przez wybór odpowiedniego zakresu

pomiarowego przyrz

ądu jak najbardziej zbliżonego do wartości wielkości mierzonej.

Błąd dodatkowy
Błąd ten związany jest z przekroczeniem podczas pomiaru znamionowych warunków pracy
przyrz

ądu. Znamionowe warunki określone są przez następujące parametry.

1. Temperatur

ę otoczenia (np. + 10 °C ¸ +30 °C)

2. Wilgotno

ść powietrza (np. do 85%)

3. Nat

ężenie obcych pól magnetycznych (np. do 5 Oe)

4. Cz

ęstotliwość znamionową (np. 50 Hz) lub przedział dopuszczalnych częstotliwości (np.

20-50-400 Hz)

5. Współczynnik zawartości harmonicznych, charakteryzujący stopień odkształcenia od

sinusoidy krzywej napi

ęcia lub prądu (np. h



5%)

6. Sposób położenia przyrządu podczas pracy (np. pionowe albo poziome, albo pod

okre

ślonym kątem, np. 30°)

Powy

ższe warunki podane są bądź bezpośrednio na przyrządzie, bądź w dołączonej metryce. Z

reguły błąd ten jest pomijany, zakłada się bowiem, że przyrząd analogowy będzie
eksploatowany w warunkach normalnych.

19

Błąd odczytu
Błąd ten wynika z niedokładnego oszacowania przez mierzącego położenia wskazówki
przyrz

ądu między dwiema sąsiednimi kreskami działowymi podziałki. Gdyby podczas pomiaru

wskazówka spoczęła dokładnie na kresce działowej, co zdarza się raczej rzadko, błąd odczytu
nale

ży przyjąć za równy zeru.

Bezwzgl

ędny błąd odczytu dla przyrządu analogowego o równomiernej podziałce oblicza się

według poniższej formuły.

d

Z

p

p

od





gdzie:

od



- bezwzgl

ędny błąd odczytu

Zp -

zakres pomiarów

d -

liczba działek podziałki

p -

współczynnik charakteryzujący wprawę mierzącego.

Przyjmuje si

ę p = 0,1 przy starannym odczytywaniu wskazań, co oznacza, że mierzący może

pomyli

ć się w oszacowaniu położenia wskazówki maksymalnie o 0,1 wartości odpowiadającej

odległości między sąsiednimi wskazami podziałki.

Na przykład, jeżeli woltomierz o zakresie pomiarowym Zp = 15 V ma podziałkę równomierną
licz

ąca 75 działek, to odległości między dowolnymi dwiema sąsiednimi wskazami odpowiada

różnica napięć: 15V/75 = 0,2 V.

Przyjmuj

ąc współczynnik wprawy mierzącego p = 0,1 dostaniemy błąd odczytu

od



= 0,02 V.

Wzgl

ędny błąd odczytu

o d



oblicza si

ę, odnosząc błąd bezwzględny do wartości

wskazywanej W (iden

tycznie jak przy obliczaniu błędu wskazań):

%

100







W

od

od



=

%

100







W

d

Z

p

p

Całkowity maksymalny (graniczny) błąd pomiaru

Całkowity maksymalny (graniczny) błąd pomiaru jest sumą błędu wskazań i błędu odczytu.

Błędy te mogą mieć w ogóle przeciwne znaki i redukować się częściowo lub nawet całkowicie.
Znaki tych błędów jednak nigdy nie są znane, dlatego przyjmuje się zawsze skrajnie
niekorzystny przypadek i sumuje ich warto

ści bezwzględne.

Ocena dokładności średniej arytmetycznej wyników pomiarów

Aby zmniejszyć wpływ błędów przypadkowych na wynik pomiaru często dokonuje się w

ustalonych warunkach serii pomiarów x

1

, x

2

, x

3

, …, x

n

wartości danej wielkości, i oblicza się

wartość średnią :















n

i

i

n

x

n

x

x

x

n

x

1

2

1

1

)

...

(

1

Do

oceny błędu uzyskanej wartości używa się często błędu średniego średniej

arytmetycznej.

)

1

(

)

(

1

2











n

n

x

x

s

n

i

i