Interpolacja

1. Sformułowanie zagadnienia

2. Klasyczne zagadnienie interpolacji

3. Wielomian interpolacyjny Lagrange’a

4. Komenda w Maple’u

5. Interpolacja funkcjami sklejanymi

6. Komenda w Maple’u

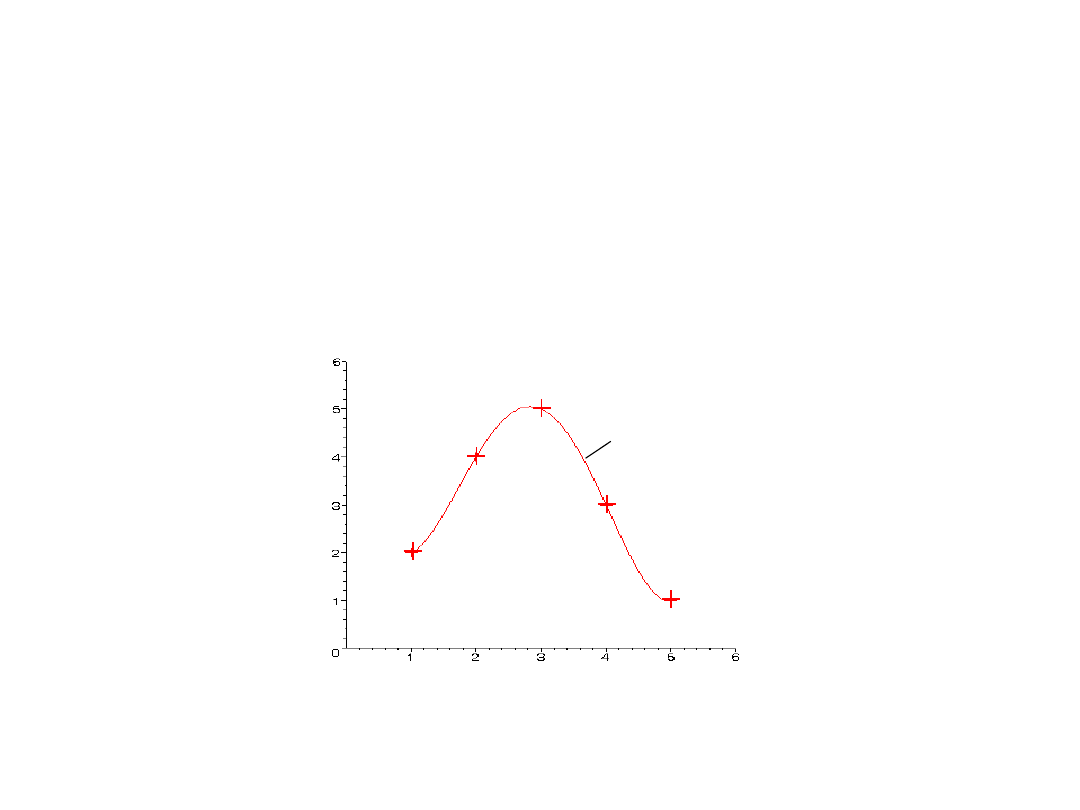
Sformułowanie zagadnienia

Interpolacja polega na znalezieniu wielomianu w(x), który przechodzić będzie
przez zadane punkty.



wielomian interpolacyjny

( )

w x

( )

y x

x

: (

,

),

0,1,...

: ( )

k

k

D

x y

k

n

Sz w x



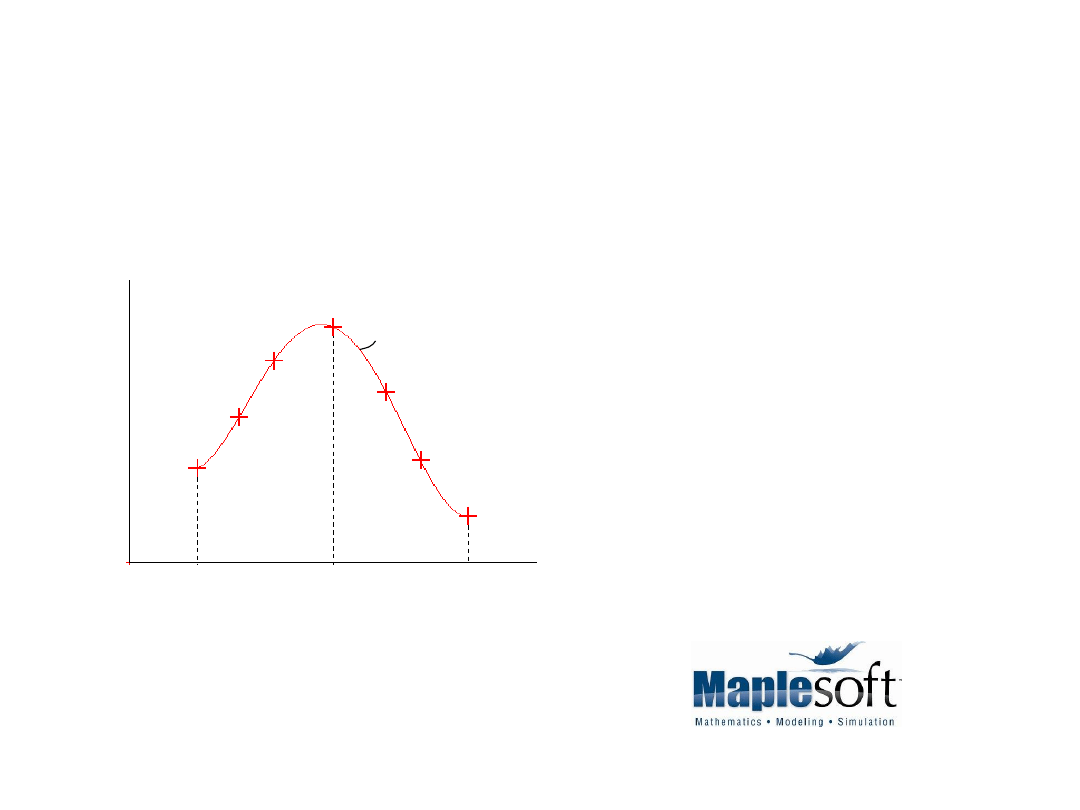
Klasyczne zagadnienie interpolacji

0

: (

,

),

0,1,...

: ( )

,

?

k

k

n

i

i

i

i

D

x y

k

n

Sz w x

a x

a





















































n

n

n

n

n

n

n

n

n

n

y

x

a

x

a

x

a

a

y

x

a

x

a

x

a

a

y

x

a

x

a

x

a

a

...

...

...

2

2

1

0

1

1

2

1

2

1

1

0

0

0

2

0

2

0

1

0



0

(

)

,

0..

n

i

k

i

k

k

i

w x

a x

y

k

n













,

...

,

,

,

,

2

1

0

n

a

a

a

a

0

x

n

x

i

x

x

( )

y x

)

(x

w

Wielomian interpolacyjny Lagrange’a

0

1

2

1

0

2

2

0

1

: ( ,

),

0,1, 2

: ( )

(

)(

)

(

)(

)

(

)(

)

k

k

D

x y

k

Sz w x

a x

x

x

x

a x

x

x

x

a x

x

x

x





















)

)(

(

,

)

)(

(

,

)

)(

(

1

2

0

2

2

2

2

1

0

1

1

1

2

0

1

0

0

0

x

x

x

x

y

a

x

x

x

x

y

a

x

x

x

x

y

a



















Koncepcja Lagrange’a na przykładzie wielomianu drugiego stopnia



























2

1

2

0

2

2

1

2

1

0

1

1

0

2

0

1

0

0

)

)(

(

)

)(

(

)

)(

(

y

x

x

x

x

a

y

x

x

x

x

a

y

x

x

x

x

a

)

)(

(

)

)(

(

)

)(

(

)

)(

(

)

)(

(

)

)(

(

)

(

1

2

0

2

1

0

2

2

1

0

1

2

0

1

2

0

1

0

2

1

0

x

x

x

x

x

x

x

x

y

x

x

x

x

x

x

x

x

y

x

x

x

x

x

x

x

x

y

x

w































Wielomian interpolacyjny Lagrange’a drugiego stopnia



rozprzęgnięty układ równań





k

k

y

x

w

)

(

Wielomian interpolacyjny Lagrange’a c.d.

)

)(

(

)

)(

(

)

)(

(

)

)(

(

)

)(

(

)

)(

(

)

(

1

2

0

2

1

0

2

2

1

0

1

2

0

1

2

0

1

0

2

1

0

x

x

x

x

x

x

x

x

y

x

x

x

x

x

x

x

x

y

x

x

x

x

x

x

x

x

y

x

w































Uogólnienie

- wielomian interpolacyjny

Lagrange’a n –tego stopnia

)

(

)

(

0

x

L

y

x

w

i

n

i

i







)

(

1

x

L

)

(

0

x

L

)

(

2

x

L

0

1

1

1

0

0

1

1

1

(

)

(

)(

)...(

)(

)...(

)

( )

(

)(

)...(

)(

)...(

)

(

)

n

j

i

i

n

i

j

i

i

i

i

i

i

i

n

i

j

j i

x

x

x

x

x

x

x

x

x

x

x

x

L x

x

x

x

x

x

x

x

x

x

x

x

x











































Komenda w Maple’u

interp(X,Y,nazwa)

X

– lista lub wektor wartości zmiennej niezależnej

Y

– lista lub wektor wartości zmiennej zależnej

nazwa – nazwa zmiennej niezależnej

> interp([0,1,2,3,4,5],[5,6,6,5,4,6],x);











5

29

20

x

11

24

x

2

1

24

x

3

1

24

x

4

1

120

x

5

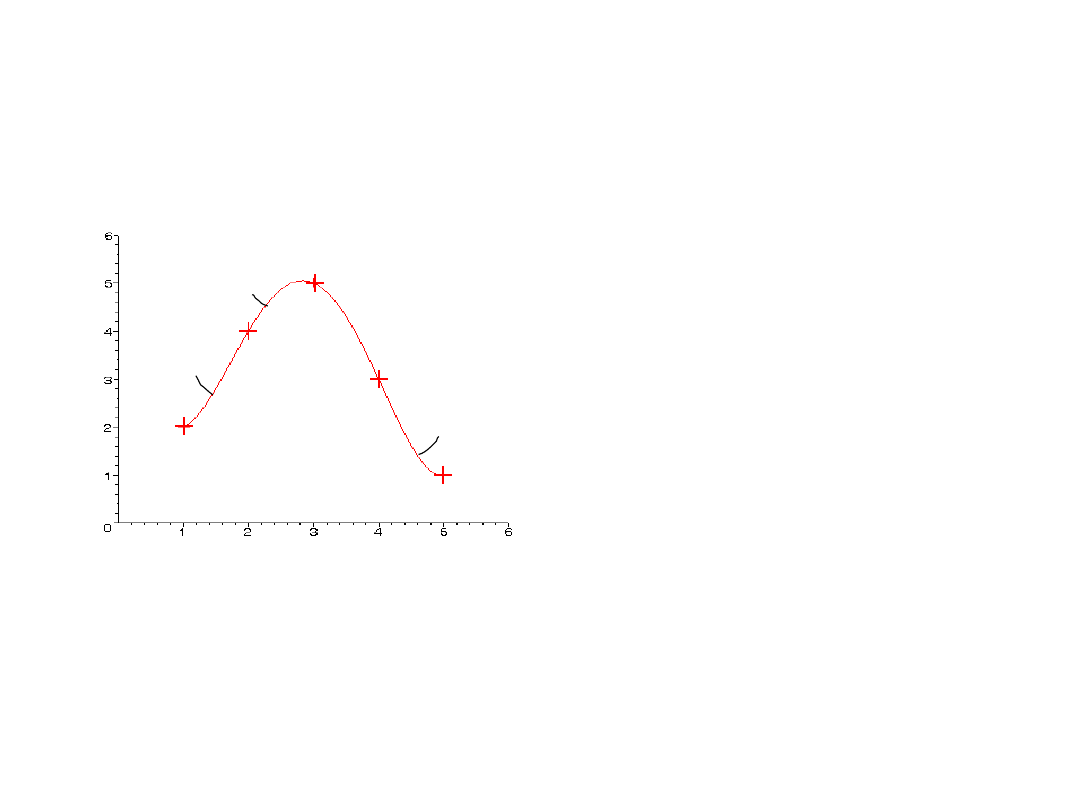
* Funkcjami sklejanymi (składanymi) nazywamy wielomiany małego stopnia (n<4),

opisujące zmienność funkcji y (x) w każdym z podprzedziałów (x

i

, x

i+1

) oddzielnie.

: (

,

),

0,1,...

: ( ),

1..

k

k

i

D

x y

k

n

Sz s x

i

n





Interpolacja funkcjami sklejanymi* (splines)

Interpolację funkcjami sklejanymi stosujemy
wtedy, gdy mamy dużą liczbę węzłów
interpolacyjnych i wielomian interpolacyjny
wykazuje nieuzasadnione oscylacje
pomiędzy węzłami (efekt Rungego)

)

(

1

x

s

)

(

2

x

s

)

(x

s

n

( )

y x

x

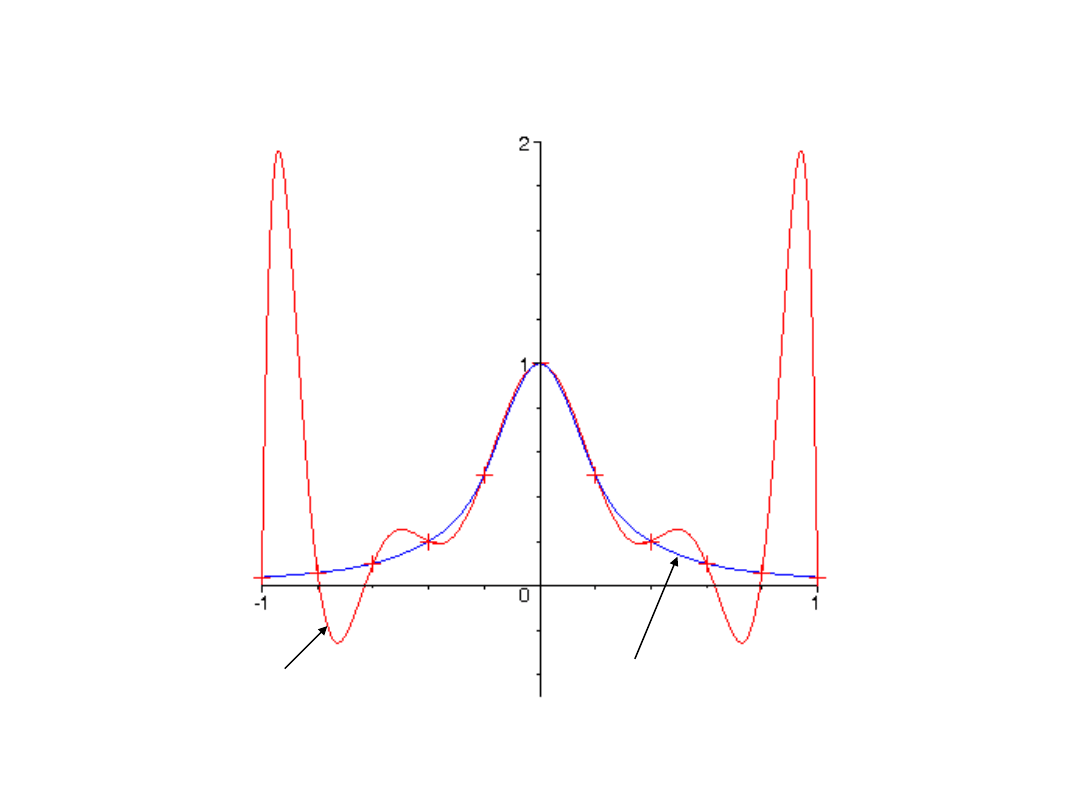
Interpolacja funkcjami sklejanymi c.d.

wielomian interpolacyjny

funkcje sklejane

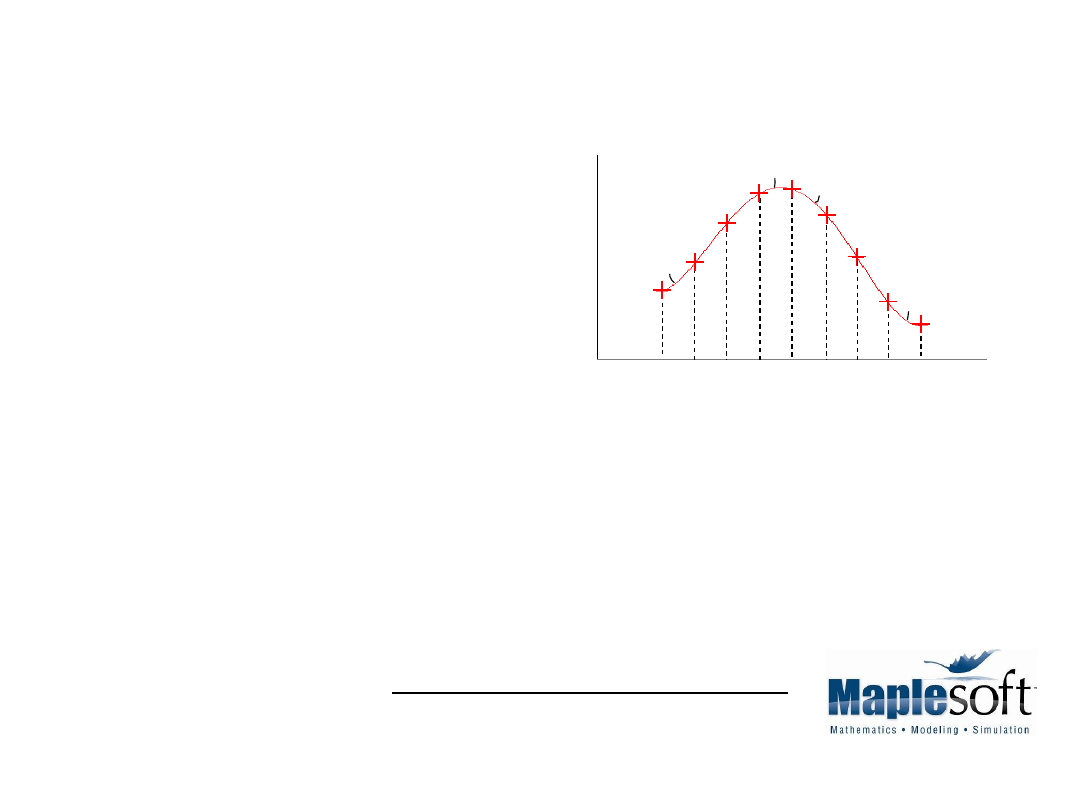
Interpolacja funkcjami sklejanymi c.d.

: (

,

),

0,1,...

: ( ),

1..

k

k

i

D

x y

k

n

Sz s x

i

n





n

i

x

d

x

c

x

b

a

x

s

Z

i

i

i

i

i

..

1

,

)

(

:

3

2











:

,

,

,

1..

(4 )

i

i

i

i

Sz a b c d

i

n

n



Warunki do spełnienia przez funkcje s

i

(x):

n

i

y

x

s

i

i

i

..

1

,

)

(





n

i

y

x

s

i

i

i

..

1

,

)

(

1

1









1

..

1

,

)

(

)

(

1













n

i

x

s

x

s

i

i

i

i

0

)

(

)

(

0

1









n

n

x

s

x

s

1

..

1

,

)

(

)

(

1













n

i

x

s

x

s

i

i

i

i

Razem: 4n równań

i

s

1



i

x

i

x

( )

y x

x

0

x

n

x

1



i

x

1



i

s

1

x

1

s

n

s

Komenda w Maple’u

Spline(X,Y,nazwa)

– komenda w pakiecie CurveFitting

X

– lista lub wektor wartości zmiennej niezależnej

Y

– lista lub wektor wartości zmiennej zależnej

nazwa – nazwa zmiennej niezależnej

> with(CurveFitting);

> Spline([0,1,2,3,4,5], [5,6,6,5,4,6], x);

























































5

23

19

x

4

19

x

3



x

1







90

19

2 x

15

19

x

2

1

19

x

3



x

2





98

19

26

19

x

9

19

x

2



x

3









388

19

512

19

x

9 x

2

18

19

x

3



x

4







1724

19

1072

19

x

225

19

x

2

15

19

x

3

otherwise