Przykład 1
Dany jest płaski układ czterech sił leżących w płaszczyźnie

Oxy

Obliczyć wektor główny i moment główny tego układu sił.

R o z w i ą z a n i e.
Wektor główny układu sił jest równy

Moment główny układu wynosi

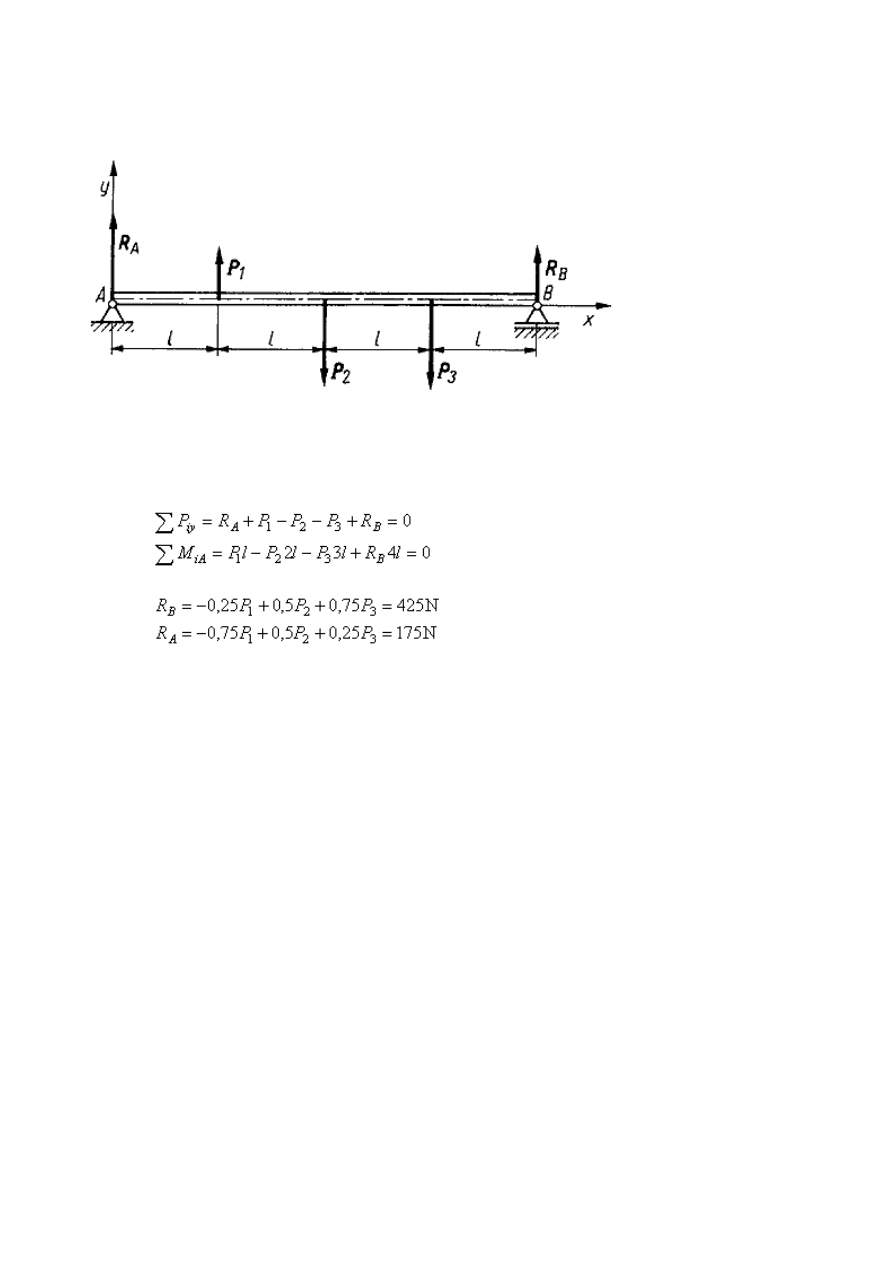
Przykład 2
Nieważka belka AB

= 4l została obciążona trzema siłami równoległymiP

1

,

P

2

, P

3

prostopadłymi

do belki. Znaleźć reakcje stałej podpory przegubowej w punkcie A i podpory przegubowej
przesuwnej w punkcieB. Dane liczbowe: P

1

= 100 N, P

2

= 300 N, P

3

= 400 N, l = 1 m.

R o z w i ą z a n i e.
Reakcje w podporach A

i B

maja kierunek pionowy. Na belkę działa układ pięciu sił

równoległych P

1

,

P

2

, P

3

, R

A

i R

B

. Dwie niewiadome reakcje R

A

i R

B

wyznacz

a się z dwóch równań

równowagi

Stąd

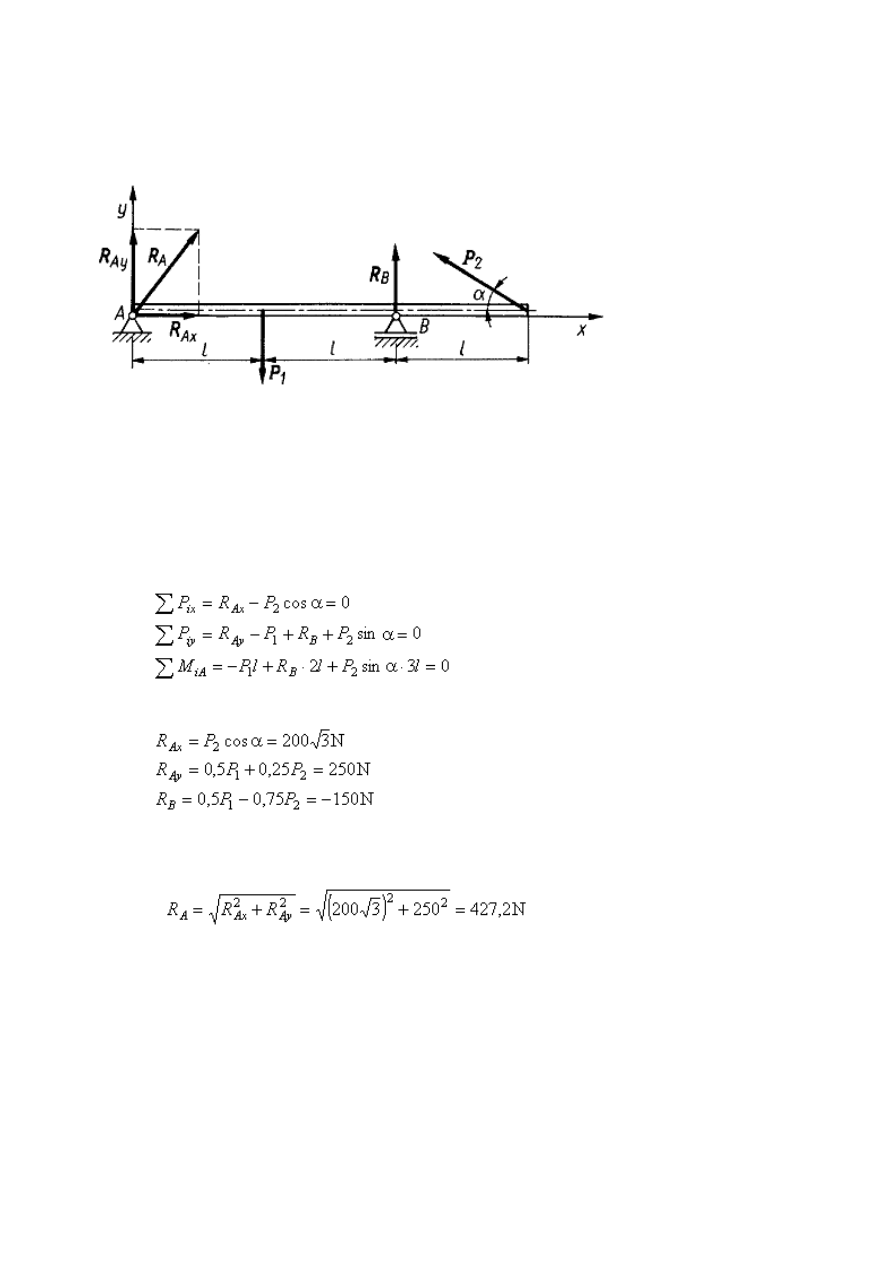
Przykład 3
Nieważka belka AB

= 3l jest zamocowana w punkcie A na stałej podporze przegubowej, a w

punkcie B na podporze przegubowej przesuwnej. Obciążenie belki stanowią siły P

1

= 300

N i P

2

= 400 N, a kąt





= 30º. Obliczyć reakcje w punktach podparcia A i B.

R o z w i ą z a n i e.
Kierunek reakcji R

A

w stałej podporze przegubowej A nie jest znany, wiadomo tylko, że linia

działania tej siły przechodzi przez środek przegubu A. Reakcję tę rozkłada się na dwie
składowe wzdłuż osi prostokątnego układu współrzędnych

Axy

. Składowe reakcji R

A

zostały

oznaczone przez R

Ax

i R

Ay

. Zatem, belka jest obciążona dwoma siłami zewnętrznymi P

1

i

P

2

oraz

trzema reakcja

mi więzów R

Ax

, R

Ay

i R

B

. Wartości tych reakcji wyznacza się z trzech równań

równowagi

Z rozwiązania powyższego układu trzech równań z trzema niewiadomymi otrzymamy

Reakcja R

B

jest ujemna, stąd jej kierunek jest przeciwny niż założono na rysunku.

Wartość reakcji

R

A

oblicza się ze wzoru

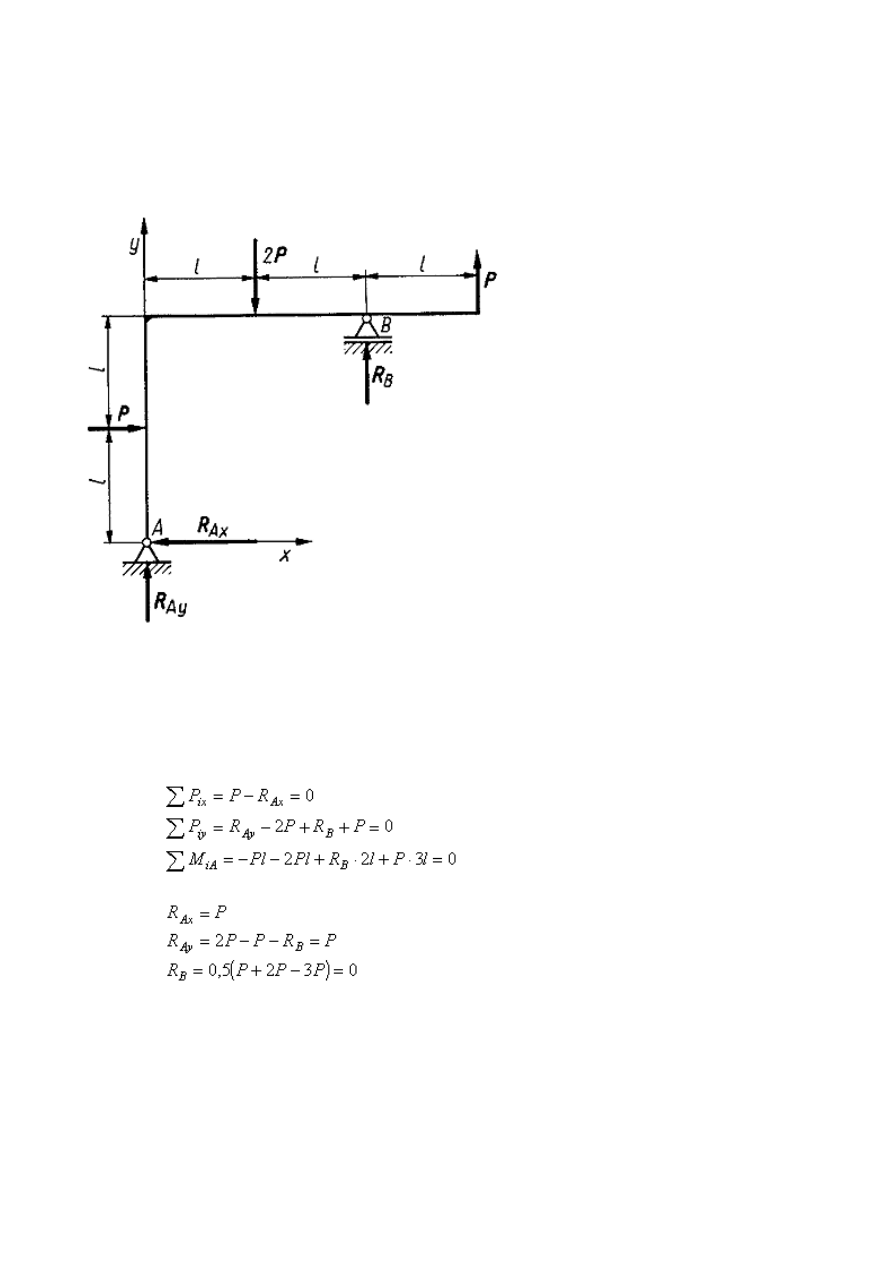
Przykład 4
Nieważka rama płaska została zamocowana na stałej podporze przegubowej w
punkcie A i podporze przegubowej przesuwnej w punkcieB. Obciążenie zewnętrzne
ramy stanowią siły

P

i siła 2

P

. Obliczyć reakcje podpór

R

A

i R

B

, jeżeli

P = 1000 N, l

= 0,5 m

.

R o z w i ą z a n i e.
Rama jest obciążona trzema siłami zewnętrznymi

i reakcjami

R

A

i R

B

. Ponieważ

kierunek reakcji

R

A

jest nie znany, dlatego r

ozkłada się ją na dwie składowe

R

Ax

, R

Ay

.

Niewiadome reakcje wyznacza się z trzech równań równowagi ramy

Stąd

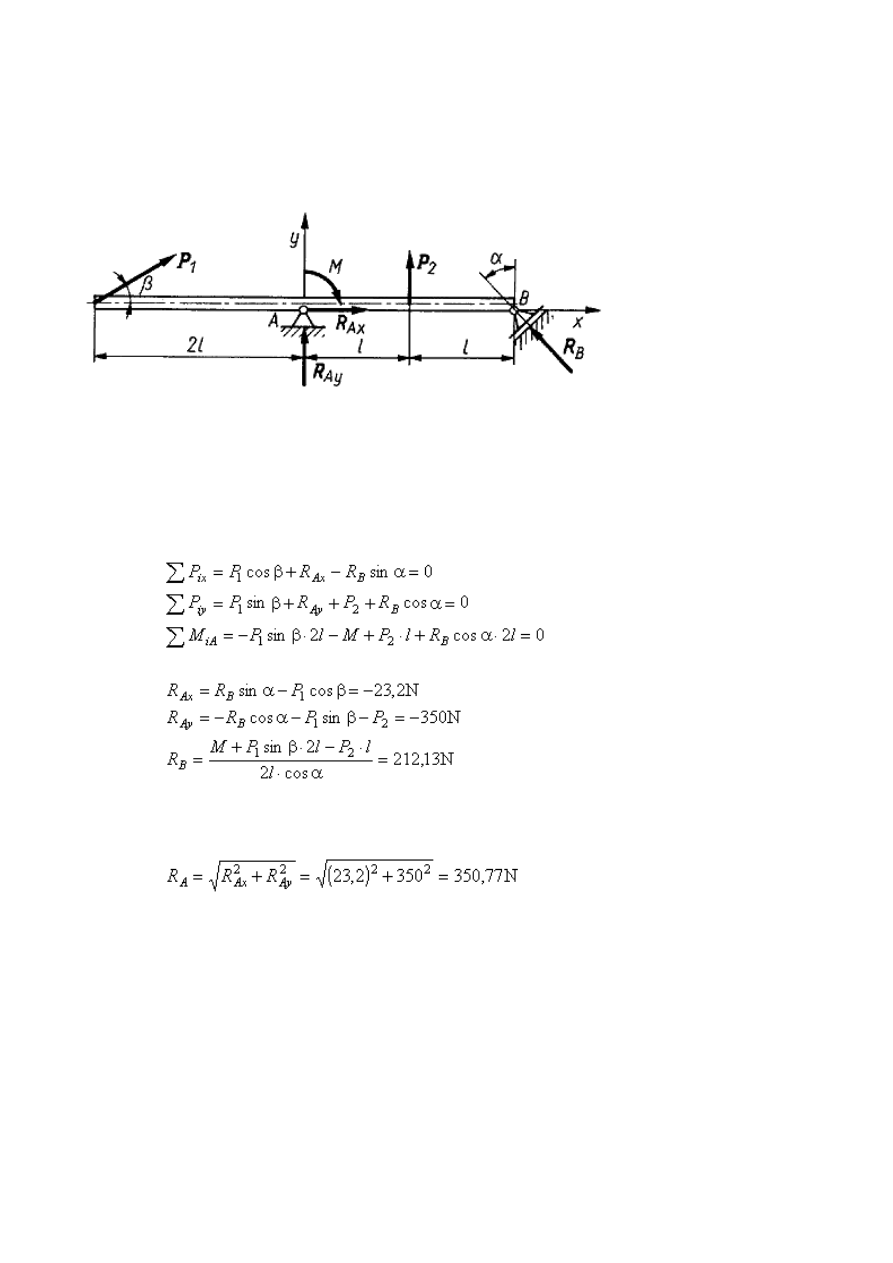
Przykład 5
Obliczyć reakcje podpór A i B w belce pokazanej na rysunku. Obciążenie zewnętrzne
sta

nowią dwie siły

P

1

= 200 N, P

2

= 100 N

i moment

M = 200 N · m

. Pozostałe dane

liczbowe wynoszą:

l = 1 m,





= 45º,





= 30º.

R o z w i ą z a n i e.
Belka jest obciążona dwiema siłami zewnętrznymi

P

1

,

P

2

, momentem Moraz

reakcjami R

A

i R

B

. Ponieważ kierunek reakcji

R

A

jest nie znany, dlatego rozkłada się ją

na dwie składowe

R

Ax

, R

Ay

. Niewiadome reakcje wyznacza się z trzech równań

równowagi

Stąd

Reakcje

R

Ax

, R

Ay

są ujemne, stąd ich kierunek jest przeciwny do założonego. Wartość

reakcji

R

A

wynosi

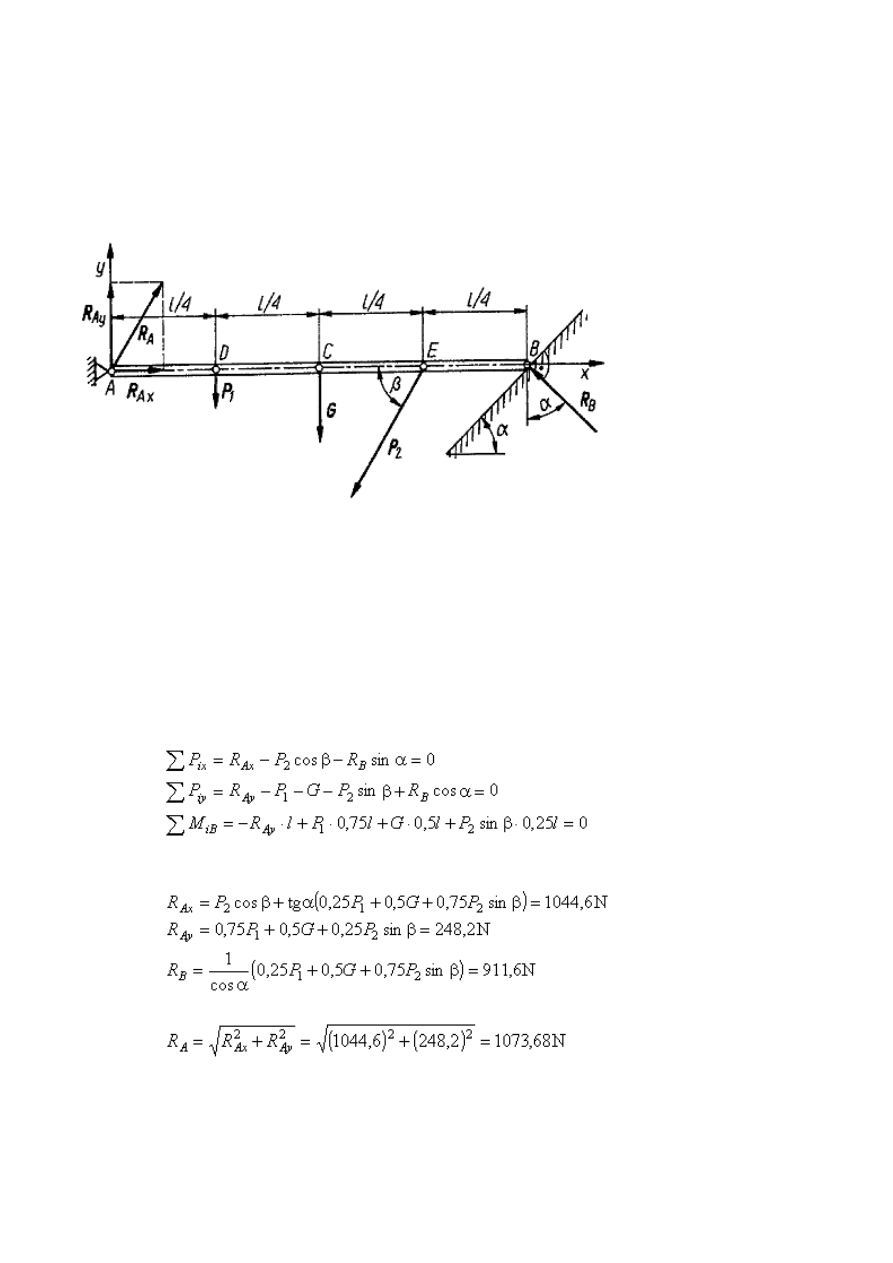
Przykład 6
Jednorodna pozioma belka AB o ciężarze równym G jest oparta końcemA na stałej
podporze przegubowej oraz końcem B na gładkiej równi pochyłej. W
punktach D i E do belki przyłożone są siły

P

1

,

P

2

. Obliczyć reakcje w punktach

podparcia A i B. Dane liczbowe:

P

1

= 100 N, P

2

= 800 N, G = 200 N,





= 45º,





= 60º, l = 4 m

.

R o z w i ą z a n i e.
Oddziaływanie równi na koniec belki B, czyli reakcja

R

B

więzów będzie prostopadła do

płaszczyzny tej równi. Wynika to z faktu, że siła tarcia między płaszczyznami równi i
belki równa się zeru. Kierunek reakcji

R

A

w przegubie A nie jest znany, wiadomo tylko,

że linia działania tej siły przechodzi przez środek przegubu, tj. przez punkt A.
Reakcję tę rozkładamy na dwie składowe

R

Ax

, R

Ay

wzdłuż osi prostokątnego układu

współrzędnych Axy. Tak więc belka jest obciążona trzema siłami zewnętrznymi i
trzema reakcjami. Wyznaczamy wartości tych reakcji z trzech równań równowagi

Rozwiązując powyższy układ równań otrzymujemy

Stąd

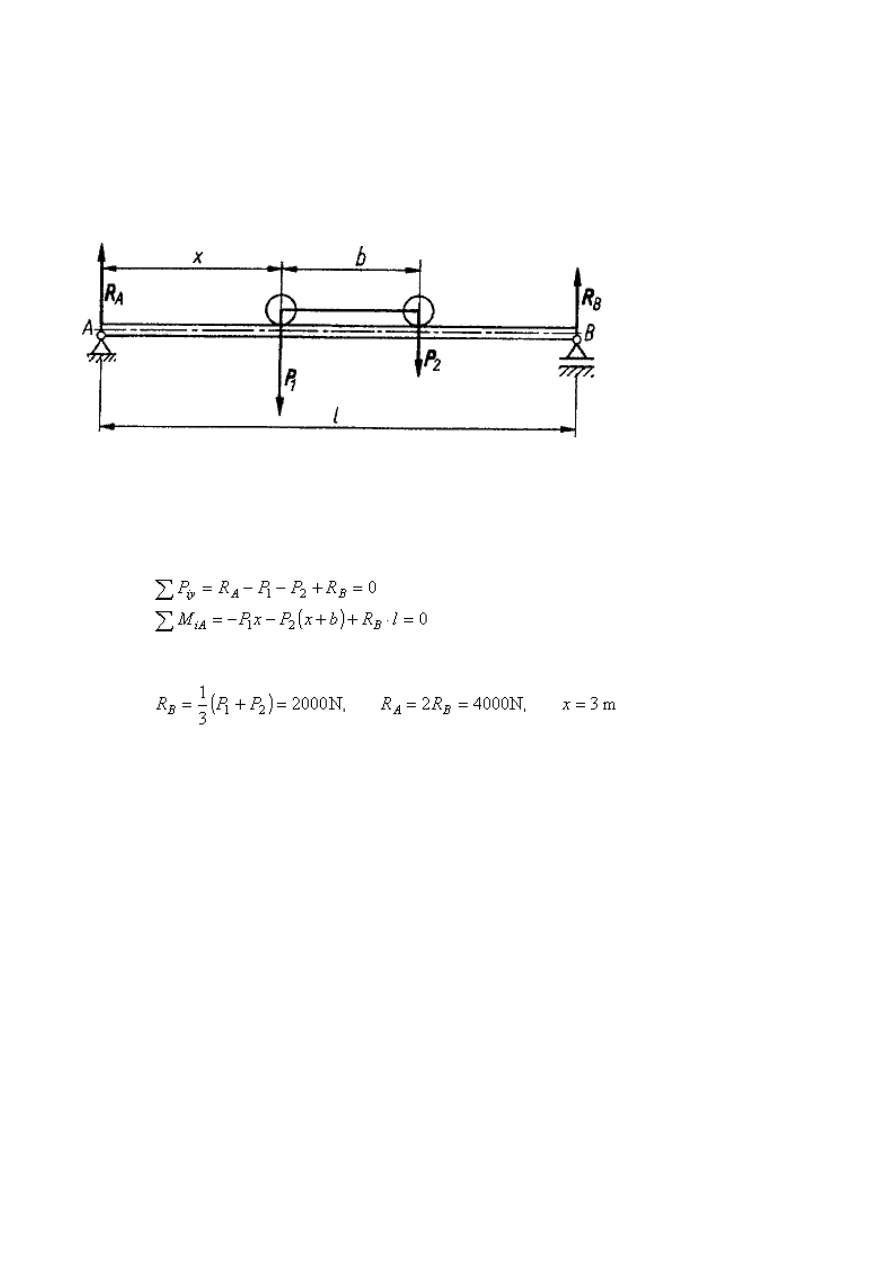
Przykład 7
Po belce podsuwnicowej AB porusza się suwnica, której wózek, składający się z
dwóch kół tocznych, oddziałuje na belkę siłami

P

1

,

P

2

.

W jakiej odległości x od

punktu A powinien wózek się zatrzymać, aby reakcja w punkcie B była dwukrotnie
mniejsza od reakcji w punkcie A ? Dane liczbowe:

P

1

= 4000 N i P

2

= 2000 N, b = 1 m, l

= 10 m

.

R o z w i ą z a n i e.
Ponieważ siły

P

1

,

P

2

, działające na belkę, są pionowe oraz reakcja

R

B

ma kierunek

pionowe, również reakcja R

A

ma kierunek pionowy. Piszemy dwa równania równowagi

Po rozwiązaniu tego układu równań, przy założeniu, że R

B

= 0,5R

A

, otrzymujemy

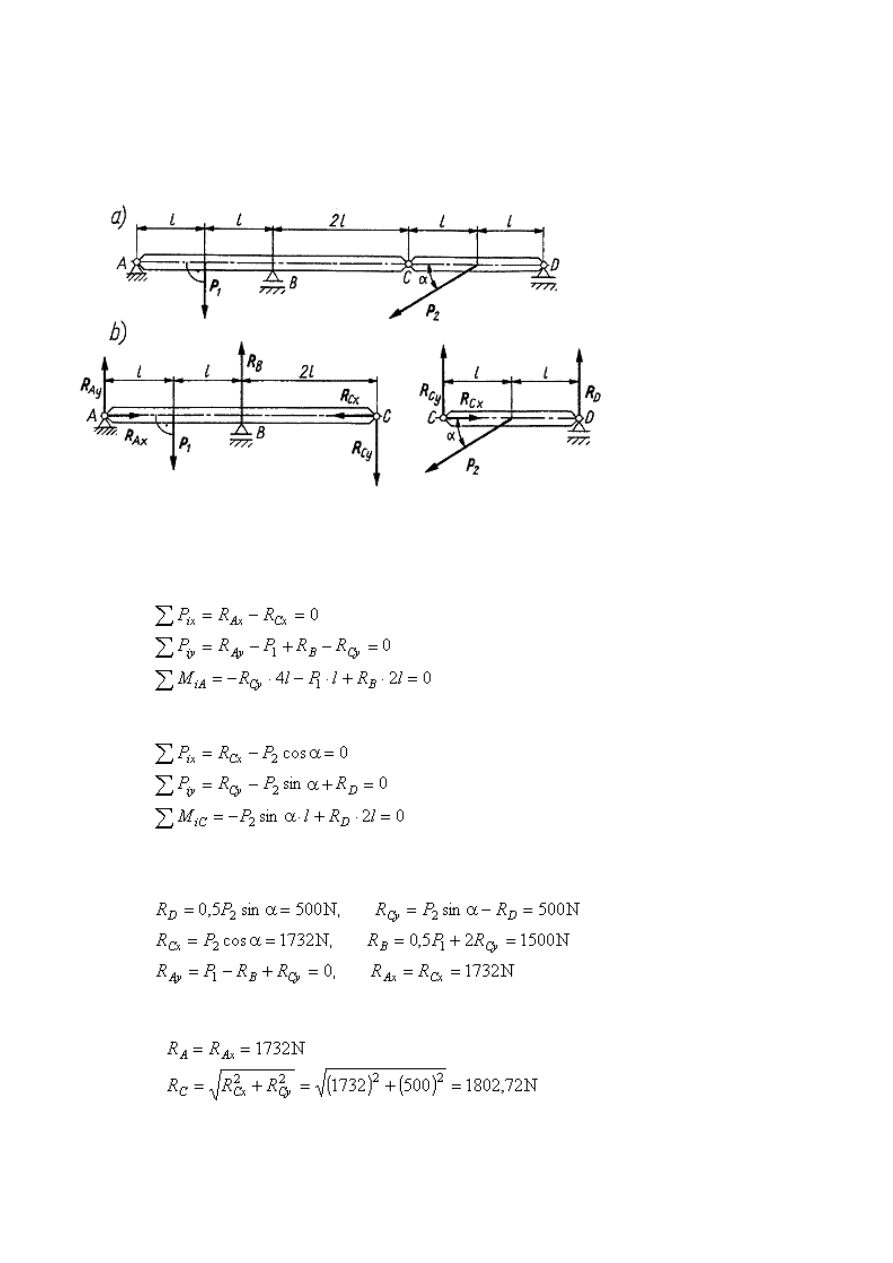
Przykład 8
Wyznaczyć reakcje podpory przegubowej stałej A i dwóch podpór przegubowych
przesuwnych B i D oraz wzajemne oddziaływanie w przegubie C obydwu części belki ABCD.
Dane liczbowe: P

1

= 1000 N,

P

2

= 2000 N,





= 30º, l = 1 m.

R o z w i ą z a n i e.
W celu wyznaczenia reakcji

R

A

, R

B

, R

C

i R

D

rozważymy równowagę obu części belki.

Równania równowagi lewej części belki mają postać

Równania równowagi prawej części belki

Otrzymaliśmy układ sześciu równań równowagi z sześcioma niewiadomymi. Po rozwiązaniu
tego układu otrzymujemy

Reakcje R

A

i R

C

wynoszą

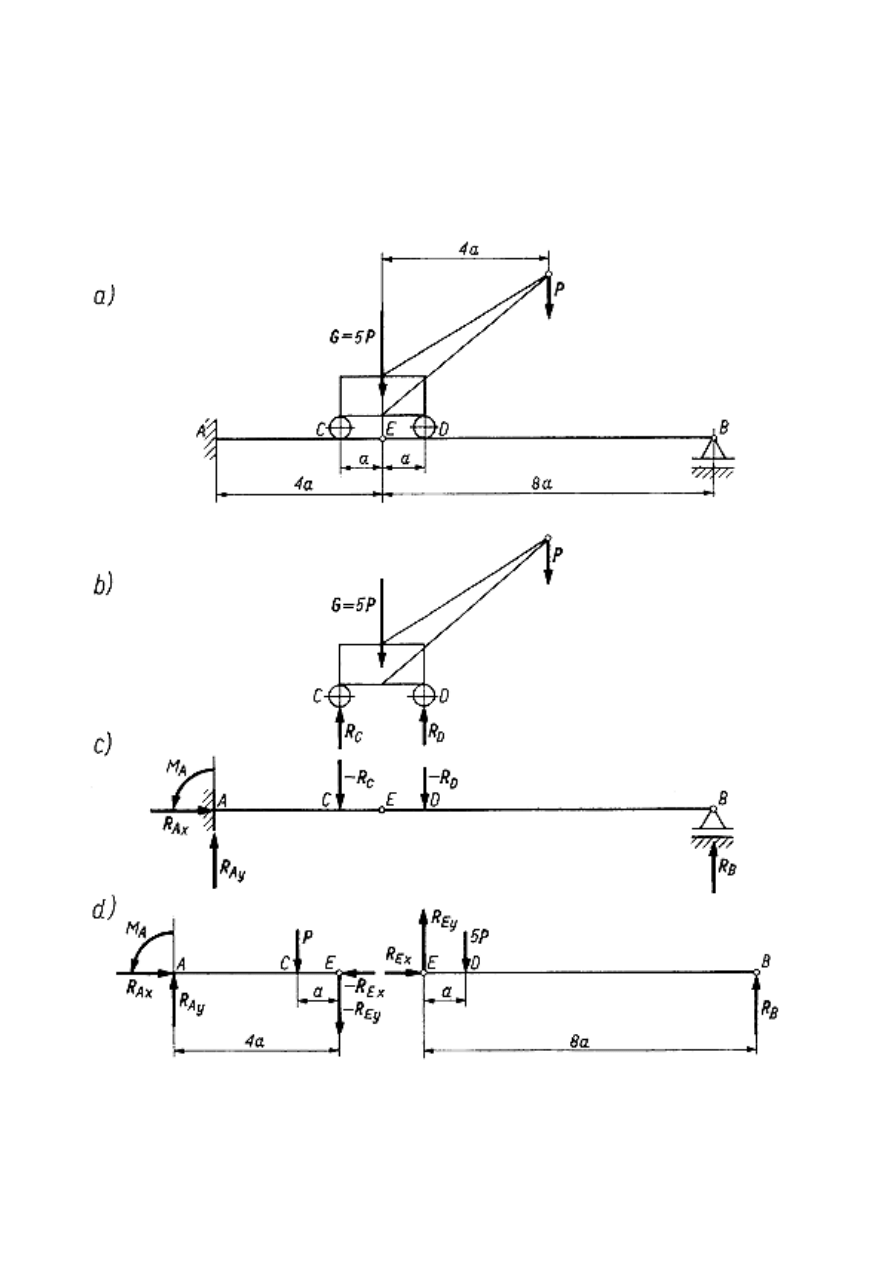
Przykład 9
Dźwig o ciężarze własnym G = 5P, obciążony na wysięgniku siłą P, zainstalowano na
torze jezdnym AB. Obliczyć reakcje kół dźwigu, reakcje utwierdzenia całkowitego w
punkcie A i podpory przegubowej przesuwnej w punkcie B oraz reakcję w
przegubie E, jeżeli AE = 4a,
BE = 8a, CE = DE = a.

R o z w i ą z a n i e.
Reakcje utwierdzenia całkowitego w punkcie A sprowadzają się do reakcji

R

A

o nie

znanym kierunku oraz momentu utwierdzenia M

A

. W podporze przegubowej

przesuwnej w punkcie B i podporach kół dźwigu w punkcie C i D występują reakcje o
kierunku pionowym, prostopadle do płaszczyzny poziomej (przesuwu). Reakcja
przegubu E sprowadza się do siły o nie znanym kierunku działania, przechodzącej
przez oś tego przegubu. Z dwóch równań równowagi dźwigu (rys. b) wyznaczamy
reakcje

R

C

i R

D

podpór jego kół

Stąd

Równania równowagi dwóch części belki AB, zgodnie z rys. d są następujące:



część belki BE



część belki AB

Po rozwiązaniu tego układu otrzymujemy