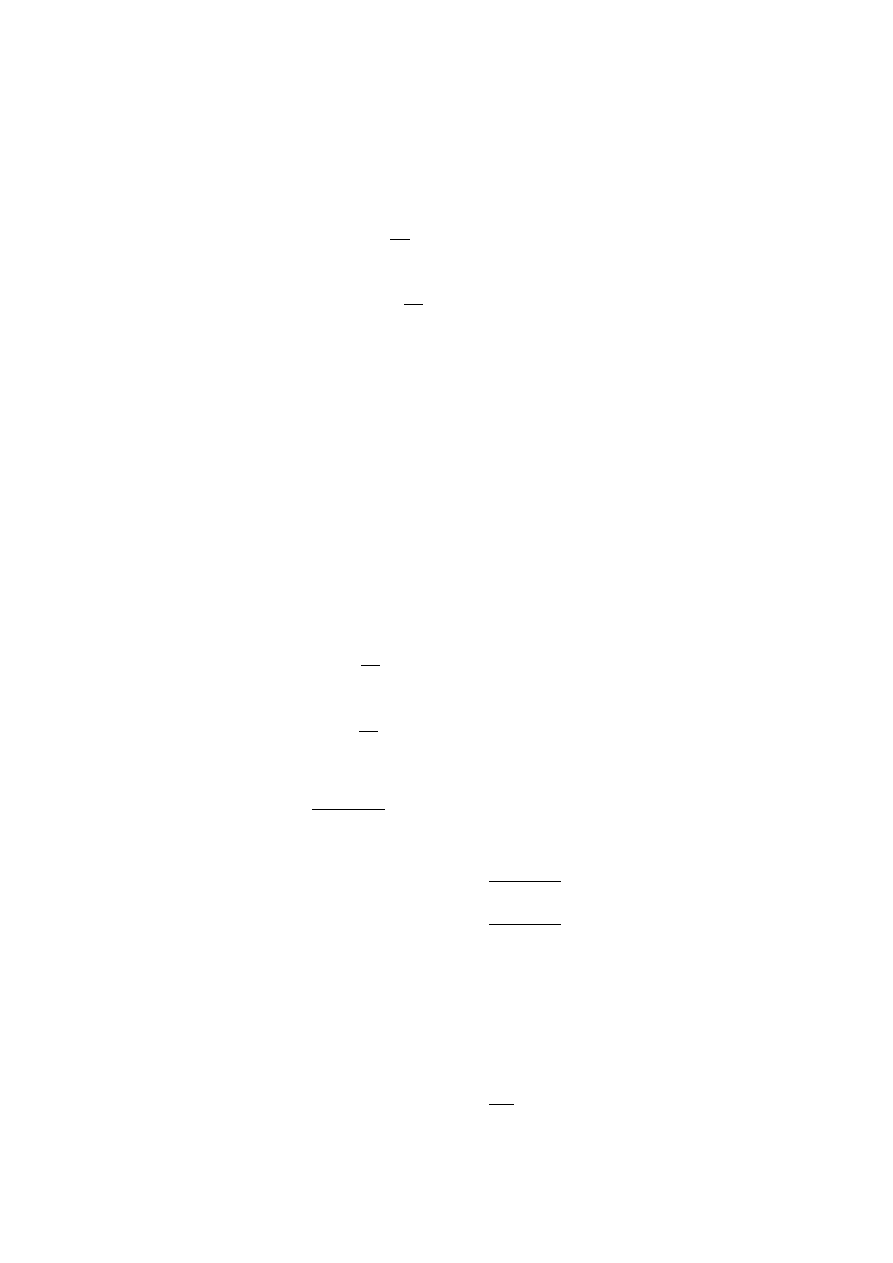
Kinematyka
1. Otrzymad wzory na prędkośd i położenie w jednowymiarowym ruchu jednostajnie przyspieszonym.
Ponieważ ruch jest jednostajnie przyspieszony mamy:
v
0
– prędkośd początkowa
t
0
– czas początkowy
dla t
0
= 0 mamy:
v
0
– prędkośd początkowa
t
0
– czas początkowy
x
0
– położenie początkowe
dla t
0
= 0 mamy:
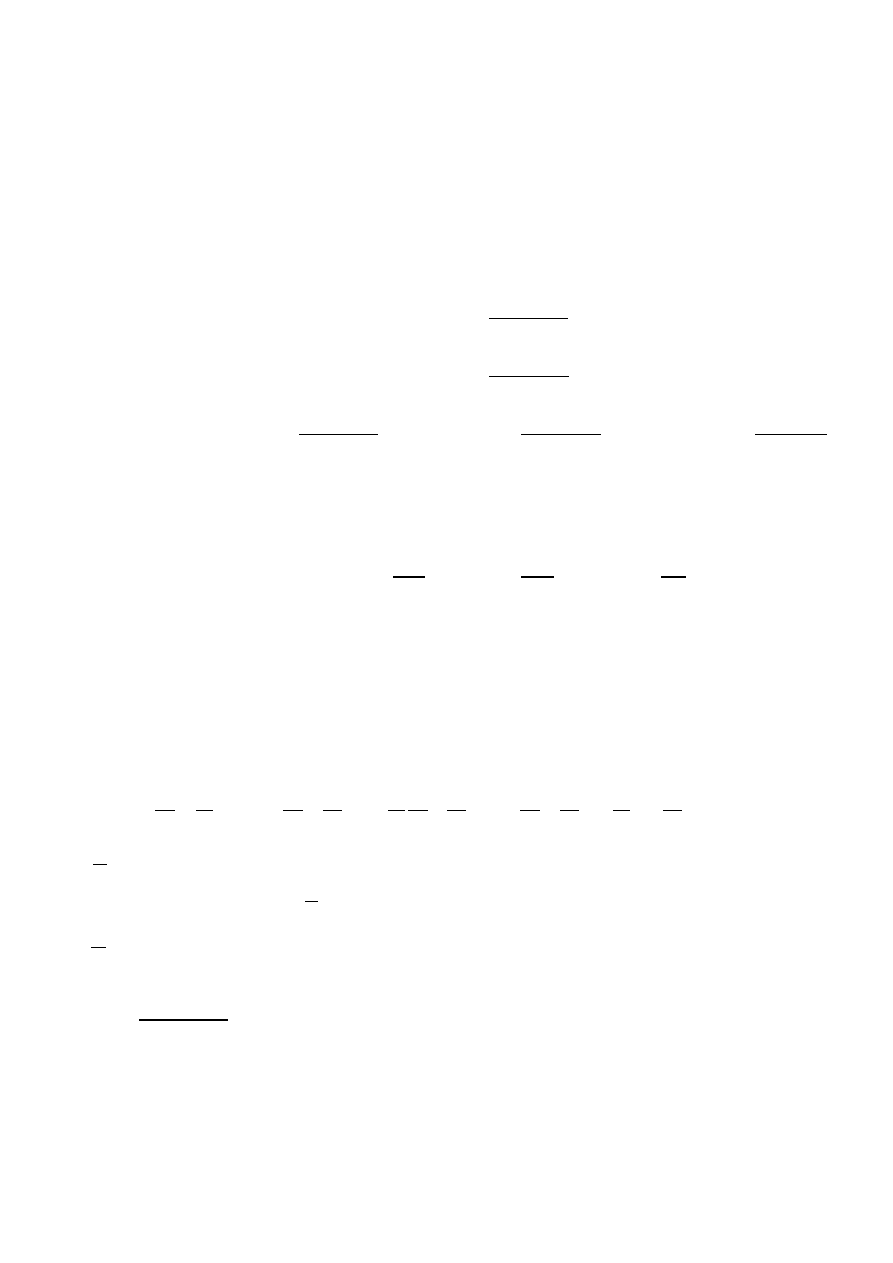
2. Otrzymad wzory na prędkośd i położenie w dwuwymiarowym ruchu jednostajnie przyspieszonym.
Są to dwa niezależne(prostopadłe do siebie) jednowymiarowe ruchy jednostajnie przyspieszone.
Dla t
0
= 0:
3. Przyspieszenie styczne i normalne na przykładzie ruchu po okręgu ze stałą szybkością.
Wprowadźmy oznaczenia:
- jednostkowy wektor styczny do toru ruchu
- jednostkowy wektor normalny do toru ruchu
s – długośd toru ruchu
- promieo krzywizny toru ruchu
- przyspieszenie normalne (dośrodkowe)
dla ruchu po okręgu :
- przyspieszenie styczne