Różniczkując równanie prędkości mamy:

Z tego wynika, że jeśli S jest inercjalnym układem odniesienia to S’ również.

We wszystkich przekształceniach przyjęliśmy dodatkowe założenie absolutnego czasu t’=t.

Praca i energia

1. Policz pracę wykonaną przez siłę sprężystości przy przesunięciu ciała z położenia xi do położenia xf.

Siła sprężystości jest określona przez prawo Hooke’a. Jeśli sprężyna jest ściśnięta lub rozciągnięta o małą długośd x
względem swojego stanu równowagi (x=0), to wywiera ona siłę gdzie k jest dodatnią stałą materiałową
nazywaną stałą sprężystości.
Przesuwając ciało z położenia xi do xf siła sprężystości wykona pracę:

Jeśli xi = xf to W = 0.

2. Policzyd pracę jaką należy wykonad przyspieszając do prędkości v spoczywającą swobodną cząstkę o masie m,
czyli wyprowadzid wzór na nierelatywistyczną energię kinetyczną.

Dla v

p

= 0 i v

k

= v mamy:

3. Podaj trzy równoważne definicje siły potencjalnej.

Siła jest siłą potencjalną jeśli istnieje funkcja (skalarna) taka, że:

Gdzie:

Funkcję U nazywamy energią potencjalną siły .

Ponieważ przesunięcia odbywają się w jakimś czasie, więc

Siła potencjalna jest wtedy i tylko wtedy gdy praca wykonana przez między dwoma dowolnymi punktami nie zależy
od drogi wykonanej między tymi punktami (łączącej te punkty) a jedynie od położeo tych punktów (początkowego i
koocowego).

Siła jest potencjalna wtedy i tylko wtedy gdy praca tej siły na dowolnej drodze zamkniętej jest równa zeru.

4. Napisz równanie wiążące siłę z energią potencjalną.

Siła musi byd jednoznacznie określona w przestrzeni X,Y,Z

Gdzie:

Funkcję U nazywamy energią potencjalną siły .

Ponieważ przesunięcia odbywają się w jakimś czasie, więc

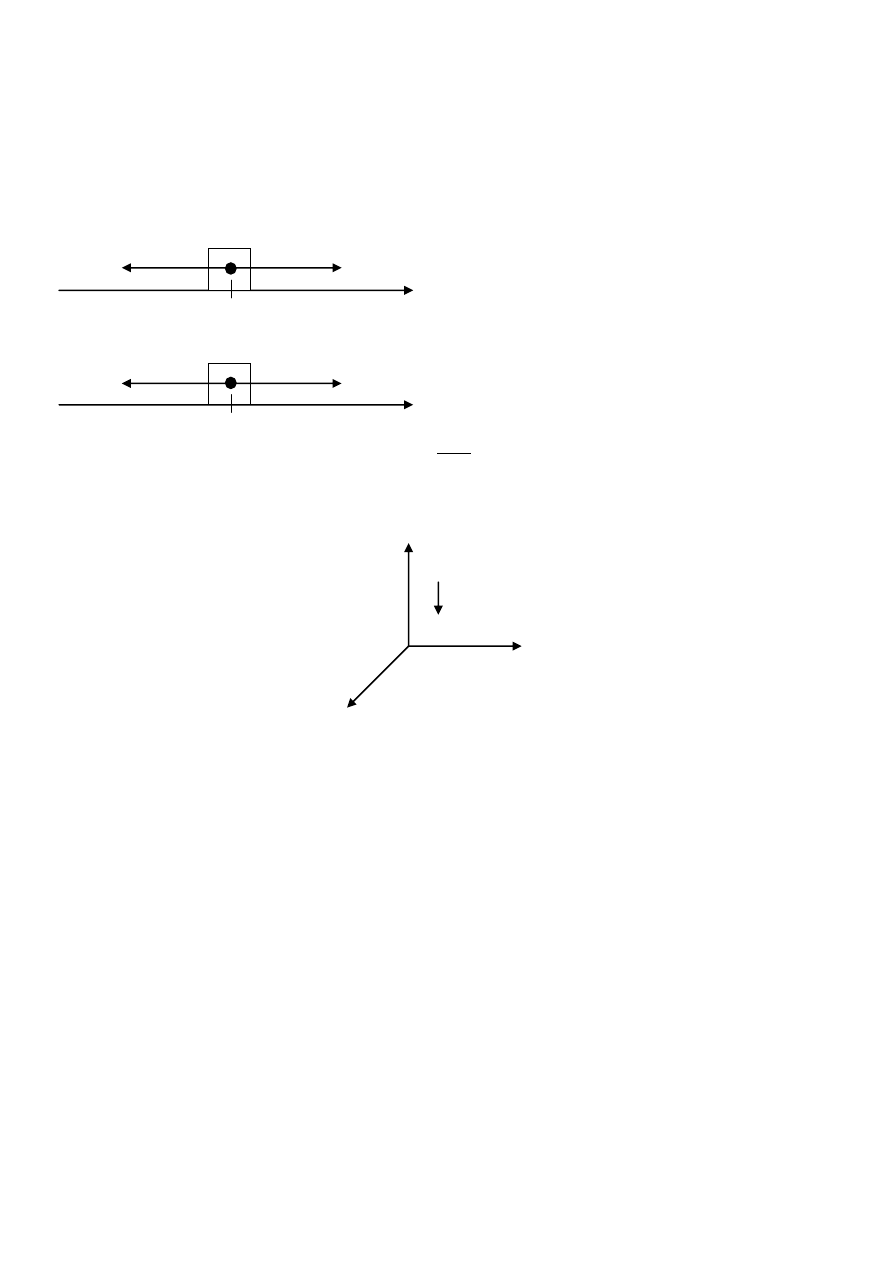
5. Pokaż, że siła tarcia nie jest siłą potencjalną.

Chod siła tarcia jest całkowalna:

To nie jest jednoznacznie określona w przestrzeni X:

zależy od prędkości w x

0

i nie ma takiej funkcji U(x), że

.

Wszystkie siły zależne od prędkości nie są siłami potencjalnymi.

6. Znajdź energię potencjalną jednorodnego pola grawitacyjnego.
Siła działająca na masę m:

Energia potencjalna:

Najlepiej przyjąd z

0

= 0 i

. Mamy wtedy:

7. Znajdź energię potencjalną siły sprężystości.

Siła sprężystości jest siłą centralną:

Gdzie jest wektorem odchylenia z położenia równowagi, , a k jest współczynnikiem sprężystości (stałą
materiałową).

Energia potencjalna:

x

x

0

x

x

0

x

y

z

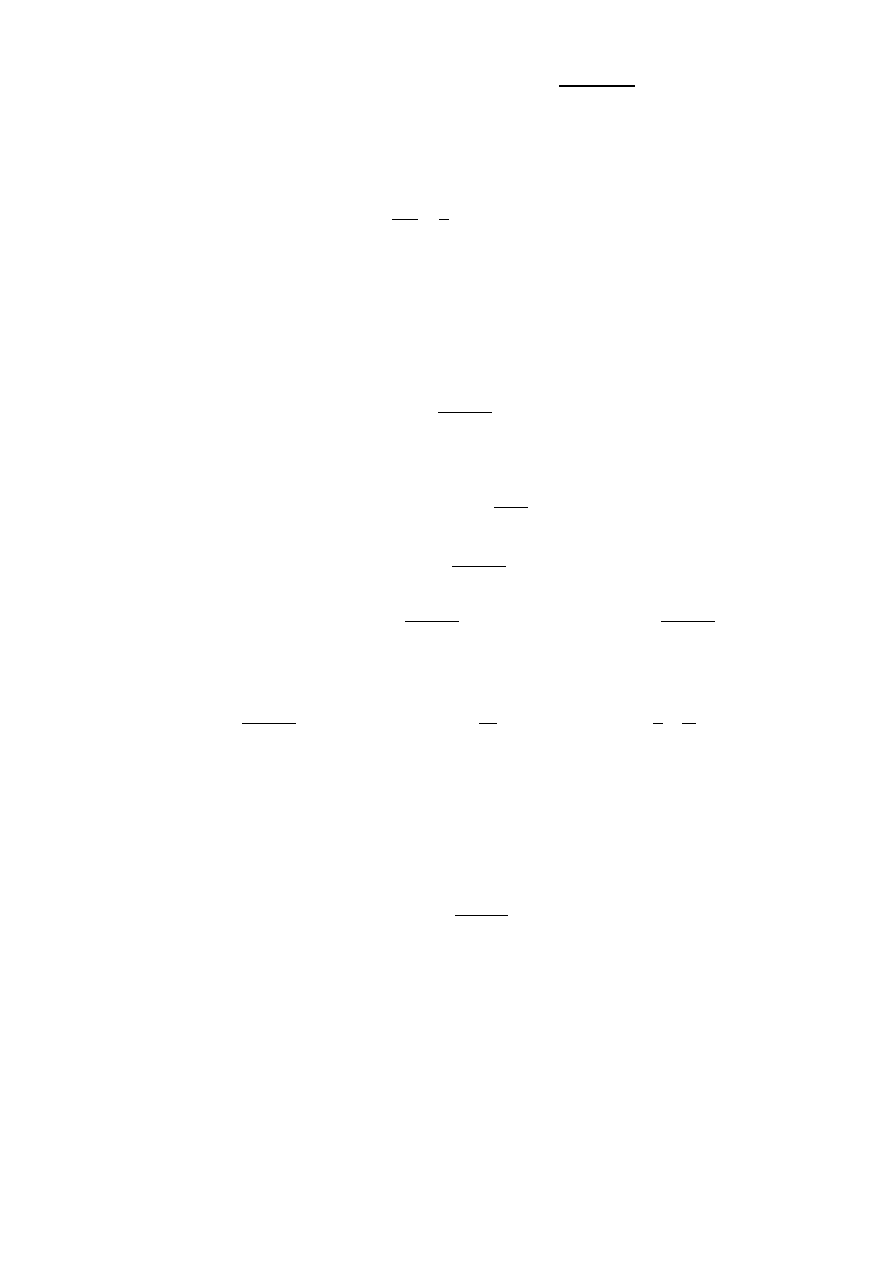
Fizycznie naturalne określenie

i

to

= 0 i

- układ jest w stanie równowagi, nie jest odkształcony,

więc nie działa siła sprężystości i nie ma związanej z nią energii potencjalnej. Wtedy:

8. Pokazad, że siła grawitacji jest siłą potencjalną i znaleźd grawitacyjną energię potencjalną układu dwóch mas
m1, m2 znajdujących się w odległości r.

Siła grawitacji:

Uniwersalna stał grawitacji:

Energia potencjalna układu dwóch mas m1, m2:

Praca wykonana przez między dwoma dowolnymi punktami nie zależy od drogi wykonanej między tymi punktami
(łączącej te punkty) a jedynie od położeo tych punktów (początkowego i koocowego) zatem siła grawitacji jest siłą
potencjalną.

Jako punkt odniesienia przyjmujemy bo tam siła grawitacji zanika:

wtedy:

9. Zasada zachowania energii mechanicznej.

Energia mechaniczna = energia kinetyczna + energia potencjalna

Praca wykonana przez siłę zachowawczą przy przesunięciu cząstki z położenia

do położenia

.

A z twierdzenia o pracy i energii

Więc:

Czyli:

Energia mechaniczna cząstki w polu sił potencjalnych jest stała.

10. Zasada zachowania energii mechanicznej układu dwóch mas m, M oddziałujących grawitacyjnie. Rozważyd
przypadek M>>m.

Z zasady zachowania energii mechanicznej:

Jeśli

a na układ mas nie działają siły zewnętrzne mamy =>

Całkowity pęd układu:

Więc możemy przyjąd :

A wtedy:

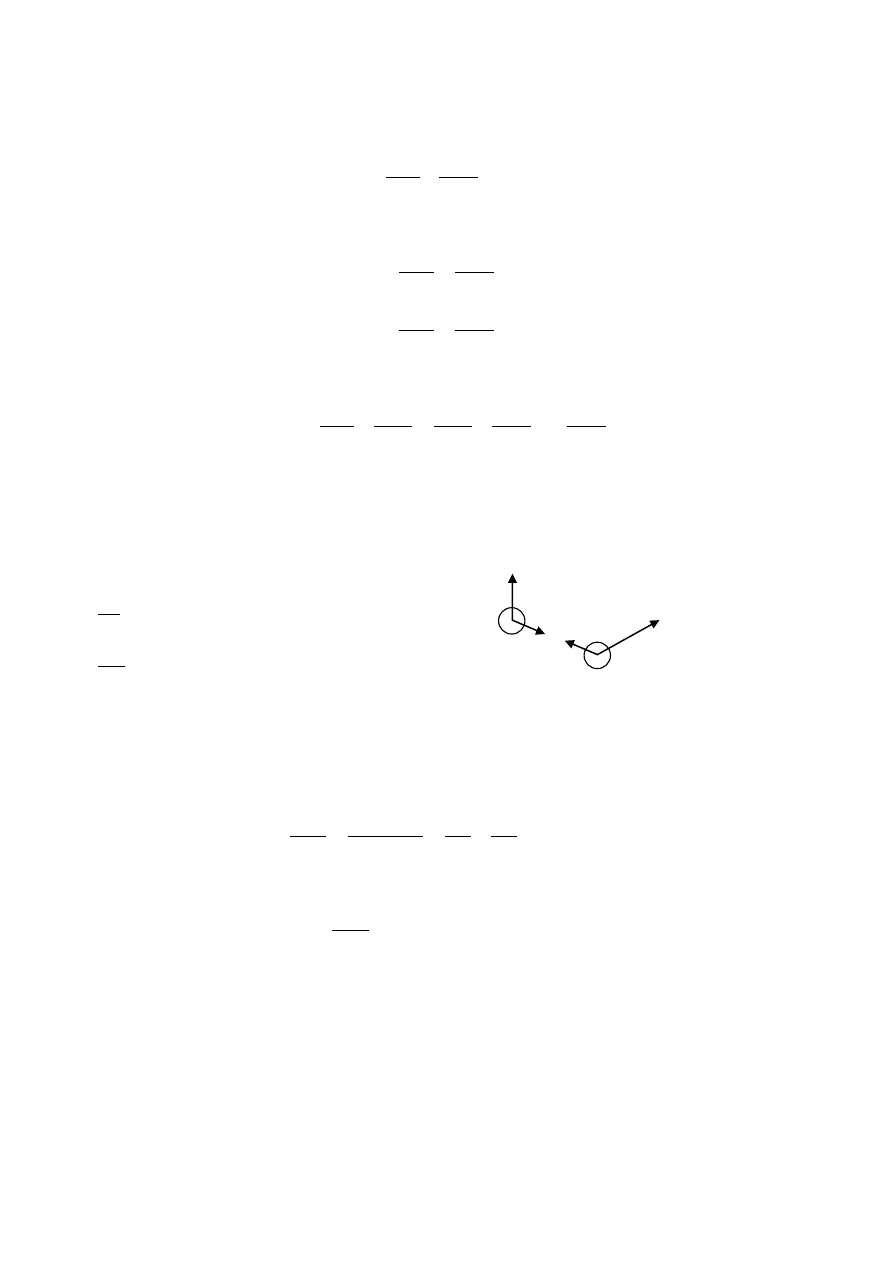
11. Planeta o masie m krąży wokół gwiazdy o masie M (M>>m) po orbicie kołowej o promieniu r. Znaleźd
całkowitą energię mechaniczną tego układu mas

Z zasady zachowania energii mechanicznej z uwzględnieniem :

Skoro planeta porusza się po orbicie kołowej, to siła grawitacji pełni rolę siły dośrodkowej i jest równa:

I wtedy:

Zasada zachowania pędu

1. Pokazad, że pęd izolowanego układu dwóch cząstek, które oddziałują ze sobą siłami wewnętrznymi jest
zachowany.

Całkowity pęd układu cząstek to suma (wektorowa) pędów poszczególnych cząstek:

I zmiana

w czasie:

A z trzeciej zasady dynamiki mamy

, zatem

, a w takim razie:

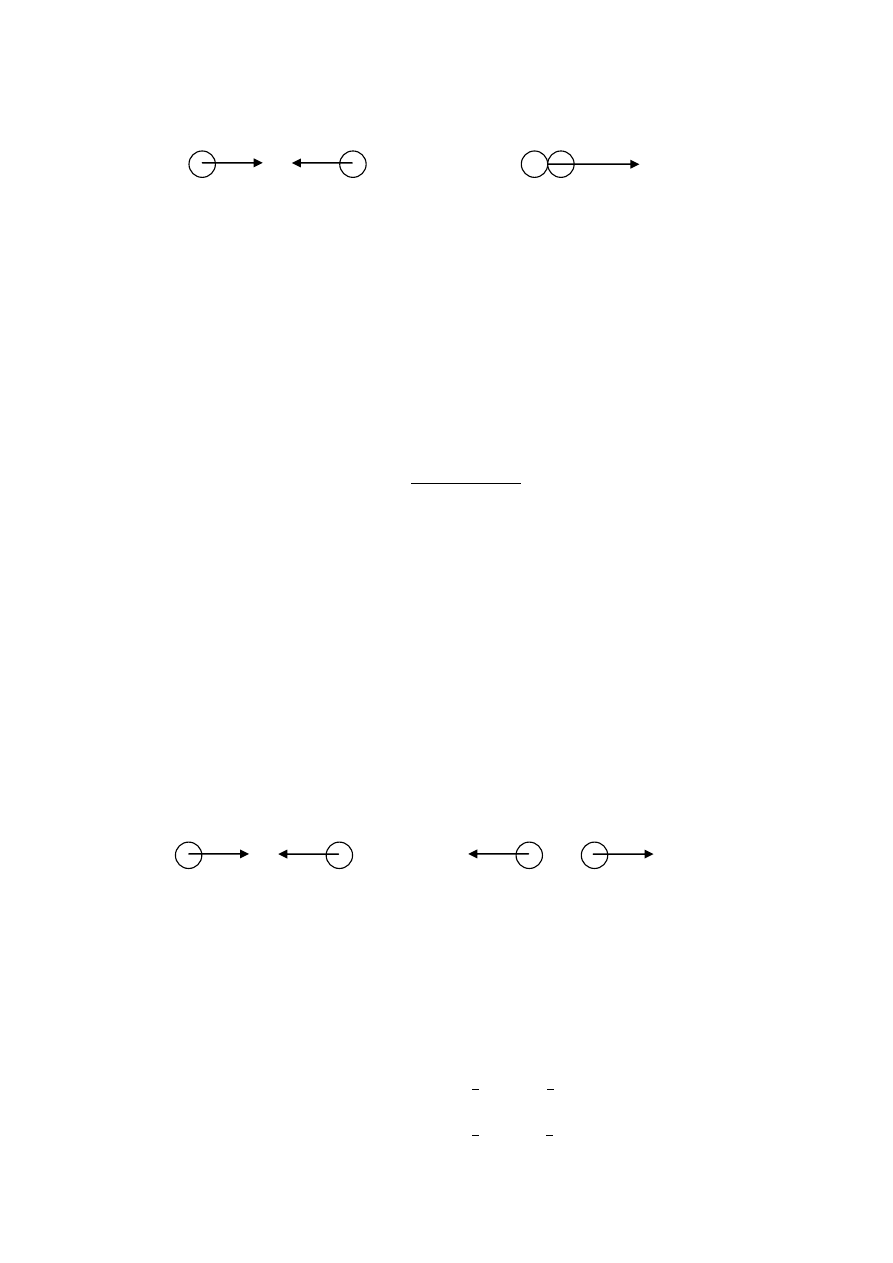
2. Dwie cząstki o masach m1, m2 i prędkościach v1, v2 zderzają się doskonale niesprężyście. Znaleźd prędkośd
cząstek po zderzeniu.

Pęd przed zderzeniem:

Pęd po zderzeniu:

Pęd jest zachowany:

Prędkośd cząstek po zderzeniu.

3. Dwie cząstki o masach m1, m2 i prędkościach v1, v2 zderzają się centralnie doskonale sprężyście. Znaleźd
prędkości cząstek po zderzeniu, a następnie rozważyd przypadek m1=m2.

Pęd przed zderzeniem:

Pęd po zderzeniu:

Pęd jest zachowany:

Energia kinetyczna przed zderzeniem:

Energia kinetyczna po zderzeniu:

Energia kinetyczna jest zachowana:

Po zderzeniu

Przed zderzeniem

Przed zderzeniem

Po zderzeniu

Otrzymujemy układ równao:

A ponieważ ruch jest jednowymiarowy wektory redukują się do skalarów (dodatnich lub ujemnych) i otrzymujemy
układ dwóch równao skalarnych:

Dla

: