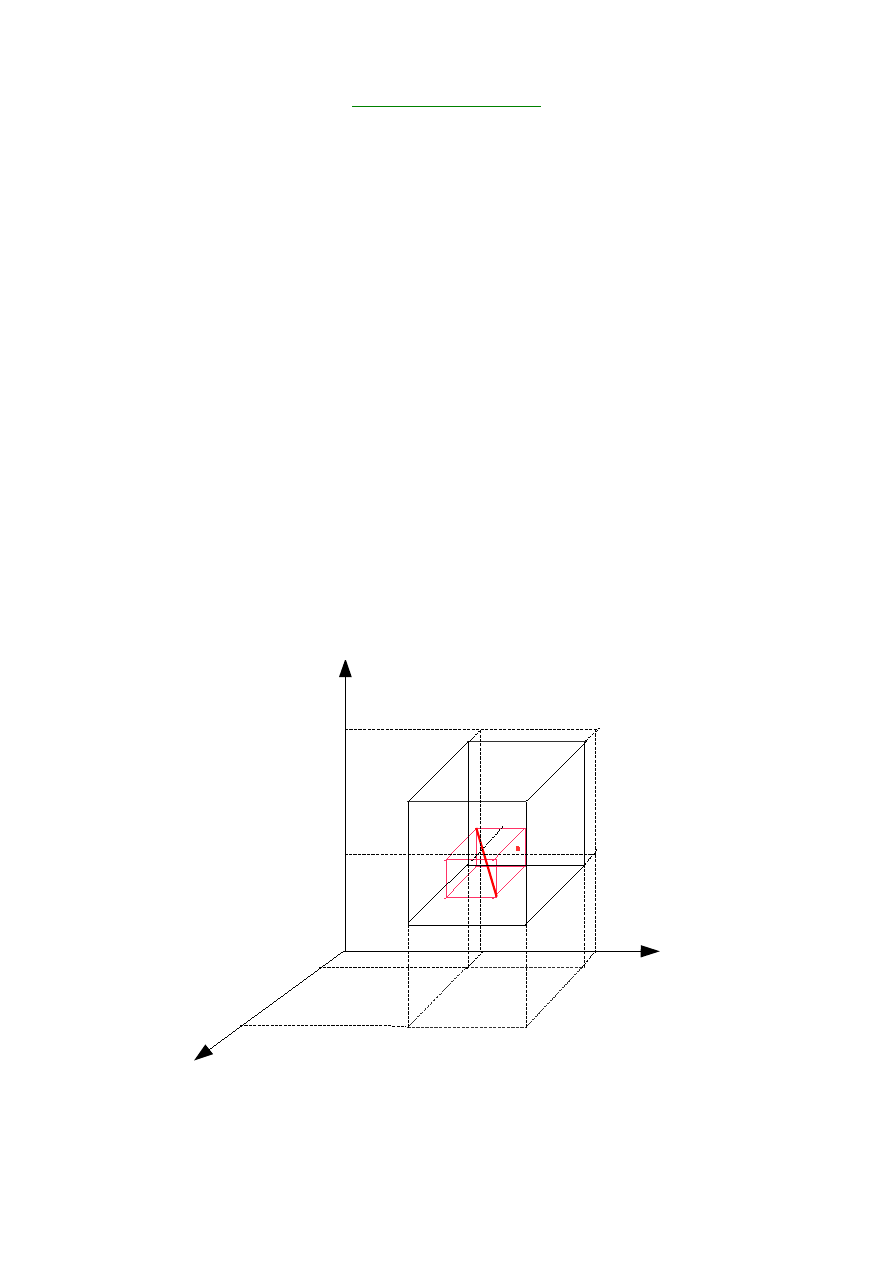
CAŁKI POTRÓJNE

Dany jest prostopadłościan P zwarty w 

oraz funkcja f,

 f – ograniczona.

Dla dowolnego           wyznaczamy podział      prostopadłościanu P
- P dzielimy na n prostopadłościanów     o objętościach         gdzie k=1,...,n
- dla k=1,...,n wyznaczamy 

długość przekątnej

     prostopadłościanu 

- wybieramy maksymalną z długości przekątnych i oznaczamy 

                                        

                        -

średnica podziału

                       

W ten sposób utworzyliśmy ciąg              podziałów prostopadłościanu P.
Następnie 
- zakładamy, że ciąg              jest ciągiem normalnym podziałów, gdzie 

                               

-

ciąg normalny podziałów

:

- dla każdego k=1,...,n wybieramy punkt                                      i tworzymy 

sumę całkową

1

 

N





n

n

N



n

k

d

k

P

,

n

























q

z

p

d

y

c

b

x

a

P :

k

n

k

n

d

,...,

1

max

:







y

x

z

b

a

c

d

P

A

k

d

k

P

k

q

p

 

N

n

n









k

k

k

k

k

k

z

y

x

A

P

A

,

,

,



.

0

lim









n

n



R



P

f :

n



 

N





n

n

,

3

R

,

n

S





k

n

k

k

k

k

n

V

z

y

x

f

S









1

,

,

:

k

P

n



,

k

V



Definicja 

(

całki potrójnej

)

Jeśli dla każdego normalnego ciągu podziałów prostopadłościanu P, ciąg sum cząstkowych  
jest zbieżny do tej samej granicy właściwej, niezależnej od wyboru punktów A

k  

, to tę granicę

nazywamy 

całką potrójną

 funkcji f w prostopadłościanie P  i oznaczamy

Uwaga 

Jeśli funkcja ograniczona f  jest ciągła poza zbiorem miary zero (

zbiór miary zero

 w R

3  

to taki zbiór,

który można pokryć skończoną liczbą prostopadłościanów, których suma objętości jest dowolnie
mała (czyli mniejsza niż ε )), to funkcja  f  jest całkowalna w prostopadłościanie P.

Interpretacja geometryczna

- objętość prostopadłościanu P.

Interpetacja fizyczna

1.               - gęstość objętościowa masy prostopadłościanu P
                                                     - masa prostopadłościanu P.

2.               - gęstość objętościowa ładunku elektrycznego prostopadłościanu P

                                                - całkowity ładunek elektryczny zgromadzony w P.

Własności całki potrójnej

Całka potrójna ma własności analogiczne jak całka podwójna (liniowość, addywność,
ograniczoność).

Twierdzenie 

(

całkowe o wartości średniej

)

Jeśli
       f – ciągła w prostopadłościanie P,
to
                                                                            -objętość prostopadłościanu P.

Twierdzenie 

(

o zamianie całki potrójnej na cąłkę iterowaną

)

Jeśli

 
to
 

oraz prawdziwe są analogiczne wzory dla pozostałych pięciu całek iterowanych.

Oznaczenia 

2

     

,

,

,

,

q

p

d

c

b

a

P







,

)

(P

C

f











  

































b

a

d

c

q

p

P

dx

dy

dz

z

y

x

f

dV

z

y

x

f

,

,

,

,









P

dV

z

y

x ,

,



 

N



n

n

S





,

,

,



P

dV

z

y

x

f





.

lim

:

,

,

0

n

P

S

dV

z

y

x

f

n













P

P

V

dV

z

y

x

f









1

,

,





z

y

x ,

,











P

dV

z

y

x ,

,









z

y

x ,

,









P

P

V

P

dV

x

y

x

f

V

c

f

P

c

 

gdzie

,

,

,

)

(

:



















dxdydz

dV

dz

z

y

x

f

dy

dx

dx

dy

dz

z

y

x

f

ozn

q

p

d

c

b

a

ozn

b

a

d

c

q

p

.

.

,

,

,

,







































  









dxdydz

z

y

x

f

dV

z

y

x

f

P

ozn

P







,

,

,

,

.

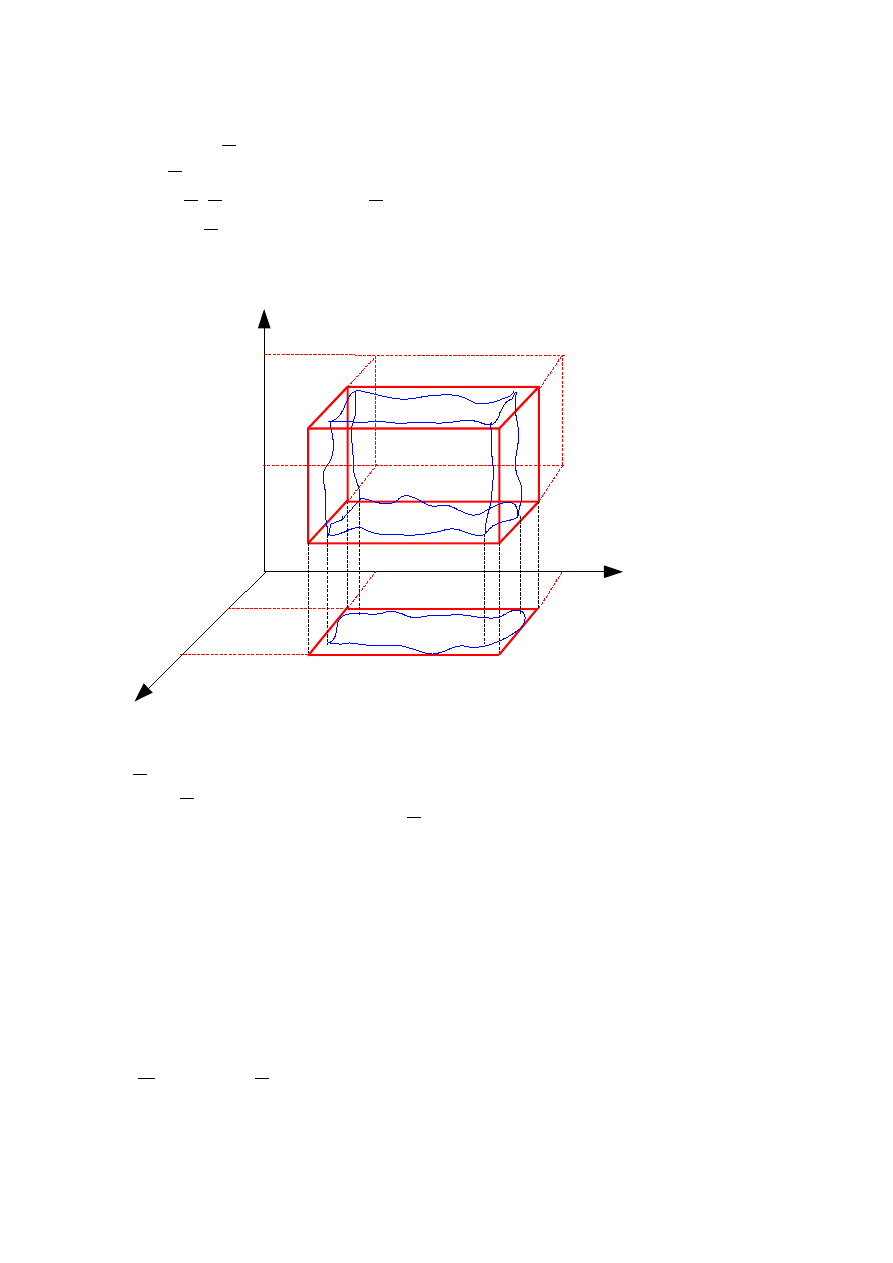
Rozszerzmy teraz definicję całki na całkę potrójna w obszarze normalnym. 

Całka potrójna po obszarze normalnym

Obszar domknięty      określony nierównościami

                            
    
 
nazywamy 

obszarem normalnym

 względem płaszczyzny OXY.

Analogicznie określamy obszar normalny względem płaszczyzny OYZ oraz względem OXZ.

Niech     -obszar normalny względem płaszczyzny OXY,

Aby wyznaczyć całkę z funkcji f w obszarze      umieszczamy ten obszar w najmniejszym
prostopadłościanie

3

y

x

z

D

a

b

c

d

p

q

z=Ψ(x,y)

z=φ(x,y)

 _
Ω

← najmniejszy      
    prostokąt          
    zawierający D

,



 

,

  

regularny,

obszar 

,

 

gdzie

OXY

D

D

D

x,y







 

D

C





,

 

.



C

f

,



     

gdzie

 ,

q

p,

,

,







d

c

b

a

P

y

d

y

c

x

b

x

a

D

D

D

D

sup

:

inf

:

sup

:

inf

:









 

 

 

 

,

,

sup

:

,

inf

:

,

,

y

x

q

y

x

p

D

y

x

D

y

x













 

.

 i

 

Zatem









C

f

P

 

 

,

,

,

:

y

x

z

y

x













Definiujemy nową funkcję:

funkcja f* jest ciągła ewentualnie poza zbiorem miary zero (może być nieciągła na powierzchniach:
z=φ(x,y), z=ψ(x,y) )
      f*-całkowalna w prostopadłościanie P.
Zatem możemy zdefiniować

                                                            całka potrójna, dla której możemy 

             zastosować tw. o zamianie całki 

                         na całkę iterowaną

i otrzymujemy wzór

Jednakże dla dowolnych (x,y) należących do rzutu       prostopadłościanu P na płaszczyznę 0XY,
 

Stąd

Podobnie prawdziwe są analogiczne wzory z całkami iterowanymi po obszarach normalnych
względem pozostałych płaszczyzn układy 0XYZ.

Wniosek

Jeśli

to

4



























dxdydz

z

y

x

f

dxdydz

z

y

x

f

P









,

,

*

:

,

,



















q

p

d

c

b

a

tw

P

dz

z

y

x

f

dy

dx

dxdydz

z

y

x

f

,

,

*

,

,

*

.

XY

P

   

mamy

,

,

d

c

b

a

P

XY













 

 

 

 























.

\

,

gdy

 

,

0

,

,

gdy

 

,

,

,

,

,

*

,

,

D

P

y

x

D

y

x

dz

z

y

x

f

dz

z

y

x

f

xy

y

x

y

x

q

p













 

 

.

,

,

,

,

,

,



 





















dxdy

dz

z

y

x

f

dxdydz

z

y

x

f

D

y

x

y

x





 

 

 

 

























y

x

z

y

x

x

y

x

b

x

a

,

,

:

















 

 

.

,

,

,

,

,

,

)

(

)

(













y

x

y

x

x

x

b

a

dz

z

y

x

f

dy

dx

dxdydz

z

y

x

f











































,

\

,

,

dla

 

0

,

,

,

dla

,

,

,

,

*

P

z

y

x

z

y

x

z

y

x

f

z

y

x

f





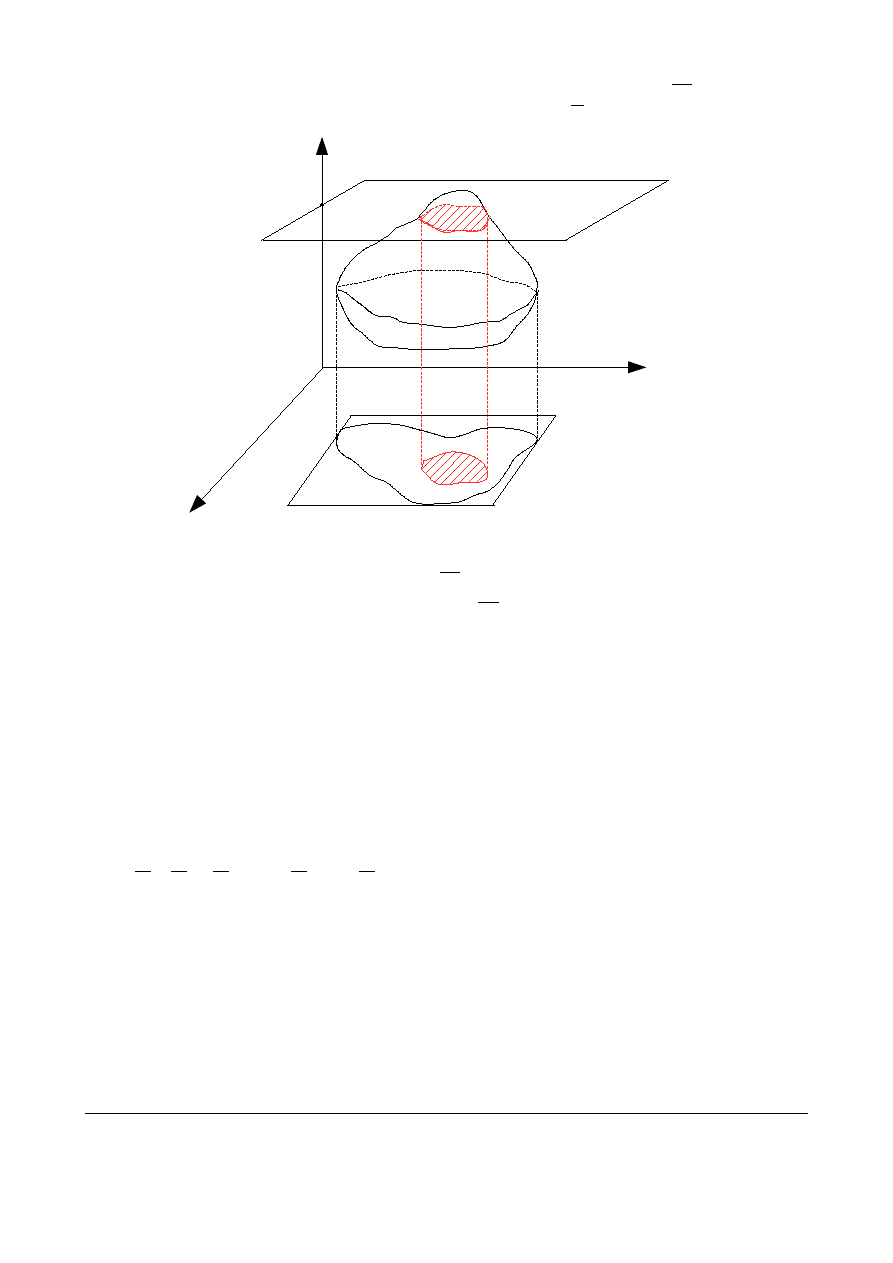
Wprowadźmy jeszcze jeden wzór na całę potrójną w obszarze normalnym.                będzie
obszarem regularnym otrzymanym z rzutowania przekroju obszaru     płaszczyzną z=const.

Wtedy dla dowolnego 

stąd

a zatem

Definicja

 (

obszaru normalnego

)

Sumę skończonej liczby obszarów normalnych względem płaszczyzn układu OXYZ o parami
rozłącznych wnętrzach nazywamy 

obszarem regularnym 

w przestrzeni.

Niech 

n

















...

2

1

, tzn. 

normalny

obszar 





i

 dla 

n

i

,

,

1 



.

          

obszar               obszary normalne o parami

                 regularny           rozłącznych wnętrzech

Wtedy definiujemy

       





















n

i

i

dxdydz

z

y

x

f

dxdydz

z

y

x

f

1

,

,

:

,

,

                                 

suma całek po obszarach normalnych

Uwaga

Całki po obszarch regularnych mają te same własności co całki po prostopadłościanach
(addywność, liniowość, ograniczoność).

opracowali Marcin Uszko i Mateusz Targosz

5



x

y

z

z=const

D

D

z

Ω

 

mamy

, q

p

z



















z

D

b

a

d

c

dxdy

z

y

x

f

dx

z

y

x

f

dy

,

,

,

,

*









.

,

,

,

,











z

D

q

p

dxdy

z

y

x

f

dz

dxdydz

z

y

x

f

XY

P









 

 















z

XY

z

D

P

y

x

D

y

x

z

y

x

f

z

y

x

f

\

,

gdy

 

,

0

,

,

gdy

,

,

,

,

,

*

z

D

Niech