1

I. PODSTAWY METODOLOGII

A. Projektowanie eksperymentów

1. Określenie problemu badawczego zakończone postawieniem poprawnej hipotezy (hipotez)
badawczych

PROBLEM BADAWCZY
- od niego rozpoczyna się badanie naukowe
- dotyczy relacji zachodzących między zmiennymi

1. Czy dana zmienna X

1

rzeczywiście wpływa na Y (X

1

jako przyczyna Y)

2. Jak dana zmienna X

1

wpływa na Y (określenie postaci związku łączącego Y z X

1

)

- związek liniowy

- związek krzywoliniowy

CECHY dobrze sformułowanego problemu badawczego:
- Pytanie lub zbiór pytań, na które odpowiedzi ma dostarczyć badanie
- Powinien sam w sobie zawierać wskazówki, co do swego rozwiązania (inaczej byłby to
pseudoproblem)
- Duża rola intuicji badawczej
- Powinien być rozstrzygalny (praktycznie)

PYTANIA ROZSTRZYGNIĘCIA I PYTANIA DOPEŁNIENIA

1. Pytania rozstrzygnięcia (większość problemów badawczych)

- zaczynają się od „czy”

- można odpowiedzieć „tak” lub „nie”

- po „czy” zdanie oznajmujące

- najczęściej formułowane są dwuczłonowe (choć istnieją pytania o różnej liczbie

członów)

- ujawniają swoje alternatywy

2. Pytania dopełnienia

- nie ujawniają alternatyw

- podają ogólny schemat odpowiedzi (funkcja zdaniowa)

- po podstawieniu odpowiednich wartości w miejsce zmiennej (zmiennych)

otrzymuje się każdorazowo nowe zdanie (prawdziwe lub fałszywe)

- zaczyna się pytaniem ogólnym „jak”, „od kiedy” itp.

UWAGI:
- należy unikać zbyt szerokiego stawiania problemu badawczego (utrudnianie rozwiązania)
- jasne zdefiniowanie pojęć wyst. w problemie – można odwołać się do już istniejących
definicji wyst. w literaturze przedmiotu
- należy zawsze odnieść się do literatury przedmiotu, by uniknąć błędów i nie badać
zbadanego już problemu


KLASYFIKACJA PYTAŃ N. BELNAPA

2

1. Czynniki determinujące typ pytania

- zbiór alternatyw (sposób prezentowania alternatyw)

- żądanie wyboru

- żądanie roszczenia zupełności (krańcowe pytania: żądanie roszcz. zupeł.

maksymalne lub minimalne)

· minimalne – 1 alternatywa

· maksymalne – wymienienie wszystkich prawdziwych alternatyw ze zbioru

2. Pytania typu „czy” i „który”
- formułując jakiekolwiek pytanie zakładamy jakieś twierdzenie (założenie pytania – w
każdym pytaniu tylko jedno, mówiące, że prawdziwa jest co najmniej 1 odpowiedź
bezpośrednia na nie)
- 6 typów pytań

PYTANIA

CZY

KTÓRY

1. O jednej alternatywie

1. O jednej alternatywie

(żądanie odpowiedzi wskazującej 1 alternatywę

- maksymalne roszczenie

prawdziwą)

zupełności

- maksymalne roszczenie zupełności

- żądanie 1 prawdziwej altern.

- żądanie 1 odp. (alternatywy)

- odpowiedz ma postać dwuczło-

- odpowiedz ma postać koniunkcji

nową (1 człon: wybór 1

alternatywy, 2 człon: stwierdzenie
prawdziwości tej alternatywy)

2. O pełnej liczbie alternatyw

2. O pełnej liczbie alternatyw

- prezentowanie alternatyw jw.

- prezentowanie alternatyw

- żądanie wyboru wszystkich prawdziwych

(wymienienie wszystkich

alternatyw

prawdziwych alternatyw)

- odp. – koniunkcja (Każde zdanie

- żądanie wyboru wszystkich

stwierdzeniem lub zaprzeczeniem kolejnej

prawdziwych alternatyw

alternatywy)

- odp. dwuczłonowa (1 człon:

koniunkcja wszystkich
prawdziwych alternatyw,
2 człon: stwierdzenie, iż
wszystkie wymienione
alternatywy są prawdziwe)

3. O nierozłącznej liczbie alternatyw

3. O nierozłącznej liczbie alternatyw

- minimalne roszczenie zupełności

- minimalne roszczenie zupełności

- żądanie wyboru: 1 z prawdziwych

- żądanie wyboru 1 z prawdziwych

alternatyw w odpowiedzi

alternatyw

- sposób prezentowania
alternatyw: podanie 1, nie
wykluczając prawdziwości
innych, niewymienionych

3

3. 3 rodzaje wad pytań
a) wady związane ze sposobem prezentowania przez pytanie alternatyw
b) wady związane z zawartym w pytaniu żądaniem wyboru
c) wady związane z żądaniem roszczenia zupełności


KLASYFIKACJA PROBLEMÓW BADAWCZYCH
1. Problemy dotyczące wartości zmiennych (pytania o przekrojowe lub dynamiczne własności
przedmiotów lub o zdarzenia i procesy, jakim te przedmioty podlegają)

- „jaką wartość przejmie dana zmienna zależna Y, gdy zmienna niezależna X
przyjmuje pewną wyróżnioną wartość m”

2. Problemy dotyczące zależności między zmiennymi

a) problemy istotnościowe)istotność zmiennych niezależnych dla innej zmiennej

zależnej)

- jakie zmienne niezależne są istotne dla zmiennej Y

- które ze zmiennych niezależnych są bardziej, a które mniej istotne dla zmiennej

zależnej Y

- czy zmienne niezależne wpływają na dana zmienną zależną, każda niezależnie od

pozostałych, czy też wchodzą ze sobą w interakcja

b) Problemy dotyczące „kształtu” zależności Y od określonej zmiennej niezależnej dla

niej istotnej

- „Jaka jest zależność zmiennej Y od zmiennej niezależnej X”

HIPOTEZA – odpowiedź na pytanie badawcze

CECHY dobrze postawionej (sformułowanej) hipotezy:
- stwierdzenie musi być sprawdzalne (empirycznie)
- muszą być powiązane związkami wynikanie ze zdaniami obserwacyjnymi
- hipotezy ad hoc – zdolne wyjaśniać tylko te fakty, do wyjaśnienia, których zostały
sformułowane (nie przewidują nowych faktów) – inaczej h. doraźna lub metodologicznie
wadliwych
- musi być adekwatną odpowiedzią na problem
- musi być najprostszą odpowiedzią na problem, im bardziej prosta przyjmie postać, tym
łatwiej będzie ja sprawdzić
- musi być tak sformułowana, by łatwo ją było przyjąć lub odrzucić
- nie powinna przyjmować postaci szerokiej generalizacji

- intersubiektywna kontrolowalność – możliwość odrzucenia hipotez innych

naukowców

4

- powinna być zawsze sformułowana w postaci twierdzącej

KLASYFIKACJA HIPOTEZ BADAWCZYCH
I. Hipotezy dot. wartości zmiennych (jeśli X przyjmuje wartość m, to Y przyjmuje wartość n)
II. Hipotezy dot. zależności między zmiennymi

1. H. istotnościowe (twierdzenia postaci)

a) X

1

, ...X

n

są istotne dla Y

b) zmienne z O(P

y

) uporządkowane są – wg. relacji bycia bardziej istotna dla Y niż

... lub „X

1

jest bardziej istotna dla Y niż X

2

)

c) X

1

, ...X

n

wpływają na zmienną zal. Y wchodząc ze sobą w interakcje

d) X

1

, ...X

n

wpływają na zmienną zal. Y nie wchodząc ze sobą w interakcje

2. H dotyczące „kształtu” zależności Y od X

Zmienną zal. Y łączy związek funkcyjny ze z. niezależna X w postaci Y=f(X)

f – określony „kształt” funkcji (f. liniowa, nieliniowa)

2. Określenie składu, liczebności i sposobu dobierania próby

PRÓBA – dowolny podzespół pobrany z populacji

Każda statystyka oblicza na podstawie pomiarów pochodzących z próby (estymator),
odpowiadającej im wartości populacyjnej (parametru populacji)
W większości populacji parametry są nieznane i muszą w pewien sposób zostać oszacowane na
podstawie danych pochodzących z próby

Większość zadań, jakimi zajmuję się statystyka polega w praktyce na wykorzystaniu statystyk z
próby jako estymatorów parametrów populacji, w szczególności zaś na określeniu wielkości
błędu, którymi estymatory te są obciążone.

Zestaw metod statystycznych służących do formułowania twierdze na temat parametrów
populacji na podstawie statystyk z próby, nazywa się STATYSTYKĄ PRÓBY; a procesy
logiczne, na których metody te się opierają określa się mianem wnioskowania statystycznego,
które jest ścisła postacią wnioskowania indukcyjnego.

Istnieją 2 różne sposoby doboru próby:

2. Badacz może sam, lub odwołując się do opinii eksperta, wybrać określone osoby do

grupy badawczej – dobór celowy (nieprobabilistyczny); jego popularną odmianą
zwłaszcza wśród socjologów jest dobór kwotowy, a także najgorszy – dobór całkowicie
przypadkowy

3. może skompletować próbę na podstawie zgłoszeń ochotników
4. może pobrać próbę z populacji w sposób losowy

Jedynie losowy dobór jednostek gwarantuje uzyskanie próby reprezentatywnej. jedynie na niej
przeprowadzone badanie empiryczne będzie cechowała wysoka trafność zewnętrzna.

5

Istnieją jednak takie sytuacje, w których z konieczności musimy stosować dobór celowy osób (w
psychologii klinicznej – badania na niewielkich grupach chorych psychicznie). Jednak trzeba być
bardzo ostrożnym w formułowaniu wniosków, które miałyby wykraczać poza tę grupę.
Odnoszenie się do opinii eksperta też nie rozwiązuje problemu (diagnozy dalekie są od
jednoznaczności i precyzji). Podobnie próba złożona z ochotników jest stronnicza gdyż w
pewnym stopniu jest tendencyjna, choćby z uwagi tego, że dobrowolnie wyraziła zgodę na udział
w badaniu.

Może najbardziej godna zaufania jest – z nielosowych sposobów budowy próby – ta, która
została utworzona techniką doboru kwotowego.
PRÓBA KWOTOWA:
Jest najbardziej rozpowszechniona wśród badaczy opinii publicznej oraz wśród psychometrów.
Aby się nią posługiwać należy znać procentowe rozkłady interesujących nas zmiennych, by
potem można je było odtworzyć w próbie. Badacz nie wyciąga do próby konkretnej wylosowanej
osoby, ale jakąś osobę, która spełnia określone kryteria przynależności do próby. Ale uzyskane
wyniki badawcze mogą być obciążone błędem, którego wielkości nie da się tak precyzyjnie jak w
przypadku prób losowych ustalić.

PRÓBA LOSOWA:
Jest to taka próba, w której każdy element populacji może się znaleźć z jednakowym
prawdopodobieństwem (def. statystyczna). Sprzyja uzyskiwaniu prób reprezentatywnych,
umożliwia też wnioskowanie o populacji na gruncie probabilistycznym.

Statystycy dzielą populacje na:

b) skończone – populacja generalna (zbiorowość statystyczna) utożsamiana ze zbiorem

pewnych rzeczywistych elementów różniących się wartością badanej cechy – w
badaniach psychologicznych, socjologicznych, pedagogicznych

c) nieskończone – zbiór nieskończony możliwych powtórzeń pewnego eksperymentu, w

którym obserwuje się wartości pewnych zmiennych. W tym sensie populacja ma status
hipotetyczny.

Istnieją 4 podstawowe podziały schematów losowania próby:

1. losowanie niezależne – losowanie zależne

Losowanie zależne (bezzwrotne, bez zwracania) – raz wylosowany element z populacji nie

jest do niej zwracany; częściej w populacjach skończonych

Losowanie niezależne (zwrotne, ze zwracaniem) – każdy wylosowany z populacji element

jest do niej zwracany; w populacjach nieskończonych

2. losowanie indywidualne – losowanie grupowe

Losowanie indywidualne – losuje się pojedyncze, nie pogrupowane elementy

Losowanie grupowe – przedmiotem losowania są pogrupowane zespoły jednostek danej

6

populacji

3. losowanie jednostopniowe – losowanie wielostopniowe

Losowanie jednostopniowe – elementy populacji losuje się z niej bezpośrednio

Losowanie wielostopniowe – zakłada kilka etapów (co najmniej 2) losowania

4. losowanie nieograniczone – losowanie ograniczone

Losowanie nieograniczone – odbywa się bezpośrednio z całej populacji (jednostopniowe)

Losowanie ograniczone – próbę kompletuje się na podstawie odrębnych losowań elementów z
poszczególnych części populacji, na które została ona uprzednio podzielona
Próby losowe dzieli się również na:
- proste – losowanie z populacji skończonych: indywidualne, nieograniczone, niezależne
- złożone – losowanie z populacji skończonych: złożone, wielostopniowe + zależne

MECHANIZMY LOSOWANIA I OPERAT LOSOWANIA:
Odpowiednim mechanizmem losowym są tablice liczb losowych. A dobry mechanizm
losowanie powinien dawać możliwość otrzymania jednoznacznej odpowiedzi czy daną jednostkę
włączyć do próby, czy nie. Powinien być nieskomplikowany i być niezależny od postępowania
eksperymentalnego.

Tablice liczb losowych – zawierają cyfry ułożone w ten sposób ze w żadnym ich następstwie nie
ma systematycznej zależności niezależnie od tego, w jakim kierunku się ją czyta, wykorzystuje
się je powszechnie przy projektowaniu eksperymentów, gdy potrzebne jest zapewnienie
kolejności losowej.

Operat losowania – ponumerowany spis wszystkich jednostek składających się na daną
populacje

Odmiany schematów losowania próby:

1. Losowanie nieograniczone indywidualne – najprostszy sposób doboru próby losowej,

mało efektywny; stosujemy, gdy populacja jest niezbyt duża, mamy o niej mało
informacji i jest jednorodna. Losowanie niezwrotne- najbardziej korzystne, musimy
dysponować rzetelnym operatem losowania; najczęściej stosuje się go w ostatnim
etapie losowania wielostopniowego

2. losowanie systematyczne indywidualne – „schemat losowania, co k-ty element”,

równie prosty, co powyższy, nie wymaga użycia tablic liczb losowych
I krok – ustalenie tzw. odstępu losowania k (liczba całkowita nieprzekraczająca
wartości ułamka k= N/n, gdzie N- elementy populacji; n – el. próby
II krok – wybór losowy liczby naturalnej N

o,

gdzie 1



N

o



k

Do próby wchodzą następujące elementy: N

o

; N

o

+k; N

o

+2k, ...

7

Ten sposób jest szczególnie wygodny, gdy dysponujemy gotowym spisem elementów
populacji; należy stosować go ostrożnie, gdy podejrzewamy występowanie
cyklicznych wahań badanej zmiennej

3. losowanie warstwowe – Stosujemy, gdy populacja wykazuje duże zróżnicowanie ze

wzg. na badaną zmienną; dzielimy całą populację na warstwy i losujemy niezależnie z
każdej warstwy określoną liczbę elementów. Podział na warstwy musi być kompletny
i rozłączny.

Dąży się do minimalizacji wariancji wewnątrzwarstwowej (zróżnicowanie pod
względem wielkości badanej zmiennej powinno być niewielkie wewnątrz warstwy) i
maksymalizacji wariancji miedzywarstwowej (duże zróżnicowanie zmiennej między
warstwami)

2 sposoby określania wielkości prób z poszczególnych warstw:

a) wariant proporcjonalny – wielkość prób losowych z warstw jest

proporcjonalna do wielkości samych warstw
n

w

=n*p

w

gdzie n

w

– próba z warstw; n – ogólna wielkość próby; p

w

–

proporcja elementów warstwy do całej populacji

b) wariant optymalny – wielkość próby z każdej warstwy proporcjonalna do

wielkości samych warstw i proporcjonalna do odchylenia
standardowego badanej zmiennej w warstwie

Opracowany przez Jerzego Spławę – Neymana w 1933

Bardziej korzystny od w. proporcjonalnego, gdy szacujemy tylko 1
parametr populacji (co w badaniach psychologicznych rzadko się
zdarza)

4. losowanie grupowe – najczęściej stosowany w praktyce (obok l. warstwowego).

Jednostkami losowania są grupy. dla populacji bardzo licznych, gdzie
brak operatu losowania.

sposób tworzenia grup jest dowolny, można jednak podać pewne
zasady:
- dążyć do maksymalizacji wariancji wewnątrz grupowej
- dążyć do minimalizacji wariancji między grupowej
- unikać czysto mechanicznego określania charakteru grup
- za grupę uznawać zespoły elementów populacji utworzonych
naturalnie (np. szkoły, gminy)

5. losowanie wielostopniowe – jest kombinacja wyżej wymienionych schematów. W

najprostszej wersji – losowanie dwustopniowe

I krok: warstwowanie populacji
II krok: losowanie niezależne z każdej warstwy określonej ilości grup

8

III krok: z każdej grupy, w ramach każdej warstwy, oddzielne losowanie zależne

pewnej liczby elementów

Do sprawdzenia czy porządek, w jakim poszczególne elementy były pobierane z populacji jest
porządkiem losowym, stosuje się test serii Walda - Wolfowitza
Test ten jest oparty na teorii serii: seria to każdy podciąg złożony z kolejnych elementów jednego
rodzaju utworzony w ciągu uporządkowanych w dowolny sposób elementów z dwu rodzajów

Wielkość próby, jaka należy pobrać z populacji zależy od tego, jakim schematem torowania
chcemy się posłużyć i jaki parametr populacji chcemy oszacować.
Pewne jest jednak, że w przypadku zastosowania wariantu bezzwrotnego do próby – potrzebna
jest mniejsza próba, niż w przypadku zastosowania wariantu zwrotnego

Błąd próby jest to różnica miedzy wartością w populacji (jej średnią), czyli parametrem, a
konkretna wartością z próby (jej średnia)

7. Określenie zmiennych

ZMIENNA – właściwość przypierająca różne wartości

PODZIAŁY:
I. Ze względu na wielkość zbioru

- dwuwartościowe (dychotomiczne) – np. płeć

- wielowartościowe (politomiczne) – np. wzrost, neurotyzm

- trójwartościowe (trychotomiczne) – np. odpowiedzi „tak”, „nie”, „nie wiem”

II.

- ciągłe – zbiór wartości tworzy kontinuum, pomiędzy dwiema sąsiadującymi

wartościami można znaleźć pośrednicząca np. wzrost

- dyskretne – brak wartości pośrednich np. typ wykształcenia, płeć

III.

- jakościowe (kategorialne) – tu należą zm. dychotomiczne i politomiczne

- ilościowe – tu należą zm. ciągłe, zm. zoperacjonalizowane za pomocą

wystandaryzowanych testów psych., zm. osobowościowe




4-5. Wybór zmiennej zależnej i niezależnej

ZMIENNA ZALEŻNA Y – jest przedmiotem badań, której związki z innymi zmiennymi badacz
określa (wyjaśnia)

ZMIENNA NIEZALEŻNA X – od zm. niezależnej zależy zm. zależna

Zm. niezależna główna X

3

to te zmienne niezależne, które oddziałują najmocniej na Y

9

Zm. niezależne uboczne X

4

6. Operacjonalizacja


Operacjonalizacja – procedura konstruowania sensu empirycznego terminów teoretycznych,
która ma umożliwić badaczowi odpowiedzi na następujące pytania:

a) do jakich aspektów świata rzeczywistego odnosi się jego problem badawczy;
b) jak bardzo wybrane przez niego wielkości i istniejące między nimi powiązania są

dostępne obserwacji;

c) w jakim zakresie wybrane przez niego obserwacje dostarczą mu informacji o wyjściowym

problemie badawczym. (wg Hornowskiej)

Inna definicja: zabieg doboru dla określonej wielkości teoretycznej jej obserwowalnych
wskaźników. Jeśli jednak zabieg ten rozumiany będzie jako bezpośrednie przełożenie wielkości
teoretycznej na język „operacji badawczych” , to operacjonalizacja może sprowadzić się do
zastępowania jednych pojęć innymi.

Z tym ujęciem procedury operacjonalizacji wiążą się nast. pojęcia:
Czynnik – pojęcie o charakterze ontologicznym, odnosi się do opisywanej przez badacza
rzeczywistości (mówi o tym jaka jest badana rzeczywistość). Definicja: rodzina klas abstrakcji od
relacji równościowej określonej w zbiorze U.

Wielkość - pojęcie o charakterze epistemologicznym (ukazujący to, w jaki sposób badacz
postrzega rzeczywistość, którą analizuje). Jest obrazem czynnika, ustalonym na gruncie
określonej wiedzy badacza (założeń akceptowanej przez niego teorii)

Zmienna - pojęcie o charakterze epistemologicznym (jw.). przyjęty przez badacza sposób
przejawiania się wielkości na poziomie obserwacji. (pojęcie utożsamione z pojęciem wskaźnika
Pawłowskiego i Nowaka)

Rozróżnienie to jest ważne dla omawianego ujęcia procedury operacjonalizacji, bo pozwala na
wyróżnienie 2 jej głównych etapów: 1) konstruowania wielkości, czyli tworzenia obrazów
czynnika teoretycznego 2) tworzenie zmiennej, czyli budowania zoperacjonalizowanego obrazu
wielkości.

Etapy procedury operacjonalizacji:

1. rekonstrukcja czynnika teoretycznego; konstrukcja wielkości
2. konceptualizacja wielkości, dobieranie wskaźników, konstruowanie zmiennej
3. dobór narzędzia pomiarowego i pomiar zmiennej

10

Operacjonalizacja – wyrażenie pojęć i terminów teoretycznych w kategoriach
operacyjnych (jednoznaczne terminy), dobór wskaźników, zbiorowości do badań –
kategorii społecznej, metod i technik, źródła badań.

Operacjonalizacja nawiązuje do idealizacyjnej teorii nauki.

7. Wybór skali pomiarowej dla każdej zmiennej

KLASYFIKACJA STEVENSA I SKALE

Nazwą skali pomiarowej określa się typ zmiennej


1) zmienne nominalne

- pozwalają na pogrupowanie obiektów wg. wartości

- można stwierdzić, że dwa obiekty są jednakowe lub różne pod względem wartości
jaką przyjmuje zmienna nominalna

- są określane mianem jakościowych

2) zmienne porządkowe

- pozwalają uporządkować obiekty wg. wartości, jakie przyjmuje zmienna porządkowa
dla X tych obiektów
- można stwierdzić, któremu z obiektów przysługuje zm. porządkowa w większym /
mniejszym stopniu
- pozwala ułożyć elementy pod względem wartości, jaką elementy przyjmują
- nie można mówić o dystansie dzielącym elementy

Dwa rodzaje uporządkowania:
a) silniejsze (całkowite): A<B<C
b) słabsze (częściowe): A



B



C

3) zmienne interwałowe (przedziałowe)

- pozwalają określić, jaka jest różnica (o ile) pod względem natężenia zmiennej
interwałowej X między dwoma elementami
- brak zera absolutnego

4) zmienne stosunkowe (ilorazowe)

- pozwalają na stwierdzenie ile razy natężenie zmiennej X dla A jest większe / mniejsze
niż dla B

- ma zero absolutne

Zmienne interwałowe i stosunkowe do zmienne ilościowe



8) Wybór sposobu manipulowania zmiennymi

11

3. Ustalenie stałej wartości zmiennej (w ten sposób ją kontrolujemy) w obu grupach

porównawczych - kontrolnej i eksperymentalnej. Czyli mierzymy np. wpływ grzanego
wina na kobiety. Dzielimy dziewczyny na pół (koniecznie losowo, czyli używając
randomizacji!) i jednej grupie dajemy grzane wino (gr. eksperymentalna), a drugiej nie
(gr. kontrolna). Obie grupy powinny być takie same przez eksperymentem, tzn. muszą
mieć takie same lub bardzo zbliżone do siebie wyniki (chodzi o średnie wyniki) pretestu.
Gdy wyniki są rozbieżne:

- eliminujemy „wredy” (ich wyniki), które zakłócają nam wyniki badania
- jeszcze raz rozlosowujemy grupy
- ograniczamy grupę badanych (jak w przypadku IQ gdy część ma 100 a cała reszta 150 –
ułomki – bey, bey)
WADY:
- mierzymy tylko część populacji, a wyniki przecież chcielibyśmy przełożyć na
wszystkich ludzi

2. „Dobieranie parami” – tworzymy dwie (albo i więcej) grupy (kontrolną i

eksperymentalną), w których jedna osoba ma swój „odpowiednik” w drugiej grupie. W
ten sposób tworzą się nam pary (gdy dwie grupy). Losowo przydzielamy jedna osobę z
pary do gr. kontrolnej a drugą do eksperymentalnej. Idealne do tego rodzaju badań są
bliźnięta jednojajowe – niestety trudno dostępne :( Gdy bliźniaków brak możemy
stworzyć parę z jednej osoby (! – możliwe tylko na metodologii :-P), czyli dwa razy
przebadać tą samą osobę. Losowo wybieramy czy dana osoba zaczyna od kontrolnych
badań, czy eksperymentalnych.

WADY:

- nie jest łatwe skonstruowanie par dla zmiennych psychologicznych

- badanie każdego człowieka i szukanie dla niego pary bardzo kosztowne

- gdy badamy osoby kilka razy mogą się wyuczyć zadań z testu

Wybór należy do Ciebie:
Jeśli możesz przeprowadzaj badania drugiego typu, ale jeśli musisz przeprowadzić badania na
większej liczbie osób i w dodatku masz kilka zmiennych nigdy nie pakuj się w badania
„dobieranie parami”



9) Randomizacja – losowe przypisanie wartości zmiennymi niezależnym (w szczególności –
podział osób między grupy eksperymentalne) – AGA ! ! !



10) Określenie zmiennych zakłócających, projektowanie sposobu eliminowania bądź
minimalizowanie ich wpływu

ZMIENNE ZAKŁÓCAJĄCE
- zmienne niezależne, które w niekontrolowany sposób wpływają na zmienną zależną
- zmienne niezależne, którymi badacz manipuluje w sposób niezamierzony

12

PODZIAŁ:
1) zmienne niejako „na zewnątrz” sytuacji badawczej, „nieskorelowane” z aktem badania
empirycznego. Są to zmienne, których oddziaływania na zmienna zależną badacz nie może
przewidzieć
np. indywidualna tolerancja osób badanych na zmiany ciśnienia atmosferycznego

2) zmienne „wewnętrzne” względem sytuacji badawczej, „skorelowane” z aktem badania
empirycznego
np. zmienne kontekstu psychologicznego badania, będące pochodna wchodzenia badacza z osobą
badaną w interakcje
- uniwersalne – występują zawsze ilekroć występują pozostałe zmienne niezależne istotne dla Y
(np. sposób odczytania wskazania przyrządu pomiarowego – pod jakim kątem patrzymy na skale)
- okazjonalne – niekiedy występują, niekiedy nie (np. zmęczenie)

Zarówno zmienne uniwersalne jak i okazjonalne mogą być kontrolowane (badacz uwzględnia ich
wpływ na zmienną zależną) lub niekontrolowane (ich wpływu badacz nie jest w stanie
uwzględnić w danym badaniu)

ELIMINOWANIE:
- randomizacja I stopnia – losowy dobór osób badanych do próby
- randomizacja II stopnia – losowy dobór osób badanych do warunków eksperymentalnych

B. Proces badawczy jako proces „wyjaśniania wariancji”

1) Rozumienie różnicy między zmiennością losową a systematyczną – MAGDA ! ! !

2) Rozumienie pojęcia wariancji – PATRYCJA ! ! !

II. STATYSTYKA OPISOWA

A. Stosowanie i interpretacja najważniejszych miar tendencji centralnej

Zacznijmy od tego, że Miary Tendencji Centralnej (dalej: MTC) (inaczej: miary

położenia) pokazują jednego, typowego reprezentanta całego zbioru (a właściwie ich celem jest
pokazanie tego reprezentanta). Taki mały cytat doktora: „Najważniejsza rzecz dotycząca
statystyki opisowej, w tym Miar Tendencji Centralnej: trzeba wiedzieć co można zrobić, co
trzeba, czego nie można i czego nie trzeba” :)


MODALNA (inaczej: moda, dominanta)

Jest to najczęstsza wartość w zbiorze

13

Jest jedyną MTC możliwą do zastosowania w przypadku danych wyrażonych na skali
nominalnej.

Stosowanie ma sens, gdy istnieją egzemplarze, które można zasadnie uznać za typowe (nie
pytajcie mnie o co chodzi – brzmi mądrze :P).

Trudno ją (jakbyś gdzieś się zgubił/a: modalną) stosować, gdy:

2. Żadna wartość nie występuje wyraźnie częściej od innych
3. Jest więcej niż jedna wartość modalna (rzadko się tak dzieje)
4. (cytat) czysty przypadek sprawia, że w danej próbie akurat ta, a nie inna z wartości

„kandydujących” do roli mody, staje się najczęstsza (koniec cytatu)

Zalety modalnej:

2. Można jej użyć zamiast średniej
3. jest jedyną MTC, która daje się użyć w przypadku zmiennych nominalnych (powtórka z

rozrywki, ale repetita madre studiorum ;) )

4. nie wymaga przyjmowania żadnych założeń odnośnie poziomu pomiaru
5. jest najbardziej zrozumiała dla laików (by Wolski TM) – ma klarowną interpretację w

języku potocznym

MEDIANA

Jest to wartość środkowa zbioru (dzieli zbiór/wykres/coś na dwie równe połowy [jakby połowy
mogłyby być nie równe])

Jest stosowana w przypadku zmiennych na skalach przedziałowych, porządkowych i
ilorazowych.

[W tym miejscu mała dygresja Wolskiego:
Zdychotomizować – podzielić na 2 części
Zdychotomizować w punkcie mediany – podzielić na 2 równe grupy]

Ograniczenia w stosowaniu:

1. Nie tyczy się zmiennych nominalnych
2. Jest bardziej podatna na fluktuacje losowe niż średnia, zwłaszcza, gdy zmienna przyjmuje

niewiele wartości (chyba że istnieje jeden „ciężki” wynik, to wtedy średnia jest bardziej
zniekształcona niż mediana)

3. Statystycy jej nie lubią ;)

Zalety:

1. Odporna na występowanie na skrajach wyjątkowo dużych lub małych wartości
2. W przypadku rozkładów skośnych pokazuje wartość typową lepiej niż średnia
3. Można ją stosować przy skrajnych przedziałach (np. 65 lat i więcej) [też nie wiem, ale

może ktoś będzie wiedział o co chodzi :P]

14

ŚREDNIA ARYTMETYCZNA

To chyba każdy wie ;)

Ograniczenia:

1. Tylko do zmiennych przedziałowych i ilorazowych
2. Wymaga symetrycznego rozkładu
3. nieodporna na skrajne wartości

Zalety:

1. najlepsza podstawa do przewidywania wartości w populacji
2. Najmniej podatna na przypadkowe fluktuacje
3. Ma szczególne własności statystyczne, np. suma odchyleń od niej = 0

INNE RZECZY NA TEMATY POKREWNE

Rozkład symetryczny: miejsce, gdzie przechodzą mediana, modalna i średnia (jeden punkt)

Rozkład asymetryczny: Mediana, moda i średnia są różne. Celem MTC jest wybranie
najlepszego kandydata. Jeśli średnia odbiega za bardzo w lewo, moda w prawo, a między nimi
jest mediana – wybieramy medianę.

B. Stosowanie i interpretacja najważniejszych miar zmienności – odchylenia
standardowego i obszaru zmienności

ROZSTĘP / ZAKRES ZMIENNOŚCI

= różnica pomiędzy najwyższym a najniższym otrzymanym wynikiem

min

max

X

X



- często w artykułach lub pracach naukowych ludzie podają po prostu wartości X

min

i X

max;

WADY:
- bardzo wrażliwa na odstające wartości.

ZALETY:
- jasna i zrozumiała dla każdego miara,
- nie wymaga obliczeń,

15

- wskazuje rzeczywiście zaobserwowane wartości;

ODCHYLENIE PRZECIĘTNE

= przeciętne odchylenie od średniej:

N

X

X

s







(wartość bezwzględna jest po to, by ominąć znaki)

N - ilość elementów w próbie

X

X



- odchylenie od średniej

X

X



- odchylenie niezależne od znaku algebraicznego

WADY:

1 rzadko jest przydatne i raczej nieużywane 
2 nie podaje się łatwo przekształceniom algebraicznym, gdyż posługujemy się w nim

wartościami bezwzględnymi (a w statystyce należy unikać wartości bezwzględnych);

ZALETY:
- łatwe w interpretacji,
- wyrażona w tych samych jednostkach co średnia;

WARIANCJA

= przeciętny kwadrat odchylenia od średniej:

Tak liczy się wariancję z populacji:





N

X

s







2

2



N- liczba elementów w populacji



- średnia w populacji





2





X

- kwadrat odchylenia od średniej

Zazwyczaj nie można zsumować wszystkich elementów z populacji i liczy się

wariancję z próby:

WARIANCJA – ESTYMATOR NIEOBCIĄŻONY





1

2

2









N

X

X

s

16

WARIANCJA – ESTYMATOR OBCIĄŻONY





N

X

X

s







2

2

X

– średnia z próby

N – liczba pomiarów w próbie

Jeżeli liczba pomiarów N jest niewielka, różnica zastosowania N i N-1 jest niewielka.

Jeśli dzielimy przez N – otrzymujemy estymator obciążony

( estymator – odnosi się do właściwości próby, w przeciwieństwie do parametru – właściwości populacji)

Jeśli dzielimy przez N-1 otrzymujemy estymator nieobciążony.

 gdybyśmy liczyli wariancje z różnych prób i je porównywali to nie powinny się one oddalać od estymatora

nieobciążonego, natomiast od obciążonego mogą się oddalać stopniowo;

WARIANCJA – ESTYMATOR NIEOBCIĄŻONY

- to najlepsza podstawa do przewidywania wariancji w

populacji. Nie używa się jej do opisu.

OGÓLNIE WARIANCJA :

- wyjaśnia zależności między zmiennymi,

- operuje jednostkami podniesionymi do kwadratu, co przeszkadza w opisie i interpretacji,

dlatego lepiej używać odchylenia standardowego 

ODCHYLENIE STANDARDOWE

= pierwiastek wariancji





N

X

s







2



w populacji





1

2









N

X

X

s

w próbie

Obydwa wzory dają taki sam wynik  drugi nie wymaga znajomości średniej

.

3 wyrażone jest w takich samych jednostkach jak średnia (nie-kwadratowych ) ,
4 dzięki niemu widoczna jest jednostka w standaryzowanym rozkładzie normalnym (na tle

pozostałych).

NIERÓWNOŚĆ CZEBYSZEWA

17

W przedziale +/- k odchyleń od średniej mieści się co najmniej:

%

100

100

2

k



obserwacji;

PRZYKŁADY Z WYKŁADU:

M +/- 2 odchyleń mieści się min 75% obserwacji : 100 – (100/4) = 100 – 25 = 75% (nie tak trudno policzyć)
M +/- 3 mieści się min 89% obserwacji
M +/- 4,4 odchyleń mieści się min 95% obserwacji
M +/- 8,1 mieści się min 99% obserwacji.

 nie stosuje się raczej w ogóle,
 nie ma też w żadnych podręcznikach,
 mamy tylko pamiętać, że coś takiego istnieje i wiedzieć mniej więcej tyle co napisałam 

PODSUMOWANIE:

Musimy pamiętać, że:
 rozstęp to różnica m. największym a najmniejszym wynikiem,
 odchylenie przeciętne jest w normalnych jednostkach i nie stosuje się go, bo używa się wartości bezwzględnych,
 wariancja jest w jednostkach kwadratowych, więc lepiej stosować odchylenie standardowe, bo jest to pierwiastek
z wariancji,
 istnieje coś takiego jak nierówność Czebyszewa...

... nio i wzory, a reszta chyba jest nieistotna 

C. Korelacja

1) Rozumienie istoty korelacji

z serii komentarze dr Wolskiego : Mierzenie korelacji jest mierzeniem podobieństwa dwu lub
więcej zmiennych; mierzenie korelacji nie jest mierzeniem zależności między zmiennymi –
wprawdzie istnienie zależności implikuje podobieństwo zmienności, ale podobieństwo
zmienności nie musi oznaczać zależności

2) Interpretacja współczynnika korelacji

Wartość współczynnika korelacji może zmieniać się między +1,0 a – 1,0
+1,0 to doskonała korelacja dodatnia -1,0 doskonała korelacja ujemna 0,0 to całkowity brak
korelacji. Korelacja dokonała w praktyce raczej nie występuje.

Dodatni współczynnik korelacji oznacza, że gdy wyniki w jednym zbiorze wzrastają to wzrastają
także wyniki w drugim zbiorze, odwrotnie w przypadku korelacji ujemnej, gdy wyniki w jednym

18

zbiorze rosną to w drugim maleją.

Im bardziej współczynnik korelacji zbliża się do wartości idealnej, tym lepiej potrafimy
przewidzieć zmiany w jednym zbiorze cech na podstawie drugiego zbioru.

ISTNIENIE KORELACJI NIE ŚWIADCZY KONIECZNIE O ZALEŻNOŚCI
PRZYCZYNOWEJ.

W wielu sytuacjach dwie zmienne są skorelowane ze sobą dlatego, że obie są skorelowane z
pewną trzecią zmienną.

Kiedy między dwoma zdarzeniami lub miarami istnieje korelacja, są one często związane tylko w
skutek zbiegu okoliczności. Np. Wędrówki wielorybów występujące co roku w czasie czyichś
urodzin.




3) Ilustracja graficzna korelacji

z serii komentarze dr Wolskiego: trzeba umieć samemu sporządzić wykres 9 nie zapominając o
opisaniu osi)

4) Dobór współczynnika korelacji, zależnie od rodzaju i ilości zmiennych

Współczynnik korelacji cząstkowej
Współczynnik ten stosujemy w celu usunięcia wpływu trzeciej zmiennej, np.:
W grupie dzieci o znacznym zróżnicowaniu wiekowym przeprowadzono badania testami inteligencji oraz testami
zdolności psychoruchowych. Zarówno inteligencja, jak i zdolności psychoruchowe rozwijają się z wiekiem.
Przeciętnie dzieci 10-letnie są bardziej inteligentne niż dzieci 6-letnie. Maja również lepiej rozwinięte zdolności
psychoruchowe. Zatem wyniki obu testów korelują ze sobą, ponieważ oba są skorelowane z wiekiem.
Dla takich danych możemy obliczyć korelację cząstkową, aby otrzymać miarę korelacji po wyeliminowaniu wpływu
wieku. Co oznacza słowo wyeliminowanie? Niech X

1

, X

2

, X

3

będą trzema zmiennymi. Korelacja między X

1

a X

2

może być wynikiem tego, że obie te zmienne są skorelowane z X

3

. Wynik w zakresie zmiennej X

1

można podzielić

na dwie części. Jedną część stanowi wynik przewidziany na podstawie X

3

. Druga część to reszta, czyli oszacowanie

błędu, jakim obciążone jest przewidywanie X

1

na podstawie X

3

. Te dwie części są od siebie niezależne, czyli nie

skorelowane ze sobą. Podobnie wynik w zakresie X

2

można podzielić na dwie części, część przewidzianą na

podstawie X

3

oraz resztę, czyli oszacowanie błędu, jakim obciążone jest przewidywanie X

1

na podstawie X

3

.

Korelację między tymi dwoma zbiorami reszt (czyli błędów oszacowania X

1

na podstawie X

3

oraz X

2

na podstawie

X

3

), stanowi współczynnik korelacji cząstkowej. Jest to część korelacji jaka pozostaje po usunięciu wpływu

trzeciej zmiennej.
Wzór na obliczenie współczynnika korelacji cząstkowej w celu usunięcia wpływu trzeciej zmiennej, ma postać:





)

1

(

)

1

(

2

23

2

13

23

13

12

3

.

12

r

r

r

r

r

r











(Zapis

3

.

12

r

oznacza korelację między resztami po usunięci wpływu X3 zarówno z X1, jak i X2.)

19

Współczynnik Pearsona
Jeśli korelacja ma charakter liniowy (w odróżnieniu od krzywoliniowego), właściwą jej miarą jest współczynnik
korelacji liniowej Pearsona (zwany też współczynnikiem korelacji według momentu iloczynowego Pearsona, albo
też krótko współczynnikiem korelacji Pearsona). Dopuszczalne jest przyjęcie założenia, że korelacja jest liniowa,
gdy obie zmienne mają rozkład normalny lub bardzo zbliżony (jednomodalny i w miarę symetryczny).

Współczynnik korelacji Pearsona przyjmuje wartości od –1 do 1. Otrzymany w wyniku obliczeń znak (dodatni lub

ujemny) informuje bezpośrednio o znaku korelacji. Korelacja dodatnia występuje wówczas, gdy zwiększaniu

wartości jednej zmiennej towarzyszy (statystycznie, a nie bezwyjątkowo) również zwiększanie wartości drugiej

zmiennej. Korelacja ujemna natomiast oznacza, że wzrostowi wartości jednej zmiennej towarzyszy spadek wartości

drugiej. Wartość bezwzględna tego współczynnika informuje natomiast o sile korelacji – im bardziej jego wartość

jest oddalona od zera (w stronę liczb –1 lub 1), tym korelacja jest silniejsza. Wzór do obliczania współczynnika

korelacji Pearsona (oznaczanego zwykle r) może zostać przedstawiony w następującej postaci:

,

gdzie:C

XY

– kowariancja między zmiennymi X i Y, natomiast S

X

oraz S

Y

– odchylenia standardowe odpowiednio

zmiennej X i Y

Współczynnik Spearmana
W sytuacji, gdy zmienne są na różnych poziomach (każda z tych zmiennych posiada inne możliwości
pomiarowe, np. zmienna Z

1

jest porządkowa, natomiast Z

2

– ilorazowa), należy wybrać procedurę

statystyczną właściwą dla zmiennej będącej na niższym poziomie. Odpowiedni jest w tej sytuacji współczynnik
korelacji rangowej Spearmana .
Współczynnik korelacji rangowej oblicza się dla pary zmiennych porządkowych (inaczej: rangowych), a więc
takich, które pozwalają jedynie porządkować badaną grupę osób ze względu na określone kryterium. Tym
samym zmienną Z

2

– ilorazową – będziemy musieli potraktować jak porządkową; abstrahując od faktycznie

uzyskanych w teście przez poszczególnych uczniów wartości punktowych, będziemy się interesować jedynie
ich kolejnością (rangą) – ma przy tym miejsce pewna utrata informacji. Współczynnik korelacji rangowej
Spearmana, podobnie jak współczynnik Pearsona, może przyjmować wartości od –1 do 1; interpretacja,
zarówno znaku, jak i bezwzględnej wartości, jest taka sama dla obu współczynników. Tak samo sprawdza się
również istotność. Wzór na obliczanie współczynnika Spearmana (oznaczanego zazwyczaj r

S

) ma postać:

,

gdzie: d

i

oznacza różnicę rang i-tej osoby – ustalanych ze względu na każdą zmienną oddzielnie.

D. Regresja liniowa prosta

1) Interpretacja prostej regresji

- pozwala na przewidywanie 1 zmiennej na podstawie znajomości drugiej zmiennej
- linia regresji jest swoistym uśrednieniem

np. dysponujemy tylko ilorazem inteligencji dziecka i chcemy przewidzieć jego wyniki w teście

20

czytania
- linia prosta określa wówczas jak przeciętne zmienia się jedna zmienna wraz ze zmianą drugiej
- opisuje ona pewna TENDENCJE charakteryzującą dane, uwzględniając wszystkie pomiary

-jeżeli wiec dysponujemy IQ dziecka i chcemy przewidzieć jego wyniki w teście czytania –
wykorzystujemy cechy tej linii

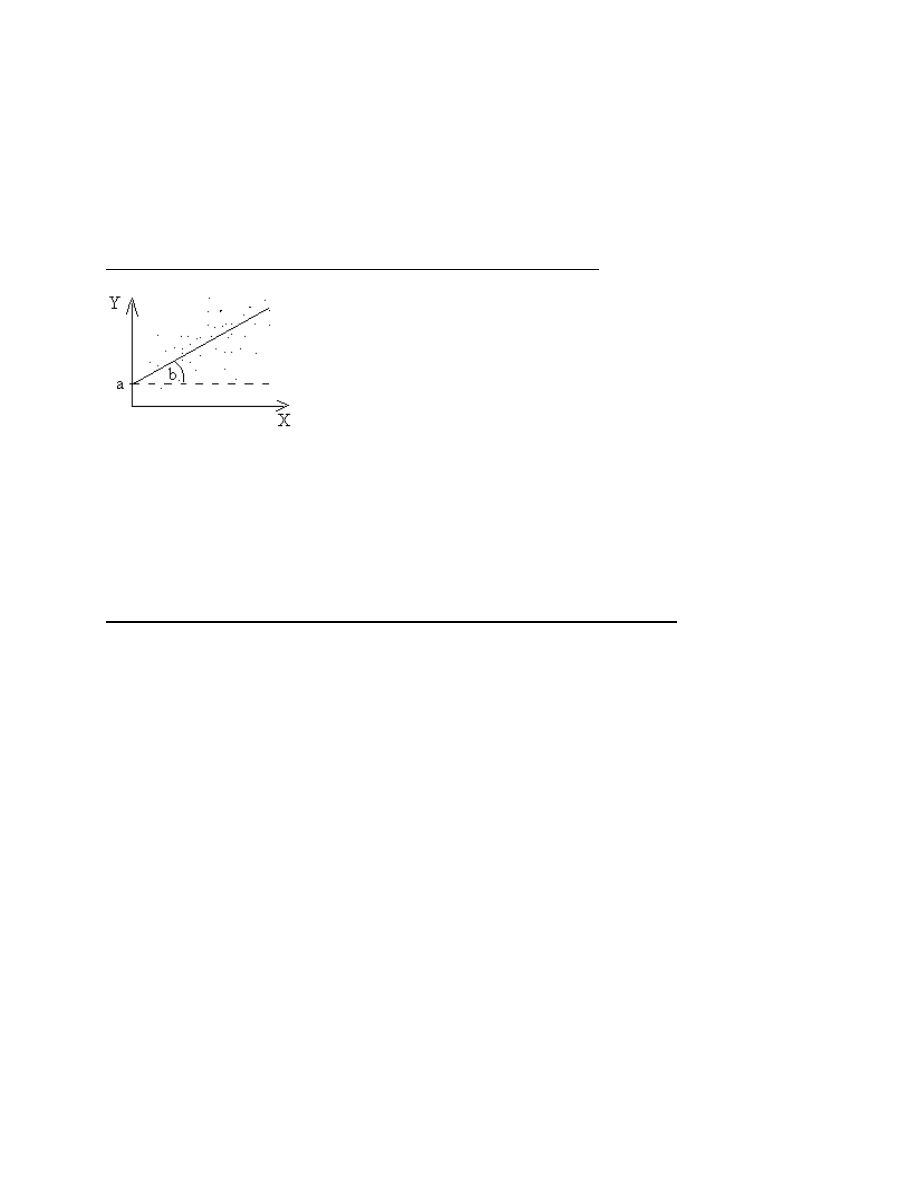
Model regresyjny pozwalający na przewidywanie Y na podstawie x:

Y= b*x+a

Y – przewidywane wyniki zmiennej zależnej
a - stała regresji, wskazuje punkt przecięcia linii regresji z osią Y
b – mówi o kącie nachylenia linii regresji względem osi X


2) Stosowanie regresji liniowej prostej do przewidywania wartości zmiennych



linia regresji jest modelem zależności, na podstawie którego można przewidywać wyniki



przyjmujemy, że odpowiednim sposobem opisu korelacji jest linia prosta, ale wcale nie musi
tak być; jeśli okazuje się, że jest inaczej, mamy do czynienia z regresją krzywoliniową, ale o
niej nawet Takane nie pisze...

(na marginesie - każdy taki wykropkowany wykres nazywa się diagramem rozproszenia)



uwaga: w psychologii praktycznie się go nie stosuje ,

ale stosowana jest regresja wieloraka (brzmi komicznie, może pan dr się pomylił, podręcznik
pisze o wielozmiennowej... w każdym razie chodzi o regresję dla więcej niż 2 zmiennych), a
liniowa to taki wstęp do niej właśnie...



zmienna, na podstawie której wyciągamy wnioski jest predyktorem



równanie regresji liniowej prostej: Y = bX + a

21



uwaga pana doktora: korelacja nie jest zależnością jednostronną, dlatego też nie ma znaczenia
co (x, y) jest podpisane pod którą osią



regresja opisuje jedynie tendencję, nie jest narzędziem do przewidywania dokładnie jak będą

się zachowywać zmienne

o czym nie powiedziano, ale Takane poświęca na to trochę czasu:



linię regresji wyznacza się metodą najmniejszych kwadratów:



regresja Y dla X:



szukamy najmniejszej sumy kwadratów odległości (w pionie - przy

standardowym podpisaniu osi) danych punktów od wyznaczanej linii („suma
kwadratów odległości” - a więc odchylenie standardowe...):



regresja X względem Y:



to samo, ale liczymy odległość w poziomie (tzn. równolegle do osi X)



zazwyczaj znajdziemy 2 linie (X dla Y i Y dla X), ale w przypadku korelacji doskonałej one
się pokryją

3) Znajomość ograniczeń metody ? ? ?

D. Rozkład zmiennych

1) Rozkład normalny – Ania ! ! !



2) Umiejętność stosowania i interpretacji skali z

Wyniki pomiarów w postaci, w jakiej zostały pierwotnie uzyskane w badaniu to WYNIKI
SUROWE. Wyniki takie oznacza się symbolem X, ich średnia dużym X z poziomą kreską na
górze, ale ponieważ cholera wie gdzie komputer ma taki symbol pozwolę sobie używać: X , a
ich odchylenie standardowe s. Odchylenia od średniej arytmetycznej, x= X-X, to wyniki
nazywane odchyleniami. Ich średnia równa jest O, a odchylenie standardowe s. Jeżeli podzielimy
odchylenia od średniej przez odchylenie standardowe, otrzymamy WYNIKI STANDARDOWE.
Oznacza się je symbolem z.

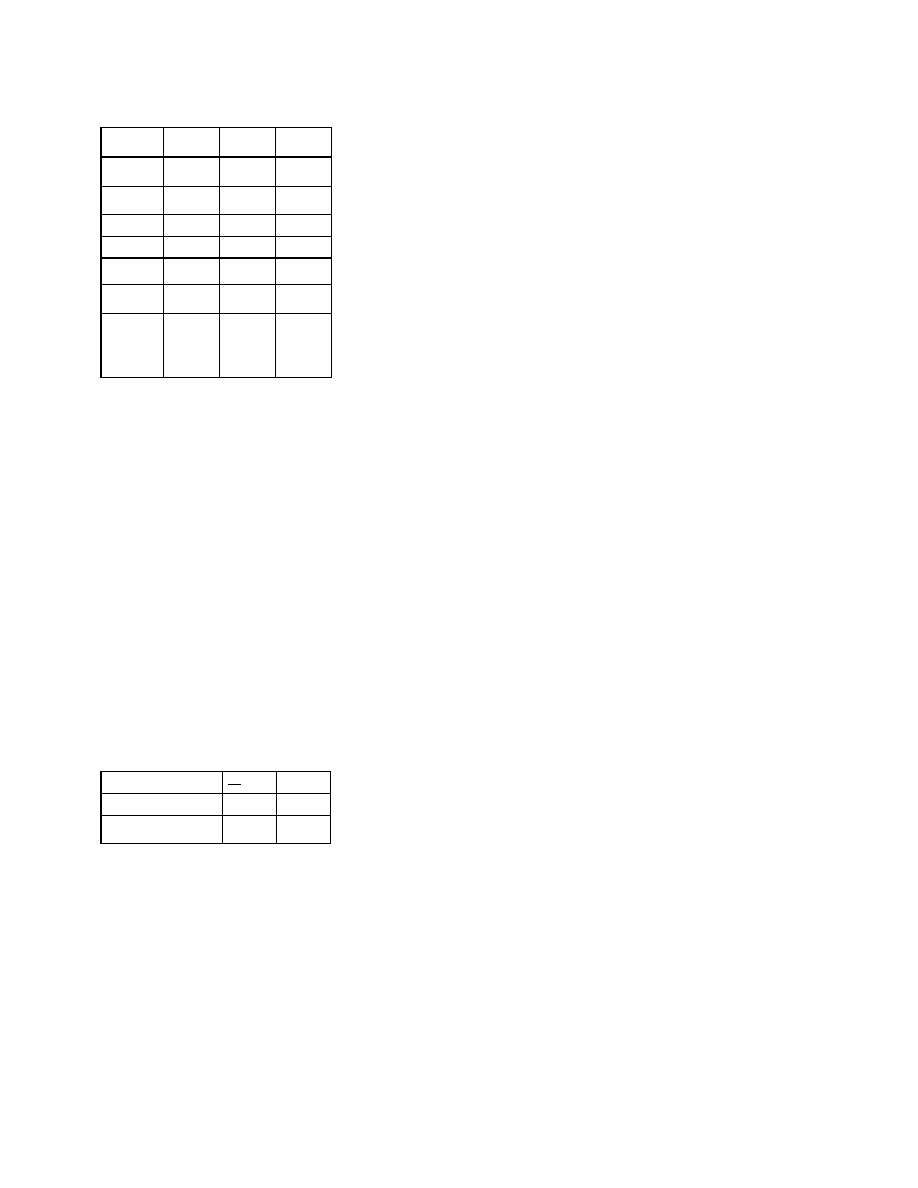
22

Osoba X

x

z

A

3

-7

-1,11

B

6

-4

-0,63

C

7

-3

-0,47

D

9

-1

-0,16

E

15

5

0,79

F

20

10

1,58

Suma
średnia
s

60
10
6,32

0,00
0,00
6,32

0,00
0,00
1,00

Wyniki standardowe maja średnią O i odchylenie standardowe 1, dzięki temu łatwo można je
poddawać przekształceniom algebraicznym. Wiele obliczeń można przeprowadzić znacznie
wygodniej, posługując się wynikami standardowymi, zamiast wynikami surowymi czy
odchyleniami.
Gdy posługujemy się wynikami standardowymi, w istocie znaczy to, ze posługujemy się
odchyleniem standardowym jako JEDNOSTKĄ POMIAROWĄ. (np. osoba A znajduje się 1,11
odchylenia standardowego 9albo jednostek odchylenia standardowego) powyżej średniej)









Wyniki standardowe często stosuje się w celu porównania pomiarów otrzymanych przy użyciu
różnych procedur. Przykład: egzaminy z j. ang. i matematyki zdane przez te sama grupę osób,
gdy średnie i odchylenia standardowe wynoszą:
egzamin

X

s

angielski

65

8

matematyka

52

12

W kontekście efektów osiąganych przez egzaminowaną grupę wynik 65 z egzaminu z
angielskiego jest równoważny wynikowi 52 z egzaminu z matematyki. Np wynik równy jednemu
odchyleniu standartowemu powyżej średniej, tzn. 52+12=64 z egzaminu z matematyki można
uważać za równoważny wynikowi równemu jednemu odchyleniu standartowemu powyżej
średniej, tzn. 65+8, czyli 73 z egzaminu z angielskiego. Jeżeli pewna osoba uzyskała wynik 57 z
egzaminu z angielskiego i wynik 58 z egzaminu z matematyki, możemy porównać między sobą
jej względne efekty egzaminów z tych dwóch przedmiotów, porównując jej wyniki standardowe.
Z angielskiego jej wynik standardowy wynosi (57-65)/8=-1,0, a z matematyki zaś o 0,5 jednostki
odchylenia standardowego powyżej przeciętnej. Widać wiec wyraźnie, że osoba ta jest znacznie
słabsza w ang. niż z matem. W kontekście efektów osiąganych przez grupę zdającą egzaminy,

23

choć nie odzwierciedlają tego oceny pierwotne.

Obszary pod krzywą normalną





Obszar pod krzywa między rzędnymi poprowadzonymi w punktach z=0 i z=1 stanowi 0,3413
całości. A zatem w przybliżeniu 34% całego obszaru mieści się między średnia a jedną jednostką
odchylenia standardowego powyżej średniej. (Dalej – miedzy z=0 i z=2, 0,4772, a zatem ok.
47.7% itd.)

Krzywa jest symetryczna, więc obszar miedzy z=0 i z=-1 również wynosi 0,3413, itd.
Część obszaru zawartego w granicach z=



1 równa jest: 0,3413+0,3413, czyli ok. 68,3%

z=



3: 0,49865+0,49865=0,99730, ok. 99,7%

Obszar pozostający poza tymi granicami jest b. mały i stanowi tylko (0,27), czyli ok. 0,3%
całości obszaru. Ze względów praktycznych przyjmuje się czasem, że krzywa rozciąga się
między z=



3.

Część obszaru poniżej średniej wynosi 0,5000. Część całego obszaru poniżej z=1 równa jest
0,5000+0,3413=0,8413. Część obszaru leżąca powyżej tego punktu wynosi 1,000-
0,8413=0,1587. W ten sposób określa się część obszaru leżącą powyżej lub poniżej dowolnego
punktu na linii podstawowej.

WYKŁAD:
- porównując rozkłady musimy uwzględnić: zależność od średniej i zależność od rozproszenia
- punkt zerowy w skali z to średnia
- jednostka to odchylenie standardowe
- ustalanie wyniku z- standaryzowanie
- 95% obserwacji mieści się w obszarze X



1,96 z

99% obserwacji mieści się w obszarze X



2,58 z

95% obserwacji mieści się w obszarze od minus nieskończoności do + 1,64 z
99% obserwacji mieści się w obszarze od minus nieskończoności do + 2,33 z



3) Znajomość właściwości rozkładu normalnego

6. Krzywa jest symetryczna. Średnia, mediana i wartość modalna zbiegają się w jednym

punkcie. Czyli: Wykres rozkładu normalnego jest symetryczny, to znaczy, że jest odbity
lustrzanie względem środka wykresu, który tutaj jest jednocześnie najwyższą wartością
funkcji (przyjmuje najwyższą wartość na osi Y), inaczej mówiąc wygląda jak górka z

24

dwoma identycznymi zboczami. Średnia, mediana (wartość środkowa) i wartość modalna
(wartość najczęstsza), występują w tym samym punkcie na wykresie, który jest
jednocześnie środkiem wykresu.

7. Najwyższa rzędna krzywej występuje w punkcie średniej, czyli gdy z = 0, i w

jednostkowej krzywej normalnej równa jest 0,3989. Czyli: tak jak już wspomniałem
najwyższa rzędna krzywej, to jest największa wartość jaką przyjmuje wykres na osi Y, na
osi X zaś przyjmuje wartość z=0, albo 0,3989.

8. Krzywa jest asymptotyczna. Zbliża się ona do osi poziomej, lecz nigdy do niej nie

dochodzi i rozciąga się od minus nieskończoności do plus nieskończoności. Czyli po
prostu nasza górka w prawo jak i lewa cały czas „schodzi” w dół jednakże nigdy nie
dotrze do osi X, zatem „schodzi” w dół coraz wolniej, ale w nieskończoność.

9. Punkty zagięcia krzywej znajdują się w miejscach plus, lub minus jedną jednostkę

odchylenia standardowego powyżej i poniżej średniej. W tych więc miejscach krzywa
zmienia się względem osi poziomej z wypukłej we wklęsłą. Czyli: W miejscach gdzie
wykres na osi X przyjmuje wartość z=1, lub z=-1, występują punkty przegięcia, w których
wykres zmienia się z wypukłego we wklęsły (najprościej to sobie wyobrazić, że wykres
wypukły przypomina smutną mine

, a wklęsły wesołą ). Najprawdopodobniej

właściwości matematyczne wklęsłego lub wypukłego wykresu nie są nam potrzebne, więc
trzeba tylko wiedzieć, że coś takiego jest i gdzie są punkty przegięcia.

10. Mniej więcej 68 % powierzchni pod krzywą mieści się w granicach plus lub minus jednej

jednostki odchylenia standardowego od średniej. Czyli: Powierzchnia pod wykresem
ograniczona wartościami na osi X równymi z=1 i z =-1, wynosi mniej więcej 68 %
całej powierzchni pod wykresem. Zatem wokół wartości średniej skupia się najwięcej
wartości.

11. W jednostkowej krzywej normalnej granice z=+-1,96 obejmują 95 procent, a granice z=+-

2,58 obejmują 99 procent całkowitej powierzchni pod krzywą, przy czym odpowiednio 5
procent i 1 procetn powierzchni mieści się po za tymi granicami. Czyli: Powierzchnia pod
wykresem ograniczona wartościami na osi X równymi z=+-1,96 wynosi mniej więcej 95%
powierzchni całkowitej pod wykresem i odpowiednio ograniczona wartościami na osi X
równymi z=+-2,58 wynosi mniej więcej 99 % całkowitej powierzchni pod wykresem. To
prawie na 100% będzie na egzaminie, więc powinno się mieć możliwość przywołania
tych wartości podczas egzaminu!

12. Model nie przesądza o najwyższej ani najniższej wartości, czyli nie można na jego

podstawie o tych wartościach wyrokować

13. Wokół wartości średniej skupia się najwięcej wartości.
14. Rozkład jest pewnym szczególnym przypadkiem rozkładu prawdopodobieństwa.
15. Centralne stwierdzenie graniczne – rozkład ze średniej prób jest zawsze rozkładem

normalnym.

16. Przy małych liczebnościach stosuje się test T studenta, im większa próba, tym wykres

wyników tego testu jest wyżej od osi X.

4) sporządzanie i interpretacja histogramu

5) Porównywanie rozkładu empirycznego zmiennej z krzywą rozkładu normalnego przy użyciu

25

testu chi-kwadrat (χ

2

)

DEFINICJA:
Miara określająca rozbieżność między zaobserwowanymi i oczekiwanymi liczebnościami.

χ2=



O – liczebność zaobserwowana
E – liczebność oczekiwana (teoretyczna)



- im większa rozbieżność tym większe χ

2

- χ

2

zawsze nieujemne

STOPNIE SWOBODY (związane z wartością χ

2

)

ilość liczebności które mogą się swobodnie zmieniać (pozostałe są określane przez te zmieniające
się)
np. przy kilkukrotnym rzucie monetą - ilość wyrzuconych orłów określa ilość wyrzuconych
reszek i odwrotnie, tzn. jeśli wiemy że w 100 rzutach wyrzucono 56 orłów wiemy że wyrzucono
44 reszki – tylko jedna liczebność może się zmieniać dowolnie a wiec JEDEN STOPIEŃ
SWOBODY
przy rzutach kostką, dopiero kiedy wiemy ile razy wypadło 1, 2, 3, 4, 5 możemy określić ile
wypadło 6 a wiec PIĘĆ STOPNI SWOBODY

Dla każdego stopnia swobody (df) istnieje inny rozkład χ

2

.

Sposób porównywania rozkładu empirycznego zmiennej z krzywą rozkładu normalnego:

I. Zakładamy hipotezę zerową: Miedzy liczebnościami zaobserwowanymi a oczekiwanymi nie
ma żadnej różnicy.
II. Obliczamy wartość χ

2

III. Porównujemy uzyskaną wartość χ2 z wartościa krytyczną wymaganą dla istotności przy
odpowiedniej liczbie df (wartości krytyczne znajdują się w tablicach uczenie ich chyba mija się z
celem ;) )
IV. Jeśli wartość uzyskana jest równa lub wyższa od odpowiedniej wartości krytyczniej to
hipotezę zerową odrzucamy. Możemy wówczas twierdzić, że różnice między liczebnościami
zaobserwowanymi a oczekiwanymi są istotne i nie można ich wyjaśnić wahaniami związanymi z
pobieraniem prób.

6) przy użyciu testu Kołmogorowa – Smirnowa

7) interpretacja miar asymetrii (skośności) i spłaszczenia (kurtozy) KRZYSIU ! ! !

8) Rozumienie konsekwencji niezgodności rozkładu empirycznego z krzywą rozkładu normalnego

z serii komentarze dr Wolskiego : Chodzi o konsekwencje dotyczące wnioskowania

26

statystycznego, konkretniej możliwości stosowania określonych technik statystycznych; wymaga
rozumienia rozróżnienia między metodami parametrycznymi i metodami nieparametrycznymi.
Warto też wiedzieć, że zmienne o rozkładzie odbiegającym od normalnego można często poddać
odpowiedniej transformacji, w efekcie której rozkład uzyska pożądany kształt zgodny z krzywą
Gaussa. Takim zabiegiem jest np. przekształcenie czasów reakcji prostej w ich logarytmy
dziesiętne.