
Egzamin dla Aktuariuszy z 24 listopada 1997 r.
Prawdopodobieństwo i Statystyka
Zadanie 1
2
6
- wybór cyfr
3 – pozycja cyfry pojedynczej
2 – albo 2x jedna albo 1x
36
15
36
5
3
6
!
4
2
!
5
2
3
6
2
3
2
6
2
3
=
⋅
=
⋅
⋅
⋅
⋅
=
⋅
⋅
=
ODP
Zadanie 2
(
)
(
) ( )
∑
=
=
5
1
II
c
i
III
II
w
c
III
z
c
i
i
P
c
P
P
( ) ( )
11
1
11
4
4
1
1
4
3
2
1
4
1
4
1
5
1
5
1
4
1
II)
w
(
)
1
(
1
II
II
c
1
=
=
+
+
+
+
=
=
c
P
P
c
P
P
( )
11
1
11
4
4
1
II
c
2
=
=
P
analogicznie
( )
11
2
11
4
2
1
II
c
3
=
=
P
( )
11
3
11
4
4
3
II
c
4
=
=
P
( )
11
4
II
c
5
=
P
33
20
3
20
11
1
4
2
3
2
11
1
11
4
11
3
3
2
11
2
3
1
=
=
+
+
=
+
+
=
ODP
Zadanie 3
Z teorii założenie że (B) obejmuje (A) bo w przypadku zdegenerowanego też
Czyli prawidłowa odpowiedź (B)
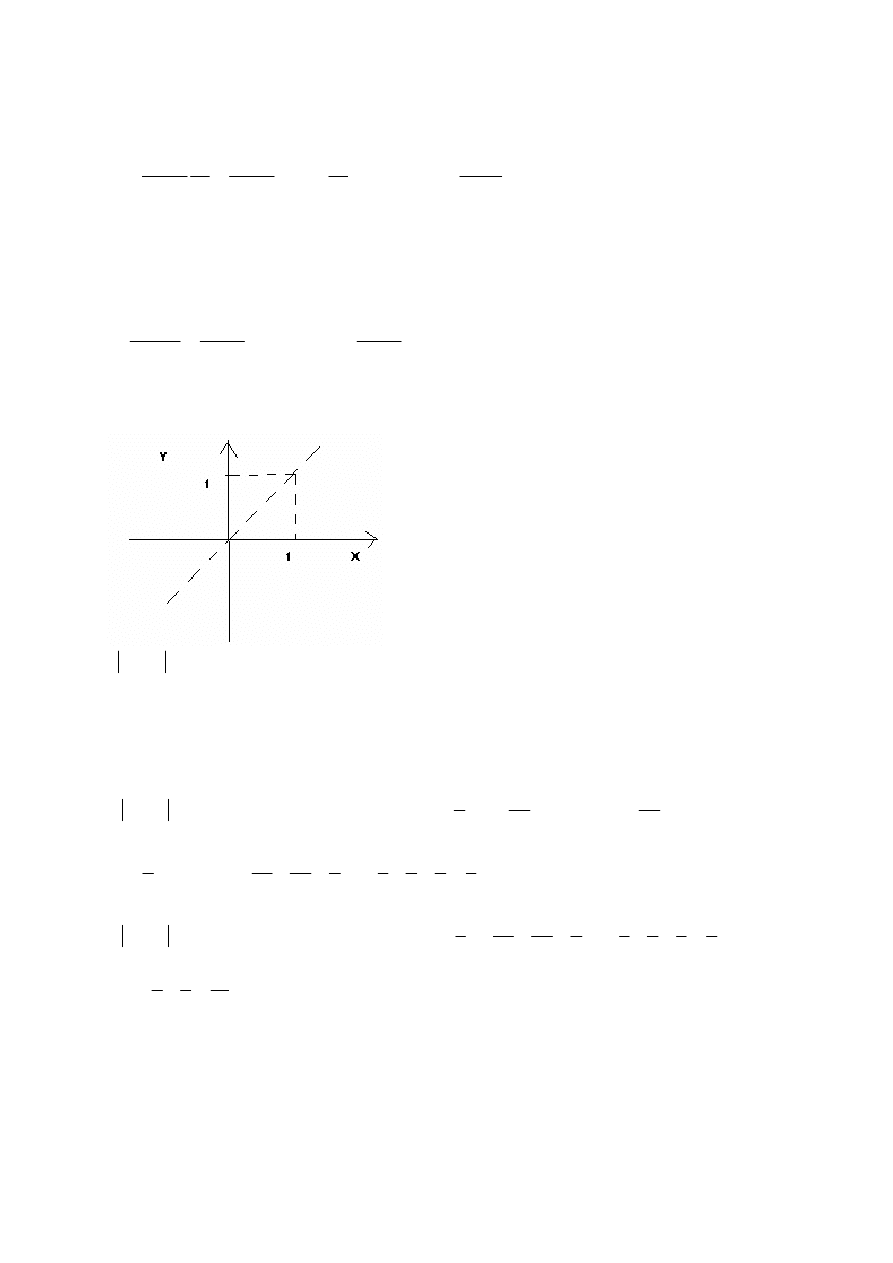
Zadanie 4
(
)
∑
∑
∞
=
∞
=
−
−
−
=
−
−
=
−
−
1
1
0
0
0
1
1
!
1
1
!
1
1
k
k
λ
λ
λ
k
λ
λ
k
λ
e
e
p
λ
e
k
λ
k
e
e
p
k
λ
e
p
k
Zadanie 5
99
,
0
)
(
20
=
a
F
F(a)=0,99949
329
,
10
)
92
,
3
;
87
,
3
(
1
,
0
10
99949
,
0
1
,
0
10
1
,
0
10
≈
→
∈
−
→
=
−
≤
−
a
a
a
X
P
Zadanie 6
≤
>
−
y
-
x x
y
dla
x
-
y
x
y
dla
Y
X
∫ ∫
∫ ∫
∫
∫
=
−
+
+
−
−
=
−
+
−
=
−
1
0
1
1
0 0
1
0
1
0
2
2
2
2
2
2
2
1
)
(
)
(
x
x
x
x
x
x
x
dydx
y
x
dydx
x
y
Y
X
E
∫
=
+
−
=
+
−
=
+
−
=
1
0
1
0
2
3
2
3
1
2
1
2
1
3
1
2
2
3
2
1
x
x
x
x
x
(
)
∫ ∫
∫
=
+
−
=
+
−
=
+
−
=
+
−
=
−
1
0
1
0
1
0
1
0
2
3
2
2
2
2
6
1
3
1
2
1
3
1
3
2
3
3
1
2
x
x
x
x
x
dydx
y
xy
x
Y
X
E
18
1
9
1
6
1
var
=
−
=
Zadanie 7
[
] [
]
2
1
1
0
2
1
0
2
)
1
(
)
1
)(
1
(
)
1
(
n
n
n
n
n
n
n
θ
θ
θ
θ
θ
θ
θ
L
+
+
−
=
−
−
−
=
(
)
(
)
)
1
ln(
2
ln
ln
2
1
1
0
θ
n
n
θ
n
n
L
−
+
+
+
=
(
)
(
)
0
)
1
(
2
)
1
(
1
2
2
1
1
0
2
1
1
0
=
−
+
−
−
+
=
−
+
−
+
=
∂
∂
θ
θ
θ
n
n
θ
n
n
θ
n
n
θ
n
n
θ
(
)
1
0
2
1
1
0
2
n
n
n
n
θ
n
n
+
+
+
=
+
2
1
1
0
0
2
1
1
0
2
2
ˆ
n
n
n
n
n
n
n
n
n
n
θ
+
+
+
=
+
+
+
=
Zadanie 8
Wiemy, że
X
S
i
2
niezależne zmienne losowe
≅
n
σ
µ
N
X
2
;
( )
(
)
( )
(
)
( )
(
)
=
>
≥
+
<
=
α
α
α
t
µ
t
P
t
µ
t
X
E
t
µ
t
P
µ
µ
E
0
0
0
0
~
( )
(
)
( )
(
)
=
<
<
−
+
=
α
α
t
µ
t
P
t
µ
t
X
E
µ
P
µ
0
0
0
(...)
(
) ( )
( )
∫
∫
+
+
−
=
−
+
=
2
2
0
0
2
..
2
0
S
S
t
µ
µ
S
t
α
α
S
f
X
f
X
µ
µ
można zbadać monotoniczność
( )
µ
C
µ
B
X
f
A
=
=
=
,
,
0
→
=
0
.
µ
µ
I
nieobciąż.
( )
( )
∫ ∫
−
>
→
>
→
+
→
>
2
2
...
...
2
2
2
0
0
~
0
dla
min
.
S
S
t
α
α
µ
µ
E
S
f
X
f
S
t
S
t
µ
X
µ
µ
II
X
µ
µ
III
→
<
0
.
odwrotnie w każdym razie odpowiedź (E) jest prawidłowa
Zadanie 9
20
ln
05
,
0
)
(
0
=
=
=
>
−
=
t
e
t
X
P
t
θ
dla
20
ln
≥
θ
moc=1 OK.
dla
20
ln
<
θ
∫
∞
−
−
−
−
−
+
≥
→
≥
=
20
ln
)
20
(ln
)
(
10
ln
9
ln
20
ln
9
,
0
θ
e
e
θ
θ
x
Razem:
[
)
∞
+
−
;
9
ln
10
ln
20
ln

Zadanie 10
Tu błąd : powinno być
i
i
i
Y
X
R
−
=
Założenie, że:
0
p
p
=
Wtedy:
2
0
2
2
0
2
2
2
var
2
2
var
2
0
σ
σ
σ
σ
µ
p
R
p
Z
EZ
ER
i
i
i
i
−
=
+
=
=
=
)
1
(
2
2
)
1
(
)
1
(
2
2
)
1
(
2
0
2
2
2
0
2
2
−
≅
−
−
−
≅
+
−
n
χ
σ
p
σ
n
S
n
χ
σ
p
σ
n
S
R
Z
→
nzl.
Y
X
Y
-
X
)
1
;
1
(
1
1
2
2
0
0
+
−
−
≅
+
−
bo
n
n
F
S
S
p
p
R
Z
Wyszukiwarka
Podobne podstrony:
2001 03 24 prawdopodobie stwo i statystykaid 21605
1997.06.21 prawdopodobie stwo i statystyka
1996.11.16 prawdopodobie stwo i statystyka
1997.04.05 prawdopodobie stwo i statystyka
1997.01.18 prawdopodobie stwo i statystyka
2001.03.24 prawdopodobie stwo i statystyka
1996 11 16 prawdopodobie stwo i statystykaid 18573
2001 03 24 prawdopodobie stwo i statystykaid 21605
1997 06 21 prawdopodobie stwo i statystyka
1997 04 05 prawdopodobie stwo i statystyka
1997 01 18 prawdopodobie stwo i statystyka
2004 10 11 prawdopodobie stwo i statystykaid 25166
2004.10.11 prawdopodobie stwo i statystyka
2003.10.11 prawdopodobie stwo i statystyka
2003 10 11 prawdopodobie stwo i statystykaid 21705
2004 10 11 prawdopodobie stwo i statystykaid 25166
więcej podobnych podstron