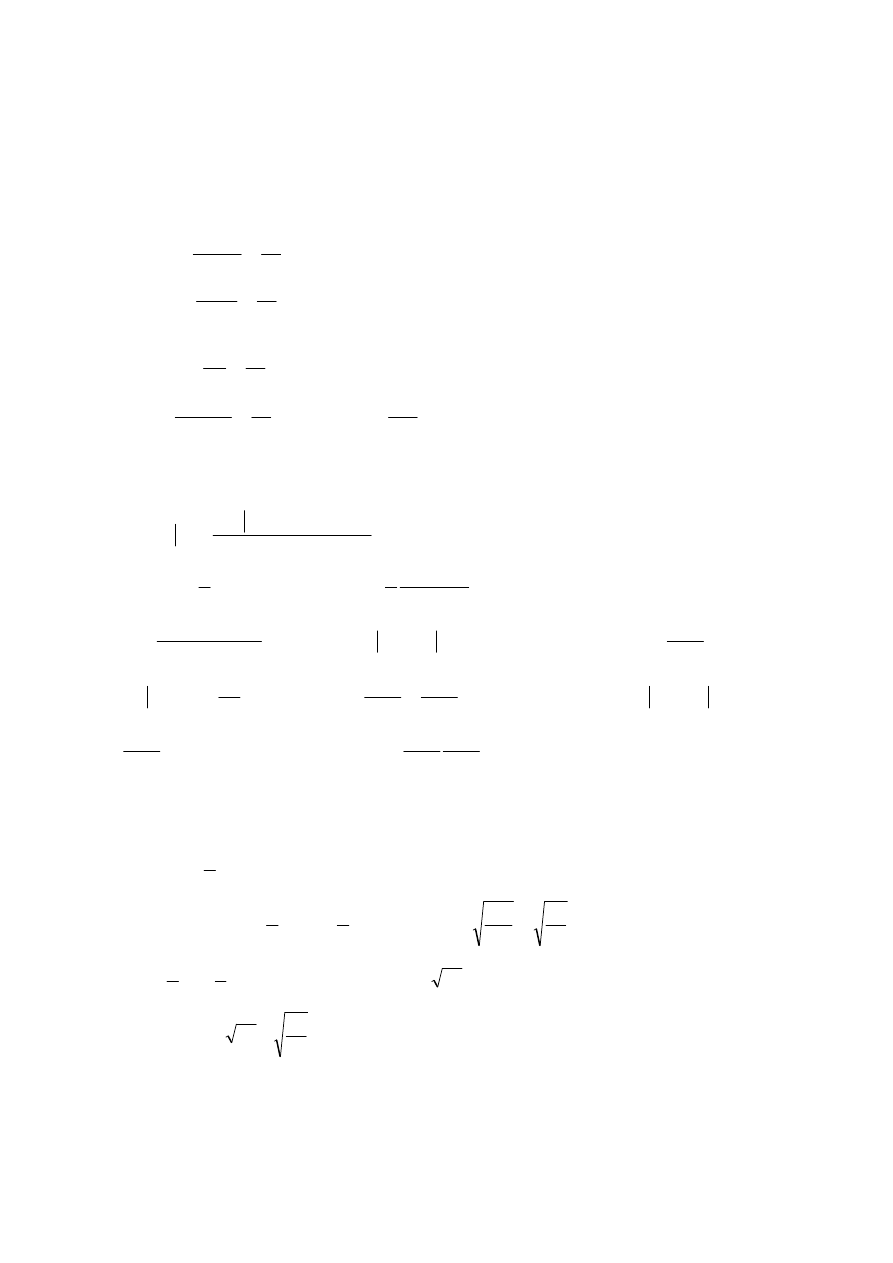
Egzamin dla Aktuariuszy z 11 października 2003 r.
Prawdopodobieństwo i Statystyka
Zadanie 1
55
10
!
55
!
54
10
)
1
(
=
⋅
=
=
X
P
55
9
!
55
!
54
9
)
2
(
=
⋅
=
=
X
P
.......
55
1
!
55
!
54
)
10
(
=
=
=
X
P
(
)
∑
=
=
=
−
⋅
=
−
=
10
1
4
55
220
385
55
11
55
1
55
)
11
(
i
i
i
EX
Zadanie 2
(
) (
)
(
)
)
(
A
P
k
S
P
k
S
A
P
A
k
S
P
n
n
n
=
=
=
=
∑
∑
=
=
−
−
=
−
−
=
−
=
n
k
n
k
k
n
k
k
n
k
p
p
k
n
k
n
n
k
a
p
p
k
n
n
k
a
A
P
0
1
)
1
(
)!
(
!
!
)
1
(
)
(
∑
∑
=
−
=
−
−
+
−
−
=
−
−
=
=
−
=
−
−
−
−
=
n
k
n
l
l
n
l
k
n
k
p
ap
p
p
l
n
a
l
k
p
p
k
n
k
n
a
1
1
0
1
1
1
)
1
(
1
1
)
1
(
)!
(
)!
1
(
)!
1
(
( )
∑
∑
=
=
−
−
=
=
−
=
−
−
−
−
=
−
−
=
n
k
n
k
k
n
k
k
n
k
n
l
k
p
kp
k
n
p
p
ap
p
p
p
k
n
n
k
a
A
S
E
0
1
2
1
)
1
(
1
1
1
1
)
1
(
(
)
∑
−
=
−
−
+
+
−
=
+
−
−
−
=
−
+
−
−
=
1
0
1
1
1
1
)
1
(
1
1
)
1
(
)
1
(
1
1
n
l
l
n
l
p
np
p
n
p
p
p
p
p
p
l
l
n
p
p
Zadanie 3
n
θ
t
t
M
P
=
≤
)
(
n
n
n
a
a
a
θ
M
P
aM
θ
P
19
20
95
100
05
,
0
1
1
)
(
=
=
→
=
−
=
>
=
<
n
n
n
b
b
b
b
θ
M
P
20
20
05
,
0
1
=
→
=
→
=
=
<
−
=
−
n
n
M
aM
bM
19
20
20
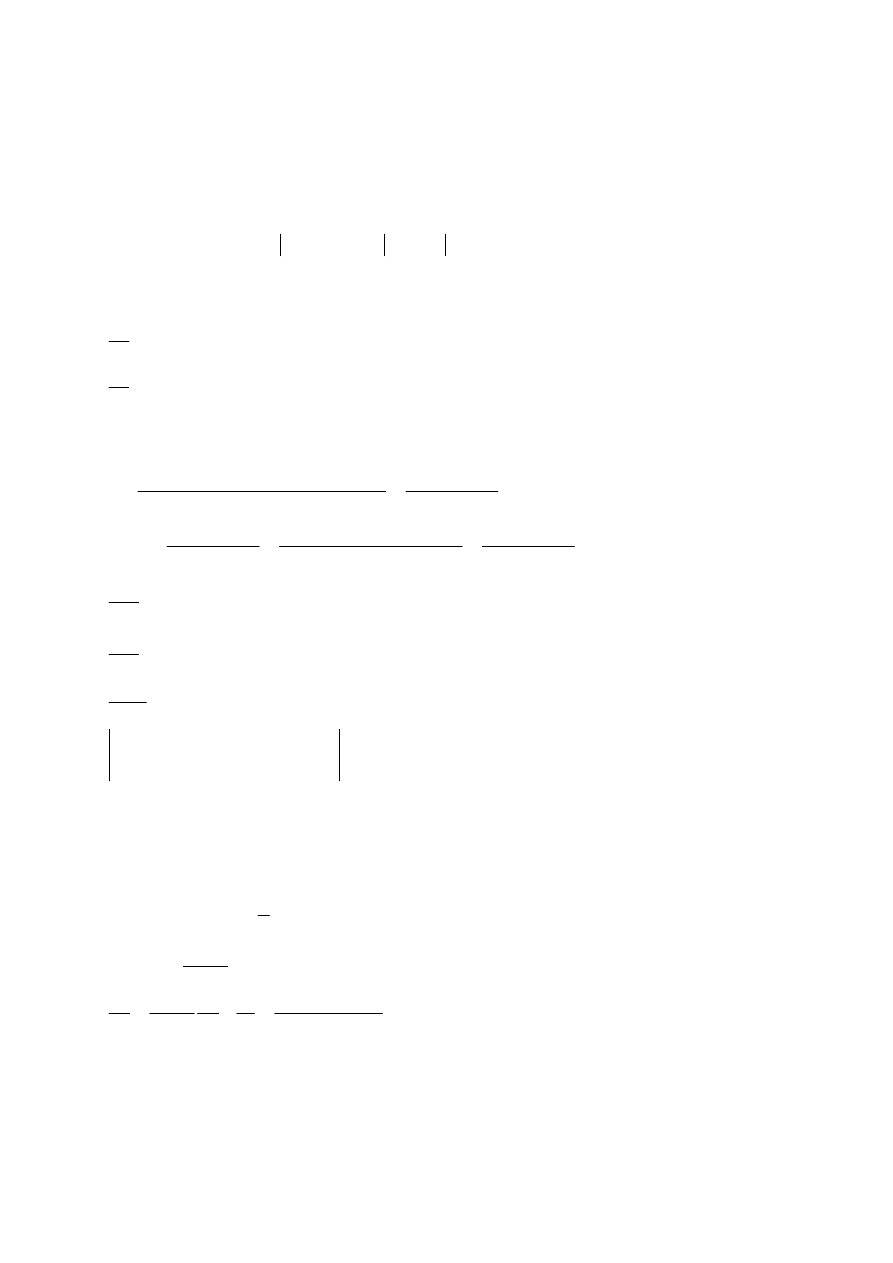
Zadanie 4
2
2
2
2
2
2
2
)
(
var
m
µ
σ
m
µ
d
ES
S
ES
+
+
=
+
=
m
µ
ES
=
2
2
)
,
cov(
)
(
m
µ
d
µ
ESEN
N
S
SN
E
+
=
+
=
(
)
(
)
( ) ( )
(
)
(
)
2
,
cov
,
cov
,
cov
)
,
cov(
d
µ
N
µ
N
N
N
E
N
S
E
N
N
S
E
N
S
=
=
+
=
(
)
=
+
−
−
+
2
2
2
2
2
2
N
bN
aSN
abS
S
a
E
(
)
(
)
min
2
2
)
(
2
2
2
2
2
2
2
2
2
2
2
2
→
+
+
−
+
−
+
+
+
+
=
m
d
bm
m
µ
d
µ
a
b
m
µ
ab
m
µ
σ
m
µ
d
a
(
)
0
2
2
2
2
2
2
2
2
2
2
2
=
−
−
+
+
+
=
∂
∂
m
µ
d
µ
m
µ
b
a
m
µ
σ
m
µ
d
a
0
2
2
2
=
−
+
=
∂
∂
m
b
m
µ
a
b
m
µ
a
m
b
−
=
(
)
(
)
0
2
2
2
2
2
2
2
2
2
2
2
2
2
=
−
−
−
+
+
+
m
µ
d
µ
m
µ
a
m
m
µ
a
m
µ
σ
m
µ
d
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
σ
m
µ
d
d
µ
m
µ
m
µ
σ
m
µ
d
m
µ
m
µ
d
µ
a
+
=
−
+
+
−
+
=
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
σ
m
µ
d
σ
m
σ
m
µ
d
m
d
µ
σ
m
µ
md
σ
m
µ
d
m
µ
d
µ
m
b
+
=
+
−
+
=
+
−
=
2
2
2
2
2
2
2
2
2
2
m
µ
σ
m
µ
d
a
+
+
=
∂
∂
2
2
2
=
∂
∂
b
m
µ
b
a
2
=
∂
∂
∂
0
4
4
4
4
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
>
−
+
+
=
+
+
m
µ
m
µ
σ
m
µ
d
m
µ
m
µ
m
µ
σ
m
µ
d
bo m>0 bo N
nieujemne
Z tego wynika, że jest to minimum
Zadanie 5
∏
=
⋅
>
=
10
1
6
1
)
10
(
i
θ
X
P
L
θ
θ
θ
L
ln
10
10
ln
6
ln
−
−
=
16
ˆ
0
)
10
(
)
10
(
10
60
10
10
10
6
2
=
→
=
−
−
−
=
−
−
=
∂
∂
θ
θ
θ
θ
θ
θ
θ
θ
θ
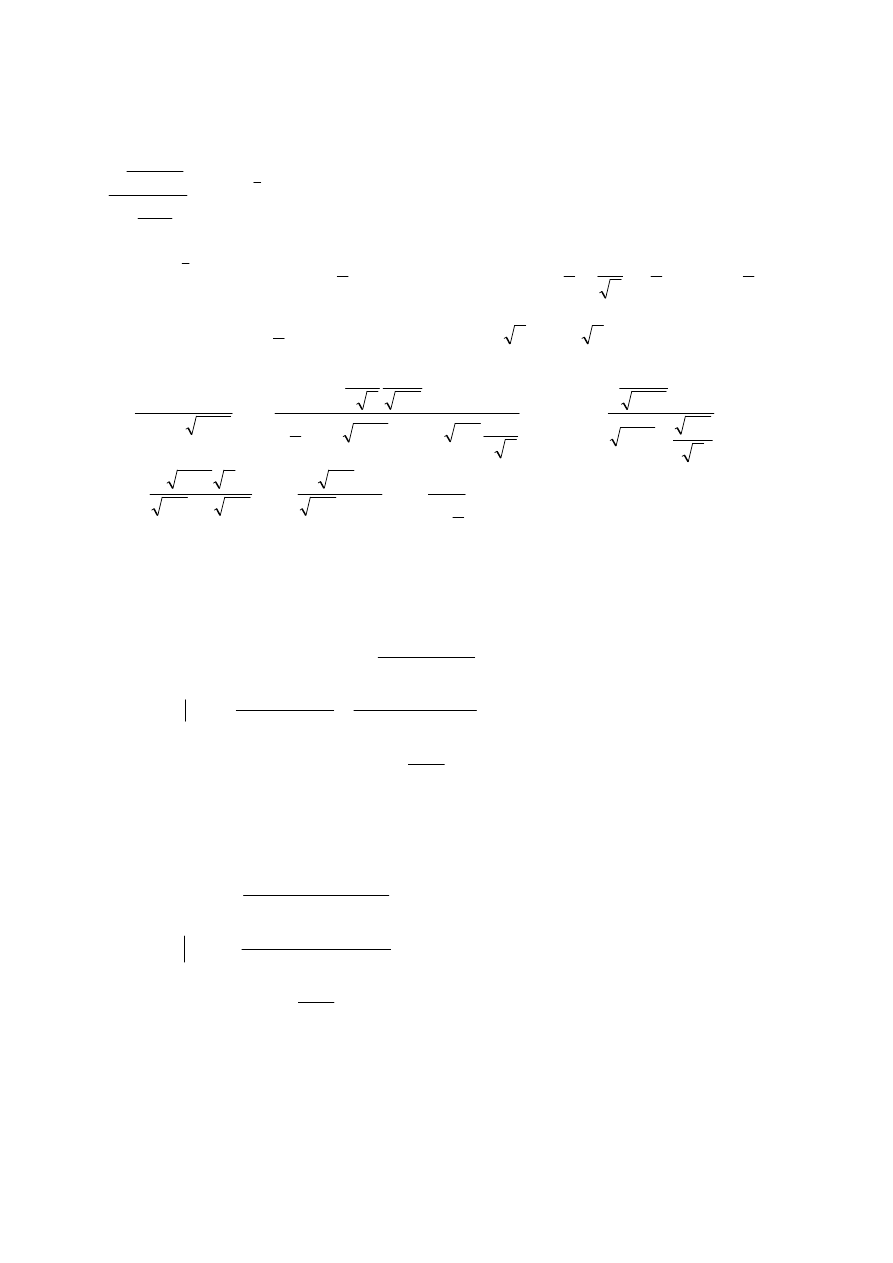
Zadanie 6
(
)
∑
∑
≅
≅
=
∑
∑
∑
−
−
−
−
)
,
(
)
,
0
(
1
0
2
2
2
1
2
2
1
n
n
N
X
n
N
X
e
e
e
H
i
H
i
n
X
X
X
i
i
i
}
n
t
n
n
t
X
P
t
n
X
P
t
e
P
N
i
n
X
i
2
1
ln
2
1
1
2
1
ln
ln
2
1
)
1
,
0
(
0
0
2
1
0
−
=
→
=
+
>
=
>
−
=
>
≅
−
∑
∑
(
)
(
) ( )
n
F
n
X
P
X
P
n
t
X
P
β
i
i
n
−
=
−
<
=
<
=
+
<
=
∑
∑
1
1
1
0
2
1
ln
=
Π
+
Π
Π
Π
=
Π
⋅
Π
−
Π
−
Π
−
=
Π
−
−
−
−
n
n
n
n
n
n
e
n
e
e
n
n
e
β
n
n
n
H
n
n
2
2
2
2
1
lim
2
2
1
2
2
2
1
2
1
2
1
lim
2
/
lim
2
/
2
/
2
/
2
/
1
1
1
1
lim
)
1
(
2
2
lim
2
2
2
lim
=
+
=
+
Π
Π
=
Π
+
Π
Π
=
n
n
n
n
n
n
Zadanie 7
(
)
(
)
( )
−
+
−
=
∩
=
=
≥
≥
≥
≥
≥
5
52
5
48
1
5
52
4
48
4
5
48
1
1
1
2
1
2
A
P
A
A
P
A
A
P
A
(
)
}
+
+
=
=
≥
5
52
4
51
5
52
48
2
48
3
3
48
3
asy
4
asy
3
asy
2
2
8
7
6
8
7
6
pik
A
A
P
B
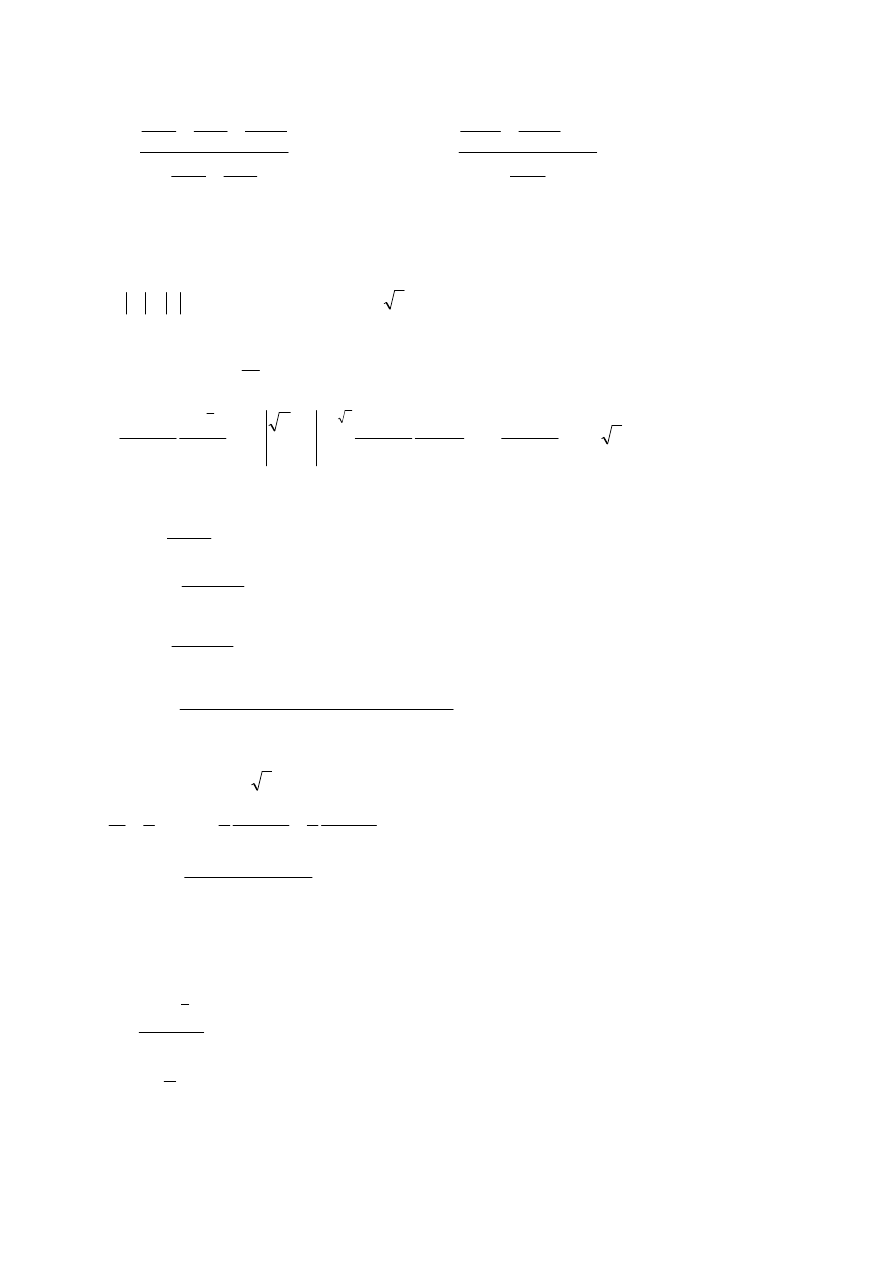
1222
,
0
!
43
!
5
!
48
!
47
!
5
!
52
!
44
!
4
!
48
4
!
43
!
5
!
48
!
47
!
5
!
52
≈
−
⋅
−
−
=
A
2214
,
0
!
47
!
4
!
51
48
!
46
2
!
48
3
!
45
!
3
!
48
3
≈
+
⋅
⋅
+
⋅
=
B
Zadanie 8
(
)
}
)
1
,
0
(
3
2
)
1
(
2
2
N
Z
Z
Y
Y
X
P
Y
X
P
χ
≅
=
<
=
<
≅
)
1
,
1
(
)
3
(
3
)
3
(
F
X
X
P
Y
X
P
Y
X
P
≅
<
=
<
=
<
=
( )
∫
∫
Π
=
Γ
Γ
=
+
Γ
=
=
=
=
+
Γ
−
3
0
2
2
2
2
2
2
1
3
0
2
)
5
,
0
(
3
)
5
,
0
(
2
1
2
)
5
,
0
(
1
)
1
(
)
5
,
0
(
1
arctg
dt
t
t
x
t
x
dx
x
x
arctgx
x
f
=
)
(
2
1
1
)
(
x
x
f
+
=
′
(
)
2
2
1
2
)
(
x
x
x
f
+
−
=
′′
(
)
3
2
2
1
2
6
)
(
x
x
x
f
+
−
=
′′′
(
) (
) ( )
( )
6
2
2
2
2
3
2
1
2
1
3
2
6
1
12
)
(
x
x
x
x
x
x
x
f
IV
+
+
⋅
⋅
−
−
+
=
rozwinięcie Taylora wokół
1
0
=
x
05
,
1
3
0
)
1
(
≈
→
≈
arctg
f
IV
bo:
6
)
1
(
8
4
2
)
1
(
2
1
)
1
(
2
1
4
3
2
−
+
−
−
−
+
Π
x
x
x
( )(
)
∑
=
−
≈
N
k
k
k
k
x
x
x
f
x
f
0
0
0
)
(
!
)
(
Z tego odpowiedź około 0,6667
Zadanie 9
n
θ
i
θ
X
L
∏
−
=
1
1
∑
−
−
=
θ
n
X
θ
L
i
ln
ln
1
1
ln
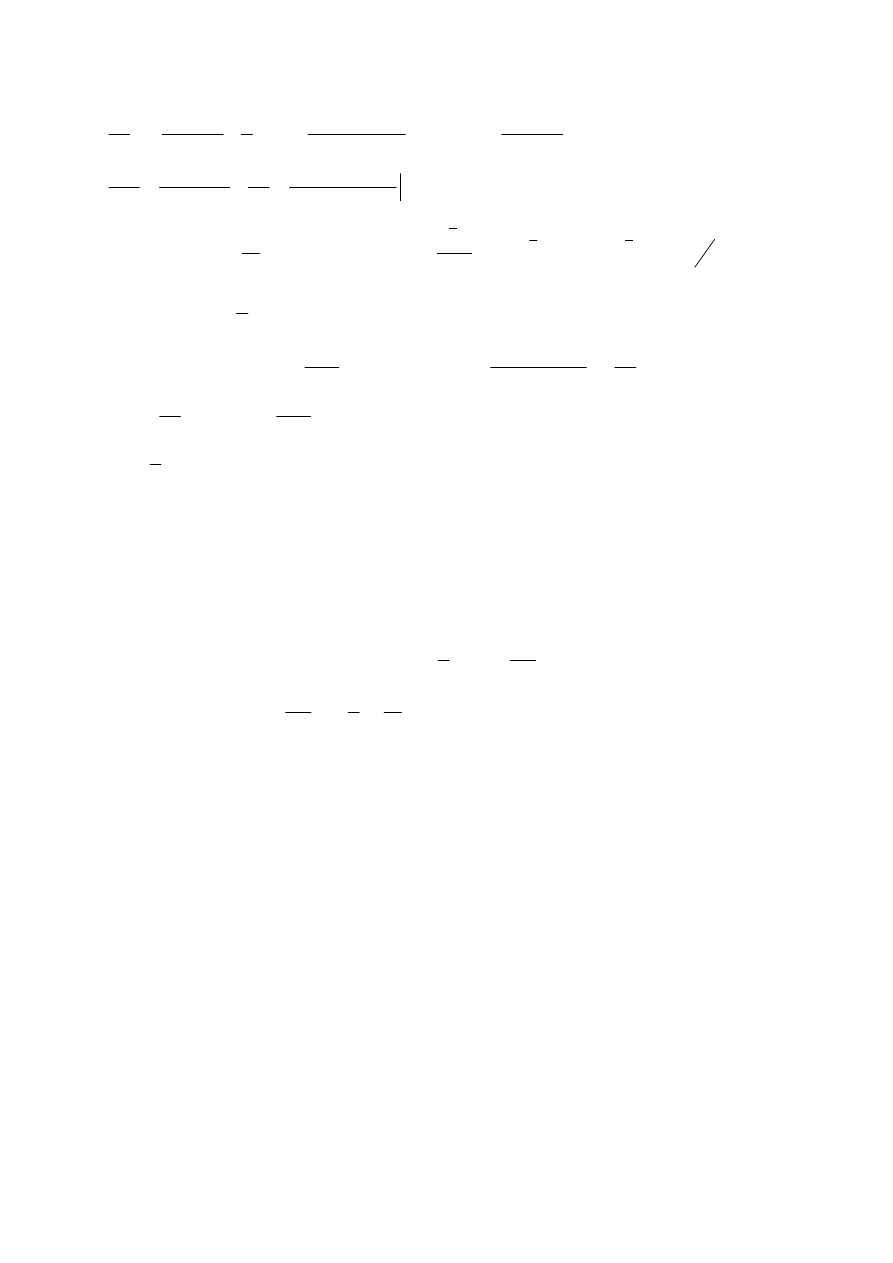
n
X
θ
θ
X
θ
n
θ
n
θ
X
θ
i
i
i
∑
∑
∑
−
=
→
=
+
→
=
−
−
=
∂
∂
ln
ˆ
0
ln
0
ln
2
2
max
0
ln
2
ln
2
ˆ
3
2
3
2
2
→
<
+
=
+
=
∂
∂
∑
∑
θ
i
i
θ
θ
n
X
θ
n
θ
X
θ
(
)
(
)
( )
∫
−
−
≅
−
=
=
=
>
=
<
=
<
−
−
−
−
1
1
1
1
1
1
1
1
ln
t
t
e
θ
t
e
θ
θ
t
t
θ
wykl
e
x
dx
θ
x
e
X
P
e
X
P
t
X
P
∑
Γ
≅
−
θ
n
X
i
1
,
ln
n
θ
n
n
n
n
θ
θ
θ
θ
n
n
θ
θ
E
θ
θ
E
θ
R
2
2
2
2
2
2
2
2
1
2
1
ˆ
2
ˆ
)
(
=
+
−
+
=
+
−
+
=
+
−
=
2
2
2
2
1
)
1
(
1
ˆ
θ
n
n
θ
n
n
n
θ
E
+
=
+
=
θ
θ
n
n
θ
E
=
⋅
=
1
ˆ
Zadanie 10
i
i
x
β
EY
=
2
2
var
σ
x
Y
i
i
=
∑
∑
=
→
=
1
i
i
i
i
x
c
β
x
c
β
( )
∑
=
→
=
→
=
i
i
i
i
i
i
nx
c
n
x
c
σ
x
c
β
1
1
gdy
min
min
ˆ
var
2
2
Z tego:
∑
∑
∑
=
=
=
i
i
i
i
i
i
x
Y
n
Y
nx
Y
c
β
1
1
ˆ
Wyszukiwarka
Podobne podstrony:
2003.10.11 prawdopodobie stwo i statystyka
2004 10 11 prawdopodobie stwo i statystykaid 25166
2004.10.11 prawdopodobie stwo i statystyka
2004 10 11 prawdopodobie stwo i statystykaid 25166
1998 10 03 prawdopodobie stwo i statystykaid 18585
2002 10 12 prawdopodobie stwo i statystykaid 21648
1996 10 26 prawdopodobie stwo i statystykaid 18572
2003.05.17 prawdopodobie stwo i statystyka
2003.12.06 prawdopodobie stwo i statystyka
2010.10.04 prawdopodobie stwo i statystyka
2003 12 06 prawdopodobie stwo i statystykaid 21710
2003 05 17 prawdopodobie stwo i statystykaid 21698
2001.10.13 prawdopodobie stwo i statystyka
2008.10.06 prawdopodobie stwo i statystyka
2007.10.08 prawdopodobie stwo i statystyka
2006.10.09 prawdopodobie stwo i statystyka
2009.10.05 prawdopodobie stwo i statystyka
więcej podobnych podstron