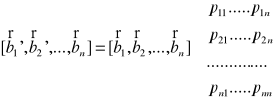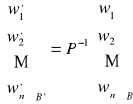WYKŁAD 6,7 |
WEKTORY I PRZESTRZENIE WEKTOROWE |
W wykładzie omówimy definicję przestrzeni wektorowej. Przedstawimy jej podstawowe własności i przykłady, w tym przestrzenie Rn. Zdefiniujemy pojęcie liniowej niezależności wektorów oraz metody jej sprawdzania.
Definicja-1 Niepusty zbiór V nazywamy rzeczywistą przestrzenią wektorową (liniową) jeśli: |
|
1 |
dla każdych
określona jest ich suma taka że |
2 |
dla każdej liczby rzeczywistej
określony jest iloczyn taki że |
Powyższe działania spełniają następujące warunki
dla dowolnych |
|
3 |
przemienność dodawania: |
4 |
łączność dodawania: |
5 |
istnienie elementu neutralnego dodawania,
tj. wektora |
6 |
istnienie elementu |
7 |
|
8 |
|
9 |
|
10 |
|
Zastępując w definicji rzeczywistej przestrzeni wektorowej liczby rzeczywiste α i β przez liczby zespolone otrzymamy definicję
zespolonej przestrzeni wektorowej.
Elementy przestrzeni V nazywamy wektorami oznaczamy je strzałkami.
Element neutralny ![]()
nazywamy wektorem zerowym przestrzeni V.
Dla operacji wprowadzonych w przestrzeni liniowej łatwo uzasadnić następujące własności:
Stwierdzenie: |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
Definicja-2 (ogólniejsza)
Przestrzeń liniowa (wektorowa) V nad ciałem K to struktura składająca się ze zbioru V którego elementy nazywamy wektorami
oraz z ciała liczbowego (K,+,•) i działań
|
Działania te mają następujące własności:
|
||
1 |
|
działanie wewnętrzne |
2 |
|
działanie łączne |
3 |
|
istnienie elementu neutralnego |
4 |
|
istnienie elementu symetrycznego |
5 |
|
działanie przemienne |
|
||
6 |
|
|
III. Działania |
||
7 |
|
rozdzielność |
8 |
|
rozdzielność |
9 |
|
łączność |
10
|
|
przeniesienie jedynki |
Wprowadzimy jeszcze pojęcie podprzestrzeni wektorowej czyli przestrzeni wektorowej zanurzonej w danej przestrzeni wektorowej.
Definicja
|
|
Niepusty podzbiór W jeśli spełnione są 2 warunki: |
|
1 |
|
2 |
|
Innymi słowami działania:
dodawania wektorów
mnożenia wektora przez liczbę
są wewnętrzne w podzbiorze W
(nie wyprowadzają poza podzbiór W)
Przykłady przestrzeni wektorowych |
Podstawowym przykładem przestrzeni liniowej jest
rzeczywista przestrzeń n-wymiarowa Rn :
![]()
Działania w ![]()
są określone następująco:
![]()
gdzie: ![]()
i ![]()
W szczególności przestrzeń R3 możemy utożsamiać ze zbiorem trójek liczb rzeczywistych [x1,x2,x3], które odpowiadają współrzędnym wektorów
w pewnym wybranym układzie współrzędnych.
Kartezjański układ współrzędnych w ![]()
Początek układu, np. punkt
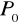
.
Trzy wzajemnie prostopadłe proste poprowadzone przez punkt
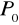
- osie x, y, z układu.Jednostki długości określone na każdej osi.
Współrzędne
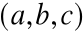
punktu P - rzuty punktu P kolejno na osie x, y, z.
y
• P(a,b,c)
x
(0, 0, 0)
z
Wektory przestrzeni wektorowej R3 zadane za pomocą trójek liczb ![]()
możemy również utożsamiać ze skierowanym odcinkiem o początku w punkcie ![]()
i końcu w punkcie ![]()
.
Podobnego utożsamienia możemy dokonać w dowolnej przestrzeni Rn.
Przykłady innych przestrzeni liniowych:
Przestrzeń Amxn macierzy o m wierszach i n kolumnach. Operacje dodawania i mnożenia w tej przestrzeni pokrywają się z poznanymi przez nas poprzednio operacjami na
macierzach:
![]()
, ![]()
![]()
,
gdzie ![]()
, ![]()
![]()
2. Przestrzeń R[x]
zbiór wszystkich wielomianów rzeczywistych
![]()
![]()
3. Przestrzeń ![]()
zbiór wielomianów rzeczywistych stopnia ≤ n
![]()
![]()
Przestrzeń funkcji T(I) określonych na przedziale

. Działania w przestrzeni T(I) wprowadzamy w sposób naturalny:
![]()
![]()
f+g
0.5
g f
0 1
![]()
Kombinacja liniowa wektorów
Definicja |
Kombinacją liniową wektorów
gdzie |
Przykład (przestrzeń ![]()
)
[4, 5, -8] = 1∙[0, 1, 0] + 2[2, 2, -4]
4[1, 2, 3] + 5[-3, 4, 2] - 4[1, 0, 1] =[-15, 28, 18]
Definicja
|
Zbiór wszystkich kombinacji liniowych ustalonych wektorów
przez symbol lin{
Wektory
lub generatorami przestrzeni lin{
|
Przykład - Przestrzeń R3
Podprzestrzeń rozpięta na wektorach ![]()
i ![]()
ma postać kombinacji wektorów o współczynnikach rzeczywistych:
![]()
i wyznacza płaszczyznę w przestrzeni przechodzącą przez punkt ![]()
w której wektory [4,3,1] i [1,2,0] są zawarte.
Przestrzeń liniowa rozpięta na zbiorze wektorów jest przykładem podprzestrzeni liniowej.
Definicja |
Skończony ciąg wektorów
dla każdego układu
albo mówiąc krócej - zachodzi implikacja:
|
Nieskończony ciąg wektorów
|
Jeżeli wektory |
Przykład
Jeżeli jeden wektor
czyli
|
Jeżeli dwa wektory
to istnieją liczby
takie, że
Jeśli np.
czyli |
Jeżeli trzy wektory
oraz
Jeżeli np.
czyli wektor (wektory te są współpłaszczyznowe)
|
Stwierdzenie |
Dwa wektory w przestrzeni R2 są liniowo niezależne wtedy i tylko wtedy gdy nie są współliniowe |
Trzy wektory w przestrzeni R3 są liniowo niezależne wtedy i tylko wtedy gdy nie są współpłaszczyznowe. |
Twierdzenie
Układ wektorów wtedy i tylko wtedy, gdy jeden spośród wektorów
|
Przykład - Przestrzeń R3
Wektory [1, 2, 3], [-3, 4, 2], [1, 0, 1] , [-15, 28, 18]
są liniowo zależne, można bowiem zauważyć że:
4[1, 2, 3] + 5[-3, 4, 2] - 4[1, 0, 1] = [-15, 28, 18]
Przykład - Przestrzeń T(I)
Funkcje ![]()
i ![]()
są liniowo niezależne w przestrzeni T[0,2π] natomiast funkcje ![]()
, ![]()
i ![]()
nie są liniowo niezależne,
gdyż ![]()
dla x![]()
[0,2π]
Z definicji liniowej niezależności wynikają następujące fakty: |
|
1 |
wektor
|
2 |
podzbiór zbioru liniowo niezależnych wektorów jest liniowo niezależny |
3 |
jeśli wektory
to zbiór wektorów
|
4 |
Zbiór
|
Liniowa niezależność wektorów w Rn
Przypomnijmy, że wektory ![]()
są liniowo niezależne wtedy i tylko wtedy, gdy macierz A o kolumnach ![]()
wymiaru n x k ma rząd k.
Zauważmy, że wówczas z tw. Kroneckera-Capelli wynika, że równanie ![]()
ma dokładnie jedno
rozwiązanie i jest to rozwiązanie zerowe ![]()
.
Ostatnie stwierdzenie jest niczym innym tylko
definicją liniowej niezależności!
Wykorzystując jeszcze raz tw. Kroneckera-Capelli możemy stwierdzić, że maksymalna liczba liniowo niezależnych wektorów w przestrzeni ![]()
wynosi n.
Twierdzenie
Żaden układ ![]()
wektorów z ![]()
nie jest liniowo niezależny.
Dowód
Macierz ![]()
ma wymiar (n)![]()
(n+1),
a zatem nie może mieć rzędu równego n+1.
Twierdzenie
Układ wektorów ![]()
o wymiarze n jest liniowo niezależny wtedy i tylko wtedy gdy:
![]()
Przykład
Sprawdzić, czy wektory są liniowo niezależne:
[1, 2, 3], [2, 3, 4], [3, 4, 5]
Wektory dane układamy jako wiersze macierzy A
i badamy czy rząd macierzy A jest równy 3.
A = 
Det A = 0 ![]()
R(A) ≠ 3 tzn. wektory są liniowo zależne.
Przykład
Wektory postaci: ![]()
i=1,2,...,n
gdzie jedynie i- ta współrzędna ≠0, są liniowo niezależne.
Oczywiście, w tym przypadku A=I a zatem ![]()
.
Wprowadzimy teraz definicję bazy przestrzeni wektorowej.
Definicja Bazą przestrzeni wektorowej V nazywamy zbiór
(1) B generuje całą przestrzeń V tj. lin{ B} = V (2) B składa się z wektorów liniowo niezależnych
|
Przykład
Sprawdzić, że układ wektorów
![]()
jest bazą w przestrzeni R2.
Warunek (1) jest spełniony, gdyż dla dowolnego ![]()
istnieje rozwiązanie równania:
![]()
mającego postać równoważną
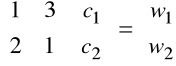
Wynika to oczywiście z faktu, że wyznacznik macierzy współczynników równania jest różny od 0.
Podobnie, aby sprawdzić warunek (2) wystarczy rozpatrzeć wektor ![]()
.Wówczas jedynym rozwiązaniem układu równań jest [c1,c2ၝ = ၛ0,0ၝ, a zatem układ ![]()
jest układem wektorów liniowo niezależnych.
Spełnione są warunki (1) (2) - rozpatrywany układ jest bazą.
Z przykładu wynika następujące ważne stwierdzenie:
Stwierdzenie
Niech
taką, że j-tą kolumną tej macierzy jest wektor Jeśli wyznacznik macierzy jest niezerowy tzn. det A≠0,
to układ
|
Udowodnimy teraz ważne twierdzenie o jednoznaczności przedstawienia wektora w bazie
Twierdzenie
Niech wektory
współczynniki są wyznaczone jednoznacznie i nazywają się
współrzędnymi wektora
|
Reprezentację ![]()
wektora w bazie B zapisujemy:
![]()
Dowód:
Z definicji bazy wynika, że wektor ![]()
jest pewną kombinacją liniowa wektorów![]()
.
Załóżmy, że wektor ![]()
posiada dwie różne reprezentacje w tej samej bazie, tzn.:
![]()
![]()
gdzie ![]()
Wówczas:
![]()
i nie wszystkie współczynniki są zerowe, co przeczy liniowej niezależności wektorów![]()
.
Zauważmy, że dla przestrzeni Rn możemy podać inny dowód tego twierdzenia.
Z twierdzenia Cramera wynika bowiem, że układ równań:
![]()
ma dokładnie jedno rozwiązanie.
Baza w przestrzeni ![]()
- układ n wektorów liniowo niezależnych.
Baza kanoniczna w przestrzeni ![]()
:
![]()
gdzie:
![]()
![]()
... ![]()
y
![]()
![]()
x ![]()
z
Każdy wektor ![]()
jest reprezentowany w bazie kanonicznej jako:
![]()
![]()
Przykład - przestrzeń R3
[-15, 28, 18] = 4[1, 2, 3] + 5 [-3, 4, 2] - 4[1, 0, 1] zatem wektor [-15, 28, 18] ma współrzędne ![]()
w bazie B={ [1, 2, 3], [-3, 4, 2], [1, 0, 1]}
Przykład
Znaleźć współrzędne wektora: ![]()
w bazie złożonej z wektorów:
![]()
![]()
![]()
w ![]()
Oznaczamy szukane współrzędne przez x, y, z;
muszą one spełniać równanie:
x[1, 1, 0] + y[1, 0, 1] + z [0, 1, 1] = [-1, -2, 3]
a zatem: x + y = -1; x + z = -2; y + z = 3
skąd: x = -3, y = 2, z = 1
Przykład : przestrzeń R3
Wektor ![]()
ma współrzędne [2, 1, -3] w bazie złożonej
z wektorów [2, 3, 0], [4, 2, 3], [1, 1, 1].
Obliczyć współrzędne wektora ![]()
w bazie
[4, 0, 1], [0, 2, 3], [2, 1, 0].
Oznaczamy szukane współrzędne przez x, y, z
2[2, 3, 0] + [4, 2, 3] -3 [1, 1, 1] =
= x [4, 0, 1] + y[0, 2, 3] + z[2, 1, 0]
Otrzymujemy układ trzech równań z 3 niewiadomymi:
4x + 2z = 5
2y + z = 5
x + 3y = 0
Postać macierzowa układu:
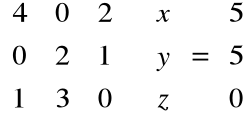
Jest to układ Cramera, gdyż wyznacznik macierzy głównej układu jest różny od zera, a zatem z twierdzenia Cramera rozwiązanie jest postaci
x = 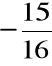
, y = ![]()
, z = ![]()
Podsumowanie
Jeżeli współrzędne wektora ![]()
∈ R3 w kolejnych bazach wynoszą odpowiednio:
[x1, x2, x3] w bazie ![]()
[y1, y2, y3] w bazie ![]()
[z1, z2, z3] w bazie ![]()
Wtedy:
![]()
![]()
![]()
Przytoczymy jeszcze twierdzenie o równoliczności baz.
Twierdzenie
Jeśli jakakolwiek baza przestrzeni liniowej V składa się z n wektorów to każda inna baza v składa się również z n wektorów |
Twierdzenie to pozwala zdefiniować wymiar przestrzeni liniowej ( ilość wektorów bazy ).
Definicja
Niech zbiór wektorów
|
Przykład
Wymiar jednoelementowej przestrzeni wektorowej zawierającej tylko wektor zerowy jest równy zero
tzn. ![]()
Przykład
Wymiar przestrzeni Rn wynosi n tzn. ![]()
Podprzestrzeń liniowa R2 składająca się z wektorów [x,y] dla których y= -x ma wymiar 1.
Wymiar przestrzeni macierzy M3x4 wynosi 12.
Uwaga
Istnieją przestrzenie liniowe nieskończenie wymiarowe. Na przykład w przestrzeni B(I) funkcje fi(x) = xi są liniowo niezależne dla i=0,1,2,... , zatem przestrzeń ta nie jest skończenie wymiarowa.
Wówczas piszemy ![]()
Dysponując współrzędnymi układu wektorów ![]()
w dowolnej bazie ![]()
możemy łatwo sprawdzić ich liniową niezależność.
Stwierdzenie
Niech
Wówczas
|
Przykład
Współrzędne wektorów ![]()
w bazie
B={ၛ1,0,0ၝ, ၛ1,1,0ၝ, ၛ1,1,1ၝ} wynoszą odpowiednio:
[2, 5, -1] [-1, 2, 3] [-5,-1, 2]
Sprawdzić, czy wektory ![]()
są liniowo niezależne.
Macierz współrzędnych wektorów ma postać:
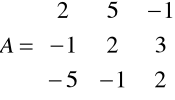
Stwierdzamy, że detA = - 62 ≠ 0 zatem R(A)=3
A więc wektory ![]()
są liniowo niezależne.
Rozpatrzmy przestrzeń liniową V wymiaru n i niech:
![]()
![]()
będą dwiema różnymi bazami przestrzeni V.
Zapiszmy wektory nowej bazy B' jako kombinacje liniowe wektorów starej bazy B o współczynnikach pij:
...................................................
|
|
Definicja
Macierzą przejścia od bazy B do bazy B' nazywamy macierz P= [pij], której kolejnymi kolumnami są współrzędne kolejnych wektorów bazy B' w bazie B.
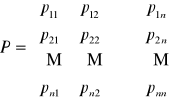
Przykład - Przestrzeń R3
![]()
jest bazą kanoniczną
B' = ![]()
={[1,0,0],[1,1,0],[1,1,1]}
Wówczas macierz przejścia od bazy B do B' ma postać
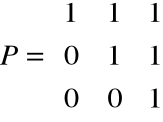
Zatem w przypadku gdy B jest bazą kanoniczną w przestrzeni Rn, macierz przejścia od bazy kanonicznej do dowolnej bazy B' składa się z wektorów tej bazy ustawionych w kolumnach.
Wyraźmy teraz wektory bazy kanonicznej przez wektory ![]()
:
![]()
![]()
![]()
Zatem odpowiednia macierz przejścia od bazy B' do bazy B
ma postać
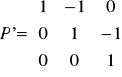
![]()
i jak łatwo sprawdzić: ![]()
.
Jest to przypadek szczególny następującego stwierdzenia.
Stwierdzenie
Jeśli P jest macierzą przejścia od bazy B do bazy B', to:
|
Stwierdzenie
Jeśli współrzędne wektora gdzie P jest macierzą przejścia od bazy B do bazy B'. |
Przykład cd.
Współrzędne wektora ![]()
w bazie B' mają postać
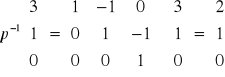
Zatem ![]()
Przestrzeń rozwiązań układu równań jednorodnych
Niech A=[aij] będzie macierzą mxn rzędu k i rozpatrzmy układ jednorodny równań liniowych
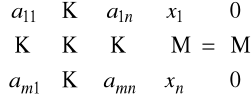
Niech S⊂ Rn będzie zbiorem wszystkich wektorów ![]()
będących rozwiązaniem układu jednorodnego.
Stwierdzenie
S jest podprzestrzenią liniową wymiaru n-k |
Podobnie, dla układu niejednorodnego
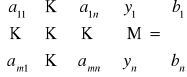
Niech T będzie zbiorem rozwiązań tego układu i niech ![]()
będzie dowolnym wektorem z T.
Stwierdzenie
Dla każdego
|
Ze stwierdzenia wynika zatem, że wszystkie rozwiązania układu niejednorodnego otrzymujemy dodając do szczególnego rozwiązania tego układu wszystkie rozwiązania układu jednorodnego.
W szczególności, dla układu trzech równań zbiór rozwiązań może być zbiorem pustym, punktem, prostą lub płaszczyzną.
Przykład
Rozpatrzmy układ równań:
2x + 3 y + 2z = 7
x + y + 2z = 4
Stosując metodę eliminacji Gaussa stwierdzamy, że zbiorem rozwiązań układu jednorodnego są wektory postaci:
[-4z, 2z, z] dla z ∈ R.
Łatwo sprawdzić, że wektor [1,1,1] jest rozwiązaniem układu niejednorodnego. Zatem ogólne rozwiązanie układu niejednorodnego ma postać:
[-4z + 1, 2z + 1, z + 1] dla z ∈ Rn.
Algebra Liniowa z Geometrią
3
![]()
Wyszukiwarka
Podobne podstrony:
Wyklad-10-a-wd, różne, Algebra semestr 1
Wyklad-01-wd-n, różne, Algebra semestr 1
Wyklad-03a-wd, różne, Algebra semestr 1
Wyklad-02-wd, różne, Algebra semestr 1
Wyklad-10-wd, różne, Algebra semestr 1
wyklad-09-wd, różne, Algebra semestr 1
wyklad-08-wd, różne, Algebra semestr 1
Wyklad-04-wd , różne, Algebra semestr 1
2008 09 KOL1, różne, Algebra semestr 1
liczby zesp.-2, różne, Algebra semestr 1
Prawo ochrony srodowiska Wyklad 06, administracja, II ROK, III Semestr, rok II, se
liczby zesp.-3, różne, Algebra semestr 1
liczby rzecz., różne, Algebra semestr 1
Z Wykład 06.04.2008, Zajęcia, II semestr 2008, Rachunek prawdopodobieństwa
fizjologia zwierzat wyklad 06 07
przyklad-kol-I, różne, Algebra semestr 1
Postepowanie administracyjne Wyklad 06, administracja, II ROK, III Semestr, rok II, sem IV, postępow
2008 09 KOL1, różne, Algebra semestr 1
więcej podobnych podstron