Na dzisiejszych zajęciach omówimy podstawowe rozkłady prawdopodobieństwa. Dzielimy je na skokowe, oraz ciągłe. Zacznijmy od skokowych. Rozkład skokowy to taki, który ma skończoną i przeliczalną liczbę wartości. Najprostszym jest rozkład jednopunktowy wyrażony tabelką:

	Punkt c
	1

Tutaj EX = c, a
. Kolejny rozkład, to rozkład dwupunktowy (zerojedynkowym). Określamy go tabelką:

	0	1
	q = 1 - p	p

Jako 0 oznaczamy sukces, a 1 - porażkę. Tutaj EX = p, oraz
. Nastepny z rozkładów to rozkład wielomianowy. Tutaj doświadczenie zerojedynkowe powtarzamy niezależnie n razy (schemat Bernulliego). Rozkład ten wykorzystywany jest w statystycznej kontroli jakości. Niech p należy do zbioru zerojedynkowego dwuelementowego i będzie ustaloną liczbą. Za X przyjmijmy zmienną losową, czyli liczbę sukcesów przyjmującą wartości od 1 do n. Funkcję porawdopodobieństwa dla tego rozkładu obliczamy z wzoru Bernulliego: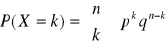
. Dla tego rozkładu EX = np (wartość oczekiwana), oraz
. Istnieje jeszcze taka ciekawostka, że:

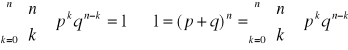
Kolejny z rozkładów, na jakim się skoncentrujemy to rozkład geometryczny, który wiąże się z powyższym rozkładem. Tym rozkładem będzie liczba doświadczeń poprzedzających pierwszy sukces. Prawdopodobieństwo, że pierwszy sukces poprzedzi k doświadczeń nieudanych będzie równe
EX dla tego rozkładu wynosi q/p, a z kolei
. I jeszcze udowodnijmy, że
.

Ostatnim z rozkładów skokowych jest rozkład Poissona. Dla
okreslamy funkcję prawdopodobieństwa:

Rozkład Poissona może dla dużych n większych równych 30 i małych p mniejszych równych 0,2 może przybliżać rozkład dwumianowy (przybliżenie Poissona):

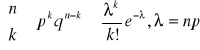
Należy też wspomnieć, że jest to jedyna sytuacja, w której
.
jest parametrem rozkładu większym od 0. I jeszcze udowodnijmy:

Popatrzmy na taki przykład. W pudełku jest 400 żarówek. Jakie jest prawdopodobieństwo, że wśród nich jest 5 żarówek wadliwych, jeśli wadliwośc produkcji żarówek wynosi 0,5 %. Jaka jest najbardziej prawdopodobna liczba uszkodzonych żarówek w tym pudełku> Zastosujemy przybliżenie Poissona:
. W tablicy rozkładu Poissona odczytamy, że P(X = 5) = 0,0361. Również w tablicy Poissona odczytamy, że najbardziej prawdopodobna liczba uszkodzonych żarówek w tym pudełku to 1 lub 2 (dla obu tych liczb prawdopodobieństwo jest równe 0,2707).

Przejdźmy teraz do rozkładów ciągłych. Jednym z nich jest rozkład jednostajny, którego gęstośc jest stała w pewnym przedziale. Gęstośc rozkładu jednostajnego w (1,b) jest określona wzorem:

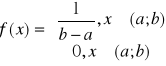
Ponieważ gęstość ta ma oś symetrii

w punkcie x = (a + b)/2, to

EX = (a + b)/2, oraz

wyliczony

przez całkowanie. Popatrzmy jeszcze niżej, jak wygląda dystrybuanta dla tego rozkładu:

No i nastepny z rozkładów to rozkład wykładniczy. Rozkład ten wystepuje często w zagadnieniach rozkładu czasu między zgłoszeniami (awariami) lub czasu oczekiwania na obsługę w systemach kolejkowych., Gęstość rozkładu wykładniczego o parametrze a > 0 ma postać:

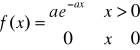
Dystrybuantą tego rozkładu jest funkcja: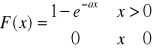
, bo
. Tutaj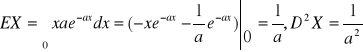
.

Zobaczmy jeszcze rysunek f(x), oraz dystrybuanty:

1. 2.

Kolejnym rozkładem jest rozkład normalny (Gaussa). Dla
określamy gęstość rozkładu:

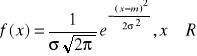
Wartości dystrybuanty dla argumentów ujemnych wyznaczamy na podstawie zależności:
. Z kolei wartości dystrybuanty
rozkładu N(0,1) można odczytać z tablicy dla x od 0 do 5 bez 5. Jeśli X ma rozkład N(m,σ), to zmienna losowa Y = (X - m)/σ ma rozkład N(0,1). Takie przekształcenie nazywamy standaryzacją, gdzie N to dowolny parametr rzeczywisty, m to wartośc oczekiwana, a σ to odchylenie standardowe. Popatrzmy jak wygląda rysunek krzywej Gaussa:

Popatrzmy jeszcze, jak wygląda dystrybuanta rozkładu N(0,1) graficznie:

Jeśli X ma rozkład N(m,σ), to wówczas stosujemy takzwane prawo trzech sigm, czyli wówczas:

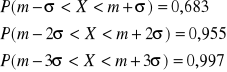
a dążące do 0

y

x

1

F(x)