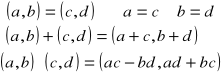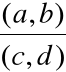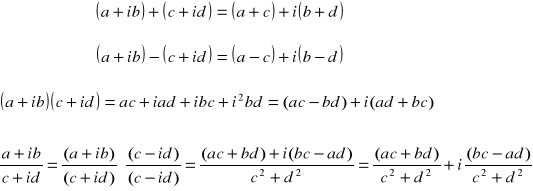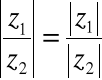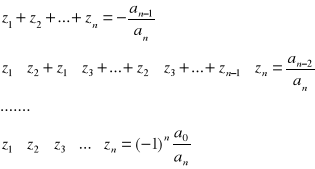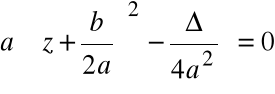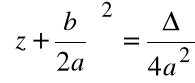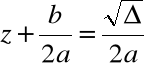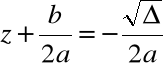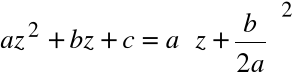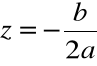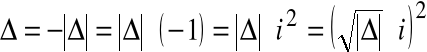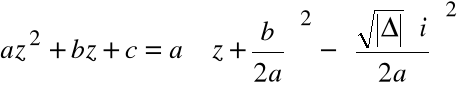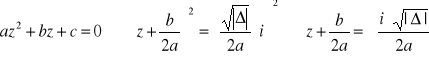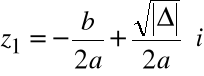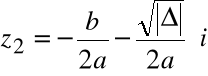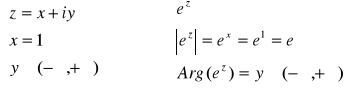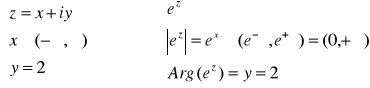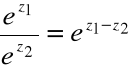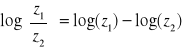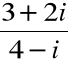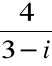WYKŁAD 2

LICZBY ZESPOLONE

Niech a, b, c, d, ... będą elementami zbioru liczb rzeczywistych R. Wprowadzimy obecnie pewne

uogólnienie liczby rzeczywistej

Będzie nim uporządkowana para liczb rzeczywistych spełniająca pewne definicje i nazwana liczbą zespoloną.

Definicja

Liczbami zespolonymi nazywamy uporządkowane pary liczb rzeczywistych, np. (a, b), (c, d)…, dla których określamy równość, dodawanie i mnożenie

w sposób następujący:

Wynikiem dodawania i mnożenia liczb zespolonych są liczby zespolone, a więc są to działania wewnętrzne.

Przykład

Obliczyć sumę i iloczyn liczb zespolonych (2,-1) i (3,7)

(2, -1) + (3, 7) = (2 + 3, -1 + 7) = (5, 6)

(2, -1)(3, 7) =
= (13, 11)

Zbiór liczb zespolonych oznaczymy literą C;

jest to początkowa litera łacińskiego słowa complexus

Zbiór liczb zespolonych jest ciałem liczbowym.

Definicja

Odejmowaniem liczb zespolonych

nazywamy działanie odwrotne do dodawania.

Wynik odejmowania liczb zespolonych nazywamy

różnicą liczb zespolonych.

(x,y) = (a,b) - (c,d) (x,y) + (c,d) = (a,b)

Z definicji dodawania i równości liczb zespolonych wynika, że wtedy x + c = a i y +d = b, czyli :

(a, b) - (c, d) = (a - c, b - d)

Zatem odjęcie od siebie dwóch liczb zespolonych polega na odjęciu wartości odpowiednich współrzędnych.

Przykład

(2,-1) - (3,7) = (2 - 3, -1 - 7) = (-1,-8).

Definicja

Dzieleniem liczb zespolonych

nazywamy działanie odwrotne do mnożenia.

Wynik dzielenia liczb zespolonych nazywamy

ilorazem liczb zespolonych.

(x, y) = (x, y)∙(c, d) = (a, b)

Z definicji mnożenia i równości liczb zespolonych wynika, że wtedy: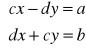

Mnożąc pierwsze równanie przez d a drugie przez c oraz odejmując pierwsze równanie od drugiego otrzymamy

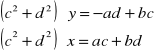
Układ ten jest zatem jednoznacznie rozwiązalny, gdy wartość
jest różna od zera, czyli gdy liczba zespolona (c, d)≠(0,0). Stąd:

Przykład

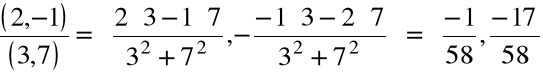
W zbiorze liczb zespolonych wyodrębniamy

zbiór elementów postaci: (a,0)

gdzie a jest dowolną liczbą rzeczywistą.

Zbiór ten utożsamiamy ze zbiorem liczb rzeczywistych.

Możemy tak zrobić dlatego, że działania na elementach (a,0) są analogiczne do działań na liczbach rzeczywistych:

(poprzedniki dodajemy i mnożymy jak liczby typu real )

W dalszym ciągu będziemy utożsamiali liczbę zespoloną (a,0) z liczbą rzeczywistą a, w szczególności liczba (0,0) będzie utożsamiana z zerem rzeczywistym.

Reprezentacje liczb zespolonych w postaci a+bi

Jedynka urojona

Liczby (0, b) różnej od zera zespolonego, nie można

w analogiczny sposób utożsamić z żadną liczbą rzeczywistą.

Definicja

Liczbę (0,1) będziemy oznaczać symbolem i :

i = (0,1)

Liczbę tę nazywamy jedynką urojoną

Urojona, dlatego że
= (-1,0) ≡ -1

gdyż ogólnie:

a w szczególności:
(0, 1)∙(0, 1)=(-1, 0)= -1

Zatem liczbę
utożsamiamy z liczbą -1

Pamiętamy że nie istnieje liczba rzeczywista,

której kwadrat byłby liczbą ujemną.

Ponieważ:

możemy liczbę zespolona (a,b) utożsamiać z wyrażeniem: a+bi zwanym

postacią kanoniczną Gaussa liczby zespolonej (a,b)

W wyrażeniu a+bi wprowadzamy nazwy:

- część rzeczywista
- część urojona

a = Re(a + bi), Re - realis - rzeczywisty (łac.)

b = Im(a + bi), Im - imaginarius - urojony (łac.)

Liczba zespolona ib, gdy
- liczba urojona.

Liczbę zespoloną będziemy dalej nazywać krótko liczbą i oznaczać także jedną litera, np. z, gdzie z = a + bi.

Działania na liczbach zespolonych w postaci kanonicznej

Definicja

Modułem liczby zespolonej z = a + bi, oznaczanym przez
, nazywamy rzeczywistą liczbę nieujemną, będącą pierwiastkiem sumy kwadratów części rzeczywistej i części urojonej tej liczby

Przykład

Stwierdzenie

Liczba zespolona jest wtedy i tylko wtedy zerem,

gdy jej moduł jest równy zeru z=0

=0

Definicja

Liczbą sprzężoną z liczbą

nazywamy liczbę postaci

Definicja

Dwie liczby, z których jedna jest sprzężona z drugą, nazywamy liczbami sprzężonymi.

Stwierdzenie

Liczby sprzężone mają równe moduły,

Iloczyn liczb sprzężonych jest równy kwadratowi ich wspólnego modułu

Wzór (ii) można napisać w postaci

Wniosek

W zbiorze liczb zespolonych sumę kwadratów można rozłożyć na iloczyn czynników pierwszego stopnia.

Przykład

Stwierdzenie

Liczba odwrotna do liczby zespolonej ma postać

dla

Iloraz liczb zespolonych ma postać

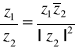
dla

Przykład

Z pierwszej równości ostatniego stwierdzenia

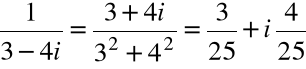
Z drugiej równości ostatniego stwierdzenia

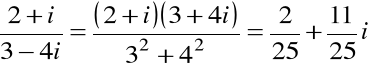
Przykład

Rozwiązanie równania kwadratowego dla

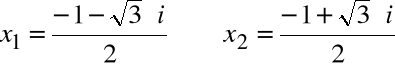
INTERPRETACJA GEOMETRYCZNA LICZB ZESPOLONYCH

Diagram Arganda

Interpretacje liczby zespolonej:

punkt P(x, y) - diagram Arganda

Liczbę zespoloną z = x + yi możemy interpretować jako:

• punkt P(x,y) na płaszczyźnie

• wektor [x,y] o początku w punkcie P(0,0)

i o końcu w punkcie P(x,y)

Płaszczyznę zespoloną oznaczymy symbolem C.

Y

X

Oś rzeczywista =Re(z)

Geometryczna interpretacja działań
dla liczb zespolonych

• Dodawanie liczb zespolonych = dodawanie wektorów

• Odejmowanie liczb zespolonych =odejmowanie wektorów

Imz

z₁-z₂ z₁ z₁+z₂

z₂

Rez

- z₂

Definicja

Argumentem liczby
, oznaczanym przez Arg (z), nazywamy każdą liczbę rzeczywistą
, spełniającą dwa warunki:

Uwaga: Argument liczby 0 nie jest określony.

Definicja

Argument główny liczby z - argument liczby z,

który należy do przedziału
.

Oznaczenie: Arg(z)

Stąd
< Arg(z)

oraz arg(z) = Arg(z) +
,
±1,...

Przykład

Arg(1) = 0, arg(1) =
, Arg(i) =
/2, arg(i) =
/2 +

Moduł liczby zespolonej -długość wektora wodzącego punktu odpowiadającego tej liczbie

Argument liczby zespolonej - miara względna kąta,

jaki tworzy wektor wodzący punktu z z osią rzeczywistą

Im(z)

z=x+yi

r=|z|

• Re(z)

0

Z rysunku wynika, że liczbę zespoloną z możemy utożsamiać z parą
, gdzie φ jest argumentem głównym z.

Takie przedstawienie nazywa się często przedstawieniem we współrzędnych biegunowych

Kąt φ jest kątem skierowanym:

Dodatnim w kierunku przeciwnym do wskazówek zegara,

Ujemnym w kierunku zgodnym ze wskazówkami zegara,

Postać trygonometryczna liczby zespolonej

r - moduł liczby zespolonej - argument liczby zespolonej

Przykład

Zapisać w postaci trygonometrycznej liczbę
posługując się jej głównym argumentem.

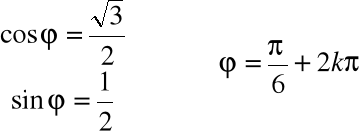
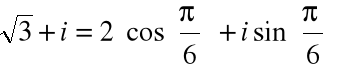
Im(z)

• z=
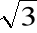
  +i

r=2

ϕ=π/6

Re(z)

Definicja

Równość dwóch liczb zespolonych w postaci trygonometrycznej

• 
  

• 
  i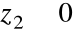
  
  

Uwaga

Zapis arg z
arg z
(mod 2
)oznacza, że argumenty liczb

z
i z
są równe modulo 2
tzn. argz
argz
+k2

Mnożenie liczb zespolonych w postaci trygonometrycznej

,

=

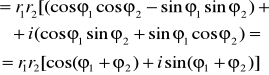
Dzielenie liczb zespolonych w postaci trygonometrycznej

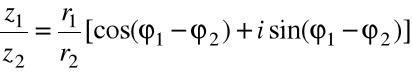
Wnioski

1	Moduł iloczynu dwóch liczb zespolonych jest równy iloczynowi ich modułów
2	Argument iloczynu dwóch liczb zespolonych jest równy sumie ich argumentów
3	Moduł ilorazu liczb zespolonych jest równy ilorazowi ich modułów
4	Argument ilorazu dwóch liczb zespolonych jest równy różnicy ich argumentów

Twierdzenie ( de Moivre'a)

Potęgowanie liczb zespolonych

Dla każdej liczby zespolonej

oraz dla liczby naturalnej
zachodzi:

Powyższe twierdzenie zachodzi również dla liczb całkowitych ujemnych:

=

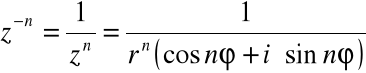
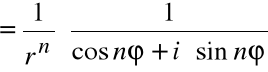
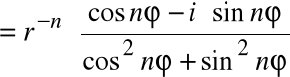
W szczególności, dla:

PIERWIASTKOWANIE LICZB ZESPOLONYCH

Funkcja: pierwiastek stopnia n

Definicja

Rozwiązania równania:

gdzie
oraz
;

nazwiemy pierwiastkami stopnia n z liczby
.

Twierdzenie

Pierwiastków stopnia n z liczby zp jest n

Wniosek

• Zapis
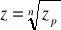
  dla liczby z nie jest jednoznaczny.

• 
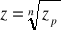
  nie jest funkcją jednoznaczną

Rozwiązanie równania:

dla trygonometrycznej postaci liczb zespolonych:

Z twierdzenia de Moivre'a:

otrzymujemy:

(1)

(2)

(3)

Układ równań (2),(3) ma rozwiązanie postaci:

czyli
gdzie

Stąd:

Łatwo zauważyć że jeśli
.

Zatem otrzymujemy n różnych wartości
,

numerowanych przez liczby
.

Pierwszy pierwiastek ( dla liczby k=0 )

nazywamy pierwiastkiem głównym

Przykład

dwa pierwiastki stopnia 2 z liczby

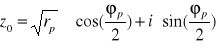
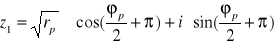
Można udowodnić że

Interpretacja geometryczna pierwiastków

Pierwiastki stopnia n są położone w wierzchołkach

n-kąta foremnego wpisanego w okrąg o środku (0, 0).

i promieniu

Zastosowanie Liczb Zespolonych.

Liczby zespolone wykorzystuje się w matematyce,fizyce, elektrotechnice (obwody prądu zmiennego).

FUNKCJE ZMIENNEJ ZESPOLONEJ

Wielomiany :

Własności wielomianów

Dwa wielomiany możemy podzielić przez siebie z resztą lub bez reszty.

Twierdzenie o podzielności wielomianów

Dla każdej pary wielomianów W(z) i P(z) gdzie stopień P(z)>0, istnieją wielomiany Q(z) i R(z) takie, że:

stopień R(z) < stopień P(z)

Powyższe przedstawienie jest jednoznaczne.

Wielomian Q(z) nosi nazwę ilorazu, a R(z) jest resztą.

Jeżeli R(z) = 0 dla każdego
to mówimy, że wielomian W jest podzielny przez wielomian P.

Przykład

Niech:

Wówczas:

Dzielenie wielomianu polega na sukcesywnym eliminowaniu najwyższych potęg wielomianu W(z).

W powyższym przykładzie
eliminuje

(po odjęciu) wyraz
wielomianu W(z)

Iloczyn
eliminuje wyraz
w reszcie.

Mamy zatem:

Ponieważ wynik odejmowania jest wielomianem stopnia 0, wzór daje wynik dzielenia W(z) przez P(z).

Ważny przypadek dzielenia wielomianów występuje gdy P(z) jest wielomianem st. 1, tzn. P(z) = z-a

Prawdziwe jest wówczas twierdzenie Bezout.

Twierdzenie Bezout

Resztą z dzielenia W(z) przez (z-a) jest W(a)

Liczba a jest pierwiastkiem wielomianu W(z) wtedy i tylko wtedy gdy

Twierdzenie

Jeśli wielomian

jest wielomianem zmiennej zespolonej, to
możemy zapisać w postaci:

gdzie
i
są wielomianami o współczynnikach rzeczywistych od zmiennych x i y.

Dowód

Z równości :
,
,
,
,...

oraz z definicji dodawania i mnożenia.

Przykład

Wniosek

Ponieważ:

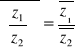
to dla wielomianu o współczynnikach rzeczywistych zachodzi:

czyli ogólnie:

Twierdzenie

Jeśli jest pierwiastkiem wielomianu o wspólczynnikach rzeczywistych to liczba sprzężona jest też pierwiastkiem wielomianu .

Krócej:

Dowód

Dla
mamy:

oraz

Stąd:

Przykład

Znaleźć wszystkie pierwiastki wielomianu

wiedząc, że jednym z nich jest
.

Rozwiązanie:

Ponieważ
jest pierwiastkiem równania również liczba do niego sprzężona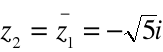

jest jego pierwiastkiem.

Z twierdzenia Bezout wynika, że wielomian w(z)

jest podzielny przez:

Iloraz z dzielenia wielomianu w(z) przez
wynosi

Wystarczy zatem rozwiązać równanie:

aby otrzymać ostatnie pierwiastki wielomianu w(z):

Uwaga

Z poprzednich twierdzeń wynika, że wielomian stopnia nieparzystego ma zawsze pierwiastek rzeczywisty.

Tak jest w istocie, ponieważ z faktu, że sprzężenie pierwiastka jest pierwiastkiem wynika, że liczba pierwiastków zespolonych jest parzysta.

Twierdzenie (zasadnicze twierdzenie algebry)

Każdy wielomian stopnia naturalnego n o współczynnikach zespolonych ma n pierwiastków w dziedzinie zespolonej

W jego postaci iloczynowej występują tylko czynniki liniowe.

Generalnie nie wszystkie pierwiastki są różne i wtedy krotność niektórych pierwiastków jest większa od 1.

gdzie
to krotności poszczególnych pierwiastków spełniające równanie:

Opierając się na postaci iloczynowej wielomianu można pokazać że spełnione są wzory Viete'a:

Uwaga:

W dziedzinie rzeczywistej ogólna postać iloczynowa może zawierać oprócz czynników liniowych również czynniki kwadratowe nierozkładalne w R czyli czynniki postaci :

W praktyce zachodzi potrzeba badania krotności pierwiastków wielomianu. Można przy tym wykorzystywać twierdzenie Bezout'a lub wykorzystać własności różniczkowania wielomianu.

Liczba z0 jest k-krotnym pierwiastkiem wielomianu W(z0) = 0, W'(z0) = 0, W''(z0) = 0, … W^(k-1)( z0) = 0 i W^(k^)(z0) ≠ 0

gdzie W^(k)(z₀) oznacza pochodną rzędu k wielomianu W dla z₀.

Twierdzenie

Każdy wielomian kwadratowy o współczynnikach rzeczywistych postaci:

W(z) =

ma w zbiorze C liczb zespolonych dwa pierwiastki

z₁, z₂ przy czym ma miejsce trychotomia:

Dowód

Postać kanoniczna wielomianu

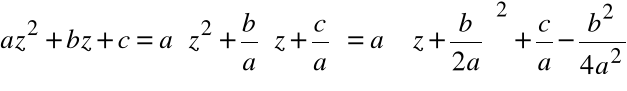
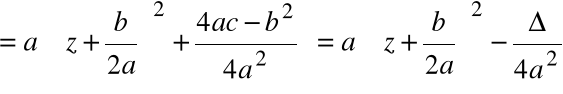
gdzie

1. , dwa różne pierwiastki rzeczywiste

2. , jeden pierwiastek o krotności 2 tj.

3. , nie ma rozwiązań w zbiorze liczb rzeczywistych W zbiorze liczb zespolonych zachodzi: Zatem: Dwa pierwiastki zespolone ,

Przykład Rozwiązać równanie:

Ponieważ

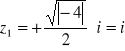
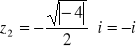
Uogólnienie powyższego twierdzenia jest następujące:

Każdy wielomian kwadratowy o współczynnikach zespolonych postaci: W(z) = ma w zbiorze C liczb zespolonych dwa pierwiastki z1, z2 : gdzie a to pierwiastek główny w sensie zespolonym. W tym przypadku w ogólności bo współczynniki są zespolone a nie rzeczywiste. Jeżeli współczynniki będą rzeczywiste (bez części urojonej) to oczywiście zachodzi:

♦Rozkład funkcji wymiernej właściwej na ułamki

proste w dziedzinie zespolonej.

Funkcja wymierna to funkcja będąca ilorazem dwóch wielomianów:

określona dla wszystkich liczb zespolonych nie będących pierwiastkami wielomianu P(z).

Jeżeli stopień W(z) >= stopień P(z) wtedy funkcję wymierną nazywamy niewłaściwą.

Jeżeli stopień W(z) < stopień P(z) wtedy funkcję wymierną nazywamy właściwą

Jeżeli stopień wielomianu W(z) jest wyższy od stopnia wielomianu P(z) to wówczas możemy wykonać dzielenie wielomianów i uzyskujemy postać:

gdzie :

• R(z) jest tożsamościowo równy zero, albo

• stopień R(z) < stopień P(z)

Wówczas funkcja R(z)/P(z) jest funkcją wymierną właściwą, którą można przedstawić jako sumę ułamków prostych.

Postać tych ułamków można wypisać po przedstawieniu P(z) w postaci iloczynowej:

Czynnikowi
odpowiada suma

ułamków prostych pierwszego rodzaju postaci:

..........

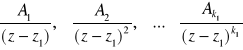
Czynnikowi

odpowiada suma ułamków prostych I rodzaju postaci

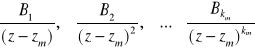
Przykład:

Rozłożyć na ułamki proste funkcję wymierną:

Funkcja podana jest już funkcją wymierną właściwą zatem nie wykonujemy dzielenia wielomianów lecz od razu wypisujemy ułamki proste zgodnie z ogólną teorią:

Dodając ułamki po prawej stronie i sprowadzając do mianownika takiego jak po lewej stronie możemy porównać liczniki:

Porównanie daje wartości stałych A, B, C, D:

A = -2, B = -i, C = 2, D = 3i

♦Rozkład funkcji wymiernej właściwej na ułamki

proste w dziedzinie rzeczywistej

Dla niektórych wielomianów uzyskamy rozkład na czynniki liniowe i wówczas postępujemy podobnie

jak dla dziedziny zespolonej.

Jednakże dla niektórych wielomianów w postaci iloczynowej mogą wystąpić czynniki kwadratowe nierozkładalne w dziedzinie rzeczywistej:

Z takimi czynnikami związane są ułamki proste II rodzaju postaci:

Zatem w rozkładzie wystąpią:

• ułamki proste I rodzaju związane z czynnikami liniowymi

• ułamki proste II rodzaju związane z czynnikami kwadratowymi nierozkładalnymi w dziedzinie rzeczywistej.

Przykład:

Rozłożyć na ułamki proste funkcję wymierną:

Zauważamy że jest to funkcja wymierna właściwa i przedstawiamy jej mianownik w postaci iloczynowej:

W postaci iloczynowej występuje:

• czynnik liniowy (x+3)

• czynnik kwadratowy
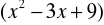
  nierozkładalny w R (delta<0)

zatem wystąpią ułamki proste I i II rodzaju:

Sprowadzając do wspólnego mianownika i porównując ułamki dostajemy:

A = -1, B = 1, C = 4

FUNKCJA LINIOWA

f : C → C

gdzie:

=

Zobaczmy jaki jest wynik iloczynu :

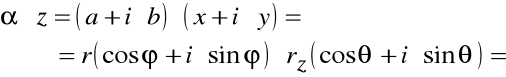
Zatem iloczyn odpowiada wydłużeniu

oraz obrotowi o kąt (
)

Zobaczmy jaki jest wynik dodawania:

Zatem dodawanie odpowiada translacji o wektor [c,d]Interpretacja geometryczna

(złożenie trzech przekształceń w płaszczyźnie )

(i) Wydłużenie(skrócenie) w stosunku

(ii) Obrót o kąt

(iii) Przesunięcie o wektor odpowiadający

Y

[c,d]

(rx,ry)

(x,y)

0 X

Przykład:

Znaleźć obraz prostokąta o wierzchołkach

w przekształceniu liniowym

Ponieważ
więc z ogólnej teorii wynika że przekształcenie to składa się z trzech przekształceń elementarnych:

• wydłużenia w skali
  

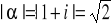
• obrotu o kąt
  

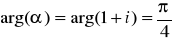
• przesunięcia o wektor
  

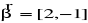
A zatem obrazem prostokąta jest prostokąt. Żeby precyzyjnie wyznaczyć jego

położenie na płaszczyźnie zespolonej można analitycznie okreslić

wierzchołki prostokąta po przekształceniu:

FUNKCJA WYKŁADNICZA: f(z) = e^z

Definicja

Dla z = x + iy, przyjmiemy (wzory Eulera)

Stąd:

Zaobserwujmy interpretację geometryczną przekształcenia f(z) = e^z.

Prześledzimy jak zmienia się w tym przekształceniu kwadrat na płaszczyźnie zespolonej:

Kwadrat ten jest częścią wspólną pasa nieskończonego ograniczonego prostymi x = 1 i x = 2 oraz pasa nieskończonego ograniczonego prostymi y = 2 i y = 3.

Zobaczmy najpierw jak przekształca się prosta x = 1.

A zatem obrazem prostej x = 1 jest okrąg o promieniu e.

Obrazem prostej x = 2 jest okrąg o promieniu e².

Wobec tego pas nieskończony zawarty między x = 1 i x = 2 przechodzi w pierścień kołowy o promieniach e i e².

Zobaczmy teraz jak przekształca się prosta y = 2.

Zatem obrazem prostej y = 2 jest półprosta o początku w punkcie (0,0) bez tego początku i nachyleniu 2 rad(1 rad≈57º).

Obrazem prostej y = 3 jest półprosta o początku w punkcie (0,0)

bez tego początku i nachyleniu 3 rad (1 rad≈57º).

Wobec tego pas nieskończony zawarty między y = 2 i y = 3 przechodzi w obszar zawarty między ramionami kąta o nachyleniu

2 rad i 3 rad.

Podsumowując kwadrat D= [1,2]x[2,3] przechodzi w przekształceniu

f(z)=e^z w wycinek pierścienia kołowego D' o promieniach e i e² zawarty miedzy promieniami o nachyleniu 2 rad i 3 rad.

Własności funkcji f(z) = e^z

Funkcja e^z jest funkcją okresową tzn.: dla

Funkcja wykładnicza a pierwiastki stopnia n

Pamiętamy że pierwiastkowanie w dziedzinie zespolonej

nie jest jednoznaczne - istnieje n pierwiastków stopnia n:

numerowanych przez liczby
.

Wzór na k-ty pierwiastek:

Jeżeli k-ty pierwiastek przedstawimy w postaci wykładniczej korzystając ze wzoru Eulera i z własności funkcji wykładniczej to:

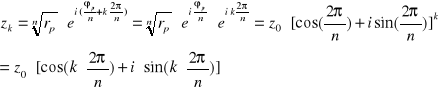
A więc k-ty pierwiastek możemy wygenerować z pierwiastka głównego poprzez pomnożenie go przez k-tą potęgę liczby:

Punktem startowym do generacji kolejnych pierwiastków

nie musi być pierwiastek główny, bowiem zachodzi również:

Wzór ten jest szczególnie użyteczny gdy chcemy przedstawić pierwiastki stopnia n w postaci kanonicznej.

Przykład:

Wyznaczyć

Zauważamy że jednym z pierwiastków jest liczba

Zatem następny pierwiastek da się obliczyć jako:

a następny czyli ostatni:

FUNKCJA LOGARYTMICZNA: f(z) = log(z) = ln(z)

Definicja

jeżeli

Uwaga: log(z) nie jest funkcją jednoznaczną ponieważ

dla
otrzymujemy:

• Funkcja log(z) ma nieskończenie wiele gałęzi:

każdej ustalonej wartości k odpowiada jedna gałąź logarytmu będąca funkcją w dotychczasowym naszym rozumieniu tego terminu.

Gałąź główna:

Zaobserwujmy jak funkcja log(z) przekształca wycinek pierścienia kołowego o promieniach e i e² zawartego między promieniami o nachyleniach 2 rad i 3 rad.

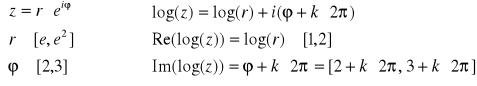
Tak więc obrazem wycinka pierścienia kołowego o promieniach e i e² zawartego między promieniami o nachyleniach 2 rad i 3 rad jest nieskończenie wiele kwadratów [1,2]x[2,3] przesuniętych

wzdłuż osi OY o wielokrotność 2π.

Własności funkcji log(z)

,

Możemy też zdefiniować w zbiorze C dowolną potęgę liczby :

Dowód:

Dla
,
mamy:

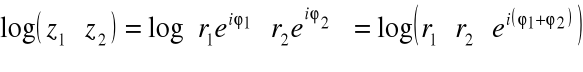
Ponadto:

.

Zadania

1. Obliczyć a) b) c) d)

2. Niech liczba ma moduł 2 i argument , a liczba moduł 1 i argument narysuj jako wektory na płaszczyźnie korzystając z postaci trygonometrycznej oblicz zapisz w postaci x+iy używając wyniku c) oblicz ponownie. Czy wynik jest zgodny z wynikiem b)

3. Korzystając z przedstawienia geometrycznego liczb zespolonych, uzasadnij kiedy

4. Rozwiąż równanie w dziedzinie zespolonej:

Poszukiwanie miejsc zerowych wielomianów

- algorytmy pierwiastnikowe

Algorytm Ferro, Tartaglii - wielomiany stopnia 3

Algorytm Ferrari - wielomiany stopnia 4

Twierdzenie Nielsa Abela i Evarista Galois Dla wielomianów stopnia ≥ 5 nie istnieje algorytm pierwiastnikowy

Algorytm poszukiwania zer wielomianu stopnia 3

Założenie:
,

jeśli nie - dzielimy obie strony równania przez
.
=

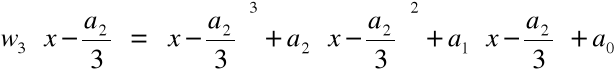
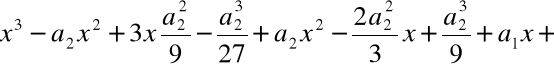
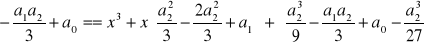
Założenie:

Krok 1. Szukamy zera wielomianu w postaci:

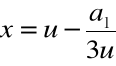
dla pewnego u

Stąd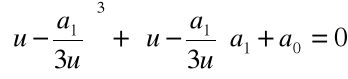

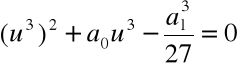
Krok 2. Przyjmujemy
i rozwiązujemy równanie

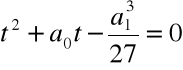
Rozwiązanie równania:

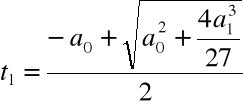
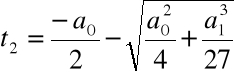
Krok 3. Wyliczamy

,

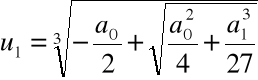
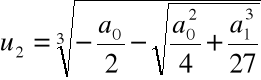
Krok 4. Wyliczamy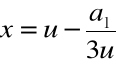
.

Przykład

Obliczyć pierwiastki wielomianu
= x³ -x+1

za pomocą algorytmu pierwiastkowego

Krok 1. Szukamy zer wielomianu w postaci:

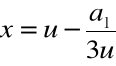
dla pewnego u

a₁= -1 zatem: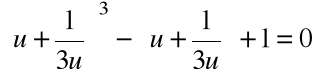

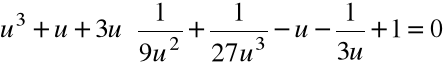
Po redukcji: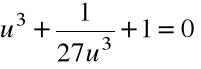

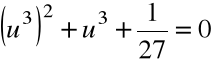
Krok 2. Przyjmujemy
i rozwiązujemy równanie:

,

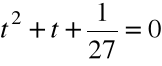
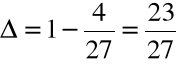
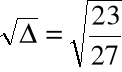
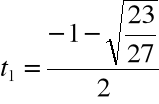
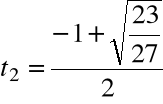
Krok 3. Wyliczamy

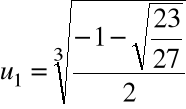
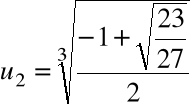
Krok 4. Wyliczamy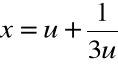
.

+

+

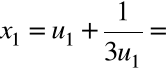
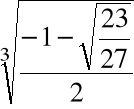
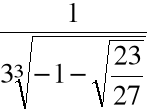
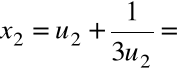
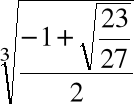
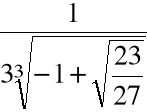
Algebra Liniowa z Geometrią

47

z=x+yi

P(x,y)

[x,y]

1

0

i

1

Oś urojona =Im(z)

---