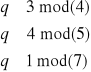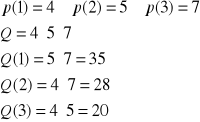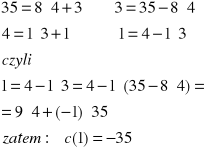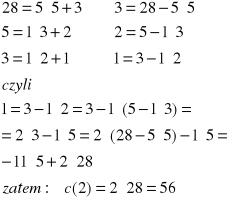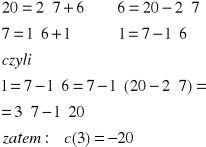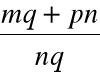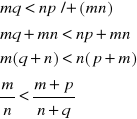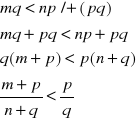WYKŁAD 1 |
WIADOMOŚCI WSTĘPNE |
Obiekty, które będą analizowane:
Skalary (liczby)
Macierze
Wektory
Punkt, prosta, płaszczyzna,przestrzeń
z=x+yi
![]()
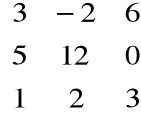
23, 15, -2, 5/7, 0
OBIEKTY SKALARNE - liczby rzeczywiste |
Zbiór liczb rzeczywistych jest sumą czterech podzbiorów:
![]()
|
Zbiór liczb naturalnych |
|
Zbiór liczb całkowitych |
|
Zbiór liczb wymiernych |
|
Zbiór liczb niewymiernych |
Jeżeli przedstawimy te podzbiory wykorzystując relację inkluzji to otrzymamy ponizszy diagram:
Reprezentacja liczb rzeczywistych na osi
Każda liczba rzeczywista jest reprezentowana jako punkt na osi liczbowej.
Każdemu punktowi na osi odpowiada jedna liczba
rzeczywista
LICZBY NATURALNE (NATURAL) |
„Liczby naturalne stworzył Bóg, wszystko inne jest dziełem człowieka” Leopold Kronecker - matematyk niemiecki (1823-1891) |
Liczby 0, 1, 2, 3,... nazywamy liczbami naturalnymi, n∈ N
Terminy pierwotne:
{ N, 0, oraz pojęcie: m jest następnikiem n (m = Nst(n)) }.
System Peano (1891):
Układ (X, xo, Nst) (X-zbiór, xo-wyróżniony element, Nst-następnik) o własnościach: |
1. xo należy do X 2. Nst przekształca X w X 3. Nst(x)≠x dla każdego x 4. [Nst(x)=Nst(y)] =>( x=y) 5. Z faktu że :
wynika że A=X
|
Aksjomat: układ (N, 0, Nst) jest systemem Peano.
Uwaga:
Przyjęcie 0 jako liczby naturalnej jest kwestią umowną.
Liczby naturalne są definiowane aksjomatycznie.
Działania na liczbach naturalnych definiowane są indukcyjnie.
Zbiór liczb naturalnych jest zbiorem podstawowym do definiowania innych zbiorów liczbowych i działań, które można w nich przeprowadzać.
Inne zbiory liczbowe są rozszerzeniem zbioru liczb naturalnych. Inne zbiory liczb tworzy się ze zbioru liczb naturalnych za pomocą różnych logicznych i algebraicznych konstrukcji.
Indukcja matematyczna - zasada kostek domina.
Zasadę indukcji matematycznej można sformułować ogólnie stosując pojęcie własności.
W(n) oznacza że liczba naturalna n ma własność W (np. spełnia określone twierdzenie).
Jeżeli : 1. istnieje liczba naturalna k taka że W(k) 2. implikacja W(n) => W(Nst(n)) jest prawdziwa
to prawdziwy jest wniosek że dla każdego n
|
Definicja indukcyjna dodawania liczb naturalnych:
(1) Jest określone dodawanie dla elementu 0:
Teza: Jest określone dodawanie liczb (m' + n): |
Wzór (1) mówi, ile wynosi dodanie 0 do dowolnego n.
Wzór (2) informuje, ile wynosi dodanie następnika m do n w zależności od sumy m + n.
Tak w sposób formalny zapisuje się znany fakt, że dodanie liczby m do n równe jest m - krotnemu dodaniu jedności.
Niech m = 0
1 + n = 0' + n = (0 + n)' = n'
(np. 1+1 = 0' + 1 = (0 + 1)' = 1' = 2)
2 + n = 1' + n = (1 + n)' = n''
(np. 2 + 1 = 1' + 1 = (1 + 1)' = 2' = 3)
...
Definicja indukcyjna mnożenia liczb naturalnych:
(1) Jest określone mnożenie dla elementu 0: (2) Zał: Jest określone mnożenie liczb (m • n)
Teza: Jest określone mnożenie liczb (m' • n): |
Tak w sposób formalny zapisuje się fakt, że mnożenie polega na powtarzaniu dodawania.
Niech m = 0
1 • n = 0' • n = (0 • n) + n = 0 + n = n
2 • n = 1' • n = (1 • n) + n = n + n
...
Potęgowanie liczb naturalnych ![]()
:
(1)
(2)
|
Rozkład liczby naturalnej na czynniki pierwsze:
Twierdzenie (Zasadnicze Twierdzenie Arytmetyki) dla każdej liczby naturalnej m > 1 istnieje dokładnie jeden zestaw liczb pierwszych p1 , p2,…, pn t.że m = p1 ∙ p2 ∙…∙ pn Ponieważ w tym iloczynie nie wszystkie liczby muszą być różne,
w rozkładzie mogą występować krotności:
|
♦ Porządek w zbiorze liczb naturalnych:
Wprowadzamy relację < nastepująco:
(m < n) <=> istnieje liczba naturalna k≠0 t.że n = m + k
Wprowadzamy również relację ≤ która oznacza :
( m ≤ n ) <=> ( m < n lub m = n )
Relacja ≤ ma nastepujące własności:
Zwrotność : n ≤ n
Antysymetria : jeżeli (m ≤ n i n ≤ m) to (m = n)
Przechodniość: jeżeli (m ≤ n i n ≤ k) to (m ≤ k)
Spójność: zachodzi (m ≤ n) lub (n ≤ m) lub (m = n)
|
Relacja posiadająca te cztery własności nazywa się relacją porządku liniowego
Mając wprowadzoną relację ≤ możemy zdefiniować pojęcie liczby najmniejszej :
n jest najmniejsza w zbiorze A <=> n ≤ a dla każdego a z A
Twierdzenie( zasada minimum ) :
W każdym niepustym podzbiorze A liczb naturalnych istnieje liczba najmniejsza
|
LICZBY CAŁKOWITE Z |
Definicja
Dla każdej liczby n![]()
N definiujemy liczbę -n.
Z = N ∪ {-1, -2, -3,...} - zbiór liczb całkowitych.
Definicja
Dodawanie liczb całkowitych:
gdy m∈ N, n = -p i m ≥ p dla pewnego p∈ N.
gdy m∈ N, n = -p i p>m dla pewnego p∈ N.
|
np.: (-5) +Z (-3) = -(5 + 3)
(2) +Z (-1) = 1 ponieważ 2 = 1 + 1
(2) +Z (-5) = -3 ponieważ 5 = 2 + 3
Definicja
Mnożenie liczb całkowitych:
m •Z n = m•n, gdy m, n ∈ N.
m •Z n = -(m • p) gdy m∈ N, n = -p, dla pewnego p ∈ N.
m •Z n = k • l gdy m = -k, n = -l dla pewnych k, l ∈ N.
|
Definicja
Odejmowanie liczb całkowitych:
m - n = u wtedy, gdy m = n + u.
|
Podzielność liczb całkowitych : krotność i reszta z dzielenia
Twierdzenie o podzielności:
Dla każdej liczby całkowitej m i liczby naturalnej n > 0 istnieje dokładnie jedna para liczb całkowitych k, r takich że:
m = k·n + r ; 0 ≤ r < n
|
Liczba k jest krotnością liczby n a r jest resztą z dzielenia .
Gdy r = 0 to mówimy że:
n dzieli m (n|m)
m jest podzielna przez n.
Przykłady:
m = 5 n = 3 to k = 1 r = 2 0 ≤ r <3
m = -5 n = 3 to k = -2 r = 1 0 ≤ r <3
W zbiorze liczb całkowitych wprowadzamy pojęcie największego wspólnego dzielnika liczb m i n : NWD(m,n).
p = NWD(m,n) <=>
|
Określony jest on z dokładnością do znaku - można przyjąć że NWD jest liczbą naturalną i rozpatrywać NWD dla liczb naturalnych m i n .
Definicja
Mówimy że liczby m,n są względnie pierwsze jeżeli NWD(m,n)=1.
Do obliczania NWD - algorytm Euklidesa.
Opiera się on na następującym fakcie:
Twierdzenie:
Jeżeli (m = k∙n + r) to (q|m i q|n q|n i q|r)
|
Wynika z niego że szukając podzielnika pary (m,n) możemy przejść do pary (n,r) itd...
Cała procedura opisana jest ciągiem równań i nierówności:
Krok-1: m = k(1)●n + r(1); ; 0 ≤ r(1) < n
Krok-2: n = k(2)●r(1) + r(2); ; 0 ≤ r(2) < r(1)
Krok-3: r(1) = k(3)●r(2) + r(3); 0 ≤ r(3) < r(2)
....
Krok-j: r(j-2)=k(j)●r(j-1)+r(j) 0 ≤ r(j) < r(j-1)
W każdym kroku NWD(r(j-2), r(j-1)) = NWD(r(j-1), r(j)).
Ciąg reszt r(j) jest ciągiem malejących liczb naturalnych więc w końcu osiągnięta zostanie wartość zero dla pewnego j=i [r(i)=0].
Wówczas : NWD(m,n) = ostatnia niezerowa reszta czyli r(i-1)
|
r(i-2) = k(i)●r(i-1) + 0; (wspólny dzielnik jest największy)
r(i-1) = NWD(r(i-2),r(i-1)) = NWD(r(i-3),r(i-2)) = NWD(r(1),r(2)) =
NWD(n,r(1)) = NWD(m,n)
Jeżeli zaczniemy wyliczać kolejne reszty z równań od ostatniego do pierwszego to dostaniemy,że
r(i-1) = NWD(m,n) = a1●m+a2●n dla liczb całkowitych a1,a2
Przykład :
Chcemy znależć NWD(19,11)-nasze kroki są następujące:
19 = 1•11 +8
11 = 1•8 + 3
8 = 2•3 + 2
3 = 1•2 + 1
2 = 2•1 + 0
Ostatnia niezerowa reszta = 1 zatem NWD(19,11) = 1.
Chcemy teraz przedstawić NWD(19,11) jako kombinację liczb 19 i 11 o współczynnikach całkowitych.Wyliczamy kolejno reszty z równań zaczynając od równania przedostatniego i idąc do góry .
1 = 3-1•2
2 = 8-2•3
3 = 11-1•8
8 = 19-1•11
Zatem NWD(19,11) = 1 = (-4)•19 + 7•11
Rozkład NWD(m,n) = a1●m + a2●n można zilustrować w
dowodzie poniższego twierdzenia:
Twierdzenie :
{ NWD(m,n) = 1 i m|(n• p) } => m|p
|
Wniosek:
Jeżeli p jest liczbą pierwszą to zachodzi następujące : p|(m•n) => (p|m) lub (p|n )
|
♦ Kongruencje
Wprowadzamy teraz relację przystawania modulo ≡ :
(p≡q) mod m r(p/m) = r(q/m) (p-q) ≡ 0 mod m |
Tutaj symbol r(p/m) oznacza ”reszta z dzielenia p przez m”
Można pokazać że jest to relacja równoważności ≈
(jest zwrotna, symetryczna, przechodnia) .
Relacja ta wprowadza podział zbioru liczb całkowitych na sumę niepustych i rozłącznych podzbiorów - klas równoważności.
Klasy równoważności tej relacji nazywamy klasami kongruencji.
Klas tych jest tyle ile jest reszt z dzielenia przez m. Zbiór reszt z dzielenia przez m zapisujemy zwykle jako ![]()
Dla liczb całkowitych wprowadzamy działania dodawania i mnożenia modulo m .
(p+q)mod m = reszta z dzielenia (p+q) przez m { r[(p+q)/m ] } (p•q)mod m = reszta z dzielenia (p•q) przez m { r[(p•q)/m] }
|
Okazuje się że działania modulo na liczbach całkowitych można sprowadzić do działań na zbiorze reszt (arytmetyka na resztach)
Przykład operacji + oraz • w zbiorze ![]()
+ |
0 |
1 |
2 |
3 |
|
• |
0 |
1 |
2 |
3 |
0 |
0 |
1 |
2 |
3 |
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
2 |
3 |
0 |
|
1 |
0 |
1 |
2 |
3 |
2 |
2 |
3 |
0 |
1 |
|
2 |
0 |
2 |
0 |
2 |
3 |
3 |
0 |
1 |
2 |
|
3 |
0 |
3 |
2 |
1 |
Twierdzenie chińskie o resztach (teoria liczb, kryptografia):
Dla każdego ciągu liczb parami względnie pierwszych p(1),p(2),...p(n) i dla każdego ciągu liczb całkowitych q(1),q(2)...q(n) istnieje liczba całkowita q taka że (q≡q(i)) mod p(i) dla i=1,2...n
|
Przykład : dla n = 2
Mamy: p(1),p(2) , NWD(p(1),p(2)) = 1, q(1) , q(2) .
Wówczas 1 = a1•p(1)+a2•p(2).
Łatwo sprawdzić że liczba q = q(2)[a1•p(1)]+q(1)[a2•p(2)]
spełnia warunki: q≡q(1)mod p(1) q≡q(2)mod p(2)
Dowód dla dowolnej liczby n wygląda następująco:
Niech Q = p(1)·p(2)...p(n) oraz Q(k) = Q/p(k)
Wtedy na podstawie założenia liczby p(k) oraz Q(k) są względnie pierwsze (NWD(Q(k),p(k)) = 1)
Jeżeli wprowadzimy oznaczenie c(k) = b(k)Q(k) to wówczas:
c(k) ≡ 1(mod p(k)) oraz c(k) ≡ 0 (mod p(m)) dla m≠k
Wtedy q= inne różnią się o wielokrotność Q.
|
Dowód ten jest dowodem konstruktywnym - podaje sposób zbudowania liczby q o podanych właśnościach.
Rozważmy przykład rozwiązania następującego układu równań kongruencji:
|
Rozwiążemy ten układ dwoma sposobami.
I sposób - metoda generowania kolejnych wielokrotności (algorytm niezbyt wydajny ale wygodny do liczenia na kartce)
|
Rozwiązujemy pierwsze równanie:
Otrzymujemy
Dobieramy teraz metodą prób krotność tak aby liczba q spełniała drugie równanie kongruencji.
Dla
Zatem po rozwiązaniu dwóch pierwszych równań
Dobieramy teraz metodą prób krotność tak aby liczba q spełniała trzecie równanie kongruencji.
Dla
Zatem po rozwiązaniu wszystkich trzech równań
|
II sposób - metoda wykorzystania konstruktywnego dowodu twierdzenia chińskiego o resztach |
Zgodnie z tym dowodem:
Znajdujemy teraz NWD(35,4)
Znajdujemy teraz NWD(28,5)
Znajdujemy teraz NWD(20,7)
|
Ostatecznie otrzymujemy :
Pozostałe liczby dają się zapisać jako |
LICZBY WYMIERNE (QUANTITY)
|
Definicja
Q - zbiór liczb wymiernych, rozszerzenie zbioru Z
Q = { ![]()
: m∈Z i n∈Z i n ≠ 0 }
Uwaga
Liczba wymierna zapisana w postaci ułamka dziesiętnego jest skończona albo okresowa.
Definicja
Działania dodawania +Q i mnożenia •Q w Q:
|
Ułamek ![]()
nazywamy nieprzywiedlnym (nieskracalnym) wtedy, gdy NWD(m,n) = 1
Definicja (dzielenie)
Dla ułamków ![]()
|
Definicja (porównywanie ułamków)
Definiujemy relację porządkującą zbiór Q:
![]()
![]()
(mq)(nq) < (np)(nq)
W tym uporzadkowaniu zbiór Q jest gęsty tzn. między
każde dwie różne liczby wymierne q1 i q2 (q1 < q2)
można wstawić trzecią liczbę q3 taką że q1< q3 <q2.
Dowód: przyjmijmy q1 = m/n q2 = p/q takie że n > 0, q > 0 i zgodnie z założeniem:
Do ostatniej nierówności dodajemy stronami iloczyn mn
Podobnie do nierówności
Zatem ostatecznie
Przyjmując teraz |
LICZBY NIEWYMIERNE (IRRATIONAL) |
Liczby niewymierne - mają reprezentację na osi liczbowej, a nie można ich zapisać jako liczby wymiernej
Np. liczba ![]()
nie jest liczbą wymierną.
![]()
0 1
Wówczas zbiór liczb wymiernych można rozłożyć na dwa podzbiory:
A= { m/n: m/n < ![]()
} B={ k/l: k/l > ![]()
}
A={1, 1.4, 1.41, 1.414, 1.4142, 1.41421, 1.414213, ...}
B={2, 1.5, 1.42, 1.415, 1.4143, 1.41422, 1.414214, ...}
Zbiór A nie ma elementu największego
Zbiór B nie ma elementu najmniejszego
Mówimy wówczas że para (A,B) wyznaczona przez liczbę ![]()
tworzy lukę w zbiorze Q .
Wniosek:
Nie każdą liczbę rzeczywistą da się zapisać w postaci ułamka zwykłego.
Liczby, które takiego zapisu nie mają nazywamy niewymiernymi i oznaczamy \Q .
LICZBY RZECZYWISTE (REAL) |
Zatem zbiór liczb rzeczywistych jest sumą zbioru liczb wymiernych Q i zbioru liczb wyznaczających luki.
R = Q ∪ \Q
♦ Systemy pozycyjne w R
Każdą liczbę rzeczywistą s da się przedstawić jako sumę liczby całkowitej i liczby ułamkowej:
![]()
Część całkowitą z dokładnością do znaku da się przedstawić w systemie pozycyjnym o podstawie m>1:
![]()
Współczynniki ![]()
są resztami z dzielenia przez liczbę m
![]()
Część ułamkową da się przedstawić w systemie pozycyjnym o podstawie m>1:
![]()
Współczynniki ![]()
są resztami z dzielenia przez liczbę m
![]()
Ze wzoru na przedstawienie liczby całkowitej wynika algorytm znajdywania cyfr liczb reprezentacji ![]()
w danym systemie pozycyjnym o podstawie m.
Liczby te znajdujemy przez kolejne: dzielenie przez podstawę m określanie reszty z tego dzielenia, określanie krotności.
Przykład: liczbę (23)10 przedstawić w postaci dwójkowej.
Podstawa 2
krotność |
reszta |
ai |
23 |
1 |
ao |
11 |
1 |
a1 |
5 |
1 |
a2 |
2 |
0 |
a3 |
1 |
1 |
a4 |
0 |
0 |
stop |
A zatem wynik naszego algorytmu zapisujemy następująco:
(23)10 = (10111)2
Ze wzoru na przedstawienie liczby ułamkowej wynika algorytm znajdywania liczb reprezentacji ![]()
w danym systemie pozycyjnym o podstawie m.
Liczby te znajdujemy przez kolejne: mnożenie przez podstawę m, zapamiętywanie częsci całkowitej i wydzielanie części ułamkowej.
Przykład: liczbę (0.75)10 przedstawić w postaci dwójkowej.
Podstawa 2
Część ułamkowa |
Wynik mnożenia |
Część całkowita |
bi |
0.75 |
1.5 |
1 |
b1 |
0.5 |
1.0 |
1 |
b2 |
0 |
0 |
0 |
stop |
A zatem wynik naszego algorytmu zapisujemy następująco:
(0.75)10 = (0.11)2
♦ Przedstawienia dziesiętne liczb rzeczywistych
Liczba wymierna może mieć przedstawienie dziesiętne:
|
Liczba niewymierna ma przedstawienie dziesiętne:
|
♦ Zbiór liczb rzeczywistych z opisanymi działaniami dodawania i mnożenia jest ciałem liczbowym
|
Liczba zespolona - para liczb.
Definicja
Liczbami zespolonymi nazywamy uporządkowane pary liczb rzeczywistych, np. (a, b) , (c, d) ,
dla których określamy:
równość,
dodawanie
mnożenie
w sposób następujący:
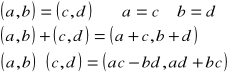
Dodawanie i mnożenie liczb zespolonych są
działaniami wewnętrznymi w zbiorze liczb zespolonych
tzn. ich wynik pozostaje w tym zbiorze(jest liczbą zespoloną)
WEKTORY |
Przestrzeń = zbiór punktów
Przestrzeń jednowymiarowa 1D - oś liczbowa
Przestrzeń dwuwymiarowa 2D - płaszczyzna
Kartezjański układ współrzędnych w przestrzeni 2D
Początek układu, np. punkt
2 wzajemnie prostopadłe proste - osie x, y układu.
Jednostki długości określone na każdej osi.
Współrzędne punktu
- rzuty punktu kolejno na osie x, y.
3. Przestrzeń trójwymiarowa 3D - przestrzeń
Kartezjański układ współrzędnych w przestrzeni 3D
Początek układu, np. punkt
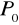
3 wzajemnie prostopadłe proste - osie x, y, z układu.
Jednostki długości określone na każdej osi.
Współrzędne punktu
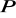
- rzuty punktu na osie x, y, z.
4. Przestrzeń czterowymiarowa - czasoprzestrzeń
P(x,y,z,t).
5. Przestrzeń naprężeń w materiale: 6 - wymiarowa.
6. Uogólnienie na przestrzeń n - wymiarową
Przestrzeń Euklidesowa n - wymiarowa, ![]()
Punkt przestrzeni ![]()
- układ n liczb ![]()
MACIERZE |
Zadanie-1:
Mamy dane miasta: Londyn, Madryt, Nowy Jork i Tokio. Wyznaczyć diagram odległości pomiędzy tymi miastami.
I etap:
Tworzymy wektor, którego współrzędnymi są odległości od Londynu do każdego z miast:
Odległość od Londynu do Londynu = 0
Odległość od Londynu do Madrytu = 785
Odległość od Londynu do Nowego Jorku = 3459
Odległość od Londynu do Tokio = 5959
Otrzymujemy wektor: L = [0, 785, 3469, 5959]
Analogicznie tworzymy wektor odległości od Madrytu do każdego z miast: M = [785, 0, 3593, 6706]
Wektor odległości od Nowego Jorku do każdego z miast:
NY = [3469, 3593, 0, 6757]
Wektor odległości od Tokio do każdego z miast:
T = [5959, 6706, 6757, 0]
II etap.
Możemy zgromadzić teraz te wektory w jednej tablicy, otrzymując zestawienie odległości pomiędzy miastami. Taką tablicę nazywamy macierzą.
Londyn Madryt N. Jork Tokio

Zadanie-2: Zagadka Einsteina
Krąży legenda, że tę zagadkę wymyślił Albert Einstein. Podobno powiedział też, że 98% ludzi nie jest w stanie jej rozwiązać.
Pięciu ludzi (Szwed,Duńczyk,Niemiec,Anglik,Norweg) mieszka w pięciu różnych domach, o różnych kolorach (żółty,zielony,czerwony,niebieski,biały) Wszyscy palą pięć różnych marek papierosów (Rothmans,Pall Mall,Dunhill,Marlboro,Philip Morris) i piją pięć różnych napojów(kawa,herbata,woda,mleko,piwo)
Poza tym jeszcze hodują zwierzęta pięciu różnych gatunków (konie,koty,psy,ptaki,rybki) |
|
Dom-1 |
Dom-2 |
Dom-3 |
Dom-4 |
Dom-5 |
Narodowość |
|
|
|
|
|
Kolor domu |
|
|
|
|
|
Co pali? |
|
|
|
|
|
Co pije? |
|
|
|
|
|
Co hoduje? |
|
|
|
|
|
|
Dom-1 |
Dom-2 |
Dom-3 |
Dom-4 |
Dom-5 |
Narodowość |
Norweg
|
Duńczyk |
Anglik |
Niemiec |
Szwed |
Kolor domu |
Żółty
|
niebieski |
czerwony |
zielony |
biały |
Co pali? |
Dunhill
|
Rothmans |
Pal Mal |
Marlboro |
Philip Morris |
Co pije? |
Woda
|
herbata |
mleko |
kawa |
piwo |
Co hoduje? |
Koty
|
konie |
ptaki |
RYBKI |
psy |
Rozwiązanie Rybki hoduje Niemiec
Algebra Liniowa z Geometrią
24
Q
R
\Q
Z
N
0
![]()
1/2
2
1
-1
Londyn
Madryt
Nowy Jork
Tokio
Wyszukiwarka