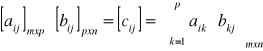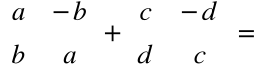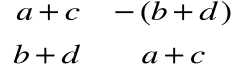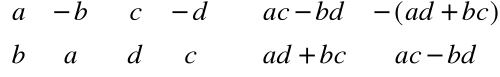WYKŁAD - 3

ALGEBRA MACIERZY

Definicja

Macierzą rzeczywistą (zespoloną) wymiaru mxn,

gdzie
, nazywamy tablicę prostokątną
liczb rzeczywistych (zespolonych) ustawionych

w m wierszach i n kolumnach

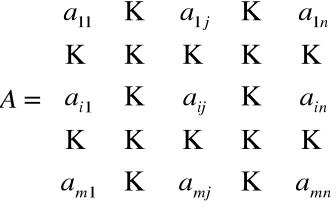
i-ty wiersz

j-ta kolumna

Element stojący na przecięciu i-tego wiersza i j-tej kolumny będzie oznaczany przez a_ij. Macierz A o elementach a_ij zapisywana jest jako
lub
.

W definicji macierzy przypisujemy parze (i,j)

(miejscu na przecięciu i-tego wiersza i j-tej kolumny)

liczbę a_ij , zatem macierz jest wartością funkcji odwzorowującej iloczyn kartezjański (1, ... , m) x (1, ... , n)

w zbiór liczb rzeczywistych lub zespolonych:

Rodzaje macierzy

Macierz kwadratowa stopnia n:

Macierz o wymiarze nxn

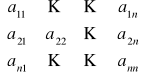
Elementy macierzy mające ten sam numer wiersza i kolumny tworzą (główną) przekątną macierzy.

Macierz diagonalna stopnia n:

Macierz kwadratowa stopnia n, w której wszystkie elementy poza główną przekątną są równe 0.

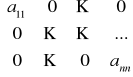
Macierz jednostkowa stopnia n:

Macierz diagonalna, której przekątna składa się z samych jedynek. Oznaczamy ją I_n lub I.

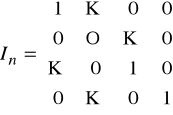
Macierz kolumnowa (wektor kolumnowy):

macierz o wymiarze mx1

Macierz wierszowa: (wektor wierszowy)

macierz o wymiarze 1xn

Macierzą trójkątną dolną nazywamy macierz w której elementy leżące nad górną przekątną są równe 0.

Analogicznie w macierzy trójkątnej górnej

elementy pod dolną przekątną są równe 0.

Macierz zerowa oznaczona 0 lub 0_mxn jest macierzą wymiaru
składającą się z samych 0.

Przykład

Macierz kolumnowa wymiaru 3,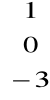

Macierz wierszowa wymiaru 4,

Macierz o wymiarze 2x3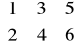

Macierz dolno-trójkątna stopnia 2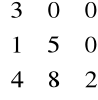

Definicja

Macierze A i B nazywamy równymi ( A = B),

jeżeli mają ten sam wymiar mxn

oraz a_ij = b_ij dla i = 1, ... , m oraz j = 1, ... ,n.

Przykład

,

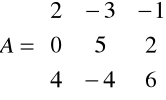
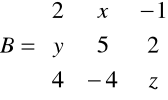
Przykład

Przedstawienie danych w postaci macierzy - zestawienie odległości pomiędzy miastami

Londyn Madryt Nowy Jork Tokio

Macierz liniowego układu równań

Ogólna postać układu m - równań liniowych algebraicznych z n - niewiadomymi

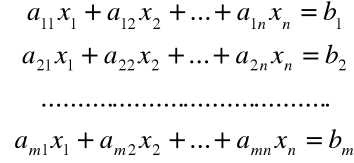
niewiadome:

Z układem m równań liniowych z n niewiadomymi możemy związać następujące trzy macierze:

1. Macierz A współczynników zwana macierzą główną układu równań

A=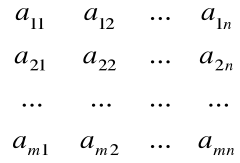

2) Wektor kolumnowy B zwany macierzą wyrazów wolnych układu równań

B =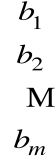

3) Wektor kolumnowy X, zwany macierzą rozwiązań układu równań

X =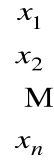

Zdefiniujemy teraz podstawowe działania na macierzach: dodawanie, odejmowanie, mnożenie przez liczbę, mnożenie dwóch macierzy.

DODAWANIE MACIERZY

Definicja

Sumą macierzy
i
wymiaru m
n, nazywamy macierz C =
wymiaru m
n taką, że

Przykład

=

=

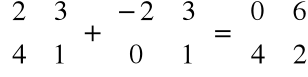
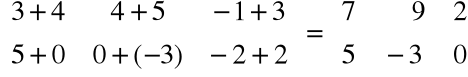
Analogicznie różnica macierzy A i B, C=A-B jest macierzą wymiaru mxn taką, że

Przykład

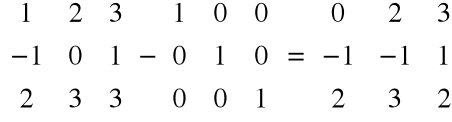
MNOŻENIE MACIERZY PRZEZ LICZBĘ

Definicja

Dla macierzy
i liczby rzeczywistej λ

.

Mnożąc macierz A przez liczbę λ ,

mnożymy każdy wyraz macierzy przez λ .

Układ równań liniowych m
n możemy zapisać w postaci

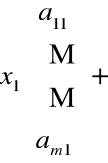
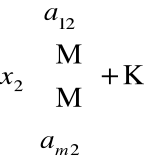
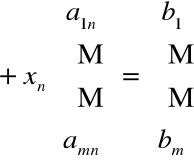
Przykład

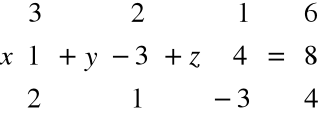
MNOŻENIE MACIERZY

Definicja

Jeżeli A =
jest macierzą wymiaru m
p

oraz B =
jest macierzą wymiaru p
n to

iloczynem macierzy A i B nazwiemy macierz C=
wymiaru m
n określoną jako

gdzie:

inaczej A • B =

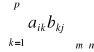
Praktyczny sposób mnożenia macierzy

• Wybieramy i - ty wiersz macierzy A tzn. (
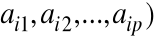
  oraz j - tą kolumnę macierzy B tzn. (b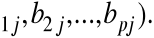
  

• Mnożymy kolejno odpowiednie wyrazy wybranego wiersza i wybranej kolumny przez siebie i otrzymane iloczyny dodajemy, otrzymując wyraz c
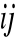
  macierzy C.

Ważne !

• mnożenie macierzy w ogólnym przypadku

nie jest przemienne

• nie zawsze można pomnożyć dwie macierze: jest to możliwe tylko wtedy gdy liczba kolumn macierzy A jest równa liczbie wierszy macierzy B.

Przykład

A =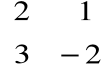
, B =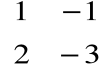

A • B =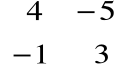
B • A =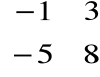

A • B
B • A

Przykład

=

=

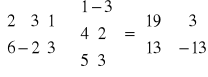
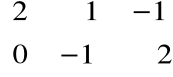
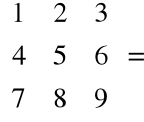
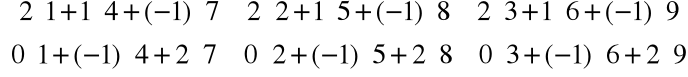
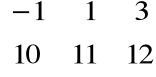
Przedstawienie macierzowe układu równań liniowych

Ogólna postać układu m - równań liniowych algebraicznych z n - niewiadomymi

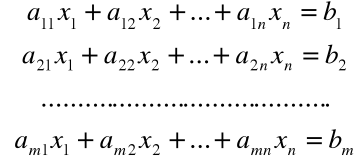
niewiadome:

Wykorzystując definicję mnożenia macierzy, możemy w sposób zwarty zapisać układ równań liniowych jako

A• X = B

gdzie

A=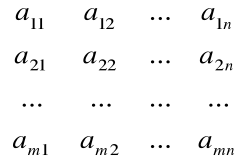
B =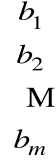

X =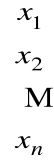

Rzeczywiście, lewa strona jest macierzą wymiaru mx1 czyli wektorem kolumnowym wymiaru m, a jej i-ty element jest równy

Jednocześnie i-ty element wektora kolumnowego B jest równy
.

Przykład

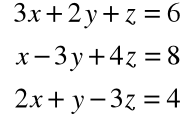
A =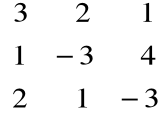
B =
X =

=

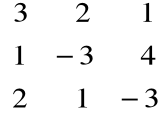
A
X = B

WŁASNOŚCI DZIAŁAŃ MACIERZOWYCH

Twierdzenie

Działania dodawania i mnożenia macierzy mają następujące własności:

1. A+ B=B+A (przemienność dodawania)

2. (A+B)+C=A+(B+C) (łączność dodawania)

3. A+ 0=0 + A gdzie 0 jest macierzą zerową

4. A• (B • C) = (A • B) • C (łączność mnożenia)

5. A • (B + C) = A • B + A • C

6. (A + B) • C = A • C + B • C

7. Jeśli A =
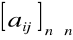
   i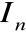
   jest macierzą jednostkową

stopnia n to A• I = A = I • A

Dowód:

Własności (1)-(7) wynikają z definicji działań na macierzach.

Twierdzenie

Niech
oznacza macierz przeciwną do macierzy A.

Dla dowolnych macierzy A i B zachodzą następujące związki:

• 
  

• 
  

• 
  

Definicja

Jeżeli A =
jest macierzą wymiaru m
n, wtedy macierz wymiaru n
m, oznaczoną przez A

gdzie
, nazywamy

macierzą transponowaną do macierzy A.

Przykład

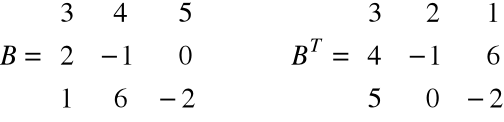
Transpozycja macierzy polega więc na zamianie miejscami kolumn i wierszy macierzy w ten sposób,

że pierwszy wiersz staje się pierwszą kolumną itd.

Twierdzenie (własności transpozycji)

Dla macierzy A i B zachodzi

• 
  

• 
  

• 
  

Macierz A jest symetryczna

Przykład

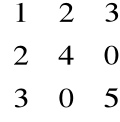
Macierz symetryczna

Przykład

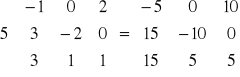
Podsumowanie działań macierzowych

Nazwa działania	Zapis działania
Suma Macierzy	[aij]mxn+[bij]mxn=[aij+bij]mxn
Różnica macierzy	[aij]mxn-[bij]mxn=[aij-bij]mxn
Mnożenie macierzy przez liczbę	λ∙[aij]mxn=[λ∙aij]mxn
Mnożenie dwóch macierzy
Transpozycja macierzy

POSTAĆ MACIERZOWA PRZEKSZTAŁCEŃ PŁASZCZYZNY

Przesunięcie

Punkty na płaszczyźnie (x, y) możemy przesunąć na nową pozycję dodając do współrzędnych punktów wielkość przesunięcia.

Dla każdego punktu P(x, y), który ma być przesunięty do nowego punktu P'(x', y') o d_x jednostek wzdłuż osi x i o d_y jednostek wzdłuż osi y, możemy napisać:

x' = x+ d_x y' = y+ d_y

Zapis w postaci macierzowej:

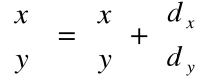
Przesunięcie prostokąta:

Skalowanie

Punkty mogą być skalowane ze współczynnikiem
wzdłuż osi x i ze współczynnikiem
wzdłuż osi y przez mnożenie:

x' =
y' =

Zapis w postaci macierzowej:

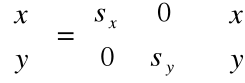
Skalowanie prostokąta ze współczynnikiem ½ w kierunku osi x i ¼ w kierunku osi y (skalowanie niejednorodne).

Obrót

Punkty mogą być obracane o kąt θ wokół początku układu współrzędnych.

Definicja obrotu:

Zapis w postaci macierzowej:

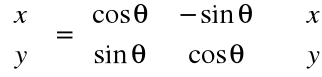
Kąty dodatnie - kierunek przeciwny względem kierunku ruchu wskazówek zegara od x do y.

Kąty ujemne - kierunek zgodny z kierunkiem ruchu wskazówek zegara.

W równaniach określających nowe współrzędne można skorzystać z tożsamości:

.

Równanie:

można wyprowadzić korzystając z rysunku, na którym obrót o kąt θ przekształca punkty

Odległości od początku układu współrzędnych punktów P' i P są równe i wynoszą r.

oraz

Przekształcenie afiniczne (powinowactwo)

Przekształcenie liniowe niejednorodne postaci

gdzie det(A) ≠ 0

• A - macierz kwadratowa wymiaru nxn

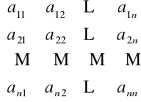
• X,Y - punkty przestrzeni n-wymiarowej

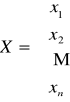
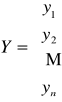
• Macierz wyrazów wolnych

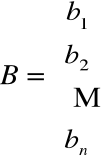
Nieosobliwość macierzy A zapewnia odwracalność przekształcenia

Przekształcenie afiniczne zachowuje pewne własności figur zwane niezmiennikami afinicznymi.

Niezmiennikami przekształceń afinicznych są:

• prosta, odcinek, wektor

• współliniowość punktów

• równoległość prostych, wypukłość figur,

• trójkąt, równoległobok,

• równość wektorów,

• stosunek długości równoległych odcinków

• stosunek pól figur (na płaszczyźnie),

• stosunek pól figur na płaszczyznach równoległych

• elipsa, parabola, hiperbola.

Przekształcenie afiniczne może być zapisane w postaci klatkowej

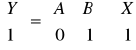
Dzięki temu składanie przekształceń afinicznych może być wykonywane tylko za pomocą mnożenia macierzy.

UWAGA:

W bibliotekach języka programowania Java dotyczących grafiki dwuwymiarowej (klasa Graphics2D) znajduje się klasa AffineTransform reprezentująca przekształcenie afiniczne.

Jak już wiemy jest to przekształcenie liniowe zachowujące m.in. prostoliniowość i równoległość prostych.

Przekształcenie afiniczne na ogół zmienia długość odcinków

i kąty.

Przekształcenie to punktowi (x,y) płaszczyzny 2D przyporządkowuje punkt (x',y') płaszczyzny i może być reprezentowane przez macierz 3x3 i przedstawione analitycznie w postaci:

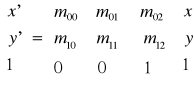
Przekształcenie afiniczne można uzyskać ze złożenia przekształceń elementarnych:

• przesunięcia( ang. translation),

• obrotu(ang. rotation),

• skalowania (ang.scaling),

• symetrii osiowej (ang.flip)

• ścinania (ang. shear)

Macierz tranlacji ma w tej notacji postać:

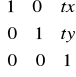
Macierz obrotu w tej notacji ma ma postać:

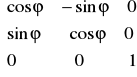
Macierz skalowania w tej notacji ma ma postać:

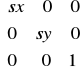
Macierz ścinania w tej notacji ma ma postać:

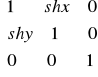
Macierze a liczby zespolone

Macierze postaci

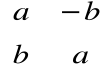
, gdzie

są reprezentacją liczb zespolonych postaci
.

Definicja równości, dodawania, mnożenia tych macierzy jest analogiczna do definicji równości, dodawania i mnożenia liczb zespolonych.

• 
  

• 
  
  

• 
  

• macierzą przeciwną do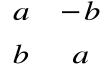
jest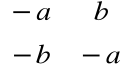

• macierzą odwrotną do niezerowej macierzy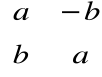

jest macierz:

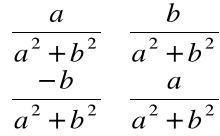
• macierzą odpowiadającą jedności rzeczywistej jest

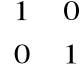
• macierzą odpowiadającą jedności urojonej jest

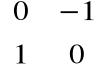
Macierze zespolone:

Macierz zaspolona to macierz której elementy są liczbami zespolonymi.

Definicja

Macierz
sprzężona do A to macierz zawierająca elementy będące liczbami zespolonymi sprzężonymi

do elementów macierzy A:

Własności sprzężenia macierzy:

1.

2.

3.

4.

5.

Transponowaną macierz sprzężoną do A

oznaczamy przez
.

Definicja :

Macierz A nazywamy macierzą hermitowską (samosprzężoną) jeżeli zachodzi warunek:

Z definicji tej wynika że:

• macierz hermitowska jest macierzą kwadratową

• elementy na przekątnej są rzeczywiste.

Rzeczywista macierz hermitowska jest macierzą symetryczną.

Twierdzenie:

Jeżeli A jest macierzą zespoloną mxn to wówczas macierz jest macierzą hermitowską stopnia m.

Definicja:

Macierz A nazywamy antyhermitowską

(skośnie hermitowską) jeżeli zachodzi:

• Macierz hermitowska jest macierzą kwadratową .

• Jej elementy na przekątnej głównej są

czysto urojone lub zero.

Definicja :

Macierz A nazywamy unitarną jeżeli zachodzi:

Macierz unitarna jest macierzą kwadratową nieosobliwą

(det(A)
0). Elementy tej macierzy spełniają związek:

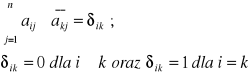
Algebra Liniowa z Geometrią

10

Y

P'(x',y')

θ

P(x,y)

Φ

X

---