
St. Kowalski, Wykłady z matematyki (dla studentów kierunku Mechanika) – wykład 2 – 8
1
Granica ci gu punktów.
Ci g punktów
)
(
n
P
,
)
;
(
n
n
n
y
x
P
=
, jest zbie ny do punktu
)
;
(
0
0
0
y
x
P
=
, gdy
0
)
(
)
(
lim
2
0
2
0
=
−
+
−
∞
→
y
y
x
x
n
n
n
.
Zatem
)
,
(
)
,
(
lim
lim
0
0
0
y
x
P
y
x
P
n
n
n
n
n
=
=
=
∞
→
∞
→
⇔
(
0
lim
x
x
n
n
=
∞
→
∧
0
lim
y
y
n
n
=
∞
→
)
[
1
]
Obliczymy granic ci gu
)
2
1
ln
,
(
)
,
(
+
+
=
n
n
n
y
x
n
n
n
.
Poniewa
1
lim
lim
=
=
∞
→
∞
→
n
n
n
n
n
x
,
0
1
ln
2
1
ln
lim
lim
=
=
+
+
=
∞
→
∞
→
n
n
y
n
n
n
, wi c ci g
)
2
1
ln
,
(
+
+
n
n
n
n
jest zbie ny i jego granic jest punkt
)
0
,
1
(
.
[
2
]
Obliczymy granic ci gu
)
2
cos
,
1
(sin
)
,
(
+
π
+
π
=
n
n
y
x
n
n
.
Poniewa
0
0
sin
1
sin
lim
lim
=
=
+
π
=
∞
→
∞
→
n
x
n
n
n
,
1
0
cos
2
cos
lim
lim
=
=
+
π
=
∞
→
∞
→
n
y
n
n
n
, wi c ci g
)
2
cos
,
1
(sin
+
π
+
π
n
n
jest zbie ny i jego
granic jest punkt
)
1
,
0
(
.
Zadania
1.
( )
(
)
(
)
n
n
a
n
n
n
n
ln
)
ln(
,
1
lim
1
−
+
−
−
∞
→
2.
( )
+
+
∞
→
2
1
2
,
cos
lim
2
2
n
n
n
k
n
n
n
3.
+
+
+
−
−
∞
→
n
n
n
n
n
n
n
n
,
1
4
3
2
lim
4
2
4.
−
−
+
∞
→
)
1
2
arctan(
,
arccos
lim
2
sin
n
n
n
n
n
n
Przykłady funkcji dwu zmiennych
Płaszczyzna niepionowa:
c
by
ax
z
+
+
=
.
Paraboloida eliptyczna:
2
2
2
2
b
y
a
x
z
+
=
.
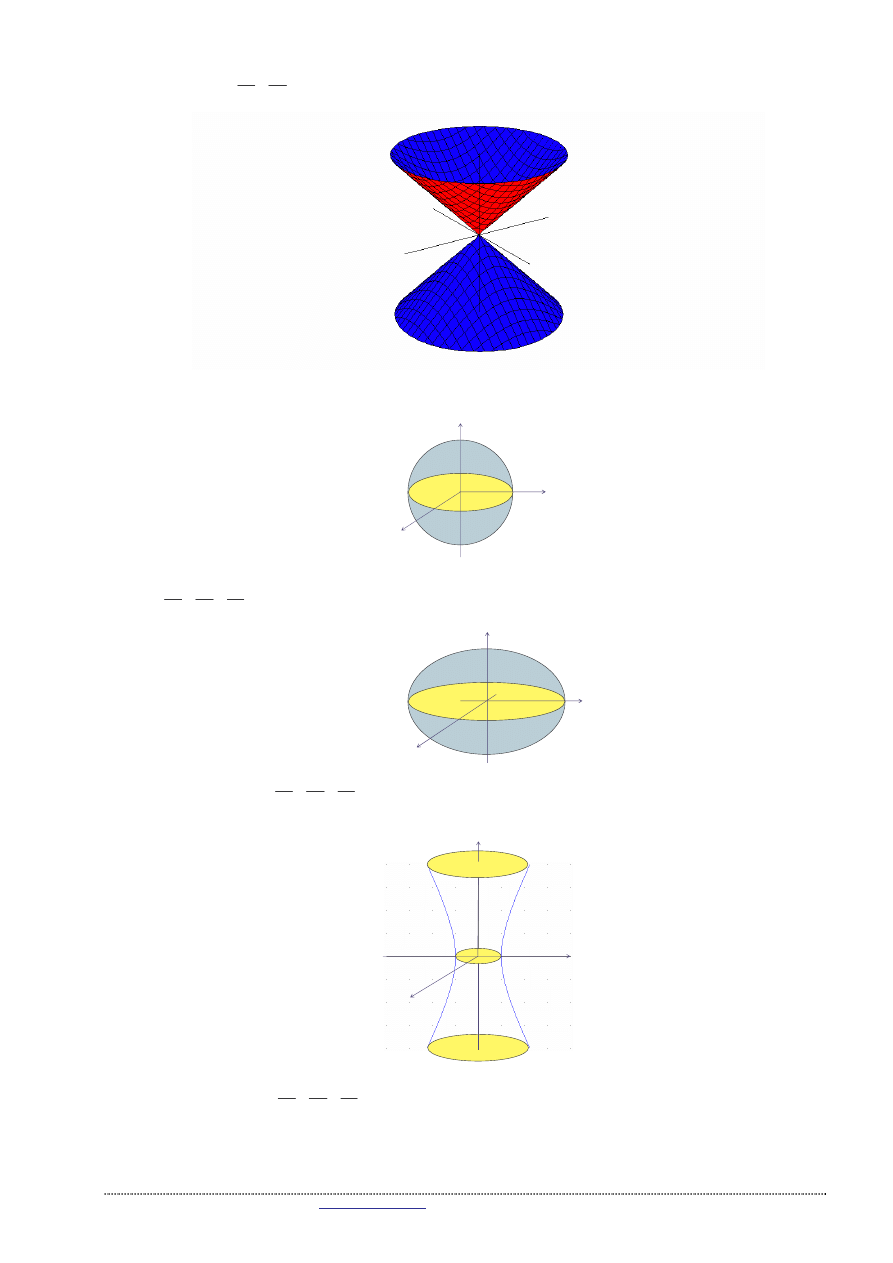
Sto ek eliptyczny – górna cz
:
2
2
2
2
b
y
a
x
z
+
=
.
St. Kowalski, Wykłady z matematyki (dla studentów kierunku Mechanika) – wykład 2 – 8
2
Sto ek eliptyczny:
2
2
2
2
2
b
y
a
x
z
+
=
(powierzchnia – nie jest funkcj ).
Sfera:
2
2
2
2
R
z
y
x
=
+
+
(powierzchnia – nie jest funkcj ).
Elipsoida:
1
2
2
2
2
2
2
=
+
+
c
z
b
y
a
x
(powierzchnia – nie jest funkcj ).
Hiperboloida jednopowłokowa:
1
2
2
2
2
2
2
=
−
+
c
z
b
y
a
x
(powierzchnia – nie jest funkcj ).
Hiperboloida dwupowłokowa:
1
2
2
2
2
2
2
=
+
−
−
c
z
b
y
a
x
(powierzchnia – nie jest funkcj ).

St. Kowalski, Wykłady z matematyki (dla studentów kierunku Mechanika) – wykład 2 – 8
3
Granica funkcji w punkcie skupienia jej dziedziny.
Definiujmy analogicznie jak dla funkcji jednej zmienne (wykład 5 – strona 3).
[
1
]
Obliczymy granic
2
2
2
2
)
0
,
0
(
)
,
(
1
1
lim
y
x
y
x
y
x
+
−
+
+
→
.
Rozwi zanie
Wyra enie w liczniku przekształcamy w oparciu o wzór
b
a
b
a
b
a
+
−
=
−
2
2
.
=
+
+
+
+
+
+
+
−
+
+
=
+
−
+
+
→
→
)
1
1
)(
(
)
1
1
)(
1
1
(
lim
1
1
lim
2
2
2
2
2
2
2
2
)
0
,
0
(
)
,
(
2
2
2
2
)
0
,
0
(
)
,
(
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
2
1
2
2
)
0
,
0
(
)
,
(
2
2
2
2
2
2
)
0
,
0
(
)
,
(
1
1
1
lim
)
1
1
)(
(
lim
=
+
+
+
=
+
+
+
+
+
=
→
→
y
x
y
x
y
x
y
x
y
x
y
x
.
[
2
]
Obliczymy granic
y
x
y
x
y
x
−
−
→
3
3
)
1
,
1
(
)
,
(
lim
.
3
)
(
lim
)
)(
(
lim
lim
2
2
)
1
,
1
(
)
,
(
2
2
)
1
,
1
(
)
,
(
3
3
)
1
,
1
(
)
,
(
=
+
+
=
−
+
+
−
=
−
−
→
→
→
y
xy
x
y
x
y
xy
x
y
x
y
x
y
x
y
x
y
x
y
x
[
3
]
Obliczy granic
+
→
xy
y
x
y
x
1
cos
)
(
lim
2
2
)
0
,
0
(
)
,
(
.
Korzystaj c z twierdzenia o trzech funkcjach poka emy, e
0
1
cos
)
(
lim
2
2
)
0
,
0
(
)
,
(
=
+
→
xy
y
x
y
x
.
Dla ka dego punktu
f
D
y
x
∈
)
,
(
słuszne s nierówno ci
2
2
2
2
2
2
1
cos
)
(
)
(
y
x
xy
y
x
y
x
+
≤
+
≤
+
−
. Poniewa
0
)
(
lim
2
2
)
0
,
0
(
)
,
(
=
−
−
→
y
x
y
x
,
0
)
(
lim
2
2
)
0
,
0
(
)
,
(
=
+
→
y
x
y
x
, wi c
0
1
cos
)
(
lim
2
2
)
0
,
0
(
)
,
(
=
+
→
xy
y
x
y
x
.
[
4
]
Obliczymy granic
2
2
2
2
)
0
,
0
(
)
,
(
lim
y
x
y
x
y
x
−
+
→
.
Poka emy, e granica ta nie istnieje. W tym celu rozpatrujemy dwa ci gi
=
′
′
0
,
1
)
,
(
n
y
x
n
n
,
=
′′
′′
n
y
x
n
n
1
,
0
)
,
(
zbie ne do punktu
)
0
,
0
(
oraz odpowiadaj ce im ci gi warto ci funkcji:
2
2
2
2
)
0
,
0
(
)
,
(
)
(
)
(
)
(
)
(
lim
n
n
n
n
y
x
y
x
y
x
n
n
′
−
′
′
+
′
→
′
′
1
0
1
0
1
lim
2
2
=
−
+
=
∞
→
n
n
n
,
2
2
2
2
)
0
,
0
(
)
,
(
)
(
)
(
)
(
)
(
lim
n
n
n
n
y
x
y
x
y
x
n
n
′′
−
′′
′′
+
′′
→
′′
′′
1
1
0
1
0
lim
2
2
−
=
−
+
=
∞
→
n
n
n
.
Otrzymali my ró ne granice cz ciowe, zatem rozwa ana granica nie istnieje.
St. Kowalski, Wykłady z matematyki (dla studentów kierunku Mechanika) – wykład 2 – 8
4
Zadania.
Uzasadni , e nie istnieje granica:
(1)
2
2
2
2
)
0
,
0
(
)
,
(
lim
y
xy
x
y
x
y
x
+
−
+
→
(2)
2
2
2
2
)
0
,
0
(
)
,
(
lim
y
x
y
x
y
x
+
−
→
(3)
2
2
)
0
,
0
(
)
,
(
3
lim
y
x
y
x
y
x
+
+
→
(4)
2
2
)
0
,
0
(
)
,
(
2
lim
y
x
xy
y
x
+
→
Obliczy granic :
(1)
2
2
2
2
)
0
,
0
(
)
,
(
4
16
lim
y
x
y
x
y
x
+
−
+
+
→
(2)
y
x
y
x
y
x
+
+
−
→
3
3
)
1
,
1
(
)
,
(
lim
(3)
xy
y
x
y
x
1
sin
)
(
lim
2
2
)
0
,
0
(
)
,
(
+
→
(4)
y
x
y
x
y
x
−
−
→
4
4
)
1
,
1
(
)
,
(
lim
Ci gło funkcji.
Definiujmy analogicznie jak dla funkcji jednej zmienne (wykład 6).
[1]
Czy mo na dobra warto
A
tak, by była ci gła funkcja
=
≠
−
+
+
+
=
?
)
0
,
0
(
)
,
(
dla
),
0
,
0
(
)
,
(
dla
1
1
)
,
(
2
2
2
2
y
x
A
y
x
y
x
y
x
y
x
f
=
−
+
+
+
=
=
→
1
1
lim
)
0
,
0
(
2
2
2
2
)
0
,
0
(
)
,
(
y
x
y
x
f
A
y
x
+
−
=
−
b
a
b
a
b
a
2
2
wzoru
ze
y
Skorzystam
=
−
+
+
+
+
+
+
=
→
1
)
1
(
)
1
1
)(
(
lim
2
2
2
2
2
2
)
0
,
0
(
)
,
(
y
x
y
x
y
x
y
x
2
)
1
1
(
lim
)
1
1
)(
(
lim
2
2
)
0
,
0
(
)
,
(
2
2
2
2
2
2
)
0
,
0
(
)
,
(
=
+
+
+
=
+
+
+
+
+
=
→
→
y
x
y
x
y
x
y
x
y
x
y
x
[2]
Czy mo na dobra warto
A
tak, by była ci gła funkcja
=
≠
+
−
+
+
=
).
0
,
0
(
)
,
(
dla
),
0
,
0
(
)
,
(
dla
1
1
)
,
(
2
2
2
2
y
x
A
y
x
y
x
y
x
y
x
f
2
1
2
2
2
2
)
0
,
0
(
)
,
(
1
1
lim
)
0
,
0
(
=
+
−
+
+
=
=
→
y
x
y
x
f
A
y
x
(przykład poprzedni)
[3]
Czy mo na dobra warto
A
tak, by była ci gła funkcja
=
≠
−
−
−
+
=
).
0
,
0
(
)
,
(
dla
),
0
,
0
(
)
,
(
dla
2
4
)
,
(
2
2
2
2
y
x
A
y
x
y
x
y
x
y
x
f
=
−
−
−
+
=
=
→
2
4
lim
)
0
,
0
(
2
2
2
2
)
0
,
0
(
)
,
(
y
x
y
x
f
A
y
x
.
+
−
=
−
b
a
b
a
b
a
2
2
wzoru
ze
y
Skorzystam
=
−
−
−
+
−
−
+
=
→
4
4
)
2
4
)(
(
lim
2
2
2
2
2
2
)
0
,
0
(
)
,
(
y
x
y
x
y
x
y
x
4
)
2
4
(
lim
)
(
)
2
4
)(
(
lim
2
2
)
0
,
0
(
)
,
(
2
2
2
2
2
2
)
0
,
0
(
)
,
(
−
=
+
−
−
−
=
+
−
+
−
−
+
=
→
→
y
x
y
x
y
x
y
x
y
x
y
x
[4]
Czy mo na dobra warto
A
tak, by była ci gła funkcja
=
≠
+
+
=
).
0
,
0
(
)
,
(
dla
),
0
,
0
(
)
,
(
dla
)
sin(
)
,
(
2
2
3
3
y
x
A
y
x
y
x
y
x
y
x
f
2
2
3
3
)
0
,
0
(
)
,
(
3
3
3
3
)
0
,
0
(
)
,
(
2
2
3
3
3
3
3
3
)
0
,
0
(
)
,
(
2
2
3
3
)
0
,
0
(
)
,
(
lim
)
sin(
lim
)
sin(
lim
)
sin(
lim
)
0
,
0
(
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
f
A
y
x
y
x
y
x
y
x
+
+
⋅
+
+
=
+
+
⋅
+
+
=
+
+
=
=
→
→
→
→
Mamy
1
)
sin(
lim
3
3
3
3
)
0
,
0
(
)
,
(
=
+
+
→
y
x
y
x
y
x
,
0
1
)
(
lim
)
)(
(
lim
lim
2
2
)
0
,
0
(
)
,
(
2
2
2
2
)
0
,
0
(
)
,
(
2
2
3
3
)
0
,
0
(
)
,
(
=
+
−
+
=
+
+
−
+
=
+
+
→
→
→
y
x
xy
y
x
y
x
y
xy
x
y
x
y
x
y
x
y
x
y
x
y
x
.
Dlatego
0
=
A
(gdy
2
3
2
2
2
1
1
≤
+
−
≤
y
x
xy
).

St. Kowalski, Wykłady z matematyki (dla studentów kierunku Mechanika) – wykład 2 – 8
5
•••
0
)
(
2
≥
+ y
x
→
0
2
2
2
≥
+
+
y
xy
x
→
xy
y
x
2
2
2
−
≥
+
→
2
2
2
1
y
x
xy
+
−
≥
→
2
2
2
1
y
x
xy
+
−
≥
→
2
2
2
3
1
y
x
xy
+
−
≥
0
)
(
2
≥
− y
x
→
0
2
2
2
≥
+
−
y
xy
x
→
xy
y
x
2
2
2
≥
+
→
2
2
2
1
y
x
xy
+
≥
→
2
2
2
1
y
x
xy
+
≥
→
2
2
2
1
y
x
xy
+
−
≤
−
→
2
2
2
1
1
y
x
xy
+
−
≤
•••
Zadania
Czy mo na dobra warto
A
tak, by poni sze funkcje były ci głe?
=
≠
−
+
+
+
=
).
0
,
0
(
)
,
(
dla
),
0
,
0
(
)
,
(
dla
1
1
)
,
(
2
2
2
2
1
y
x
A
y
x
y
x
y
x
y
x
f
=
≠
+
−
+
+
=
).
0
,
0
(
)
,
(
dla
),
0
,
0
(
)
,
(
dla
1
1
)
,
(
2
2
2
2
2
y
x
A
y
x
y
x
y
x
y
x
f
=
≠
+
−
+
=
).
0
,
0
(
)
,
(
dla
),
0
,
0
(
)
,
(
dla
1
1
)
,
(
2
2
2
2
3
y
x
A
y
x
y
x
y
x
y
x
f
=
≠
−
+
−
+
=
).
0
,
0
(
)
,
(
dla
),
0
,
0
(
)
,
(
dla
2
4
)
,
(
2
2
2
2
4
y
x
A
y
x
y
x
y
x
y
x
f
=
≠
+
+
=
).
0
,
0
(
)
,
(
dla
),
0
,
0
(
)
,
(
dla
)
sin(
)
,
(
2
2
3
3
5
y
x
A
y
x
y
x
y
x
y
x
f
=
≠
+
−
=
).
0
,
0
(
)
,
(
dla
),
0
,
0
(
)
,
(
dla
1
exp
)
,
(
2
2
6
y
x
A
y
x
y
x
y
x
f
(
)
=
≠
+
=
+
).
0
,
0
(
)
,
(
dla
),
0
,
0
(
)
,
(
dla
1
)
,
(
2
2
1
2
2
7
y
x
A
y
x
y
x
y
x
f
y
x
=
≠
+
=
).
0
,
0
(
)
,
(
dla
),
0
,
0
(
)
,
(
dla
|
|
)
,
(
2
2
8
y
x
A
y
x
y
x
xy
y
x
f
Pochodne cz stkowe.
x
y
x
f
y
x
x
f
y
x
f
y
x
x
x
x
f
∆
−
∆
+
=
=
→
∆
∂
∂
)
,
(
)
,
(
lim
)
,
(
)
,
(
0
0
0
0
0
0
0
0
0
y
y
x
f
y
y
x
f
y
x
f
y
x
y
y
y
f
∆
−
∆
+
=
=
→
∆
∂
∂
)
,
(
)
,
(
lim
)
,
(
)
,
(
0
0
0
0
0
0
0
0
0
[
Zad 1
]
Obliczymy pochodne cz stkowe (w dowolnym punkcie dziedziny) funkcji
32
3
)
,
(
6
2
3
−
+
=
y
x
xy
y
x
f
.
Pochodn cz stkow wzgl dem
x
liczymy tak jak zwykł pochodn funkcji jednej zmiennej
x
, przy czym zmienn
y
traktujemy jako stały
parametr:
6
3
2
6
3
6
)
(
3
)
(
)
,
(
xy
y
x
y
x
y
y
x
f
x
x
x
+
=
+
=
∂
∂
∂
∂
.
Pochodn cz stkow wzgl dem
y
liczymy tak jak zwykł pochodn funkcji jednej zmiennej
y
, przy czym zmienn
x
traktujemy jako stały
parametr:
5
2
2
6
2
3
16
3
)
(
3
)
(
)
,
(
y
x
xy
y
x
y
x
y
x
f
y
y
y
+
=
+
=
∂
∂
∂
∂
.
[
Zad 2
]
Obliczy pochodne cz stkowe (w dowolnym punkcie dziedziny) funkcji
3
4
3
)
,
(
6
2
3
−
−
+
−
=
y
x
y
x
y
x
f
.
x
y
x
f
x
6
1
)
,
(
+
=
,
5
2
24
3
)
,
(
y
y
y
x
f
y
−
−
=
.
[
Zad 3
]
Obliczy pochodne cz stkowe (w dowolnym punkcie dziedziny) funkcji
x
y
y
x
y
x
f
+
=
)
,
(
.
2
2
1
1
1
1
)
(
1
)
,
(
x
x
y
x
y
y
x
y
x
y
y
x
f
x
x
x
−
=
−
⋅
+
=
⋅
+
′
⋅
=
∂
∂
,
St. Kowalski, Wykłady z matematyki (dla studentów kierunku Mechanika) – wykład 2 – 8
6
x
y
x
x
y
x
y
x
y
x
y
x
f
y
y
y
1
1
1
)
(
1
1
)
,
(
2
2
+
−
=
+
−
=
⋅
+
⋅
=
∂
∂
∂
∂
.
[
Zad 4
]
Obliczymy pochodne cz stkowe (w dowolnym punkcie dziedziny) funkcji
2
2
9
4
)
,
(
y
x
y
x
f
+
=
.
2
2
2
2
4
2
8
)
,
(
y
x
x
y
x
x
y
x
f
x
+
=
+
=
dla
)
0
,
0
(
)
,
(
≠
y
x
.
x
x
x
x
x
f
x
f
f
x
x
x
x
∆
∆
=
∆
−
∆
=
∆
−
∆
+
=
→
∆
→
∆
→
∆
|
|
2
lim
0
)
(
4
lim
)
0
,
0
(
)
0
,
0
(
lim
)
0
,
0
(
0
2
0
0
nie istnieje (granice jednostronne s ró ne).
2
2
2
2
9
2
18
)
,
(
y
x
y
y
x
y
y
x
f
y
+
=
+
=
dla
)
0
,
0
(
)
,
(
≠
y
x
.
y
y
y
y
y
f
y
f
f
y
y
y
y
∆
∆
=
∆
−
∆
=
∆
−
∆
+
=
→
∆
→
∆
→
∆
|
|
3
lim
0
)
(
9
lim
)
0
,
0
(
)
0
,
0
(
lim
)
0
,
0
(
0
2
0
0
nie istnieje (granice jednostronne s ró ne).
[
Zad 5
]
Obliczymy pochodne cz stkowe (w dowolnym punkcie dziedziny) funkcji
4
2
9
4
)
,
(
y
x
y
x
f
+
=
.
4
2
4
2
4
2
8
)
,
(
y
x
x
y
x
x
y
x
f
x
+
=
+
=
dla
)
0
,
0
(
)
,
(
≠
y
x
.
x
x
x
x
x
f
x
f
f
x
x
x
x
∆
∆
=
∆
−
∆
=
∆
−
∆
+
=
→
∆
→
∆
→
∆
|
|
2
lim
0
)
(
4
lim
)
0
,
0
(
)
0
,
0
(
lim
)
0
,
0
(
0
2
0
0
nie istnieje..
4
2
3
4
2
3
9
2
18
)
,
(
y
x
y
y
x
y
y
x
f
y
+
=
+
=
dla
)
0
,
0
(
)
,
(
≠
y
x
.
0
3
lim
)
(
3
lim
0
)
(
9
lim
)
0
,
0
(
)
0
,
0
(
lim
)
0
,
0
(
0
2
0
4
0
0
=
∆
=
∆
∆
=
∆
−
∆
=
∆
−
∆
+
=
→
∆
→
∆
→
∆
→
∆
y
y
y
y
y
y
f
y
f
f
y
y
y
y
y
.
[
Zad 6
]
Obliczymy pochodne cz stkowe (w dowolnym punkcie dziedziny) funkcji
3
3
3
)
,
(
y
x
y
x
f
+
=
.
3
2
3
3
2
3
2
3
3
2
)
(
)
(
3
3
)
,
(
y
x
x
y
x
x
y
x
f
x
+
=
+
=
dla
)
0
,
0
(
)
,
(
≠
y
x
1
lim
0
)
(
lim
)
0
,
0
(
)
0
,
0
(
lim
)
0
,
0
(
0
3
3
0
0
=
∆
∆
=
∆
−
∆
=
∆
−
∆
+
=
→
∆
→
∆
→
∆
x
x
x
x
x
f
x
f
f
x
x
x
x
,
3
2
3
3
2
3
2
3
3
2
)
(
)
(
3
3
)
,
(
y
x
y
y
x
y
y
x
f
y
+
=
+
=
dla
)
0
,
0
(
)
,
(
≠
y
x
1
lim
0
)
(
lim
)
0
,
0
(
)
0
,
0
(
lim
)
0
,
0
(
0
3
3
0
0
=
∆
∆
=
∆
−
∆
=
∆
−
∆
+
=
→
∆
→
∆
→
∆
y
y
y
y
y
f
y
f
f
y
y
y
y
.
[
Zad 7
]
Obliczymy pochodne cz stkowe (w dowolnym punkcie dziedziny) funkcji
x
y
y
x
y
x
f
cos
sin
)
,
(
⋅
=
.
Zastosujemy wzór na pochodn iloczynu funkcji.
( )
( )
( )
x
y
y
x
x
y
x
y
y
x
y
x
y
x
y
x
x
y
y
x
x
y
x
x
y
x
y
x
x
y
y
x
x
x
f
y
x
sin
sin
cos
cos
sin
sin
cos
)
(
cos
cos
sin
cos
sin
)
,
(
2
1
⋅
−
⋅
=
⋅
−
⋅
⋅
=
⋅
+
⋅
=
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
( )
( )
( )
( )
x
y
y
x
x
x
y
y
x
y
x
x
y
x
y
y
y
x
x
y
y
x
y
y
x
x
y
y
y
x
x
y
y
x
y
y
f
y
x
sin
sin
cos
cos
sin
sin
cos
cos
cos
sin
cos
sin
)
,
(
1
2
⋅
−
⋅
−
=
⋅
⋅
−
⋅
⋅
=
⋅
+
⋅
=
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
[
Zad 8
]
Obliczymy pochodne cz stkowe funkcji
2
2
9
)
3
2
(
arcsin
)
,
(
y
x
x
y
x
f
−
−
+
−
=
.
2
2
2
2
2
2
9
)
3
2
(
1
2
2
2
9
2
1
)
3
2
(
1
1
2
2
)
9
(
)
3
2
(
9
)
3
2
(
arcsin
)
,
(
y
x
x
x
x
y
x
x
x
x
x
f
y
x
x
y
x
x
y
x
−
−
−
−
∂
∂
−
−
∂
∂
−
−
∂
∂
∂
∂
−
=
−
−
⋅
+
−
⋅
=
−
−
+
−
=
2
2
2
2
9
2
2
9
2
1
2
2
)
9
(
9
)
3
2
(
arcsin
)
,
(
y
x
y
y
y
x
y
y
f
y
x
y
x
x
y
x
−
−
∂
∂
−
−
∂
∂
∂
∂
−
=
−
−
⋅
=
−
−
+
−
=
[
Zad 9
]
Dana jest funkcja
≠
=
=
.
0
dla
1
,
0
dla
0
)
,
(
xy
xy
y
x
f
Czy funkcja
f
jest ci gła w punkcie
O
(0,0)? Obliczy
)
0
,
0
(
x
f
i
)
0
,
0
(
y
f
.
St. Kowalski, Wykłady z matematyki (dla studentów kierunku Mechanika) – wykład 2 – 8
7
Funkcja nie jest ci gła w punkcie
O
(0,0), gdy nie ma granicy w tym punkcie. Aby to uzasadni wystarczy wzi dwa ci gi punktów zbie ne
do punktu
O
(0,0), dla których odpowiadaj ce im ci gi warto ci funkcji b d miały ró ne granice. Dla ci gów
)
0
,
(
)
,
(
1
n
n
n
y
x
=
′
′
,
)
,
(
)
,
(
1
1
n
n
n
n
y
x
=
′′
′′
mamy
0
)
,
(
lim
)
0
,
0
(
)
,
(
=
′
′
→
′
′
n
n
y
x
y
x
f
n
n
,
1
)
,
(
lim
)
0
,
0
(
)
,
(
=
′′
′′
→
′′
′′
y
x
f
n
y
x
n
n
.
Otrzymali my ró ne granice, zatem granica funkcji w punkcie
O
(0,0) nie istnieje.
Pochodne cz stkowe
)
0
,
0
(
x
f
i
)
0
,
0
(
y
f
b dziemy wylicza na podstawie definicji.
0
0
0
lim
)
0
,
0
(
)
0
,
0
(
lim
)
0
,
0
(
0
0
=
∆
−
=
∆
−
∆
+
=
→
∆
→
∆
x
x
f
x
f
f
x
x
x
,
0
0
0
lim
)
0
,
0
(
)
0
,
0
(
lim
)
0
,
0
(
0
0
=
∆
−
=
∆
−
∆
+
=
→
∆
→
∆
y
y
f
y
f
f
y
y
y
.
Z tego przykładu wynika, e nawet nieci głe w punkcie funkcje mog mie obie pochodne cz stkowe w tym punkcie.
Ró niczkowalno
Funkcja jest ró niczkowalna w punkcie
)
,
(
0
0
y
x
wtedy i tylko wtedy, gdy
0
)
(
)
(
)
(
)
,
(
)
(
)
,
(
)
,
(
)
,
(
lim
2
0
2
0
0
0
0
0
0
0
0
0
)
,
(
)
,
(
0
0
=
−
+
−
−
⋅
∂
∂
−
−
⋅
∂
∂
−
−
→
y
y
x
x
y
y
y
x
y
f
x
x
y
x
x
f
y
x
f
y
x
f
y
x
y
x
.
Ró niczkowalno funkcji
f
w punkcie
)
,
(
0
0
y
x
oznacza, e istnieje niepionowa płaszczyzna styczna do wykresu tej funkcji w punkcie
)
)
,
(
,
,
(
0
0
0
0
y
x
f
y
x
Równanie płaszczyzny stycznej w punkcie
)
)
,
(
,
,
(
0
0
0
0
y
x
f
y
x
do wykresu funkcji ró niczkowalnej
)
,
( y
x
f
z
=
ma posta
)
(
)
,
(
)
(
)
,
(
)
,
(
0
0
0
0
0
0
0
0
y
y
y
x
y
f
x
x
y
x
x
f
y
x
f
z
−
⋅
∂
∂
+
−
⋅
∂
∂
=
−
Zadanie 1.
Funkcja
≠
=
=
.
0
dla
1
,
0
dla
0
)
,
(
xy
xy
y
x
f
ma pochodne cz stkowe w punkcie
O
(0,0). Czy jest ró niczkowalna w punkcie
O
(0,0)?
Rozwi zanie
Funkcja nie jest ci gła w punkcie
O
(0,0) (gdy nie ma granicy w tym punkcie), zatem nie spełnia warunku koniecznego ró niczkowalno ci.
Zadanie 2.
Czy funkcja
xy
y
x
f
=
)
,
(
jest ró niczkowalna w punkcie
O
(0,0)?
Rozwi zanie
Przypominamy, e na mocy definicji, funkcja jest ró niczkowalna w punkcie
)
,
(
0
0
y
x
wtedy i tylko wtedy, gdy
0
)
(
)
(
)
(
)
,
(
)
(
)
,
(
)
,
(
)
,
(
lim
2
0
2
0
0
0
0
0
0
0
0
0
)
,
(
)
,
(
0
0
=
−
+
−
−
⋅
∂
∂
−
−
⋅
∂
∂
−
−
→
y
y
x
x
y
y
y
x
y
f
x
x
y
x
x
f
y
x
f
y
x
f
y
x
y
x
.
Poniewa
0
0
0
lim
)
0
,
0
(
)
0
,
0
(
lim
)
0
,
0
(
0
0
=
∆
−
=
∆
−
∆
+
=
→
∆
→
∆
x
x
f
x
f
f
x
x
x
,
0
0
0
lim
)
0
,
0
(
)
0
,
0
(
lim
)
0
,
0
(
0
0
=
∆
−
=
∆
−
∆
+
=
→
∆
→
∆
y
y
f
y
f
f
y
y
y
,
wi c
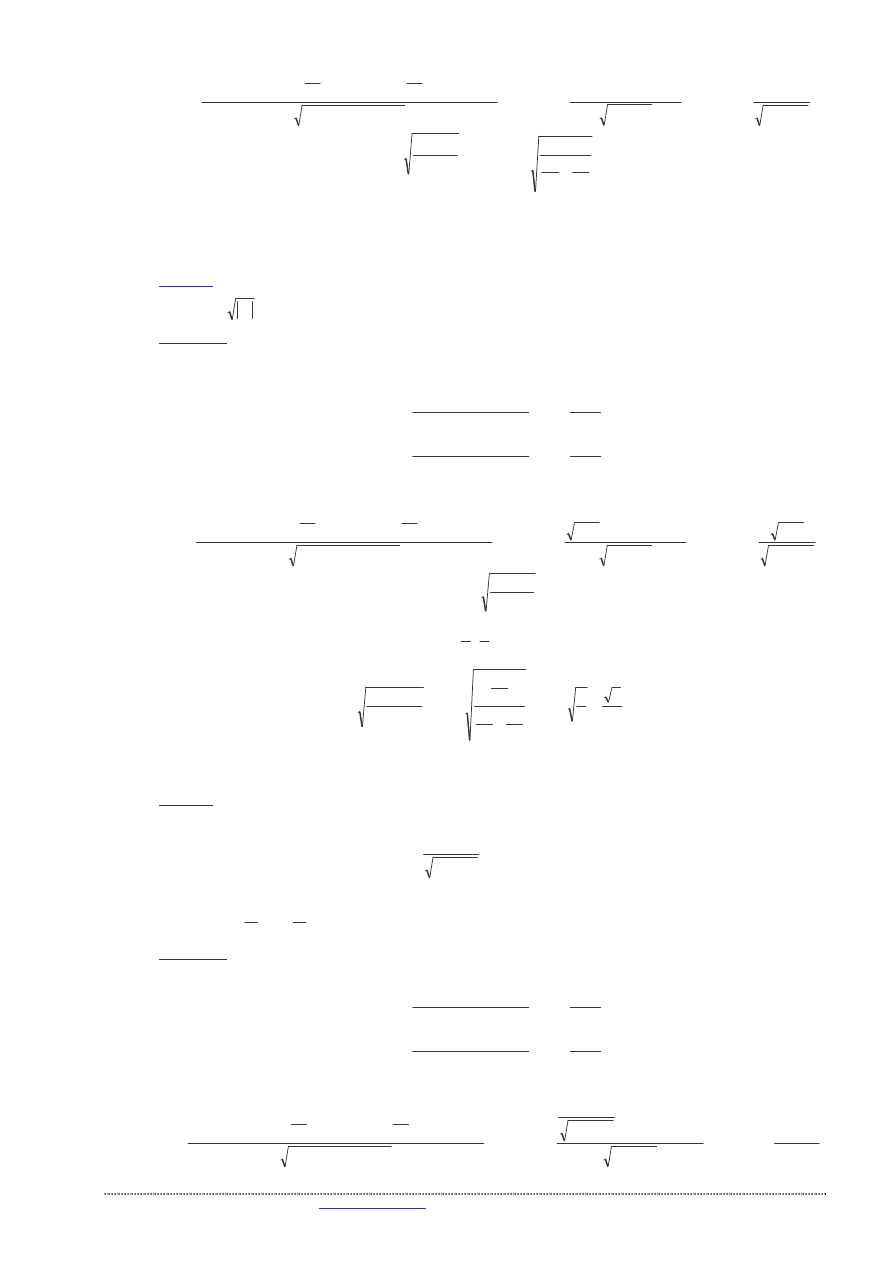
St. Kowalski, Wykłady z matematyki (dla studentów kierunku Mechanika) – wykład 2 – 8
8
=
−
+
−
−
⋅
∂
∂
−
−
⋅
∂
∂
−
−
→
2
2
)
0
,
0
(
)
,
(
)
0
(
)
0
(
)
0
(
)
0
,
0
(
)
0
(
)
0
,
0
(
)
0
,
0
(
)
,
(
lim
y
x
y
y
f
x
x
f
f
y
x
f
y
x
=
+
⋅
−
⋅
−
−
→
2
2
)
0
,
0
(
)
,
(
0
0
0
|
|
lim
y
x
y
x
xy
y
x
2
2
)
0
,
0
(
)
,
(
|
|
lim
y
x
xy
y
x
+
→
2
2
2
2
)
0
,
0
(
)
,
(
lim
y
x
y
x
y
x
+
=
→
0
1
1
1
lim
2
2
)
0
,
0
(
)
,
(
=
+
=
→
x
y
y
x
.
Dlatego funkcja jest ró niczkowalna w punkcie
O
(0,0). Macierz Jacobiego funkcji
f
w punkcie
O
(0,0) jest
(
)
[ ]
0
0
)
0
,
0
(
)
0
,
0
(
)
0
,
0
(
=
=
′
y
x
f
f
f
.
Zadanie 3.
Czy funkcja
xy
y
x
f
=
)
,
(
jest ró niczkowalna w punkcie
O
(0,0)?
Rozwi zanie
Skorzystamy z definicji funkcji ró niczkowalnej w punkcie
O
(0,0).
Poniewa
0
0
0
lim
)
0
,
0
(
)
0
,
0
(
lim
)
0
,
0
(
0
0
=
∆
−
=
∆
−
∆
+
=
→
∆
→
∆
x
x
f
x
f
f
x
x
x
,
0
0
0
lim
)
0
,
0
(
)
0
,
0
(
lim
)
0
,
0
(
0
0
=
∆
−
=
∆
−
∆
+
=
→
∆
→
∆
y
y
f
y
f
f
y
y
y
,
wi c
=
−
+
−
−
⋅
∂
∂
−
−
⋅
∂
∂
−
−
→
2
2
)
0
,
0
(
)
,
(
)
0
(
)
0
(
)
0
(
)
0
,
0
(
)
0
(
)
0
,
0
(
)
0
,
0
(
)
,
(
lim
y
x
y
y
f
x
x
f
f
y
x
f
y
x
=
+
⋅
−
⋅
−
−
→
2
2
)
0
,
0
(
)
,
(
0
0
0
|
|
lim
y
x
y
x
xy
y
x
2
2
)
0
,
0
(
)
,
(
|
|
lim
y
x
xy
y
x
+
→
2
2
)
0
,
0
(
)
,
(
|
|
lim
y
x
xy
y
x
+
=
→
.
Poka emy, e ostatnia granica nie jest równa 0. Niech
)
1
,
1
(
)
,
(
n
n
y
x
n
n
=
. Wówczas
2
2
2
1
lim
1
1
1
lim
lim
2
2
2
2
2
=
=
+
=
+
∞
→
∞
→
∞
→
n
n
n
n
n
n
n
n
n
n
y
x
y
x
.
Dlatego funkcja nie jest ró niczkowalna w punkcie
O
(0,0).
Zadanie 4.
Sprawdzi , e funkcja
=
≠
+
=
),
0
,
0
(
)
,
(
dla
0
),
0
,
0
(
)
,
(
dla
)
,
(
2
2
y
x
y
x
y
x
xy
y
x
f
ma pochodne cz stkowe
)
0
,
0
(
x
f
∂
∂
,
)
0
,
0
(
y
f
∂
∂
, ale nie jest ró niczkowalna w punkcie (0,0).
Rozwi zanie
Mamy
0
0
0
lim
)
0
,
0
(
)
0
,
0
(
lim
)
0
,
0
(
0
0
=
∆
−
=
∆
−
∆
+
=
→
∆
→
∆
x
x
f
x
f
f
x
x
x
,
0
0
0
lim
)
0
,
0
(
)
0
,
0
(
lim
)
0
,
0
(
0
0
=
∆
−
=
∆
−
∆
+
=
→
∆
→
∆
y
y
f
y
f
f
y
y
y
.
Dlatego
=
−
+
−
−
⋅
∂
∂
−
−
⋅
∂
∂
−
−
→
2
2
)
0
,
0
(
)
,
(
)
0
(
)
0
(
)
0
(
)
0
,
0
(
)
0
(
)
0
,
0
(
)
0
,
0
(
)
,
(
lim
y
x
y
y
f
x
x
f
f
y
x
f
y
x
2
2
2
2
)
0
,
0
(
)
,
(
0
0
0
lim
y
x
y
x
y
x
xy
y
x
+
⋅
−
⋅
−
−
+
→
2
2
)
0
,
0
(
)
,
(
lim
y
x
xy
y
x
+
=
→
.

St. Kowalski, Wykłady z matematyki (dla studentów kierunku Mechanika) – wykład 2 – 8
9
Poka emy, e ostatnia granica nie jest równa 0. Niech
)
1
,
1
(
)
,
(
n
n
y
x
n
n
=
. Wówczas
2
1
2
1
lim
1
1
1
lim
lim
2
2
2
2
2
=
=
+
=
+
∞
→
∞
→
∞
→
n
n
n
n
n
n
n
n
n
n
y
x
y
x
.
Dlatego funkcja nie jest ró niczkowalna w punkcie
O
(0,0).
Zadanie 5.
Sprawdzi , e funkcja
=
≠
+
⋅
+
=
),
0
,
0
(
)
,
(
dla
0
),
0
,
0
(
)
,
(
dla
1
sin
)
(
)
,
(
2
2
2
2
y
x
y
x
y
x
y
x
y
x
f
ma nieci głe pochodne cz stkowe w punkcie
O
(0,0). Sprawd to! Jest jednak w tym punkcie ró niczkowalna.
Zadanie 6.
Czy jest ró niczkowalna w punkcie
O
(0,0) funkcja
=
≠
=
+
−
).
0
,
0
(
)
,
(
dla
0
),
0
,
0
(
)
,
(
dla
)
,
(
2
2
1
y
x
y
x
e
y
x
f
y
x
Wyszukiwarka
Podobne podstrony:
funkcje wielu zmiennych zadania od Misiaka id 182151
Funkcje zmiennej zespolonej id Nieznany
AM2 4 Funkcje wielu zmiennych i Nieznany (2)
AM2 5 Funkcje wielu zmiennych Ciag Dalszy id 58808 (2)
C 04,5 Rachunek różniczkowy funkcji wielu zmiennych
10 Funkcje wielu zmiennych
Matematyka III (Ćw) Lista 06 Ekstrema lokalne i globalne funkcji wielu zmiennych Zadania
11 RACHUNEK RÓŻNICZKOWY FUNKCJI WIELU ZMIENNYCH
ek mat ii optymalizacja funkcji wielu zmiennych
140 Funkcje wielu zmiennych
04 Rozdział 02 Różniczkowanie funkcji wielu zmiennych
7 Funkcje wielu zmiennych
wykład 3 funkcje wielu zmiennych
11 3 Funkcje wielu zmiennych
11 4 Funkcje wielu zmiennych
15 Funkcje wielu zmiennychid 16138
Funkcje wielu zmiennych 3
więcej podobnych podstron