ANALIZA MATEMATYCZNA II

A. Całka krzywoliniowa niezorientowana z pola skalarnego ciągłego
, po łuku regularnym
o opisie parametrycznym
dla
wyraża się wzorem

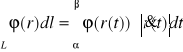
lub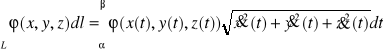
gdzie:
wektor styczny do łuku w punkcie
. Gdy łuk płaski
jest dany w postaci wykresu funkcji klasy
np:
dla
to wektor styczny do łuku w punkcie
ma postać
i całka krzywoliniowa po tym łuku wyraża się wzorem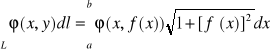
. Długość łuku regularnego
o opisie parametrycznym
dla
wyraża się wzorem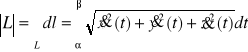
. Współrzędne środka ciężkości jednorodnego łuku regularnego
są określone wzorami: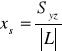
;
;
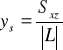
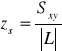
; gdzie:
;
;
; 1.Obliczyć całki krzywoliniowe niezorientowane po wskazanych łukach a)
gdzie
brzeg trójkąta o wierzch.
,
,
. Odp:
b)
, gdzie
okrąg o równaniu
. Odp:
c)
, gdzie
odcinek łączący punkty
i
. Odp:
d)
, gdzie
okrąg o równaniu
i
. Odp:
e*)
, gdzie
okrąg powstały z przecięcia sfery o równaniu
i płaszczyzny o równaniu
. Odp:
f*)
, gdzie
jest częścią wspólną powierzchni stożka
i walca równaniu
. Odp:
2. Obliczyć długość łuku krzywej
o opisie parametrycznym a)
dla
i
(wycinek cykloidy) Odp:
b)
dla
i
(wycinek linii śrubowej) Odp:
c)
dla
i (wycinek spirali) Odp:

3. Obliczyć współrzędne środków ciężkości danych jednorodnych łuków: a) wycinka linii śrubowej
dla
Odp:
b)wycinka linii łańcuchowej
dla
Odp: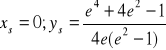
. c) brzeg trójkąta sferycznego
dla
. Odp:
. B. Całka krzywoliniowa zorientowana z pola wektorowego ciągłego
po łuku
regularnym zorientowanym o opisie parametrycznym
dla
zgodnym z orientacją łuku
wyraża się wzorem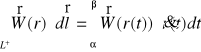
lub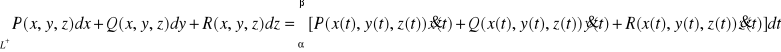
Gdy łuk płaski
jest dany w postaci wykresu funkcji klasy
np:
dla
to wektor styczny do łuku w punkcie
ma postać
i całka krzywo- liniowa zorientowana po tym łuku wyraża się wzorem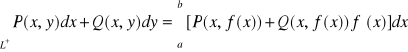
1.Obliczyć całki krzywoliniowe zorientowane po wskazanych łukach o orientacji zgodnej z parametryzacją a)
gdzie

dla
(wycinek paraboli) Odp:
b)
gdzie

dla
(wycinek elipsy) Odp:
c)
gdzie

dla
. Odp:
d)
gdzie

dla
Odp:
e)
gdzie
odcinek o początku
i końcu
Odp:
f*)
gdzie
jest krzywą powstałą z przecięcia górnej powierzchni sfery
i walca
Odp:
. 2.Obliczyć całki krzywoliniowe zorientowane po wskazanych łukach o orientacji zgodnej z parametryzacją a)
gdzie
jest brzegiem trójkąta o wierzchołkach
,
,
zorientowanym dodatnio względem wnętrza. Odp:
. b)
gdzie
jest okręgiem
zorientowanym dodatnio względem wnętrza. Odp:
c)
gdzie
jest brzegiem trójkąta o wierzchołkach
,
,
zorientowanym
Odp:

3.Obliczyć pracę w podanych polach sił po wskazanych łukach zorientowanych a)
gdzie
jest odcinkiem o początku w punkcie
i końcu w punkcie
. Odp:
b)
gdzie
jest łukiem
o początku w punkcie
i końcu w punkcie
. Odp:
c)
gdzie
odcinek o początku
i końcu
Odp:

C. Niech pole wektorowe
będzie klasy
w obszarze
, którego brzegiem jest krzywa regularna zamknięta
zorientowana dodatnio względem wnętrza, tego obszaru to wtedy zachodzi wzór Greena
Korzystając ze wzoru Greena obliczyć podane całki krzywoliniowe po brzegach
dodatnio zorientowanych względem wnętrza obszaru

a)
gdzie
jest brzegiem obszaru
ograniczonego krzywymi
i
. Odp:
b)
gdzie
jest brzegiem obszaru
Odp:
c)
gdzie
jest brzegiem obszaru
Odp:
d)
gdzie
jest brzegiem obszaru trójkąta
o wierzchołkach
,
,
. Odp:
e)
gdzie
jest brzegiem obszaru
Odp:

Całki powierzchniowe: A. Całka powierzchniowa niezorientowana z pola skalarnego ciągłego
, po płacie regularnym
o opisie parametrycznym
dla
wyraża się wzorem:

gdzie:
wektor normalny do płata w punkcie
Gdy płat
jest dany w postaci wykresu funkcji klasy
np:
dla
to wektor normalny do płata
w punkcie

1.Obliczyć całki powierzchniowe niezorientowane po wskazanych płatach: a)
gdzie
część stożka
odciętego płaszczyznami
i
b)
gdzie
część płaszczyzny
zawartej w pierwszym oktancie. c)
gdzie
część sfery
odciętej płaszczyznami
i
d)
gdzie
część walca
odciętego płaszczyznami
i

e)
gdzie
część powierzchni
odciętej płaszczyznami
i
Odp: a)
; b)
; c)
; d)
; e)
. 2. Obliczyć pola powierzchni podanych płatów a)
część płaszczyzny
zawartej w walcu
b)
część paraboloidy
odciętej płaszczyzną
c)
część stożka
odciętego płaszczyznami
i

Odp: a)
; b)
; c)
; 3. Obliczyć współrzędne środka ciężkości jednorodnych podanych płatów a)
część płaszczyzny
zawartej w walcu
b)
część paraboloidy
odciętej płaszczyzną
c)
część stożka
odciętego płaszczyznami
i
. Odp: a)
; b)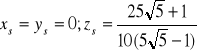
; c)
. B. Całka powierzchniowa zorientowana z pola wektorowego ciągłego
, po płacie regularnym zorientowanym
o opisie parametrycznym
dla
zgodnym z orientacją płata
wyraża się wzorem

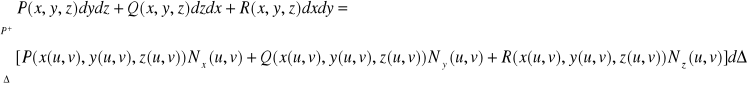
gdzie:
wektor normalny do płata w punkcie
Gdy płat
jest dany w postaci wykresu funkcji klasy
np:
dla
to
wektor normalny do płata w punkcie

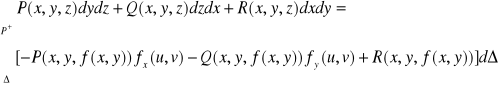
1.Obliczyć całki powierzchniowe zorientowane po wskazanych płatach: a)
gdzie
górna część paraboloidy
odciętej płaszczyzną
. Odp:
. b)
gdzie
dolna część płaszczyzny
zawarta w pierwszym oktancie. Odp:
. c)
gdzie
zewnętrzna strona części walca
odciętego płaszczyznami
i
. Odp:
. d)
gdzie
górna część paraboloidy
odciętej płaszczyznami
i
,
. Odp:
. e)
gdzie
jest zewnętrzną stroną powierzchni sfery
. Odp:
.

C. Niech pole wektorowe będzie
będzie klasy
w obszarze
, którego brzegiem jest powierzchnia regularna zamknięta
zorientowana zewnętrznie, wtedy zachodzi wzór Gaussa

Niech pole wektorowe będzie
będzie polem prędkości cieczy na powierzchni zorientowanej
, wtedy strumień cieczy wypływającej przez tę powierzchnie w jednostce czasu w kierunku zgodnym z orientacją wyraża się wzorem
. 1.Korzystając ze wzoru Gaussa obliczyć całki powierzchniowe zorientowane po danych powierzchniach zorientowanych. Sprawdzić otrzymane wyniki obliczając całki bezpośrednio. a)
gdzie
jest zewnętrzną stroną brzegu obszaru
ograniczonego sferą
. b)
gdzie
jest zewnętrzną stroną brzegu obszaru
ograniczonego walcem
oraz płaszczyznami
i
.

c)
gdzie
jest zewnętrzną stroną brzegu obszaru
ograniczonego stożkiem
i płaszczyzną
. Odp: a)
; b)
; c)
.

2.Obliczyć strumienie podanych pól wektorowych przez podane powierzchnie: a)
gdzie
jest zewnętrzną całkowitą powierzchnią walca
i
. Odp:
. b)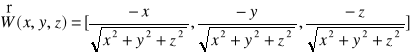
gdzie
jest powierzchnią zewnętrzną sfery
. Odp:
.

c)
gdzie
jest górną częścią płaszczyzny
odciętą płaszczyznami układu współrzędnych. Odp:
.

---