.::ZestaW III::.
Znaleźć połączenie i przecięcie rodziny zbiorów:
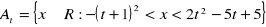
, gdzie
a)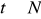
b)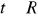
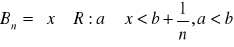
, gdzie
a)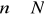
Niech
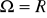
, A=[0,4], B=[1,2[ Podać wszystkie elementy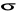
- algebry generowanej przez {A,B}
Dane są dwie różne
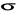
- algebry U1 i U2 na Ω. Sprawdzić czy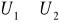
jest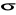
- algebrą na Ω.
Niech
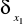
i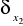
oznaczają miary Diraca na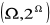
. Dla jakich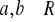
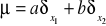
jest miarą, a dla jakich jest prawdopodobieństwem ?
Niech
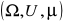
- przestrzeń z miarą. Pokazać, że:
1o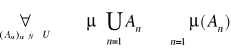
2o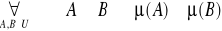
3o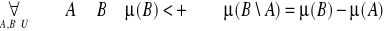
Udowodnić, że:
1o l([a,b]) = l([a,b[) = b - a
2o l({a}) = 0
3o l(N) = 0
4o l([0,1]\Q) = 1 oraz l([0,1]∩Q) = 0
Niech
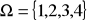
,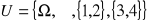
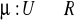
;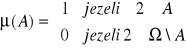
a) sprawdzić, czy U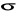
- algebra
b) sprawdzić, czy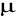
jest miarą ?, czy zupełną ?, czy unormowaną ?
c) uzupełnić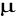
do miary zupełnej
Obliczyć:
1o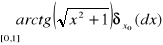
jeżeli:
a) xo = 0
b) xo = 4
2o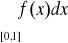
, jeżeli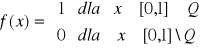
3o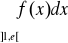
, jeżeli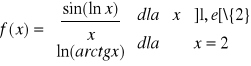
Niech
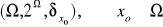
będzie przestrzeń z miarą,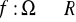
- odwzorowaniem.
Udowodnić, że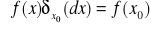
Wyszukiwarka
Podobne podstrony:
Zestaw II, Psychologia, biologia, Matematyka
Zestaw VI, Psychologia, biologia, Matematyka
Zestaw II, Psychologia, biologia, Matematyka
Zestaw V, Psychologia, biologia, Matematyka
Wyklad25, Psychologia, biologia, Matematyka
Wyklad22, Psychologia, biologia, Matematyka
Wyklad14, Psychologia, biologia, Matematyka
Wyklad26, Psychologia, biologia, Matematyka
Wyklad18, Psychologia, biologia, Matematyka
Wyklad28, Psychologia, biologia, Matematyka
Wyklad23, Psychologia, biologia, Matematyka
Wyklad27, Psychologia, biologia, Matematyka
Wyklad11, Psychologia, biologia, Matematyka
Wyklad24, Psychologia, biologia, Matematyka
zagadnienia(1), Psychologia, biologia, Matematyka
Wyklad15, Psychologia, biologia, Matematyka
Wyklad21, Psychologia, biologia, Matematyka
Wyklad4(1), Psychologia, biologia, Matematyka
Wyklad8(1), Psychologia, biologia, Matematyka
więcej podobnych podstron