ESTYMACJA STATYSTYCZNA (duża próba)

W celu zbadania średnich wysokości sumy ubezpieczenia na życie wylosowano potencjalnych klientów firmy ubezpieczeniowej i na podstawie tej próby uzyskano następujące wyniki :

Suma ubezp. (w tyś zł)	L. klientów Ni	Środki przedział. X	Nisk.
10-20	70	15	70
20-30	85	25	155
30-40	110	35	265
40-50	90	45	355
50-60	60	55	415
Razem	415	x	x

1. Zbadaj przeciętny poziom, dyspersje oraz asymetrię w próbie

1. Oblicz średnią arytmetyczną, dominantę, medianę

tyś zł

Najwięcej klientów zadeklarowało sumę ubezpieczenia około 35,56 tyś zł

tyś zł

Połowa klientów zadeklarowała sumę ubezpieczenia powyżej 34,82 tyś zł, a połowa poniżej.

2. Oblicz odchylenie standardowe i współczynnik zmienności

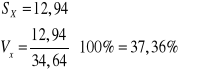
Sumy ubezpieczenia deklarowane przez klientów różnią się średnio od średniej arytmetycznej 12,94 tyś zł.

Odchylenie standardowe stanowi 37,36% średniej arytmetycznej

3. Oblicz współczynnik skośności

Szereg jest zbliżony do symetrycznego (mała skośność ujemna)

2. Przeprowadź estymację średniej arytmetycznej

• Podaj nazwę estymatora szacowanego parametru.

Estymatorem jest średnia z próby

• Podaj właściwości stosowanego estymatora i jego rozkład.

Średnia z próby jest estymatorem zgodnym, nieobciążonym, najbardziej efektywnym

Rozkładem dokładnym jest rozkład t-Studenta, ponieważ jest nieznane odchylenie standardowe populacji. Rozkładem asymptotycznym jest rozkład normalny, więc będziemy z niego korzystać.

• Czym jest estymator (liczbą, zmienną losową)?

Estymator jest zmienną losową

• Oblicz oceny parametrów na podstawie wylosowanej próby.

tyś zł S_x=12,94 tyś zł

• Oblicz błąd standardowy szacunku.

tyś zł

Średnie z prób 415 elementowych różnią się średnio od średniej w populacji o 0,635 tyś zł. Średni błąd jaki będziemy popełniać szacując średnią populacji wynosi 0,635 tyś zł.

• Przeprowadź estymację punktową szacowanego parametru.

Zakładamy, że wartość średniej w populacji jest równa średniej z próby.

tyś zł D_x=0,635 tyś zł

• Załóż wysokość współczynnika ufności.

• Odczytaj z tablic rozkładu estymatora wartość statystyki.

• Oblicz maksymalny błąd szacunku.

tyś zł

Po uwzględnieniu współczynnika ufności maksymalny błąd szacunku wynosi 1,245 tyś zł

• Przeprowadź estymację przedziałową szacowanego parametru.

Przedział ufności budujemy odejmując od oceny z próby maksymalny błąd szacunku (dolna granica) i do oceny z próby dodajemy maksymalny błąd szacunku (górna granica).

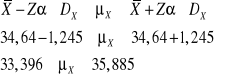
Przedział o końcach 33,396 i 35,885 tysięcy zł. ,przy współczynniku ufności

obejmie nieznaną szacowaną średnią wysokość sumy ubezpieczenia w populacji

Zakładając, że powyższa próba jest próbą pilotażową, wyznacz minimalną liczebność próby przy wsp. ufności 0,99 taką, aby maksymalny błąd szacunku był nie większy niż:

• a) 2 tyś. zł. (przedział ufności nie szerszy niż 4 tyś zł.)

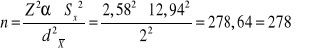
Wystarczyło wylosować 278 osób aby z maksymalnym błędem 2 tyś zł oszacować średnią populacji.

• b) 1 tyś. zł. (przedział ufności nie szerszy niż 2 tyś zł.)

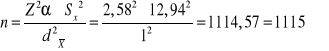
Należy wylosować 1115 osób aby z maksymalnym błędem 2 tyś zł oszacować średnią populacji.

3. Oszacuj odsetek osób, które zadeklarowały sumę ubezpieczenia powyżej 50 tyś zl.

3.1 Określ nazwę szacowanego parametru

Szacujemy wskaźnik struktury w populacji p (proporcję)

3.2 Określ nazwę estymatora i jego rozkład

Estymatorem jest częstość względna w próbie. Estymator ma rozkład asymptotycznie normalny

3.3 Oblicz ocenę parametru z próby

3.4 Oblicz błąd standardowy szacunku

1. Oblicz maksymalny błąd szacunku przy współczynniku ufności 0,95

4. Oblicz minimalna liczebność próby, taką aby maksymalny błąd szacunku był nie większy niż 2%.

5. Zakładając, że rozkład sumy ubezpieczenia jest zbliżony do normalnego, oblicz wysokość sumy ubezpieczenia powyżej której znajduje się 15% osób.

---