Programowanie komputerów

Prowadzący:

dr hab. inż. Kazimierz Worwa, prof. UW MSC

r.a. 2007/2008

UCZELNIA WARSZAWSKA

Kierunek INFORMATYKA I EKONOMETRIA

2

Programowanie komputerów

24

-

16

40

Laboratoria

Ć

wiczenia

Wykłady

RAZEM

Programowanie komputerów

3

Programowanie komputerów

LITERATURA

Schildt H.:Programowanie: Wydawnictwo RM, Warszawa, 2002.

Aho A.V., Ullman J.D.: Wykłady z informatyki z przykładami w j

ę

zyku

C. Wydawnictwo HELION, Gliwice, 2003.

Loudon K.: Algorytmy w C. Wydawnictwo HELION, Gliwice, 2003.

Reek K.A.: J

ę

zyk C. Wska

ź

niki. Wydawnictwo HELION, Gliwice, 2003.

4

Programowanie komputerów

Lokalizacja plików do wykładów

http://members.lycos.co.uk/pkjw84/kw/

logowanie:

nazwa u

ż

ytkownika

2007/2008

hasło

kw

5

Programowanie komputerów

Tematyka przedmiotu

Architektura komputera

Systemy zapisu liczb

Poj

ę

cie algorytmu – rodzaje, sposoby zapisu

Struktura programu w j

ę

zyku C

Procedury i funkcje

Instrukcje steruj

ą

ce

Typy danych, zmienne i wyra

ż

enia

Statyczne struktury danych

Dynamiczne struktury danych

Operacje wej

ś

cia/wyj

ś

cia

Typy zło

ż

one: struktury i unie

Przykłady typowych algorytmów w j

ę

zyku C

(algorytmy wyszukiwania, sortowania itp.)

Zło

ż

ono

ść

obliczeniowa algorytmów

Programowanie komputerów

Wykład 1

Architektura komputera

Systemy zapisu liczb

Poj

ę

cie algorytmu – rodzaje, sposoby zapisu

7

Programowanie komputerów

Elementy architektury komputerów

Architektura komputera – okre

ś

la charakterystyczne cechy

komputera, wskazuj

ą

c sposób poł

ą

czenia i współpracy

elementów składowych.

Architektura komputera okre

ś

la jego elementy z punktu

widzenia jego u

ż

ytkownika (programisty)

8

Programowanie komputerów

Procesor

Pamięć ROM

Pamięć RAM

(oprogramowanie operacyjne)

(programy użytkowe)

Układy wejścia

Układy wyjścia

- klawiatura
- mysz
- skaner
- pamięć dyskowa

- drukarka
- pamięć dyskowa

- monitor ekranowy

- ploter

- czytniki

dokumentów

(magnetyczne MICR,

optyczne OCR)

Elementy architektury komputerów

9

Programowanie komputerów

Procesor (jednostka centralna komputera) – urz

ą

dzenie do

przetwarzania informacji w sposób okre

ś

lony przez

u

ż

ytkownika. Procesor słu

ż

y do wykonywania (szybkiego)

elementarnych operacji

Mikroprocesor - procesor wykonany w postaci jednego
mikroukładu o wielkim stopniu scalenia

Mikrokomputer (system mikroprocesorowy) – zespół
elementów umo

ż

liwiaj

ą

cych samodzieln

ą

realizacj

ę

zada

ń

obliczeniowych. Składa si

ę

z mikroprocesora oraz urz

ą

dze

ń

dodatkowych (w tym urz

ą

dze

ń

we/wy)

Elementy architektury komputerów

10

Programowanie komputerów

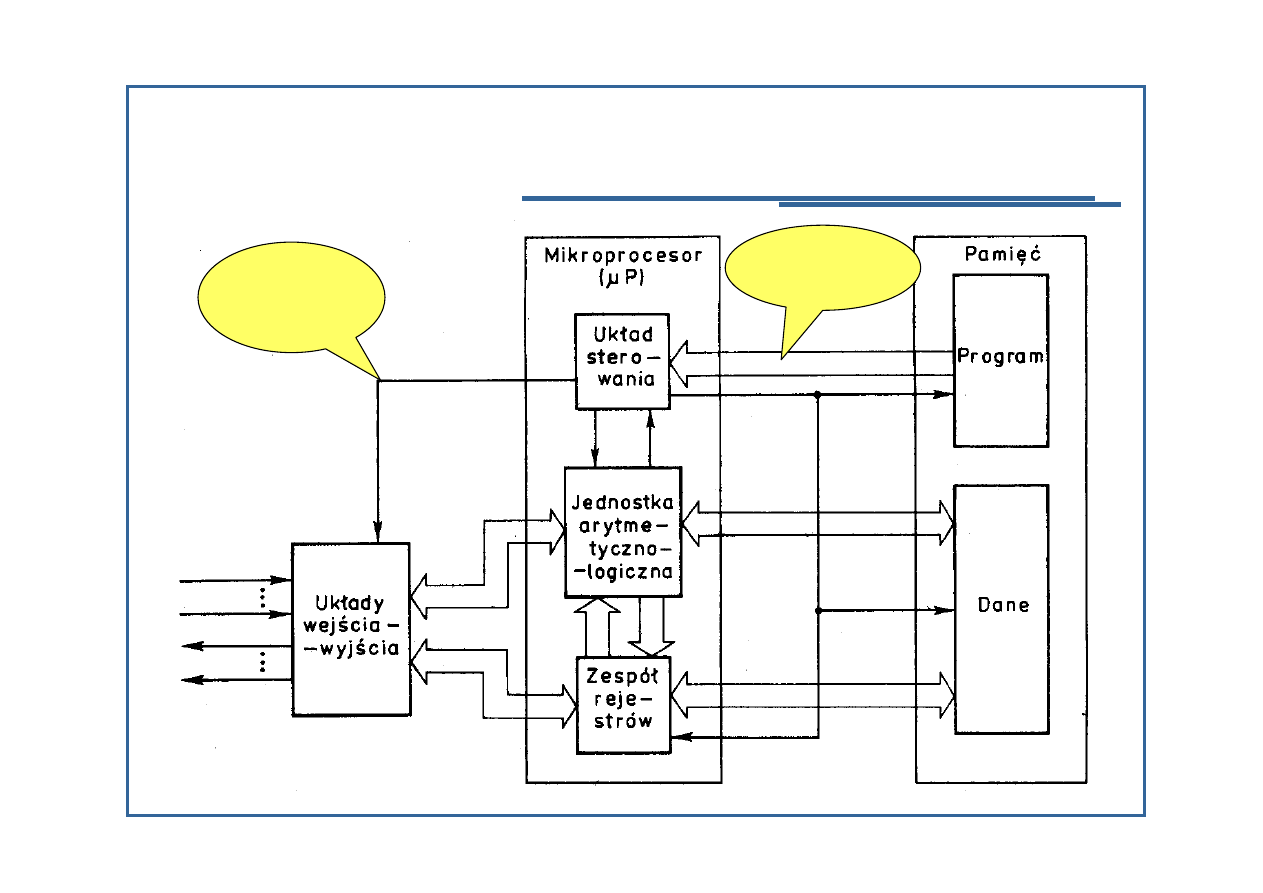
W skład architektury mikroprocesora wchodz

ą

:

układ steruj

ą

cy, do kierowania przebiegiem oblicze

ń

(z

dekoderem rozkazów) .

zespół rejestrów, do przechowywania warto

ś

ci danych i

wyników;

jednostka arytmetyczno-logiczna (JAL), do wykonywania
podstawowych (prostych) operacji na danych

Rejestry

procesora

JAL

Układ

sterujący

Sygnały

sterujące

Argumenty,

wyniki

Elementy architektury komputerów

11

Programowanie komputerów

Układ steruj

ą

cy

Ma za zadanie sterowanie prac

ą

wszystkich pozostałych bloków

mikroprocesora (rejestry, JAL) i mikrokomputera (pami

ęć

,

urz

ą

dzenia WE/WY).

Układ ten pobiera kolejne rozkazy do wykonania oraz dane
potrzebne do wykonania tej operacji.

Po wykonaniu operacji przekazuje uzyskane wyniki w
odpowiednie miejsce.

W skład układu sterowania wchodzi tzw. dekoder rozkazów i
rejestr rozkazów.

Elementy architektury komputerów

12

Programowanie komputerów

Rejestry mikroprocesora s

ą

wykorzystywane przez jednostk

ę

arytmetyczno-logiczn

ą

zazwyczaj jako

ź

ródło danych dla

wykonywanych operacji lub jako miejsce umieszczenia wyników

Jednostka arytmetyczno-logiczna wykonuje operacje zlecone
przez układ sterowania i

ś

ci

ś

le współdziała z rejestrami procesora.

Typowe operacje:

działania arytmetyczne (dodawania, odejmowanie,
porównywanie dwóch liczb, zmiana znaku)

działania logiczne (suma logiczna (OR), iloczyn logiczny (AND),
suma modulo 2 (XOR), negacja)

przesuni

ę

cia (w lewo, w prawo),

działania na pojedynczych bitach (ustawianie bitu, zerowanie
bitu, testowanie bitu)

Elementy architektury komputerów

13

Programowanie komputerów

Przesyłanie

danych

Sygnały

sterujące

Elementy architektury komputerów

14

Programowanie komputerów

System dwójkowy

System dwójkowy jest

naturalnym systemem informatyki

Jak zapisujemy informacj

ę

?

Za pomoc

ą

zjawisk elektrycznych, magnetycznych, optycznych

Zamiast skomplikowanych pomiarów które by pozwoliły zapisa

ć

10 cyfr

mamy proste i jednoznaczne kodowanie.
•

Materiał półprzewodnikowy: gdy przyło

ż

ymy napi

ę

cie w jednym

kierunku przewodzi pr

ą

d (prawie idealnie), a w kierunku przeciwnym

nie przewodzi pr

ą

du. Mamy wiec dwa stany

•

Podobnie jest w magnetyzmie: substancje magnetyczne mo

ż

na

namagnesowa

ć

w dwóch kierunkach

Wad

ą

systemu dwójkowego jest długo

ść

liczby, np.

(0010001110100101)

2

= 2

13

+ 2

9

+ 2

8

+ 2

7

+ 2

5

+ 2

2

+ 2

0

= (9125)

10

15

Programowanie komputerów

Elementarn

ą

jednostk

ą

informacji jest bit

•

Bit jest to

podstawowa elementarna jednostka informacji

wystarczaj

ą

ca do zakomunikowania jednego z co najwy

ż

ej dwóch

jednakowo prawdopodobnych zdarze

ń

.

•

Bit stanowi podstaw

ę

zapisu informacji w ró

ż

nych typach pami

ę

ci

komputera.
Wszystkie inne jednostki stanowi

ą

ró

ż

n

ą

wielokrotno

ść

bitów.

•

Symbolicznie warto

ść

bitu oznacza si

ę

jako „0” lub „1”

Jest to oznaczenie stosowane w matematyce oraz przy opisie
informacji przechowywanej w pami

ę

ci komputera i opisie sposobów

kodowania informacji

.

Jednostki informacji

16

Programowanie komputerów

Bajty

•

Przyj

ę

ło si

ę

stosowanie

jednostki licz

ą

cej 8 bitów

, zwanej

bajtem

•

Bajt to

podstawowa komputerowa jednostka informacji

•

W praktyce stosujemy

kilobajty

,

megabajty

,

gigabajty

,

terabajty

,...

Jeden bajt mo

ż

e reprezentowa

ć

256 ró

ż

nych warto

ś

ci,

które mog

ą

oznacza

ć

zapisywane informacje

10

3

(tysi

ą

c)

2

10

= 1 024

Kilobajt (kB)

10

12

(bilion)

2

40

= 11 099 511 627 776

Terabajt (TB)

10

9

(miliard)

2

30

= 1 073 741 824

Gigabajt (GB)

10

6

(milion)

2

20

= 1 048 576

Megabajt (MB)

Potoczne rozumienie

Liczba bajtów

Nazwa

17

Programowanie komputerów

Elementy arytmetyki komputerów

2

0

=1

2

1

=2

2

2

=4

2

3

=8

2

4

=16

2

5

=32

2

6

=64

2

7

=128

2

8

=256

2

9

=512

2

10

B=1kB=1024B

2

20

B=MB=1024kB=1024*1024B

2

30

B=1GB=1024MB=1024*1024*1024B

2

40

B=1TB=1024GB=1024*1024*1024KB=...

bajt (B)= 8 bitów

18

Programowanie komputerów

Systemy zapisu liczb

Na ogół operujemy systemami pozycyjnymi, np. rzymski, dziesi

ę

tny.

System pozycyjny

tzn.

ż

e warto

ść

danej cyfry zale

ż

y od jej

miejsca ( poło

ż

enia) w ci

ą

gu cyfr

„rzymski” = system pozycyjny sekwencyjny

„dziesi

ę

tny” = system pozycyjny wagowy

(x

k-1

, x

k-2

,…,x

1

,x

0

x

–1

, x

–2

, x

–m

)

gdzie:

n, m ≥ 0, N

≥

2, a

i

∈

{0,....,B-1}

B

nazywamy podstaw

ą

systemu, za

ś

a

i

jest elementem zbioru cyfr

dost

ę

pnych w danym systemie

W systemie dziesi

ę

tnym:

B = 10, a

i

∈

∈

∈

∈

{ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 }

L =

∑

a

i

B

i

i=-m

n

19

Programowanie komputerów

Reprezentacja wartości liczbowych

Arytmetyka stałoprzecinkowa (przykłady realizacji)

Naturalny kod dwójkowy

Kod znak – moduł

System uzupełnieniowy do 2

Arytmetyka zmiennoprzecinkowa

zapis cecha-mantysa

20

Programowanie komputerów

Naturalny kod dwójkowy

Liczba X, k+m cyfrowa, z k cyframi przez przecinkiem i m
cyframi po przecinku, reprezentowana jest przez ci

ą

g cyfr

(x

k-1

, x

k-2

,…,x

1

,x

0

x

–1

, x

–2

, x

–m

)

Jej warto

ść

mo

ż

na przedstawi

ć

za pomoc

ą

wzoru:

gdzie B jest podstaw

ą

systemu.

Dla B=2, X nale

żą

cego do zbioru liczb ca

ł

kowitych oraz

wzór przyjmuje posta

ć

:

∑

−

−

=

=

1

k

m

i

i

i

B

x

X

}

{

1

,...,

1

,

0

x

i

−

∈

Β

}

{

1

,

0

x

i

∈

∑

−

−

=

=

1

2

k

m

i

i

i

x

X

21

Programowanie komputerów

Naturalny kod dwójkowy

Przykłady:

100101

2

= 37

10

101010

2

= 42

10

10.1

2

= 2,5

10

101.101

2

= 5,625

10

110.011

2

= 6,375

10

22

Programowanie komputerów

Naturalny kod dwójkowy

Konwersja do systemu binarnego

Przy wyznaczaniu reprezentacji całkowitej, kolejnymi
(pocz

ą

wszy od najmniej znacz

ą

cej) cyframi w reprezentacji

dwójkowej s

ą

reszty z dzielenia liczby przez dwa.

Przy wyznaczaniu cz

ęś

ci u

ł

amkowej kolejnymi cyframi b

ę

d

ą

cz

ęś

ci ca

ł

kowite podwajanych pozosta

ł

o

ś

ci u

ł

amkowych

(pocz

ą

wszy od najbardziej znacz

ą

cej).

Przykład konwersji:

11

10

X

2

Liczba

:

Wynik Reszta

11

:2

5

1

5

:2

2

1

2

:2

1

0

1

:2

0

1

Wynik konwersji: 1011

2

23

Programowanie komputerów

Naturalny kod dwójkowy

Przykład konwersji: 0.125

10

X

2

Liczba

x

Wynik Część

całkowita

0.125

*2

0.25

0

0.25

*2

0.5

0

0.5

*2

1

1

Wynik konwersji: 0.125

10

X

2

:0.001

2

Wadą naturalnego systemu binarnego jest to, że nie można
przy jego pomocy przedstawić liczb ujemnych

24

Programowanie komputerów

Kod znak – moduł

Jedn

ą

z metod reprezentacji liczb ujemnych jest reprezentacja

znak-moduł,

w

której

znak

liczby

jest

kodowany

dwuwarto

ś

ciowo na najbardziej znacz

ą

cej pozycji.

Warto

ść

liczby zakodowanej w tym systemie mo

ż

na policzy

ć

ze wzoru:

∑

−

−

=

−

=

2

2

)

1

(

k

m

i

i

i

s

x

X

gdzie

jest kodem znaku liczby

}

{

1

,

0

s

∈

x

k-1

x

k-2

x

k-3

x

−

m

s

...

...

...

...

...

...

...

25

Programowanie komputerów

Kod znak – moduł

Przykłady:

011011

2

= 27

10

111011

2

=

−

27

10

0101.11

2

= 5,75

10

1101.11

2

=

−

5,75

10

26

Programowanie komputerów

Kod znak – moduł

Wadami tego systemu s

ą

:

podwójna reprezentacja zera (+0, -0):

0000

2

= 0

10

1000

2

= -0

10

konieczno

ść

osobnego przetwarzania znaków argumentowych

przy wykonywaniu operacji arytmetycznych, a zw

ł

aszcza

sposobu wykonywania operacji dodawania i odejmowania
w zale

ż

no

ś

ci od znaków operandów.

27

Programowanie komputerów

System uzupełnieniowy do 2 (U2)

Powszechnym sposobem reprezentacji stałoprzecinkowych
liczb znakowych (liczb ca

ł

kowitych) jest dwójkowy system

uzupełnieniowy do dwóch.

Warto

ść

liczby (x

k-1

,…,x

1

, x

0

...x

-m

) dana jest wzorem:

∑

−

−

=

−

−

+

−

=

2

1

1

2

2

k

m

i

i

i

k

k

x

x

X

x

k-1

x

k-2

x

k-3

x

−

m

s

...

...

...

...

...

...

...

kropka dziesiętna

28

Programowanie komputerów

System uzupełnieniowy do 2

Przyk

ł

ad konwersji U2

10:

1011

U2

= –1*2

3

+ 0*2

2

+ 1*2

1

+ 1*2

0

= – 8 + 3 = – 5

10

Najbardziej znacz

ą

c

ą

pozycj

ę

liczby k-bitowej mo

ż

emy

traktowa

ć

jako kod jej znaku.

29

Programowanie komputerów

System uzupełnieniowy do 2

Dalsze przykłady U2

10:

1010

U2

= –1*2

3

+ 0*2

2

+ 1*2

1

+ 0*2

0

= – 8 + 2 = – 6

10

1101.101

U2

= –1*2

3

+ 1*2

2

+ 0*2

1

+ 1*2

0

+ 1*2

-1

+ 0*2

-2

= 1*2

-3

=

= – 8 + 4 + 1 + 0,5 + 0,125 = – 3,625

10

30

Programowanie komputerów

System uzupełnieniowy do 2

Ciąg bitów

Reprezentowana wartość

0111

7

0110

6

0101

5

0100

4

0011

3

0010

2

0001

1

0000

0

1111

−

1

1110

−

2

1101

−

3

1100

−

4

1011

−

5

1010

−

6

1001

−

7

1000

−

8

31

Programowanie komputerów

Potoczne rozumienie pojęcia „algorytm”

Potocznie algorytm jest rozumiany jako pewien przepis na
wykonanie zestawu czynno

ś

ci, prowadz

ą

cych do osi

ą

gni

ę

cia

oczekiwanego i z góry okre

ś

lonego celu

Dzisiejsze, uogólnione znaczenie słowa algorytm:

zbiór reguł post

ę

powania, umo

ż

liwiaj

ą

cych rozwi

ą

zanie

okre

ś

lonego zadania w sko

ń

czonej liczbie kroków i w sko

ń

czonym

czasie

Dziedzina wiedzy zajmuj

ą

c

ą

si

ę

badaniem algorytmów nazywa si

ę

algorytmik

ą

32

Programowanie komputerów

Pojęciowy model algorytmu

Algorytm mo

ż

e by

ć

rozumiany jako pewne odwzorowanie

f

,

które dla okre

ś

lonego zestawu danych wej

ś

ciowych

We

generuje okre

ś

lony zestaw danych wyj

ś

ciowych

Wy

:

f: We

Wy

Dane

wejściowe

We

Dane

wyjściowe

Wy

f

33

Programowanie komputerów

S

posoby zapisu algorytmów

Algorytm powinien precyzyjnie opisywa

ć

kolejne jego kroki.

Do przedstawienia algorytmu stosuje si

ę

:

opis werbalny,

zapis formalny, np.:

zapisy graficzne (schematy blokowe),

formalne specyfikacje programów (np.VDM)

zapisy w postaci pseudokodu (paraprogramu)

zapis algorytmu w dowolnym j

ę

zyku programowania

34

Programowanie komputerów

Język programowania

J

ę

zyk programowania jest

ś

rodkiem umo

ż

liwiaj

ą

cym zapis

algorytmów w postaci zrozumiałej dla człowieka, a równocze

ś

nie

przetwarzalnej do postaci zrozumiałej dla komputera.

Kod źródłowy programu
(w języku programowania)

Kod wynikowy programu
(w języku maszynowym)

Przetworzenie

programu

źródłowego

w kod

maszynowy

35

Programowanie komputerów

Klasyfikacja algorytmów

Rozwa

ż

a

ć

b

ę

dziemy nast

ę

puj

ą

ce klasy algorytmów:

algorytmy sekwencyjne - algorytmy równoległe;

algorytmy numeryczne - algorytmy nienumeryczne;

algorytmy rekurencyjne - algorytmy iteracyjne.

36

Programowanie komputerów

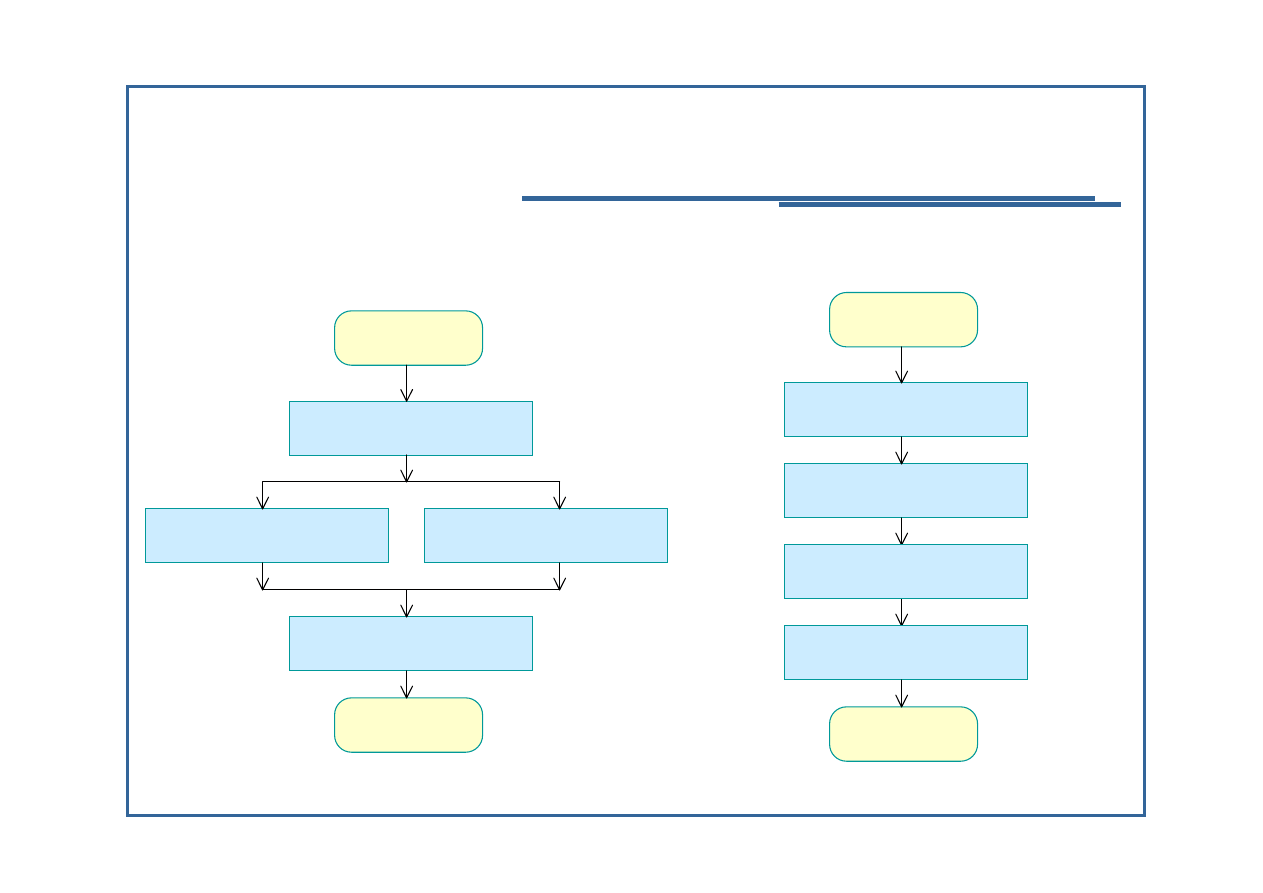
Przykład - pierwiastki równania kwadratowego

START

STOP

∆∆∆∆

=b

2

-4ac

x

1

=(-b-sqrt(

∆∆∆∆

))/2a

x

2

=(-b+sqrt(

∆∆∆∆

))/2a

Wypisz x

1

, x

2

START

STOP

∆∆∆∆

=b

2

-4ac

x

1

=(-b-sqrt(

∆∆∆∆

))/2a

x

2

=(-b+sqrt(

∆∆∆∆

))/2a

Wypisz x

1

, x

2

Algorytm równoległy: Algorytm sekwencyjny:

0

c

bx

ax

2

=

+

+

37

Programowanie komputerów

Wywołanie funkcji rekurencyjnej

Rekurencja oznacza wywołanie funkcji (procedury) przez t

ę

sam

ą

funkcj

ę

(procedur

ę

)

Niepo

żą

dana cecha definicji rekurencyjnych: aby wyznaczy

ć

n-t

ą

warto

ść

trzeba najpierw wyznaczy

ć

wszystkie

„wcze

ś

niejsze” warto

ś

ci

Wa

ż

ne jest, aby kolejne wywołania funkcji (procedury)

rekurencyjnej były realizowane dla kolejnych warto

ś

ci

parametrów formalnych w taki sposób, aby nie doszło do
zjawiska „niesko

ń

czonej p

ę

tli rekurencyjnych wywoła

ń

funkcji”

38

Programowanie komputerów

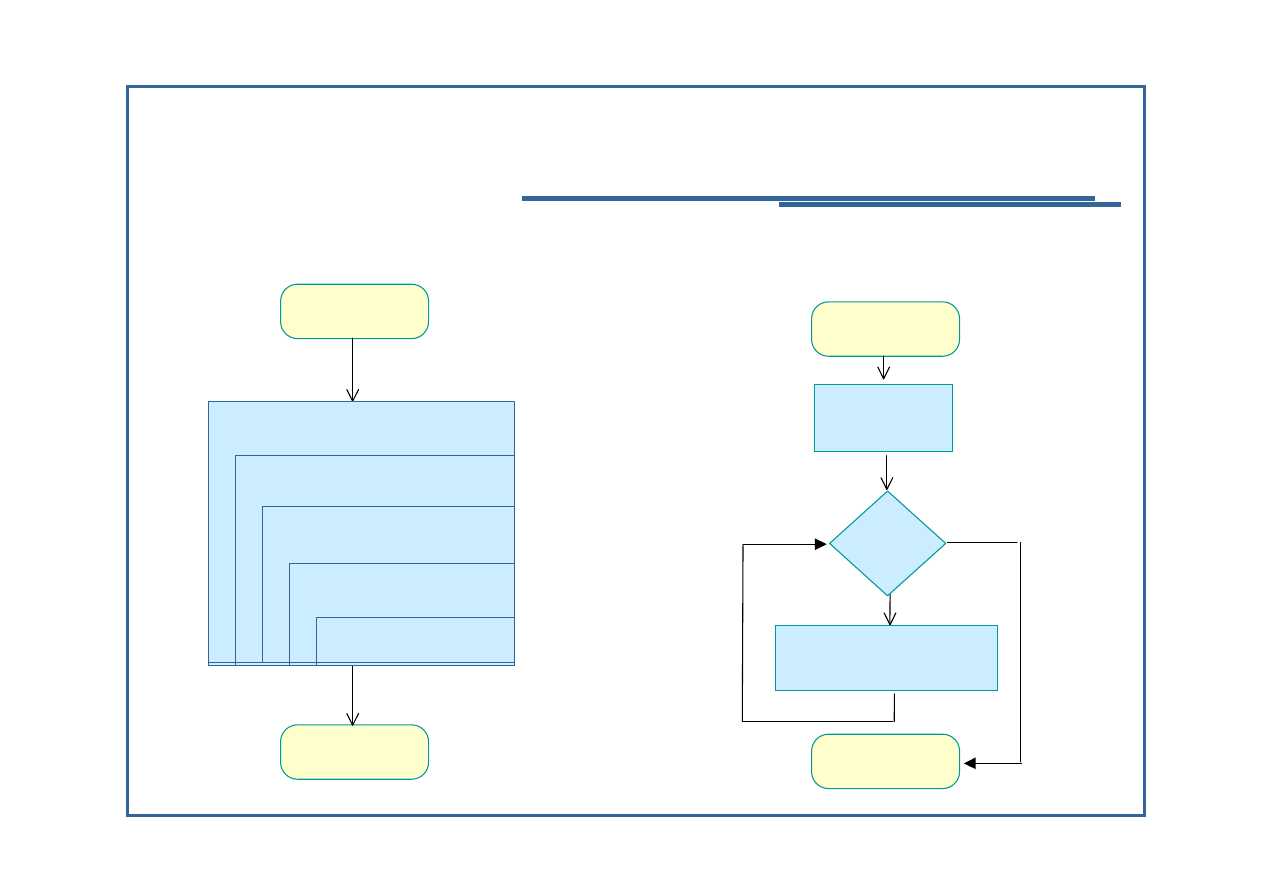
Przykład obliczania n! dla n=5

Algorytm rekurencyjny: Algorytm iteracyjny

START

STOP

= 5 * 4!

= 4 * 3!

3 * 2!

2 * 1!

1

= 4 * 3!

= 3 * 2!

= 2 * 1!

= 1

START

STOP

Silnia = 1

i=1

i

≤≤≤≤

5

Silnia = Silnia*i

i=i+1

T

N

39

Programowanie komputerów

Przykłady funkcji rekurencyjnych

Funkcja „silnia”:

1

dla n=0

(warunek zako

ń

czenia rekurencji)

n!=

n*(n-1)!

dla n>0

Definicja pewnego ci

ą

gu liczb wymiernych:

1

dla n=0

(warunek zako

ń

czenia rekurencji)

f(n)=

f(n-1) + 1/f(n-1), dla n>0,

okre

ś

la ci

ą

g o warto

ś

ciach:

1, 2, 5/2, 29/10, 941/290, 969581/272890,.................

40

Programowanie komputerów

Funkcja rekurencyjna – ciąg Fibonacciego

Ci

ą

g Fibonacciego :

n

dla n<2

Fib(n)=

Fib(n-2) + Fib(n-1) dla n>=2

Rekurencyjna implementacja w j

ę

zyku C:

long int Fib (int n)

{

if (n<2)

return n;

else

return Fib(n-2) + Fib (n-1);

}

Czy na pewno stos programu

„wytrzyma” taką realizację

funkcji

rekurencyjnej Fib?

41

Programowanie komputerów

Jak procesor „widzi” program?

Pisz

ą

c program w j

ę

zyku programowania widzimy jego

polecenia, instrukcje steruj

ą

ce, zmienne, stałe itp.

Procesor potrafi jedynie wykonywa

ć

polecenia ze swojej listy

rozkazów(w postaci) j

ę

zyka maszynowego, czyli tzw.

assemblera.

Za przeniesienie programu z postaci

ź

ródłowej w j

ę

zyku

programowania do j

ę

zyka maszynowego procesora jest

odpowiedzialny „kompilator j

ę

zyka programowania”

Kod źródłowy programu
(w języku programowania)

Kod wynikowy programu
(w języku maszynowym)

Przetworzenie

programu

źródłowego

w kod

maszynowy

42

Programowanie komputerów