Automatyka i Robotyka –Analiza – Wykład 23 – dr Adam Ćmiel – cmiel@agh.edu.pl
1
SZEREGI POTĘGOWE
−
)
(
n
c
ciąg liczb zespolonych
∑
∞
=
−
0
0
)
(
n
n
n
z
z
c
- szereg potęgowy,
gdzie (
n
c
)- ciąg współczynników szeregu,
0
z
∈C - środek, „centrum” (ustalone),
z
∈C - zmienna.
Dla dowolnego ustalonego
z
∈C szereg potęgowy może być zbieżny albo rozbieżny. Jeżeli szereg
∑
∞
=
−
0
0
)
(
n
n
n
z
z
c
jest zbieżny w pewnym punkcie w∈C , to jest on zbieżny w każdym kole domkniętym
r
z
z
≤
−
|
|
0
, gdzie r<|w-z
0
|. Rzeczywiście ze zbieżności szeregu
∑
∞
=
−
0
0
)
(
n
n
n
z
w
c
i z WK zbieżności
szeregu mamy
0
)
(
lim
0
=
−
∞
→
n
n
n
z
w
c
, a stąd
K
z
w
c
n
n
≤
−
|
)
(
|
0
. Wobec tego dla
z
∈C spełniających
warunek 0<
r
z
z
≤
−
|
|
0
, gdzie r<|w-z
0
| dostajemy
n
n
n
n
n
n
Kq
z
w
z
z
z
w
c
z
z
c
≤
−
−
−
≤
−
|
|
|
|
|
)
(
|
|
)
(
|
0
0
0
0
, gdzie 0<q<1. Stąd teza
Podobnie jeśli szereg jest rozbieżny w pewnym punkcie w , to jest rozbieżny dla
z
∈C spełniających
warunek
r
z
z
≥
−
|
|
0
, gdzie r<|w-z
0
|.
Wobec tego, z każdym szeregiem potęgowym związane jest tzw. koło zbieżności. Jeżeli
z
∈C leży
we wnętrzu koła zbieżności, to szereg jest zbieżny. Jeżeli na zewnątrz – to rozbieżny, zaś jeżeli z leży
na okręgu koła, to badanie zbieżności wymaga stosowania specjalnych metod.
Tw: (
O promieniu zbieżności R szeregu potęgowego
)
Jeżeli istnieje granica
n
n
n
c
c
1
sup
lim
+
∞
→
=
α
(d’Alambert)
lub
n
n
n
c
sup
lim
∞
→
=
α
(Cauchy)
,
to
∞
=
=
∞
∞
<
<
=
α
α
α
α
0
0
0
1
R
Dow. (fragment)
z
∈C – dowolnie ustalone, badamy bezwzględną zbieżność
∑
∞
=
−
0
0
)
(
n
n
n
z
z
c
.
Dla ustalonego
z
∈C szereg liczbowy
∑
∞
=
−
0
0
)
(
n
n
n
z
z
c
jest szeregiem o wyrazach nieujemnych.
Z kryterium d’Alamberta
0
0
1
0
1
0
1
sup
lim
sup
lim
z
z
z
z
c
c
z
z
c
z
z
c
g
n
n
n
n
n
n
n
n
−
=
−
=
−
−
=
+
∞
→
+
+
∞
→
α
,
więc gdy
1
0
<
− z
z
α
szereg jest zbieżny. Wobec tego dla
z
∈C spełniających warunek
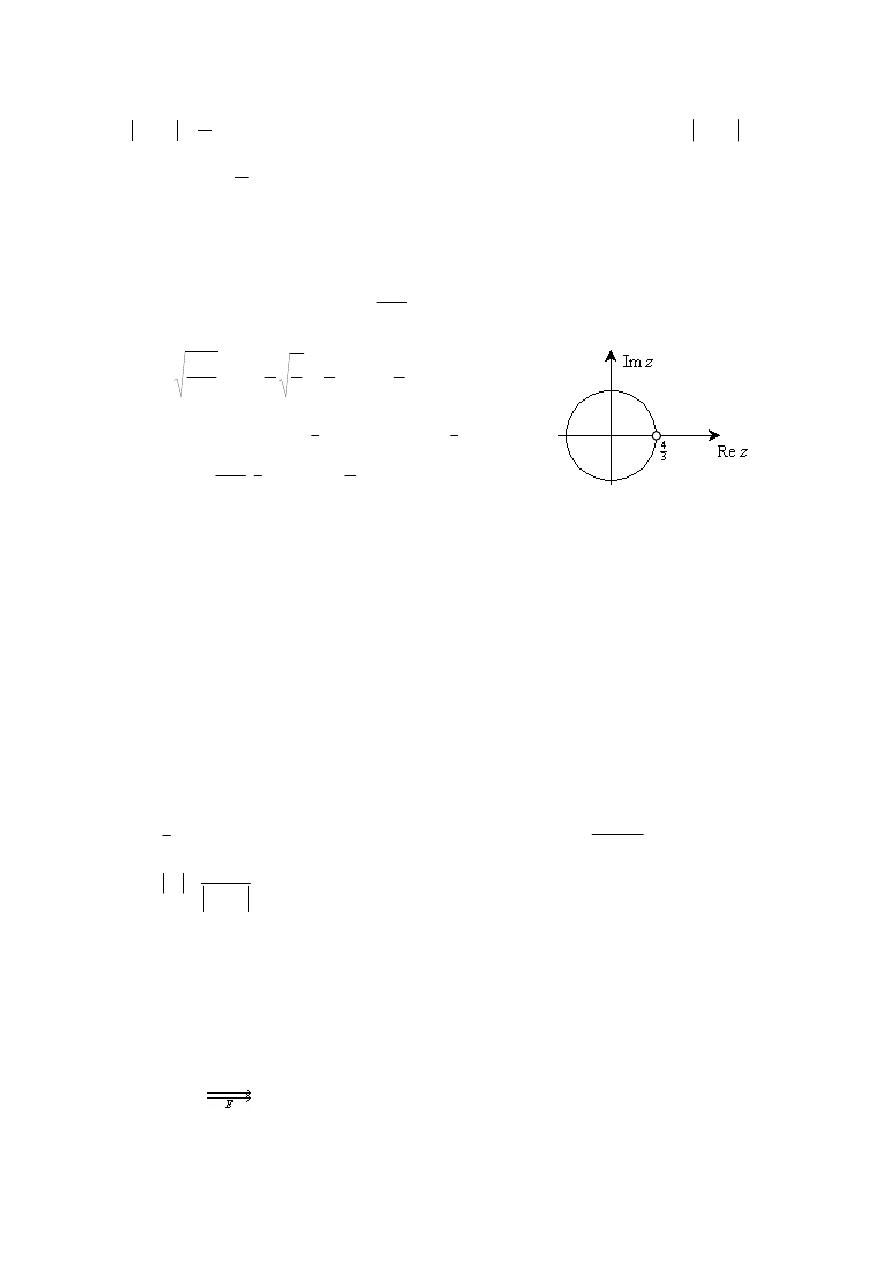
Automatyka i Robotyka –Analiza – Wykład 23 – dr Adam Ćmiel – cmiel@agh.edu.pl
2
α
1
0
<
− z
z
(
∞
≠
∧
≠
α
α
0
) – szereg jest zbieżny czyli jest także zbieżny w kole
R
z
z
<
−
0
o
promieniu
α
1
=
R
. (Podobnie dla
∞
=
∨
=
α
α
0
).
Z kryterium Weierstrassa wynika ponadto, że szereg potęgowy jest jednostajnie zbieżny, w
każdym kole domkniętym zawartym w kole zbieżności (bez brzegu!)
Przykład. Zbadać obszar zbieżności
∑
∞
=
+
1
1
4
3
n
n
n
n
z
n
3
4
4
3
3
4
3
lim
4
3
lim
1
=
⇒
=
=
=
∞
→
+
∞
→
R
n
n
n
n
n
n
n
n
α
jeżeli z leży na okręgu ⇔ z=
ϕ
ϕ
ϕ
i
e
i
3
4
3
4
)
sin
(cos
=
+
i wówczas
( )
∑
∑
∞
=
∞
=
+
=
1
1
3
4
1
3
4
3
n
in
n
in
n
n
n
e
n
e
n
ϕ
ϕ
Tw.
Kryterium Dirichleta. Jeżeli
• ciąg (a
n
) jest ciągiem monotonicznie malejącym do zera
•
M
z
f
z
S
n
k
k
n
E
z
n
≤
=
∀
∀
∑
=
∈
|
)
(
|
|
)
(
|
0
(czyli ciąg sum częściowych
∑
=
n
k
k
z
f
0
)
(
jest ograniczony)
to szereg
∑
∞
=0
)
(
n
n
n
z
f
a
jest jednostajnie zbieżny w zbiorze E
Jeżeli w powyższym kryterium ustalimy
z
∈C, to otrzymamy jeszcze jedno kryterium zbieżności
szeregu liczbowego (
∑
∞
=0
n
n
n
b
a
, gdzie
)
(z
f
b
n
n
=
).
Ciąg dalszy przykładu
0
≠
ϕ
0
3
↓
n
( )
...
1
1
=
=
=
∑
∑
=
=
n
k
k
i
n
k
k
i
n
e
e
S
ϕ
ϕ
ciąg geometryczny
ϕ
ϕ
ϕ
i
in
i
e
e
e
−
−
=
1
1
...
0
1
2
≠
∀
⇒
−
≤
ϕ
ϕ
i
n
e
S
, stąd dla
0
≠
ϕ
szereg jest zbieżny.
Dla
0
=
ϕ
dostajemy szereg harmoniczny (rozbieżny)
W przypadku rzeczywistym kołem zbieżności jest przedział na osi, a jego brzegiem końce przedziału.
Zbieżność jednostajna a ciągłość
Tw. Jeżeli
•
R
E
f
n
→
:
jest ciągiem funkcji ciągłych na E
•
n
f
f
to
f
jest ciągła na E
Automatyka i Robotyka –Analiza – Wykład 23 – dr Adam Ćmiel – cmiel@agh.edu.pl
3
Wnioski:
)
(
)
(
lim
)
(
lim
lim
0
0
0
x
f
x
f
x
f
x
x
n
n
x
x
=
=
→
∞
→
→
=
)
(
lim
lim
)
(
lim
0
0
x
f
x
f
n
x
x
n
n
n
→
∞
→
∞
→
=
(zmiana kolejności granic)
Tw.
(wariant dla szeregu) Jeżeli
•
R
E
f
n
→
:
jest ciągiem funkcji ciągłych na E
• Szereg
∑
∞
=
−
1
)
(
n
n
x
f
zbieżny jednostajnie na E
to
∑
∞
=1
)
(
szeregu
suma
n
n
x
f
jest funkcją ciągłą na E
Wniosek:
∑
∑
∑
∞
=
∞
=
→
∞
=
→
=
=
1
0
1
1
)
(
)
(
lim
)
(
lim
0
0
n
n
n
n
x
x
n
n
x
x
x
f
x
f
x
f
Jeżeli szereg funkcji ciągłych jest jednostajnie zbieżny, to można przejść do granicy wyraz po
wyrazie.
Zbieżność jednostajna a całkowanie
Tw:
(zbieżność jednostajna a całkowanie) Jeżeli
•
]
,
[ b
a
f
n
n
R
∈
∀
(całkowalna w sensie Riemanna)
•
n
f
f
, gdzie
]
,
[ b
a
E
=
to
]
,
[ b
a
f
R
∈
i
∫
∫
∞
→
=
b
a
n
n
b
a
dx
x
f
dx
x
f
)
(
lim
)
(
Tw.
(wariant dla szeregu)
•
]
,
[ b
a
f
n
n
R
∈
∀
• Szereg
∑
∞
=
−
1
)
(
n
n
x
f
jednostajnie zbieżny
to
]
,
[
)
(
1
b
a
x
f
n
n
R
∈
∑
∞
=
i
∑∫
∫ ∑
∞
=
∞
=
=
1
1
)
(
)
(
n
b
a
n
b
a
n
n
dx
x
f
dx
x
f
Szereg jednostajnie zbieżny funkcji całkowalnych w sensie Riemanna można całkować wyraz po
wyrazie.
Zbieżność jednostajna a różniczkowalność
Uwaga: Ciąg
)
sin(
)
(
1
nx
x
f
n
n
=
funkcji różniczkowalnych na R jest jednostajnie zbieżny do
0
)
(
≡
x
f
, a ciąg pochodnych
)
cos(
)
(
'
nx
x
f
n
=
nie jest nawet punktowo zbieżny (np. rozbieżny dla
2
π
=
x
)
Tw. Jeżeli
•
R
b
a
f
n
n
→
∀
]
,
[
:
różniczkowalna na
]
,
[
b
a
• ciąg liczbowy
)
(
0
x
f
n
jest zbieżny dla pewnego
]
,
[
0
b
a
x
∈
•
n
f ′
jest jednostajnie zbieżny na
]
,
[
b
a

Automatyka i Robotyka –Analiza – Wykład 23 – dr Adam Ćmiel – cmiel@agh.edu.pl
4
to ciąg funkcyjny
n
f
jest jednostajnie zbieżny na
]
,
[
b
a
do pewnej różniczkowalnej funkcji f
(
n
f
f
) i
)
(
'
)
(
lim
]
,
[
x
f
x
f
n
n
b
a
x
=
′
∀
∞
→
∈
Tw:
(wariant dla szeregu) Jeżeli
•
n
n
f
∀
różniczkowalne na
]
,
[
b
a
• Szereg
∑
∞
=
−
1
0
)
(
n
n
x
f
zbieżny dla pewnego
]
,
[
0
b
a
x
∈
•
∑
∞
=
′
1
)
(
n
n
x
f
jednostajnie zbieżny na
]
,
[
b
a
to szereg
∑
∞
=1
)
(
n
n
x
f
jest jednostajnie zbieżny na
]
,
[
b
a
i
∑
∑
∞
=
∞
=
′
=
′
1
1
)
(
)
(
n
n
n
n
x
f
x
f
Zastosowanie do szeregów potęgowych
.
Def. Jeżeli f ma przedstawienie w postaci
∑
∞
=
−
=
0
0
)
(
)
(
n
n
n
z
z
c
z
f
,
C
z
z
c
n
∈
0
,
,
, to f nazywamy
funkcją analityczną.
Ponieważ nie wprowadzono pojęcia pochodnej funkcji
C
C
f
→
:
, ani całki takiej funkcji,
ograniczmy się do funkcji zmiennej rzeczywistej.
∑
∞
=
−
=
0
0
)
(
)
(
n
n
n
x
x
c
x
f
,
R
x
x
c
n
∈
0
,
,
Załóżmy, że szereg
∑
∞
=
−
0
0
)
(
n
n
n
x
x
c
jest zbieżny w przedziale
R
x
x
<
−
|
|
0
. Wówczas
• szereg ten jest jednostajnie zbieżny w każdym przedziale postaci
]
,
[
0
0
ε
ε
−
+
+
−
R
x
R
x
.
• suma szeregu
∑
∞
=
−
=
0
0
)
(
)
(
n
n
n
x
x
c
x
f
jest ciągła i różniczkowalna na
)
,
(
0
0
R
x
R
x
+
−
, oraz
∑
∑
∞
=
−
∞
=
−
=
′
=
′
0
1
0
0
)
(
)
(
n
n
n
n
n
x
x
nc
f
x
f
(szereg po zróżniczkowaniu ma taki sam promień
zbieżności jak szereg wyjściowy)
∑
∞
=
−
−
+
−
⋅
⋅
−
=
0
0
)
(
)
(
)
1
(
...
)
1
(
)
(
n
k
n
n
k
x
x
c
k
n
n
n
x
f
=
∑
∞
=
−
−
+
−
⋅
⋅
−
k
n
k
n
n
x
x
c
k
n
n
n
)
(
)
1
(
...
)
1
(
0
k
k
c
k
x
f
!
)
(
0
)
(
=
!
)
(
0
)
(
k
x
f
c
k
k
=
Stąd f(x)=
∑
∞
=
−
0
0
0
)
(
)
(
!
)
(
n
n
n
x
x
n
x
f
jest sumą swojego szeregu Taylora
•
1
0
0
1
)
(
)
(
0
+
∞
=
+
−
=
∫
∑
n
x
x
n
n
c
x
x
dt
t
f
n
szereg potęgowy można całkować wyraz po wyrazie

Automatyka i Robotyka –Analiza – Wykład 23 – dr Adam Ćmiel – cmiel@agh.edu.pl
5
Przykład. Znaleźć promień zbieżności i sumę wewnątrz przedziału zbieżności
∑
∞
=
+
0
4
)
3
(
n
n
n
n
x
(
0
,
4
)
3
(
1
0
=
+
=
x
n
a
n
n
)
4
1
4
1
4
)
3
(
1
lim
lim
=
=
⇒
=
+
=
=
∞
→
∞
→
α
α
R
n
a
n
n
n
n
n
n
dla
4
=
x
otrzymujemy szereg
∑
∞
=
+
0
)
3
(
1
n
n
- rozbieżny (harmoniczny)
dla
4
−
=
x
otrzymujemy szereg
∑
∞
=
+
−
0
)
3
(
)
1
(
n
n
n
- zbieżny (anharmoniczny)
Przedział zbieżności
)
4
,
4
[−
Promień zbieżności nie zmienia się po całkowaniu i różniczkowaniu szeregu potęgowego
(*)
3
0
4
)
3
(
1
)
(
x
x
n
x
S
n
n
n
⋅
+
=
∑
∞
=
dx
d
x
n
x
x
S
n
n
n
3
0
3
4
)
3
(
1
)
(
+
∞
=
∑
+
=
[
]
x
x
x
x
x
x
x
S
n
n
n
n
n
−
=
=
=
′
∑
∑
∞
=
+
∞
=
4
4
4
4
1
)
(
2
0
2
2
0
3
dla
4
<
x
/
∫
⋅
x
dt
0
)
(
x
x
x
S
x
x
S
−
+
−
−
=
−
4
4
2
3
3
ln
64
16
2
0
)
0
(
)
(
(
x
x
x
x
−
=
−
⇒
>
−
⇒
<
4
4
0
4
4
)
(**)
−
=
=
−
=
<
<
+
−
−
=
+
−
→
−
4
)
(
lim
2
ln
0
4
0
)
ln
64
16
2
(
)
(
4
2
1
3
1
4
4
2
1
3
x
x
S
x
x
x
x
x
S
x
x
x
tw.Abela
)
0
(
S
wyznaczamy wstawiając
0
=
x
do wzoru
∑
∞
=
+
=
0
4
)
3
(
1
)
(
n
n
n
x
n
x
S
i uwzględniając umowę
x
x
∀
= 1
0
(w szczególności
1
0
0
=
). Wobec tego
3
1
0
0
0
0
4
)
3
0
(
1
0
4
)
3
(
1
)
0
(
=
+
=
+
=
∑
∞
=
n
n
n
n
S
Uwaga 1. Umowa
x
x
∀
= 1
0
(w szczególności
1
0
0
=
) nie jest w sprzeczności z symbolem
nieoznaczonym
0
0
w którym zarówno podstawa potęgi jak i wykładnik zmierzają do 0. W naszym
przypadku
0
x
wykładnik jest równy 0 i mamy wiec zdefiniowaną funkcję stałą
0
x
=1 w sąsiedztwie
punktu 0. Punkt ten jest punktem nieciągłości usuwalnej, gdyż
1
lim
0
0
=
→
x
x
.
Uwaga 2. Suma szeregu potęgowego jest funkcją jednostajnie ciągła w każdym przedziale
domkniętym zawartym w przedziale zbieżności . Stąd
3
1
0
)
(
lim
)
0
(
=
=
→
x
S
S
x
Do wyznaczania wartości sumy szeregu w punkcie końcowym przedziału zbieżności wykorzystano
następujące
Tw. (Abela). Jeżeli szereg potęgowy jest zbieżny w punkcie końcowym przedziału zbieżności, to
jego suma jest funkcją jednostronnie ciągłą w tym punkcie.
Automatyka i Robotyka –Analiza – Wykład 23 – dr Adam Ćmiel – cmiel@agh.edu.pl
6
Uwaga. Jeżeli funkcja f jest postaci
∑
∞
=
−
=
0
0
)
(
)
(
n
n
n
x
x
c
x
f
,
R
x
x
<
−
|
|
0
przy czym promień
zbieżności jest dodatni ( czyli f jest analityczna w
)
,
(
0
0
R
x
R
x
+
−
, to jest ona funkcją klasy
∞
+
−
)
,
(
0
0
R
x
R
x
C
, tzn. ma wszystkie pochodne ciągłe w
)
,
(
0
0
R
x
R
x
+
−
.
Funkcja
=
≠
=
−
0
,
0
0
,
)
(
2
1
x
x
e
x
f
x
jest funkcją klasy
∞
R
C
, tzn. ma wszystkie pochodne ciągłe w R i
n
f
n
∀
= ,
0
)
0
(
)
(
stąd
)
(
0
!
)
0
(
0
)
(
x
f
x
n
f
n
n
n
≠
≡
∑
∞
=
. W tym przypadku funkcja f klasy
∞
R
C
nie jest sumą swojego szeregu Taylora, czyli nie jest funkcją analityczną. Jest tak dlatego, że
promień zbieżności R szeregu Taylora funkcji f jest równy 0.
Przykłady rozwinięć Taylora (Maclaurina)
L
+
+
+
+
+
+
=
=
∑
∞
=
!
5
!
4
!
3
!
2
1
!
5
4
3
0
2
x
x
x
x
x
k
x
e
k
k
x
,
R
x ∈
L
+
−
+
−
=
+
−
=
∑
∞
=
+
!
7
!
5
!
3
)!
1
2
(
)
1
(
sin
7
5
3
0
1
2
x
x
x
x
k
x
x
k
k
k
,
R
x ∈
L
+
−
+
−
=
−
=
∑
∞
=
!
6
!
4
!
2
1
)!
2
(
)
1
(
cos
6
4
2
0
2
x
x
x
k
x
x
k
k
k
,
R
x ∈
L
+
−
−
−
+
−
−
−
=
−
−
=
∑
∞
=
+
4
)
1
(
3
)
1
(
2
)
1
(
)
1
(
)
1
(
)
1
(
ln
4
3
2
1
1
x
x
x
x
k
x
x
k
k
k
,
1
|
1
|
<
−
x
Jeśli
A
jest macierzą kwadratową
n
n ×
o normie
A
, to korzystając z faktu, że zbieżność szeregu
(liczbowego) nom pociąga za sobą zbieżność szeregu w przestrzeni unormowanej możemy
zdefiniować funkcje macierzowe
L
+
+
+
+
+
+
=
=
∑
∞
=
!
5
!
4
!
3
!
2
!
5
4
3
0
2
A
A
A
A
A
I
k
A
e
k
k
A
,
L
+
−
+
−
=
+
−
=
∑
∞
=
+
!
7
!
5
!
3
)!
1
2
(
)
1
(
sin
7
5
3
0
1
2
A
A
A
A
k
A
A
k
k
k
,
L
+
−
+
−
=
−
=
∑
∞
=
!
6
!
4
!
2
)!
2
(
)
1
(
cos
6
4
2
0
2
A
A
A
I
k
A
A
k
k
k
,
L
+
−
−
−
+
−
−
−
=
−
−
=
∑
∞
=
+
4
)
(
3
)
(
2
)
(
)
(
)
(
)
1
(
ln
4
3
2
1
1
I
A
I
A
I
A
I
A
k
I
A
A
k
k
k
, gdy
1
|
1
|
<
−
j
λ
,
.
,
,
1
n
j
L
=
Problem. Jak efektywnie wyznaczać te (i inne) funkcje? Ponieważ każda macierz spełnia soje
równanie charakterystyczne, to wyższe potęgi macierzy A są liniowymi kombinacjami niższych potęg
i w konsekwencji powyższe szeregi redukują się do wielomianów macierzowych. Sposób
wyznaczania macierzy
At
e
zostanie omówiony przy okazji układów równań różniczkowych liniowych.
Wyszukiwarka
Podobne podstrony:
25 Szeregi potęgowe i ich zbieżność Własności sumy szeregu potęgowego
16 Rozdział 15 Szeregi potęgowe
AMI 24 Szeregi potęgowe
AM23 w04 Szeregi potęgowe
AM2 2 Szeregi potęgowe
8 szeregi potęgowe
Szeregi potęgowe, Matematyka
szeregi potęgowe
23 ciagi i szeregi funkcyjne 6 2 szeregi potegowe
25 Szeregi potęgowe i ich zbieżność Własności sumy szeregu potęgowego, Studia, Semestr VI, licencj
Szereg potegowy przyklady
Szereg potegowy przyklady ogarnijtemat.com, SiMR inżynierskie, Semestr 2, Równania różniczkowe, Wykł
Microsoft Word WE L13 szeregi potęgowe
16 Rozdział 15 Szeregi potęgowe
AMI 24 Szeregi potęgowe
Szeregi funkcyjne i potęgowe
więcej podobnych podstron