Całka powierzchniowa zorientowana
Niech S - gładki płat powierzchniowy.
Płat orientujemy czyli rozróżniamy jego strony: dodatnią ![]()
. W każdym punkcie płata zorientowanego prowadzimy wektor normalny ![]()
o zwrocie od strony ujemnej do dodatniej.
Orientacja płata S wyznacza jednoznacznie orientację krzywej ![]()
.
Krzywa K jest zorientowana dodatnio, gdy obiegając krzywą K zgodnie z orientacją wektor normalny mamy po stronie lewej.
Jeśli S jest powierzchnią zamkniętą, to przyjmujemy, że jej zewnętrzna strona jest stroną dodatnią; a wewnętrzna - ujemną.
Niech ![]()
- wersor normalny do płata S,
Ponieważ ![]()
, więc wersor normalny zadany jest wzorem
![]()
, gdzie ![]()
są kątami między wektorem ![]()
a dodatnimi półosiami ![]()
.
Niech ![]()
- pole wektorowe określone na płacie S,
![]()
,
oraz niech
![]()
.
W każdym punkcie płata S tworzymy iloczyn skalarny
![]()
Wartość tego iloczynu jest długością rzutu wektora ![]()
na prostą normalną bo ![]()
.
Ponieważ
![]()
całka powierzchniowa niezorientowana
Definicja
Całką powierzchniową niezorientowaną funkcji ![]()
czyli
![]()
nazywamy całkę powierzchniową zorientowaną funkcji wektorowej ![]()
na płacie zorientowanym S i oznaczamy symbolem
![]()
Uwaga
![]()
Jeśli zmienimy orientację płata S na przeciwną, to
czyli
![]()
Definicja
Całkę powierzchniową zorientowaną nazywamy też strumieniem pola wektorowego ![]()
przez powierzchnię S.
Niech S - powierzchnia regularna, tzn. powierzchnia jest sumą płatów gładkich ![]()
.
Uwaga
Istnieją powierzchnie jednostronne (np. wstęga Mbiusa)
Zatem nie każdą powierzchnię regularną można zorientować.
Definicja
Niech ![]()
powierzchnia regularna dwustronna,
![]()
, gdzie![]()
płat gładki dla ![]()
Wtedy
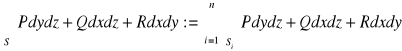
Uwaga
![]()
bo
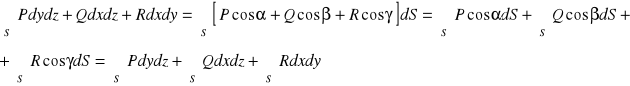
Twierdzenie 1
Niech ![]()
płat powierzchniowy zorientowany
![]()
![]()
Wtedy ![]()
całka powierzchniowa po górnej stronie płata S :
![]()
,
![]()
całka powierzchniowa po dolnej stronie płata S :
![]()
Dowód
Ponieważ płat S zadany jest w postaci jawnej ![]()
, więc wektor normalny jest postaci
![]()
lub ![]()
.
![]()
Niech ![]()
Wtedy ![]()
oraz
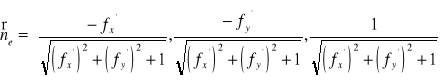

![]()
Dowodzimy analogicznie.
Twierdzenie 2
Niech: ![]()
płat powierzchniowy zorientowany
![]()
![]()
Wtedy ![]()
-całka powierzchniowa po górnej stronie płata S :
![]()
![]()
-całka powierzchniowa po dolnej stronie płata S :
![]()
Twierdzenie 3
Niech: ![]()
płat powierzchniowy zorientowany
![]()
![]()
Wtedy ![]()
-całka powierzchniowa po górnej stronie płata S :
![]()
![]()
-całka powierzchniowa po dolnej stronie płata S :
![]()
Przykład
Obliczyć całkę ![]()
po zewnętrznej stronie powierzchni
![]()
.
Rozłóżmy całkę I na sumę trzech całek
![]()
, gdzie
![]()
![]()
![]()
i dla całki ![]()
skorzystajmy z ??????, gdzie ![]()
.
![]()
Powierzchnia S jest płatem powierzchniowym zadanym równaniem ![]()
, gdzie ![]()
. Stąd
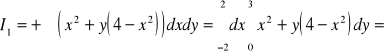
![]()
![]()
- bo rzut powierzchni S jest krzywą ![]()
(a nie obszarem).
![]()
![]()
Rzutujemy S na płaszczyznę ![]()
. Rzut ![]()
powstaje z rzutowania zarówno części powierzchni S dla której ![]()
oraz z tej części S dla której ![]()
. Rozłóżmy zatem S na sumę
![]()
,
gdzie
![]()
oraz
![]()
.
wtedy
![]()
Z ![]()
,![]()
,![]()
otrzymujemy ![]()
………………………
![]()
Przykład
Obliczyć całkę
gdzie S jest zewnętrzną stroną powierzchni sfery
![]()
I sposób.
Oczywiście ![]()
Wystarczy więc obliczyć tylko jedną z tych całek, np. ![]()
Sferę S rozbijamy na dwie półsfery: górną (względem płaszczyzny OXY) ![]()
i dolną ![]()
; a następnie korzystamy z twierdzenia.
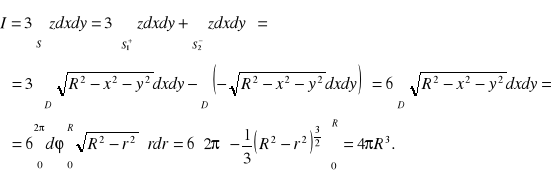
II sposób.
Tym razem skorzystamy z definicji całki powierzchniowej zorientowanej, a następnie z twierdzenia o zamianie całki powierzchniowej niezorientowanej na całkę podwójną.
![]()
Sfera S ma następującą parametryzację:
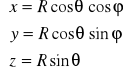
, gdzie ![]()
i wtedy wektor normalny jest postaci
![]()
dla ![]()
gdzie![]()
Stąd
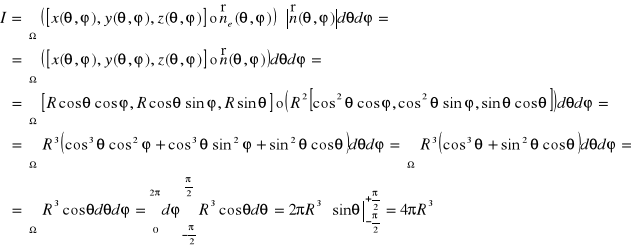
Twierdzenie
Jeśli płat powierzchniowy S zadany jest równaniami parametrycznymi
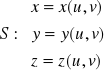
, gdzie ![]()
,
oraz
![]()
,
to
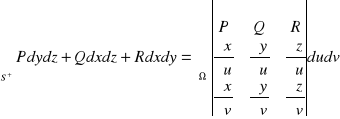
.
Dowód
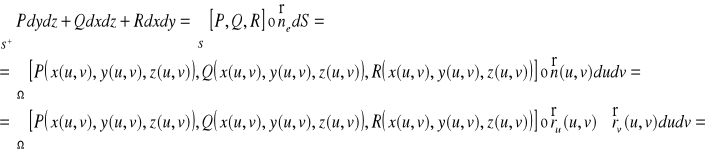
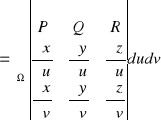
Twierdzenie (Stokesa)
Jeżeli ![]()
, gdzie S jest dwustronną
powierzchnią gładką ograniczoną krzywą regularną przestrzenną zamkniętą K,
oraz
orientacja powierzchni S jest zgodna z orientacją krzywej![]()
,
to
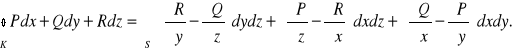
Uwaga
Jeśli powierzchnia S jest płaskim obszarem w płaszczyźnie OXY, to ![]()
, i z twierdzenia Stokesa otrzymujemy twierdzenie Greena.
Twierdzenie (Gaussa - Ostrogradskiego)
Jeśli S - powierzchnia zamknięta ograniczająca obszar przestrzenny V
oraz
pole wektorowe ![]()
,
to
![]()
.
Teoria pola
Niech
![]()
- obszar przestrzenny, ![]()
;
![]()
- pole skalarne, ![]()
;
![]()
- pole wektorowe, ![]()
.
Wektorowym operatorem różniczkowym (operatorem Hamiltona) nazywamy symboliczny wektor ![]()
,
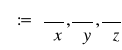
.
Korzystając z symbolu ![]()
łatwo podać definicje funkcji pola skalarnego F i wektorowego ![]()
:
gradient pola F
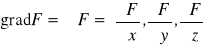
,
dywergencja pola
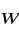
![]()
rotacja pola
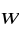
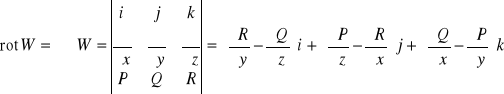
Niech S - powierzchnia dwustronna,
![]()
.
Strumieniem pola wektorowego ![]()
przez powierzchnię S w kierunku wersora ![]()
nazywamy całkę powierzchniową zorientowaną
![]()
Niech K - krzywa zamknięta
![]()
Cyrkulacją pola ![]()
wzdłuż krzywej zamkniętej K nazywamy całkę krzywoliniową skierowaną
![]()
, gdzie![]()
- wersor styczny do krzywej K
skierowany zgodnie z tą krzywą.
Wzór Stokesa
![]()
, gdzie krzywa K i powierzchnia S mają
zgodną orientację.
Wzór Gaussa - Ostrogradskiego
![]()
.
Definicja
Niech ![]()
,
![]()
.
Pole wektorowe ![]()
nazywamy polem potencjalnym, gdy ![]()
, ![]()
.
Funkcję U nazywamy potencjałem skalarnym pola wektorowego ![]()
.
Jeśli V - jednospójny powierzchniowo, to
![]()
- potencjalne ![]()
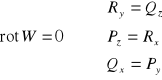
Ponadto potencjał U wyznaczamy ze wzoru
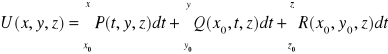
,
gdzie ![]()
jest ustalonym punktem, ![]()
Przykład
Obliczyć pracę wykonaną przez siłę![]()
działającą wzdłuż obwodu trójkąta ABC o wierzchołkach A(1,0,0), B(0,1,0), C(0,0,1).
Praca ![]()
Aby skorzystać z twierdzenia Stokesa wyznaczmy wersor normalny do trójkąta ABC. Płaszczyzna zawierająca ten trójkąt ma równanie
![]()
,
a więc wektor normalny oraz wersor normalny mają współrzędne:
![]()
, 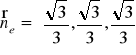
.
Ponadto
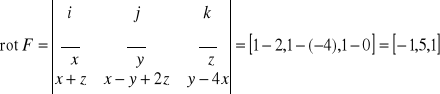
.
Zatem
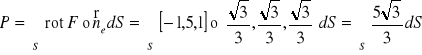
,
gdzie
![]()
przy czym D jest rzutem ABC na płaszczyznę OXY.
Stąd zamieniając całkę powierzchniową niezorientowaną na całkę podwójną otrzymujemy
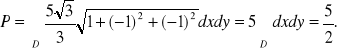
![]()
![]()
Wyszukiwarka
Podobne podstrony:
Calka powierzchniowa zorientowana
4. całka powierzchniowa zorientowana
calka powierzchniowa zorientowana
3.Całka powierzchniowa zorientowana, MATEMATYKA, CAŁKI, CAŁKI KRZYWOLINIOWE I POWIERZCHNIOWE, 02Całk
Calka powierzchniowa zorientowana
całka powierzchniowa niezorientowana
calka powierzchniowa III i analiza wektorowa
3. całka powierzchniowa niezorientowana
Calka powierzchniowa skalarna
calka powierzchniowa II
calka powierzchniowa I
3 całka powierzchniowa niezorientowana
calka powierzchniowa niezorient Nieznany (2)
Całki powierzchniowe zorientowane
całka powierzchniowa niezorientowana
więcej podobnych podstron







