Właściwości 

sprężyste 

materiałów

wielofazowych

Kamil Kos

2

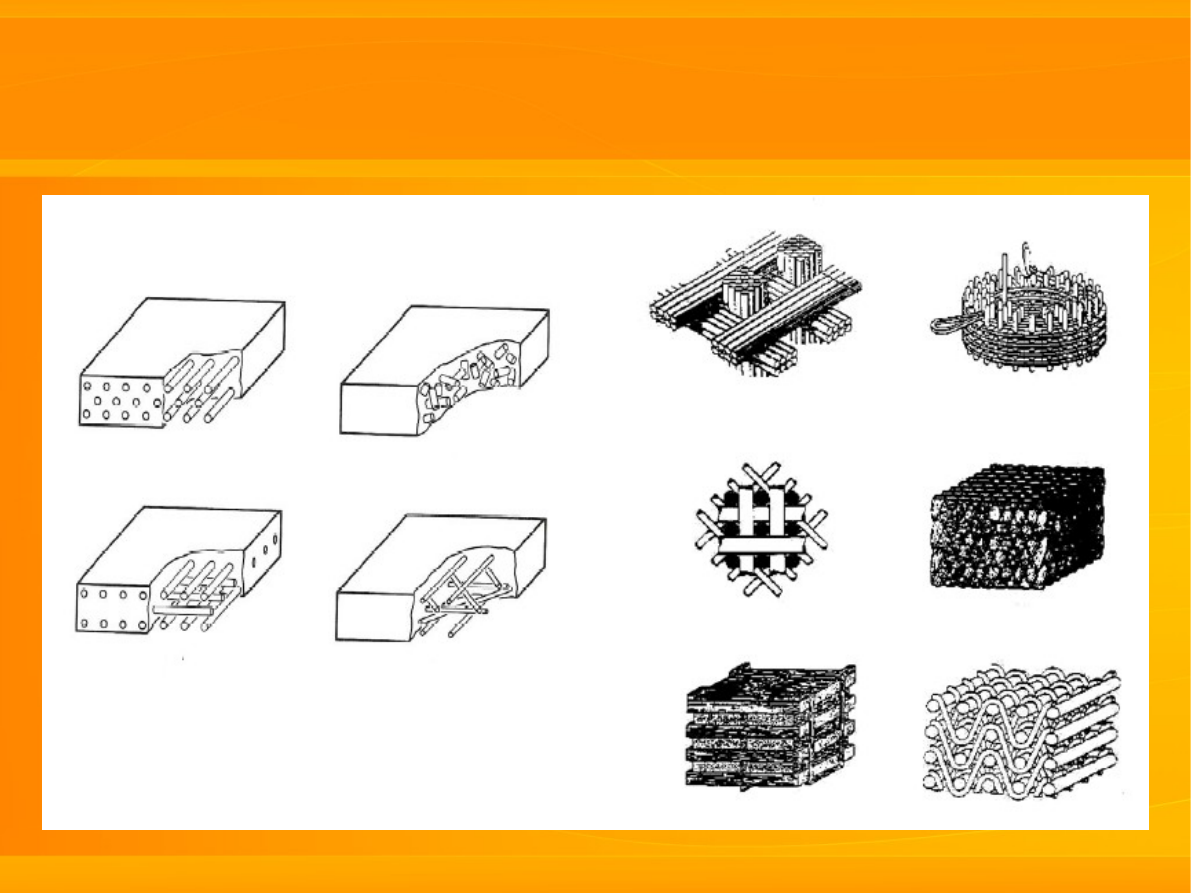
1. Kompozyty

a) wzmacniane włóknami
b) wzmacniane cząstkami
c) porowate

3

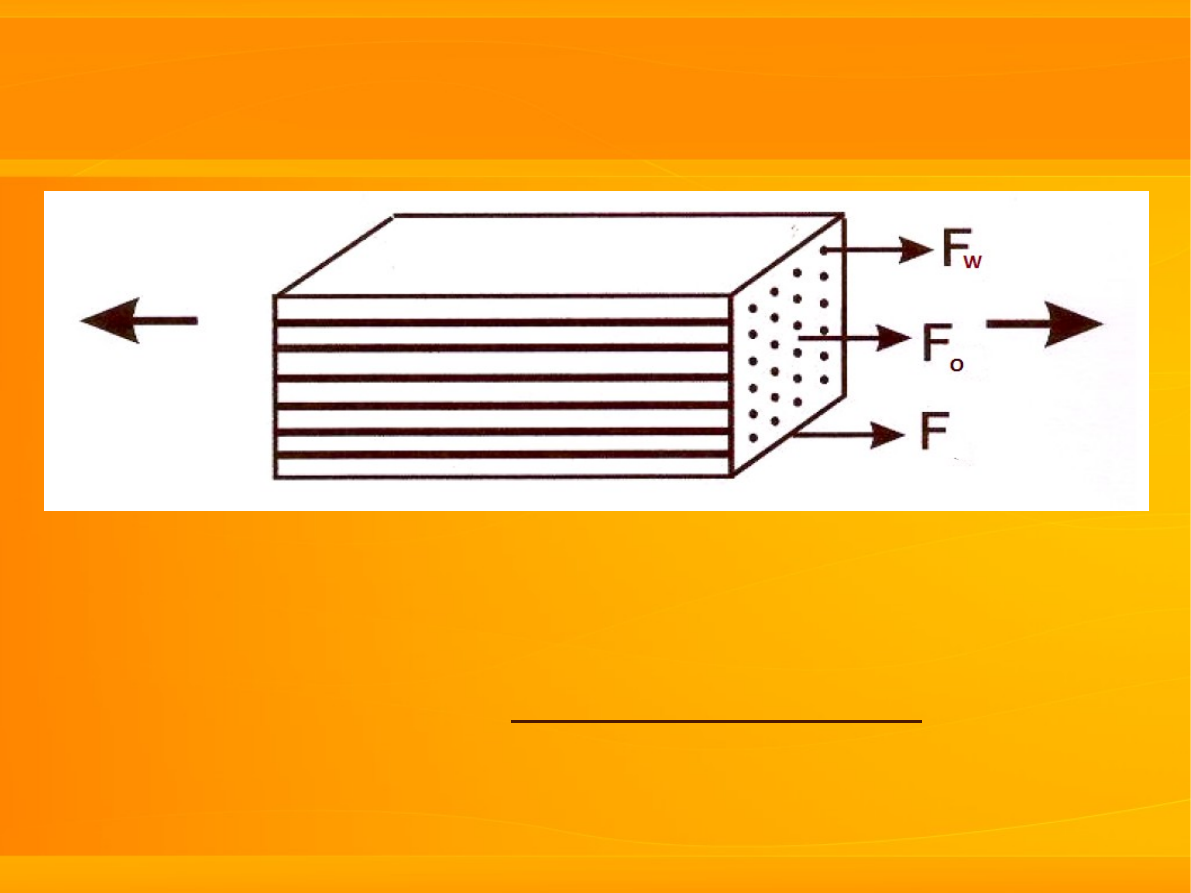
a) kompozyty wzmacniane włóknami

Model równoległy    

założenia:

□

ε = ε

o

 = ε

w

□

ν = ν

o

 = ν

w

□

włókna jednorodne, ciągłe, 

ułożone w kierunku działania siły F

□

idealne połączenie osnowy i 

włókien

4

a) kompozyty wzmacniane włóknami

F = F

o

 + F

w

    σ = σ

w

V

w 

+ σ

o

V

o             

σ=

ε

E

E = E

w

V

w

 + E

o

V

o 

reguła mieszanin

5

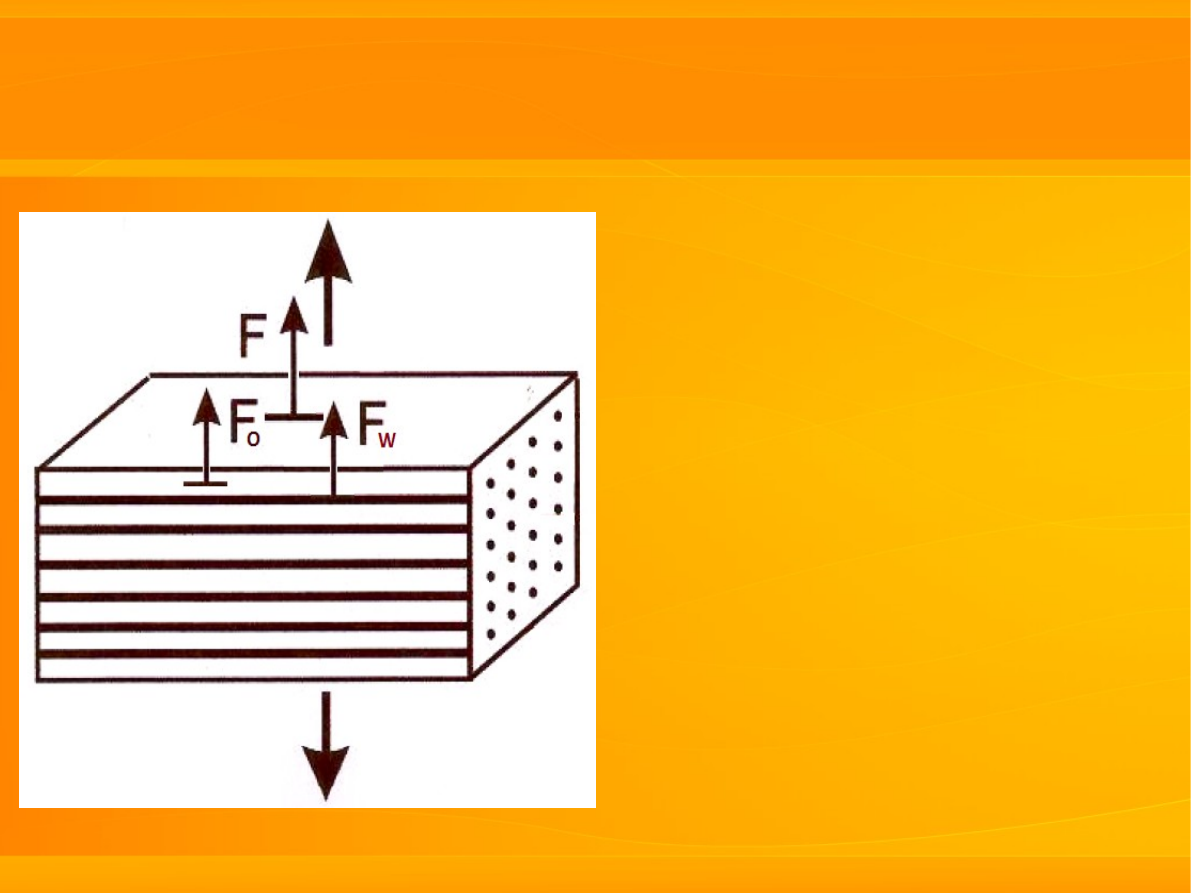
a) kompozyty wzmacniane włóknami

Model szeregowy    

założenia:

□

ε ≠ ε

o

 ≠ ε

w

□

σ = σ

o

 = σ

w

  

6

a) kompozyty wzmacniane włóknami

ε = ε

w

V

w 

+ ε

o

V

o 

1 / E = V

1

 / E

1

 + V

2 

/ E

2

7

b) kompozyty wzmacniane cząstkami

□

średnica cząstek > 1 um

□

wprowadzanie do osnowy cząstek o 

twardości i sztywności większej od 

twardości i sztywności osnowy

□

mechanizm polega na zmniejszaniu przez 

cząstki fazy rozproszonej odkształceń 

osnowy

□

wartość wzmocnienia trudna do 

przewidzenia

□

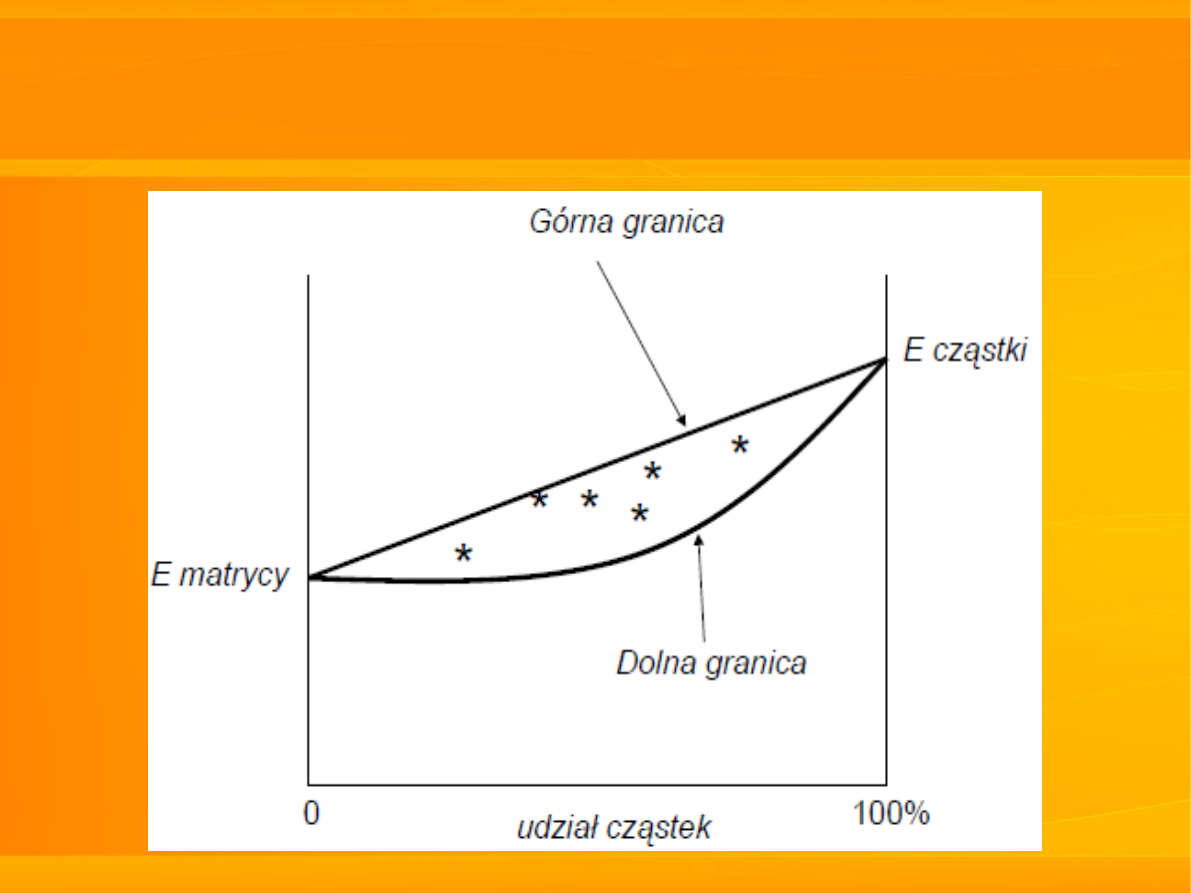
do wyznaczenia modułu Younga stosuje się 

model szeregowy

8

b) kompozyty wzmacniane cząstkami

9

b) kompozyty wzmacniane cząstkami

□

wzmocnienie dyspersyjne

□

średnica cząstek w zakresie od 0,01 

do 0,1 um

□

cząstki mają za zadanie utrudnić 

rozchodzenie się dyslokacji poprzez 

ich wygięcie i  zamknięcie

□

poprawiona odporność na pełzanie

10

c) kompozyty porowate

□

dla gazu można przyjąć, że E

g

 = 0

□

V

s

 = 1- V

g

 

□

z reguły mieszanin:

E = E

s

 (1 – V

g

) 

E

s

 – moduł Younga fazy stałej

V

g

 – udział objętościowy porów  

11

c) kompozyty porowate

W rzeczywistości pory powodują 

koncentracje naprężeń, czyli zwiększenie 

gęstości zmagazynowanej energii 

odkształcenia sprężystego w niewielkiej 

odległości od danej nieciągłości. 

k – współczynnik koncentracji naprężeń

  

np. dla porów eliptycznych    k = (5/4)(a/c)+(3/4)

gdzie:

a – długość poru w płaszczyźnie prostopadłej do wektora naprężenia 

c - długość poru w płaszczyźnie równoległej do wektora naprężenia

E = E

s

 (1 – k·V

g

)  

12

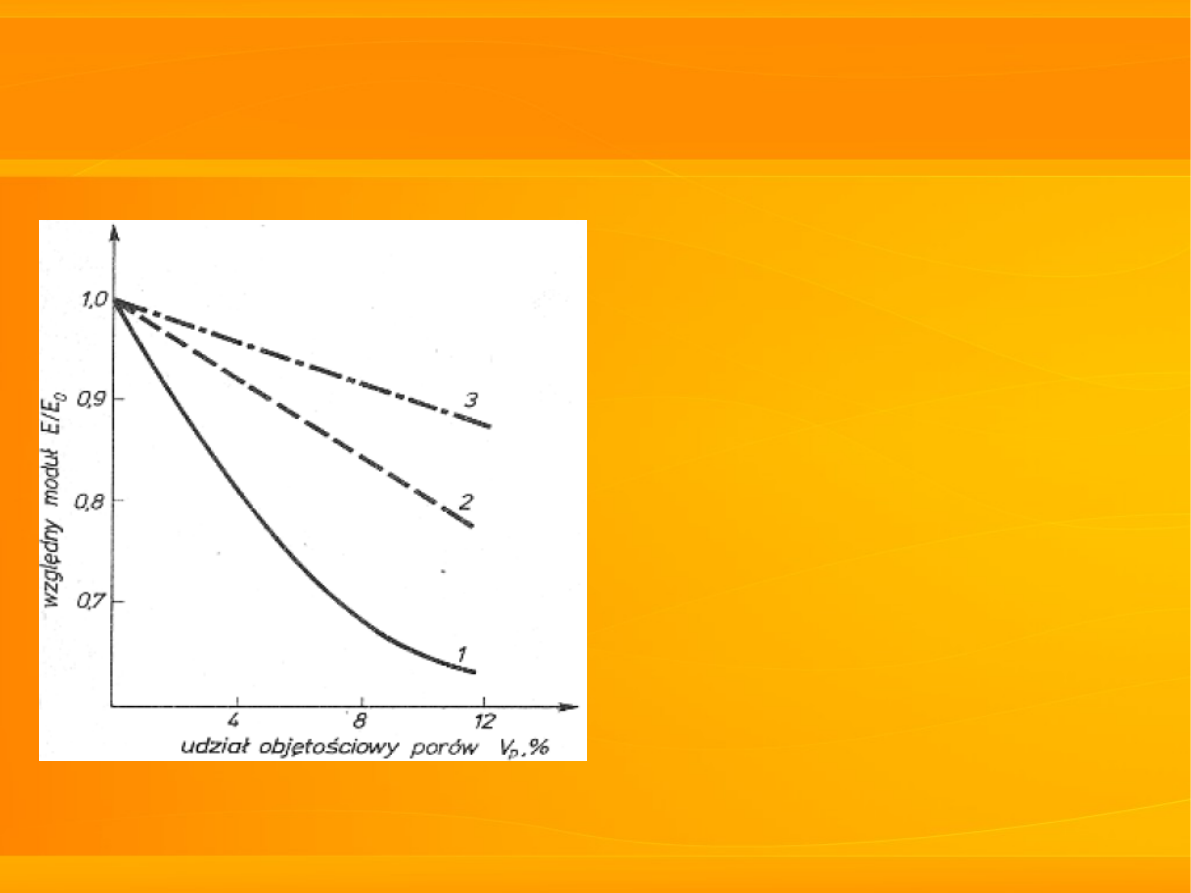
c) kompozyty porowate

Stosunek modułów 

Younga: 

porowatego E i 

nieporowatego E

0

1. dane doświadczalne – 

większy spadek związany 

z obecnością porów 

niekulistych

2. dla porów kulistych

3. wyliczone z prawa 

mieszanin

13

c) kompozyty porowate

□

Kompozyty piankowe

E = E

p

 (ρ/ρ

p

)

2

       

E - moduł Younga pianki
E

p

 - moduł Younga polimeru

ρ - gęstość pianki
ρ

p –

 gęstość polimeru

14

Odstępstwa od prawa mieszanin

□

ε ≠ ε

o

 ≠ ε

w

□

ν ≠ ν

o

 ≠ ν

w

□

nierównoległość ułożenia włókien

□

włókna nieciągłe

□

różne współczynniki 

rozszerzalności cieplnej

15



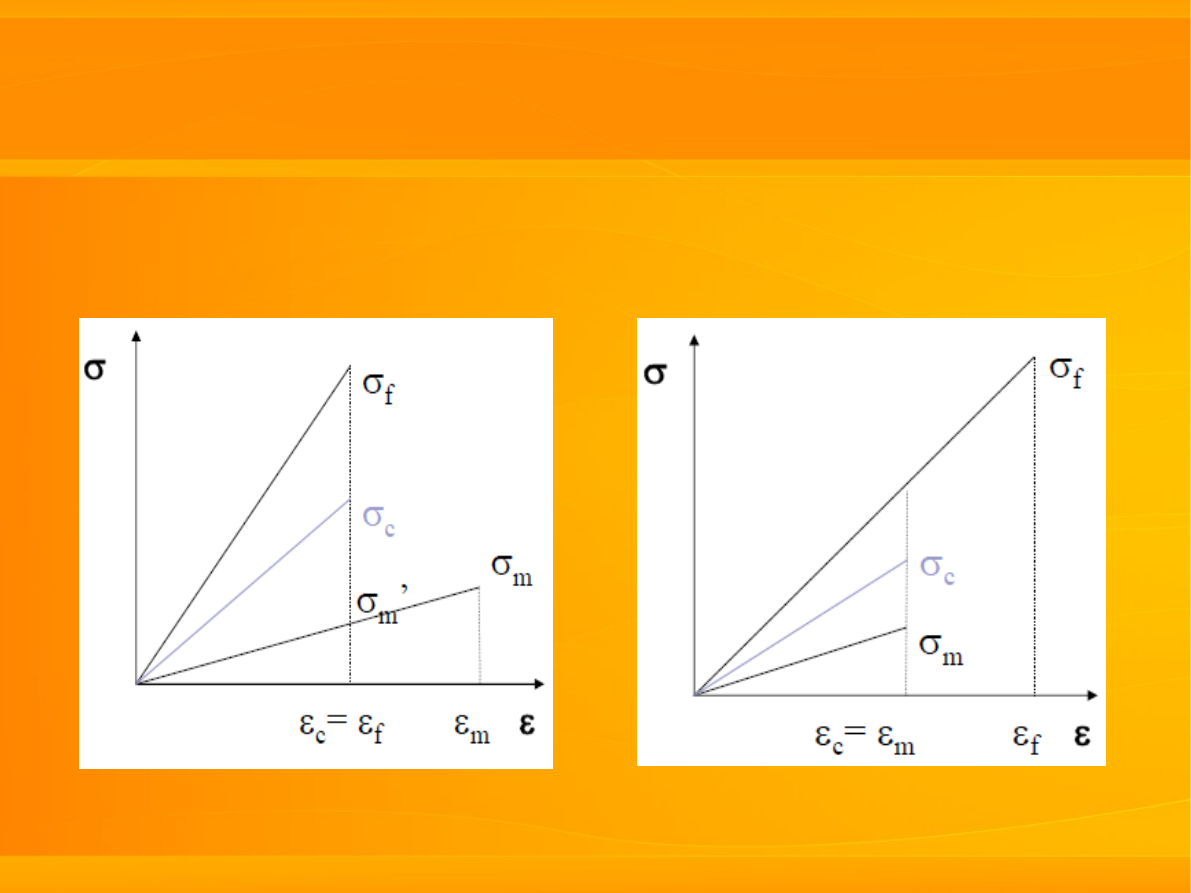
 ε ≠ ε

o

 ≠ ε

w

□

osnowa 

plastyczna

□

osnowa krucha

16



 nierównoległość ułożenia 

włókien

17



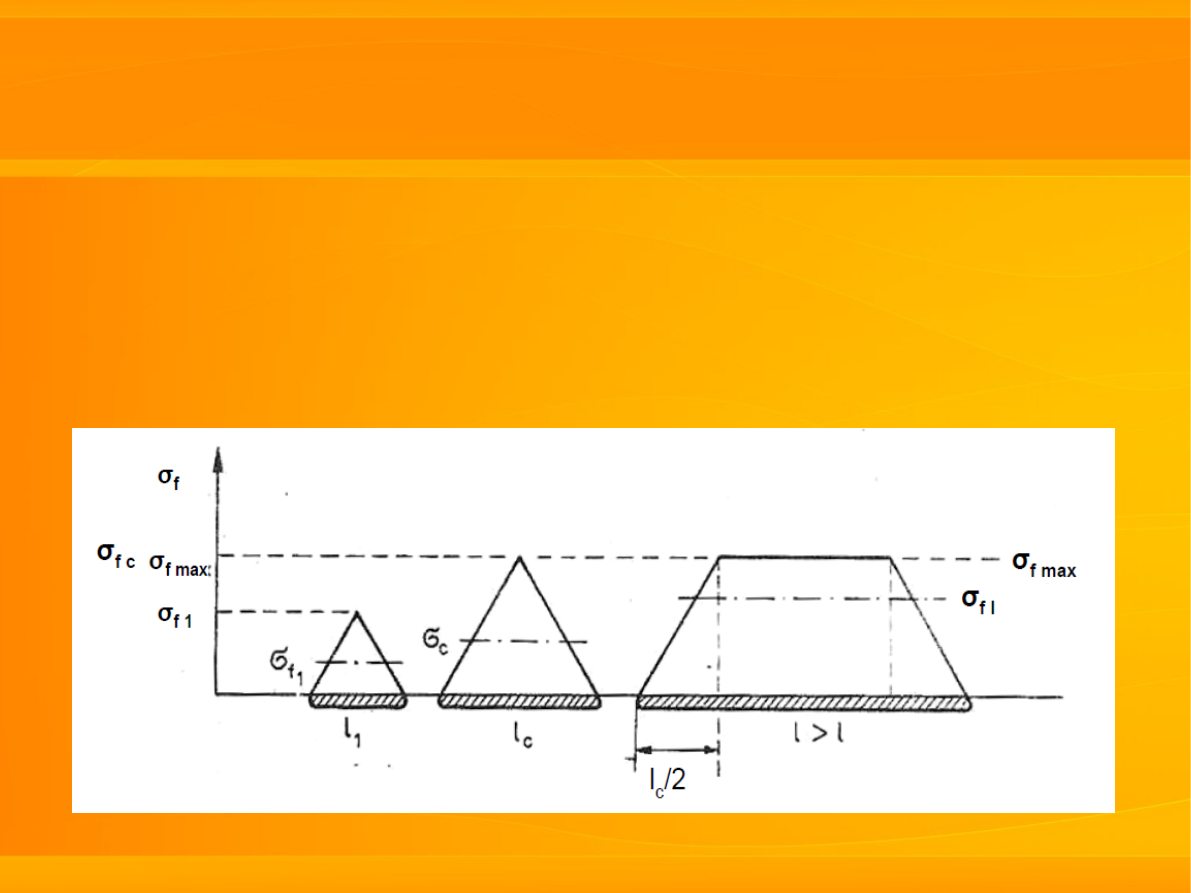
 włókna nieciągłe

□

obciążenia są przenoszone przez 

powierzchnię kontaktu włókna z 

osnową

□

długość krytyczna włókien

 

18



 różne współczynniki 

rozszerzalności cieplnej

□

α

o

 < α

w

 - spękanie osnowy

□

α

o

 > α

w 

- odrywanie włókna od 

                     osnowy

19

Anizotropia modułu Younga i σ

□

zależnie od sposobu produkcji 

materiały wielofazowe cechują się 

różną anizotropią właściwości 

sprężystych

20

Anizotropia modułu Younga i σ

□

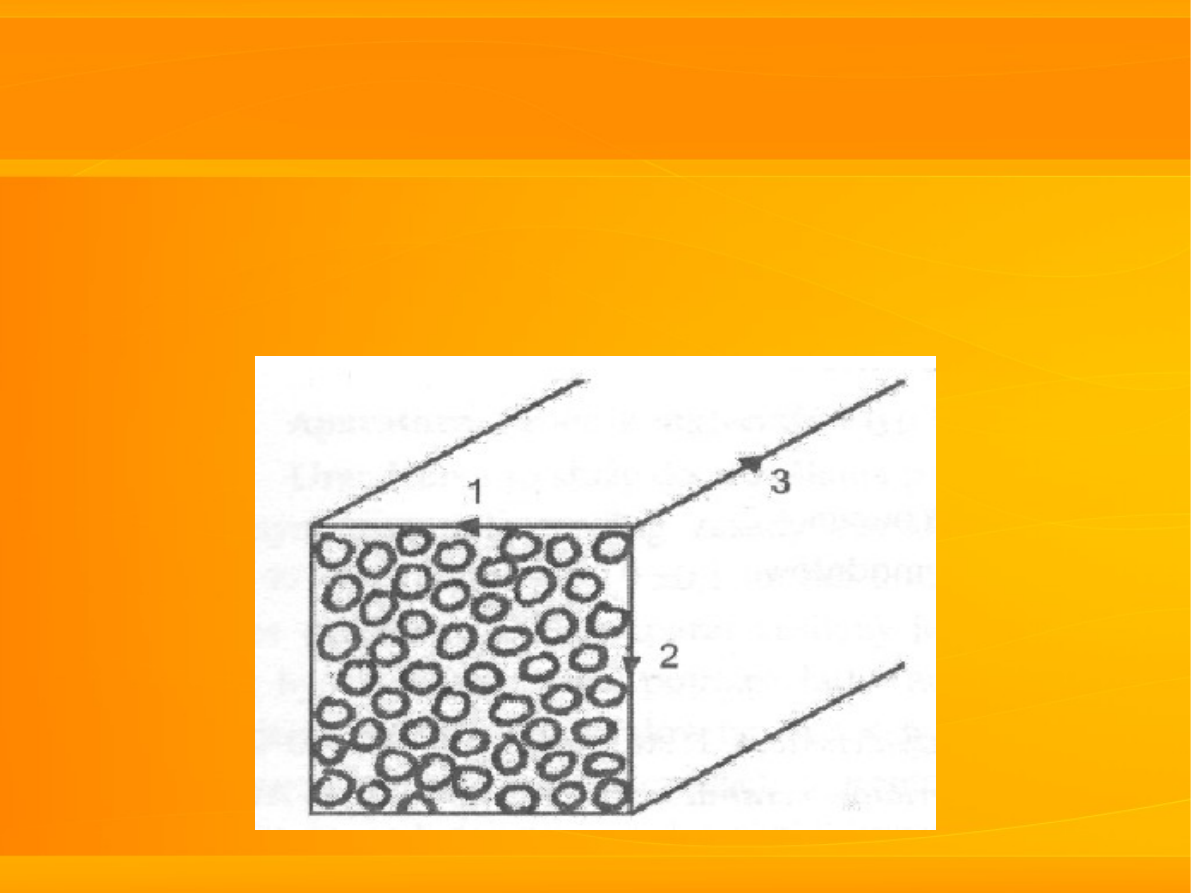
w przypadku materiału porowatego 

formowanego przez wyciąganie:

21

Anizotropia modułu Younga i σ

□

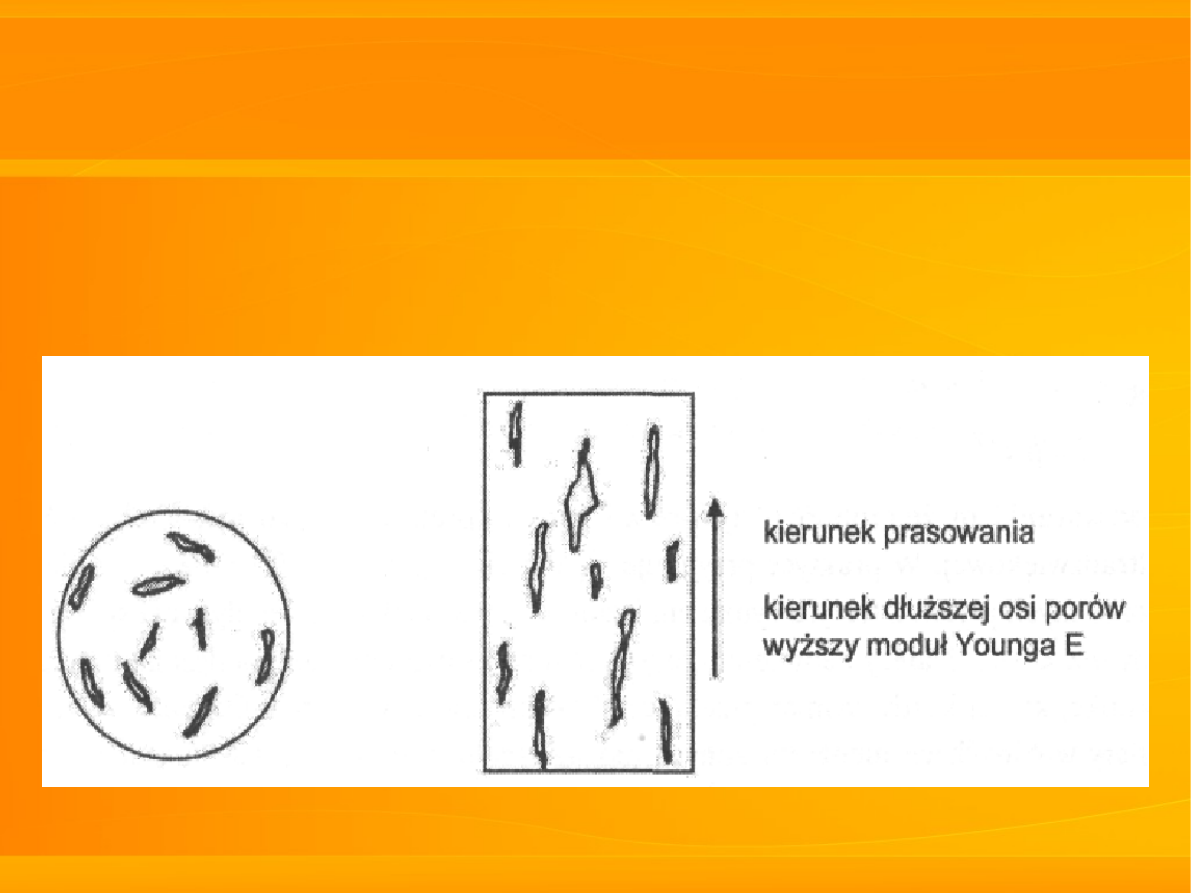
w przypadku materiału porowatego 

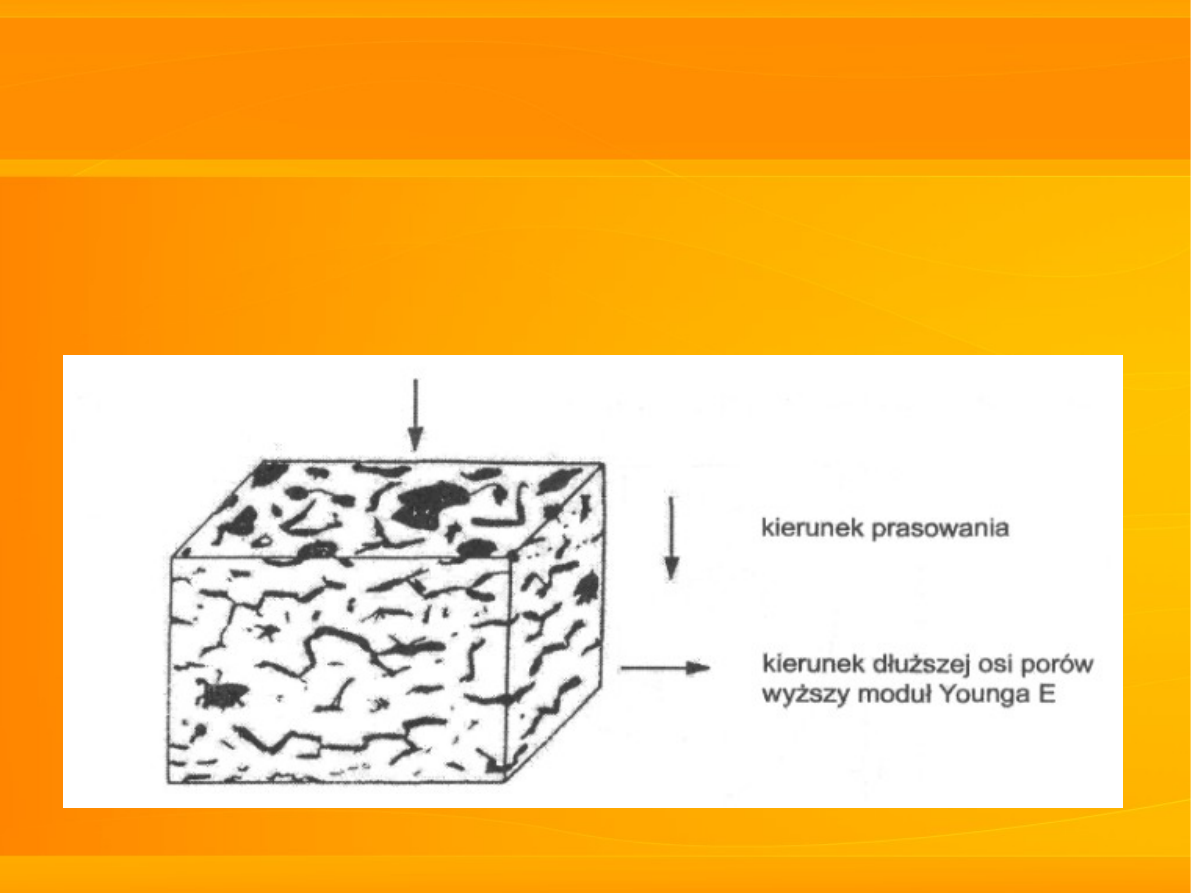
formowanego przez prasowanie: 

22

Anizotropia modułu Younga i σ

□

w przypadku kompozytu 

formowanego przez prasowanie i 

wyciąganie:

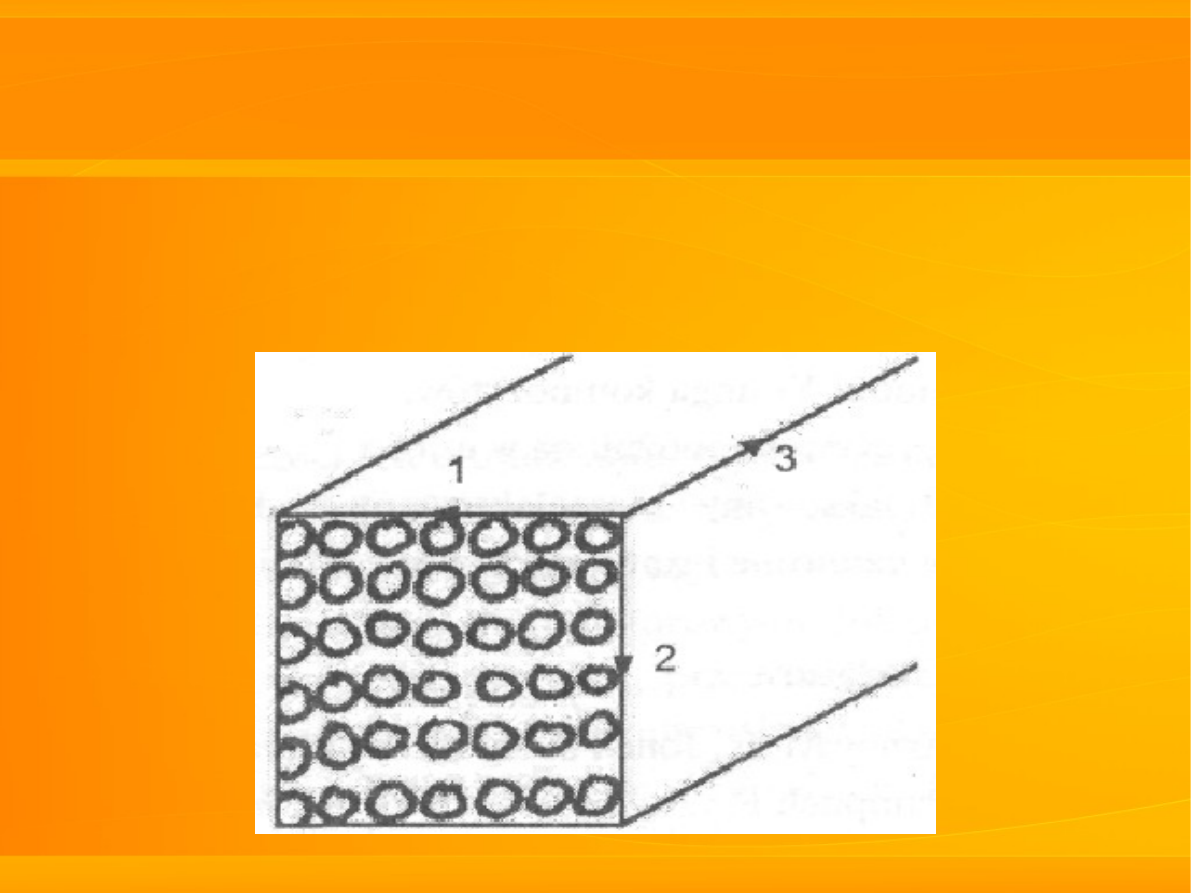
23

Anizotropia modułu Younga i σ

□

w przypadku kompozytu 

formowanego przez sklejanie 

warstw:

24

Anizotropia modułu Younga i σ

Opis matematyczny:      (σ

i

) = (C

ij

)·(ε

j

)

25

Koniec