Seria: Informatyka
Metody niezawodności i
eksploatacji
Wykład 12
Kontrola stanu i lokalizacja
uszkodzeń
dr hab. inż. Tadeusz Nowicki prof.
nadzw. WAT
e-mail:nowicki@isi.wat.edu.pl, tel. 6-
837118
Seria: Informatyka
Metody niezawodności i
eksploatacji
Wykład 12
Kontrola stanu i lokalizacja
uszkodzeń
dr hab. inż. Tadeusz Nowicki prof.
nadzw. WAT
e-mail:nowicki@isi.wat.edu.pl, tel. 6-
837118
1. Podstawy kontroli systemów technicznych
W ramach teorii eksploatacji rozpatruje się między
innymi
profilaktykę,
kontrolę
i
lokalizację
uszkodzeń
w
odniesieniu
do
systemów
technicznych. Profilaktykę systemów technicznych
omówiliśmy na poprzednich wykładach. Teraz
zajmiemy się problemami kontroli systemów
technicznych. Wykład dotyczyć będzie omówienia
metod powodujących znajomość stanu obiektu
technicznego. Nie można w sposób ciągły
kontrolować stanu systemu. Informacji o stanie
systemu
dostarczać
więc
powinny
kontrole
wyrywkowe. Przeprowadzenie kontroli wymaga
pewnych nakładów, zatem sposób organizacji
procesu kontroli jest problemem samym w sobie.
Sporządza się tak zwany plan kontroli systemu.
Jego konstrukcja zależy silnie od własności samego
systemu. W praktyce szczególną role mają tzw.
sztywne plany kontroli polegające na wyznaczeniu
ustalonych
chwil
kontroli.
Plan
kontroli
scharakteryzowany będzie wtedy jednoznacznie
ciągiem liczb S=(t
1
, t
2
,..., t
k
), gdzie t
k
oznacza
chwilę k-tej kontroli.
1.1. Kontrola obiektów nienaprawialnych.
Przyjmijmy założenia:
-informacje o stanie systemu uzyskać możemy
tylko w wyniku kontroli,
-czas trwania kontroli jest pomijalnie mały,
-w czasie trwania kontroli system nie ulega
uszkodzeniom,
-koszt każdej kontroli wynosi C
1
,
-straty wywołane uszkodzeniem systemu są
proporcjonalne do czasu pracy obiektu z nie
wykrytym uszkodzeniem, a koszt na jednostkę
czasu wynosi C
2
,
-eksploatacja systemu kończy się wraz z
uszkodzeniem systemu.
Oznaczmy przez N(t) liczbe kontroli w
przedziale czasu (0,t) i przez Y
t
przedział czasu
między powstaniem uszkodzenia, a jego
wykryciem pod warunkiem, że uszkodzenie
nastąpiło w chwili t.
Wtedy łączny koszt jego eksploatacji
wyniesie:
t
2
1
Y
C
1
)
t
(
N
C
Gdzie pierwszy składnik oznacza koszt wszystkich
N(t)+1
kontroli,
a
drugi
koszt
pracy
uszkodzonego systemu w czasie Y
t
.
Jeśli znany jest rozkład F(t) czasu pracy
bezawaryjnej systemu, to wartość oczekiwaną
strat można wyznaczyć następująco:
)
t
(
dF
EY
C
1
)
t
(
EN
C
C
0
t
2
1
przy czym EN(t) jest wartością oczekiwana
liczby kontroli do chwili uszkodzenia, EY
t
jest wartością oczekiwaną czasu pracy
uszkodzonego obiektu.
Określenie optymalnej strategii kontroli polega
na wyznaczeniu takich chwil t
1
< t
2
<...< t
k
<... (być
może losowych, w których należy przeprowadzić
kontrolę tak, aby koszt C był minimalny. W
sytuacji, w której chwile przeprowadzenia
kontroli nie są zmiennymi losowymi, wartość
oczekiwaną kosztów można wyznaczyć ze wzoru:
0
k
1
k
t
k
t
1
k
2
1
)
t
(
dF
)
t
t
(
C
)
1
k
(
C
C
Można pokazać, że jeśli F(t) jest ciągła ze
skończona wartością oczekiwaną, to istnieje
optymalna strategia kontroli. Dowodzi się,
ze gdy F(t)=1 dla tT i jeśli
T
t
0
dla
)
t
T
)(
C
/
C
(
1
1
)
t
(
F
2
1
(1
)
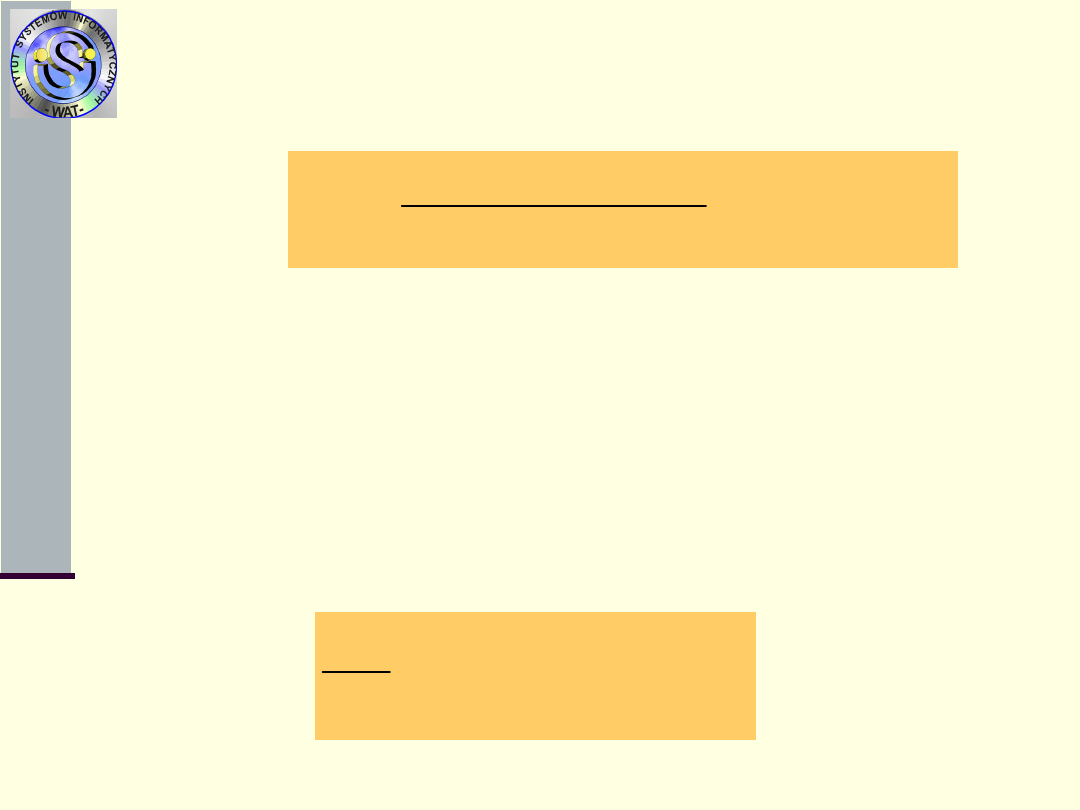
To optymalna strategia kontroli polega na
przeprowadzeniu pojedynczej kontroli w chwili
T,
jeśli
natomiast
istnieje
takie
0t T, że
T
t
0
dla
)
t
T
)(
C
/
C
(
1
1
)
t
(
F
2
1
To optymalna strategia kontroli wymaga
przeprowadzenia dodatkowo co najmniej jednej
kontroli w rozpatrywanym przedziale czasu.
Załóżmy ponadto, że F(t) jest różniczkowalna, a
f(t)=F’(t) jest gęstością Polyi rzędu 2 (funkcja
f(t) jest określona w przedziale (-, ) o
wartościach rzeczywistych i intensywność awarii
jest stale monotonicznie rosnąca). Optymalna
strategia kontroli spełnia warunki
,...
2
,
1
k
dla
0
t
C
k
2
1
k
1
k
k
k
1
k
C
C
)
t
(
f
)
t
(
F
)
t
(
F
t
t
Uwzględniając zatem zależność (1)
otrzymamy dla k=1,2,..., że
Jeżeli f(t
k
)=0, to
t
k+1
- t
k
= i dalsze kontrole są
niepotrzebne. Po ustaleniu t
1
>0 można
obliczyć t
2
, t
3
,... Rekurencyjnie wykorzystując
wzór (2). Tym samym problem określenia
optymalnej strategii {t
k
*} sprowadza się do
wyznaczenia t
1
*.
W
pewnym
uproszczeniu
algorytm
wyznaczania optymalnego planu kontroli jest
następujący:
• wyznaczyć t
1
ze wzoru (2)
• rekurencyjnie wyznaczyć chwile kontroli t
2
,
t
3
,..., t
k
... .
(2)
1.2. Kontrola obiektów naprawialnych.
Zakładaliśmy, że okres eksploatacji kończył
się wraz z wykryciem uszkodzenia, a
kryterium jakości był łączny koszt całego
okresu eksploatacji. W przypadku obiektów
naprawialnych, bezpośrednio po wykryciu
uszkodzenia przystępuje się do odnowy
systemu
przywracając
go
do
pełnych
własności eksploatacyjnych.
Przyjmijmy, że C
1
jest kosztem pojedynczej
kontroli, C
2
jednostkowym kosztem pracy
uszkodzonego systemu, a
C
3
kosztem
pojedynczej odnowy. Przy przyjętej strategii
kontroli Z=(
t
1
,t
2
,...,t
k
) średnie koszty na cykl
wyniosą zgodnie z (1):
3
0
k
1
k
t
k
t
1
k
2
1
C
)
t
(
dF
)
t
t
(
C
)
1
k
(
C
)
Z
(
C
(3
)
Średnia długość cyklu wyniesie:
R
0
k
1
k
t
k
t
1
k
FF
T
)
t
(
dF
)
t
t
(
T
)
Z
(
T
gdzie
T
FF
jest
średnim
czasem
pracy
bezawaryjnej, zaś T
R
średnim czasem odnowy
systemu. Srednie jednostkowe straty przy t
wynoszą:
)
Z
(
T
)
Z
(
C
)
Z
(
K
W
dalszym
ciągu
założymy, że
2
R
FF
3
1
C
T
T
C
C
to znaczy, że koszt jednostkowy wynikający z
idealnej kontroli (uszkodzenie wykrywane
natychmiast) i odnowy nie przewyższają kosztu
jednostkowego
wynikającego
z
pracy
uszkodzonego
systemu.
W
przeciwnym
przypadku kontrole i odnowy nie miałyby sensu
W celu sformułowania optymalnej strategii
kontroli wprowadzimy najpierw wielkość
pomocniczą:
)
Z
(
aT
)
Z
(
C
)
Z
,
a
(
D
Wynika stąd naturalnie
)
T
T
(
a
C
)
t
(
dF
)
t
t
)(
a
C
(
)
1
k
(
C
)
Z
,
a
(
D
R
FF
3
0
k
1
k
t
k
t
1
k
2
1
(4
)
Niech Z(a) będzie strategia minimalizującą
D(a,Z). Jeżeli spełnione są warunki drugiej
własności strategii optymalnej, to można
wyznaczyć Z(a) za pomocą podanego poprzednio
algorytmu.
Tym
razem
jednak
warunki
konieczne do tego, aby funkcja D(a,Z) miała
minimum względem Z, maja postać:
,...
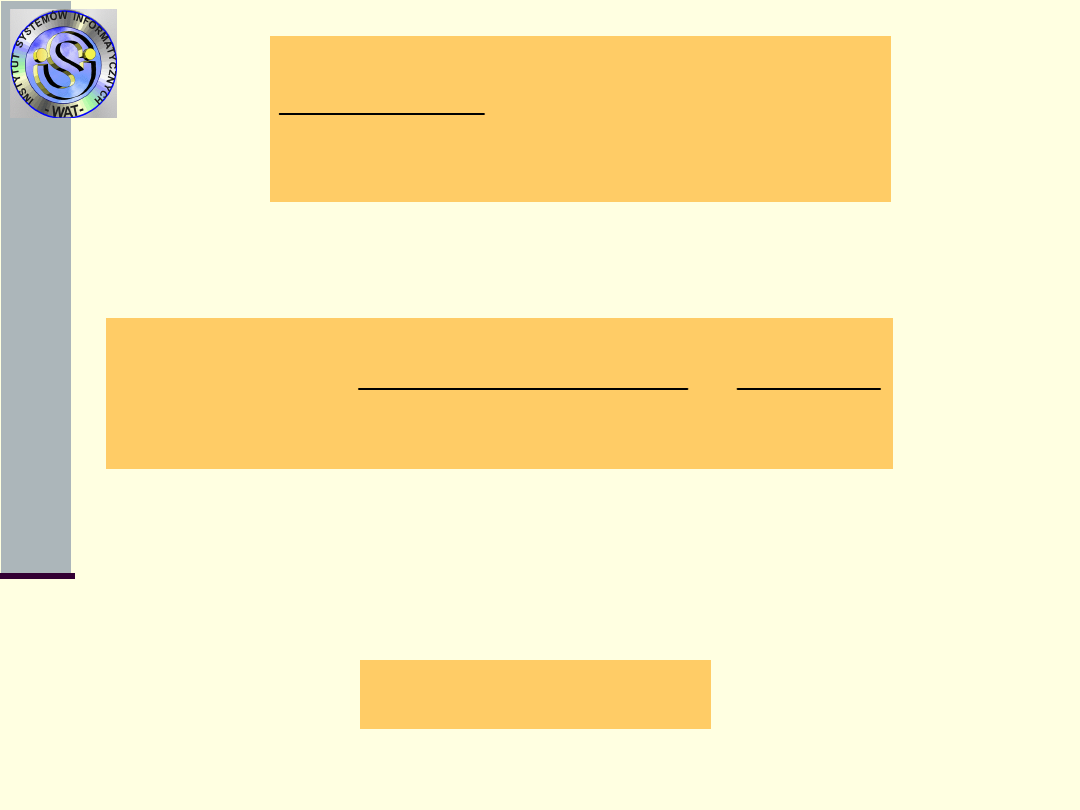
2
,
1
k
,
0
t
)
Z
,
a
(
D
k
czyli ostatecznie
a
C
C
)
t
(
f
)
t
(
F
)
t
(
F
t
t
2
1
k
1
k
k
k
1
k
(5)
Można pokazać, że strategia minimalizującą
K(Z) jest strategia Z(a), przy czym a*
znajduje się z równania
0
*))
a
(
Z
*,
a
(
D
Wynika
stąd
algorytm
służący
do
znajdowania optymalnej strategii kontroli:
• dla zadanego (0<a
C
2
) określić strategię
kontroli
Z(a)
minimalizującą
D(a,D),
wykorzystując algorytm wcześniejszy,
•Zmienić wartość a w taki sposób, żeby
znaleźć a=a*, dla którego D(a*,Z(a*))=0;
wtedy Z(a*) jest strategią optymalną
minimalizującą K(Z).
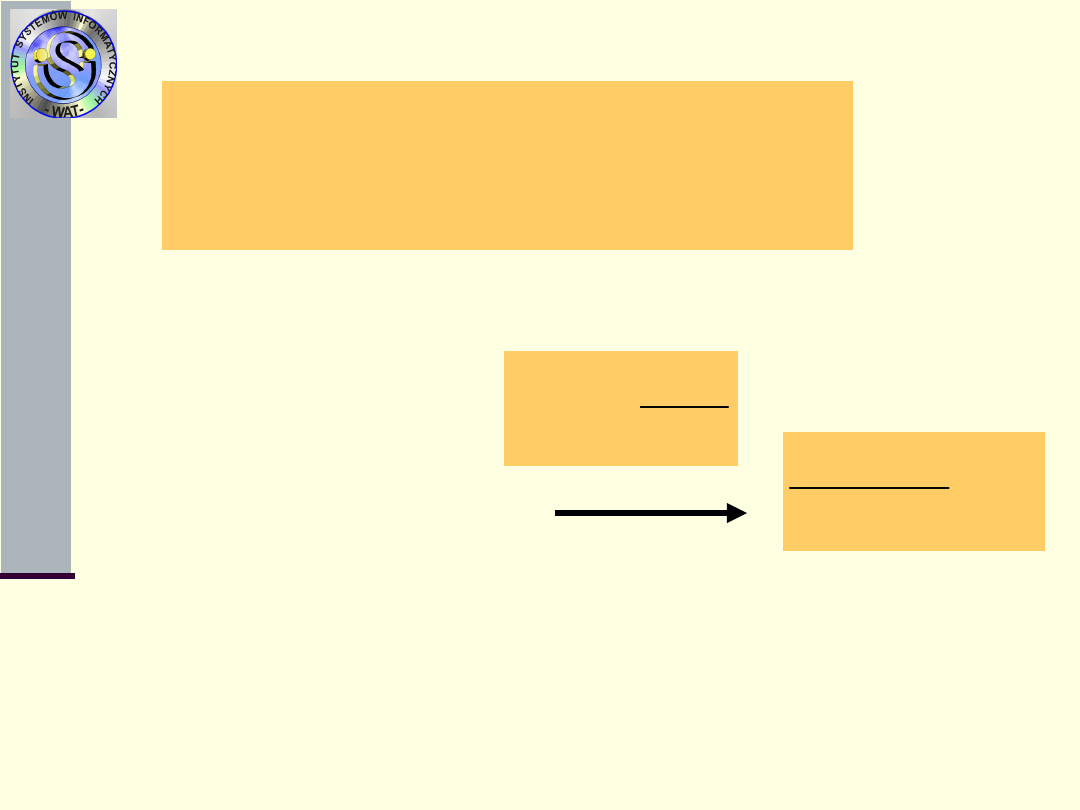
2. Lokalizacja uszkodzeń w systemach
technicznych.
Kontrolę sprawności i lokalizację ewentualnych
uszkodzeń
obiektów
technicznych,
a
w
szczególności
urządzeń
cyfrowych,
można
zrealizować
zasadniczo
dwiema
metodami;
aparaturowa i programową. W pierwszym
przypadku zadanie to wykonuje specjalna
aparatura, a proces kontroli odbywa się w
trakcie normalnej pracy systemu. Kontrola
programowa polega na podawaniu na wejście
systemu (obiektu) specjalnych oddziaływań,
zwanych testami i badaniu reakcji obiektu na te
oddziaływania.
Wymaga
to
najczęściej
przerwania normalnej pracy obiektu i powoduje
określone straty. Powstaje zatem problem
takiego doboru testów i ich kolejności, aby
zamierzony
efekt
został
uzyskany
przy
najmniejszych stratach. Będzie on przedmiotem
dalszych rozważań. Załóżmy, że system złożony
jest z n odpowiednio ze sobą współdziałających
elementów (zbiór G). Każdy element systemu
może znajdować się w jednym z dwóch
możliwych stanów: sprawności lub uszkodzenia.
Prawdopodobieństwo zdarzenia, że i-ty element
znajduje się w stanie sprawności wynosi p
i
, a
prawdopodobieństwo, że element ten znajduje
się w stanie uszkodzenia wynosi q
i
=1- p
i
.
Uszkodzenia
poszczególnych
elementów
są
trwałe i wzajemnie niezależne.
Sprawdzenie sprawności systemu polega na
kolejnym zastosowaniu specjalnych testów, z
których
każdy
sprawdza
ściśle
określony
podzbiór elementów, a koszt (czas) sprawdzenia
testem T
i
wynosi C
i
(t
i
). Cel testowania może być
dwojaki:
• kontrola sprawności całego systemu,
•
lokalizacja
wszystkich
uszkodzonych
elementów.
W pierwszym przypadku wystarczy zastosować
test sprawdzający cały system. Zazwyczaj test
taki jest niemożliwy lub jest niecelowy ze
względu na nieokreśloność uszkodzenia i duże
straty. Zwykle stosuje się kolejno kilka prostych
testów.
Wynik testu T
i
jest dodatni, jeśli w sprawdzonym
przez ten test podzbiorze elementów G
i
nie ma
żadnego uszkodzonego elementu, ujemny, jeśli
wśród sprawdzonych elementów znajduje się co
najmniej jeden uszkodzony.
W ogólnym przypadku podzbiory G
i
sprawdzane
różnymi testami mogą się częściowo pokrywać.
Rozważane
zadania
sprowadzają
się
do
określenia takiej procedury testowania, aby cel
testowania został osiągnięty przy minimalizacji
średnich strat w minimalnym średnim czasie.
Polega to na wyborze ze zbioru testów {T}
niezbędnej grupy testów i określenia kolejności
ich użycia tak, aby proces testowania był
optymalny ze względu na przyjęte kryterium.
Procedura testowania jest na ogół rekurencyjna i
składa się zazwyczaj z dwóch etapów.
Pierwszy
etap
polega na określeniu kolejności testów dla
wyjściowego zbioru elementów G. Ten etap trwa
tak długo, aż wynik kolejnego testu będzie
ujemny albo wszystkie elementy okażą się
sprawne.
Zbiór
wszystkich
elementów
testowanego
systemu można podzielić na trzy następujące
podzbiory:
• G’ – podzbiór elementów, których sprawność
została
stwierdzona za pomocą poprzednich
testów,
• G* - podzbiór elementów sprawdzanych testem,
którego
wynik jest ujemny, z wyjątkiem tych
elementów
tego
podzbioru, których sprawność została
stwierdzona
za
pomocą
poprzednich testów,
• G
0
– podzbiór elementów jeszcze nie
sprawdzonych.
W drugim etapie
podzbiorem wyjściowym jest
zbiór G*. Dla wszystkich testów ze zbiory {T}
następuje
teraz
przewartościowanie
prawdopodobieństw wyniku dodatniego, ze
względu na to, że odnoszą się one teraz do
podzbioru G*.
2.1. Lokalizacja pojedynczego uszkodzenia.
Załóżmy, że system złożony jest z n
elementów. W chwili rozpoczęcia kontroli
wiadomo, że uszkodzony jest dokładnie jeden
element. Należy zlokalizować uszkodzony
element przy minimalnych średnich stratach.
2.1.1. Lokalizacja testami pokrywającymi się.
Przyjmijmy, że do chwili rozpoczęcia M-tego
kroku procedury testowania użyto ciągu
testów s
0
= (T
1
, T
2
,..., T
M-1
). Zadanie sprowadza
się
zatem
do
lokalizacji
uszkodzonego
elementu w podzbiorze G
0
. Na początku
procedury G
0
=G, a s
0
jest zbiorem pustym.
Po
zakończeniu
lokalizacji
wszystkich
niesprawnych elementów w podzbiorze G*
proces
lokalizacji
uszkodzeń
jest
kontynuowany w podzbiorze G
0
.
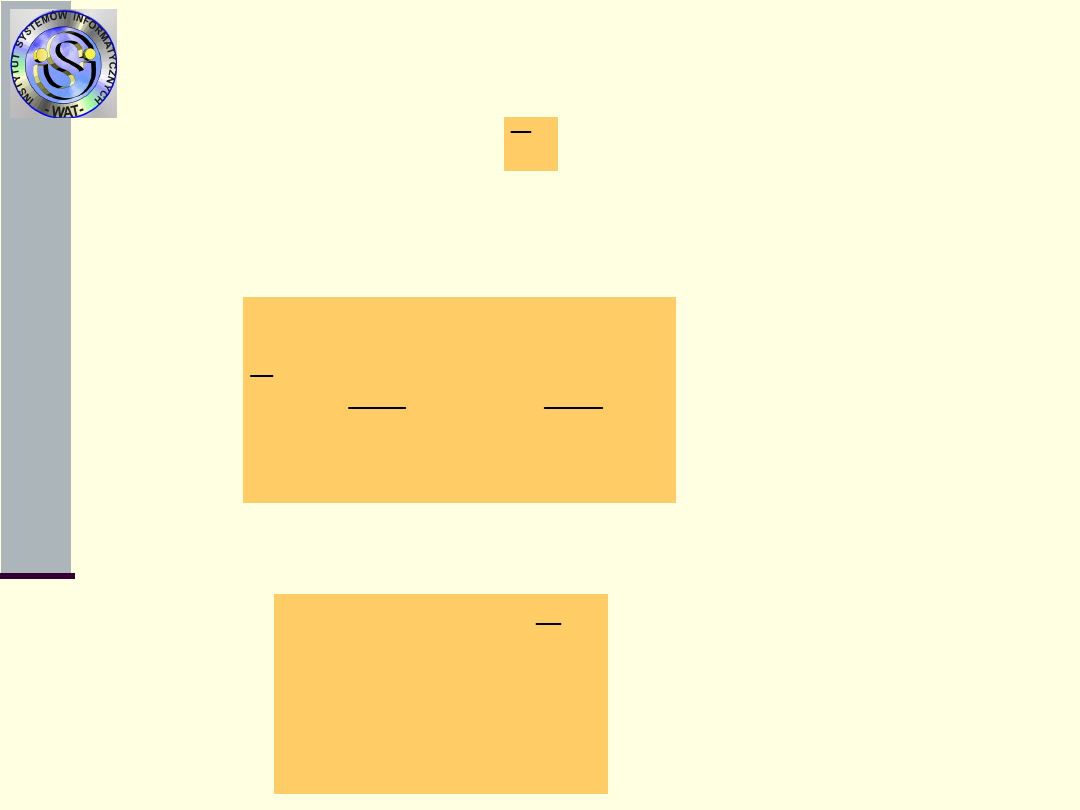
Przybliżony
algorytm
lokalizacji
pojedynczego uszkodzenia elementu jest
następujący:
1.Wyznaczyć wielkości - warunkowe
prawdopodobieństwa, ze uszkodzony jest
dokładnie i-ty element pod warunkiem, że w
sprawdzanym podzbiorze G
0
jest dokładnie
jeden element uszkodzony
2.Dla każdego testu T
j
wyliczyć
prawdopodobieństwo ujemnego wyniku w
sprawdzanym podzbiorze G
0
0
i
q
1
0
G
k
k
k
p
i
0
i
p
q
p
q
q
0
j
G
j
G
i
0
i
0
j
q
Q
3.Dla każdego testu wyliczyć związane z nim
straty
z uwzględnieniem tego, że użyto już ciągu
testów s
0
4.Wybrać taki test T
k
, dla którego g
k
jest
najmniejszy
5.Zastosować test T
k
:
a. Jeśli wynik testu jest dodatni, to zadanie
sprowadza się do lokalizacji uszkodzonego
elementu w podzbiorze
0
j
C
0
j
0
j
j
Q
C
g
j
m
j
i
k
g
g
min
k
0
1
G
\
G
G
- różnica zbiorów
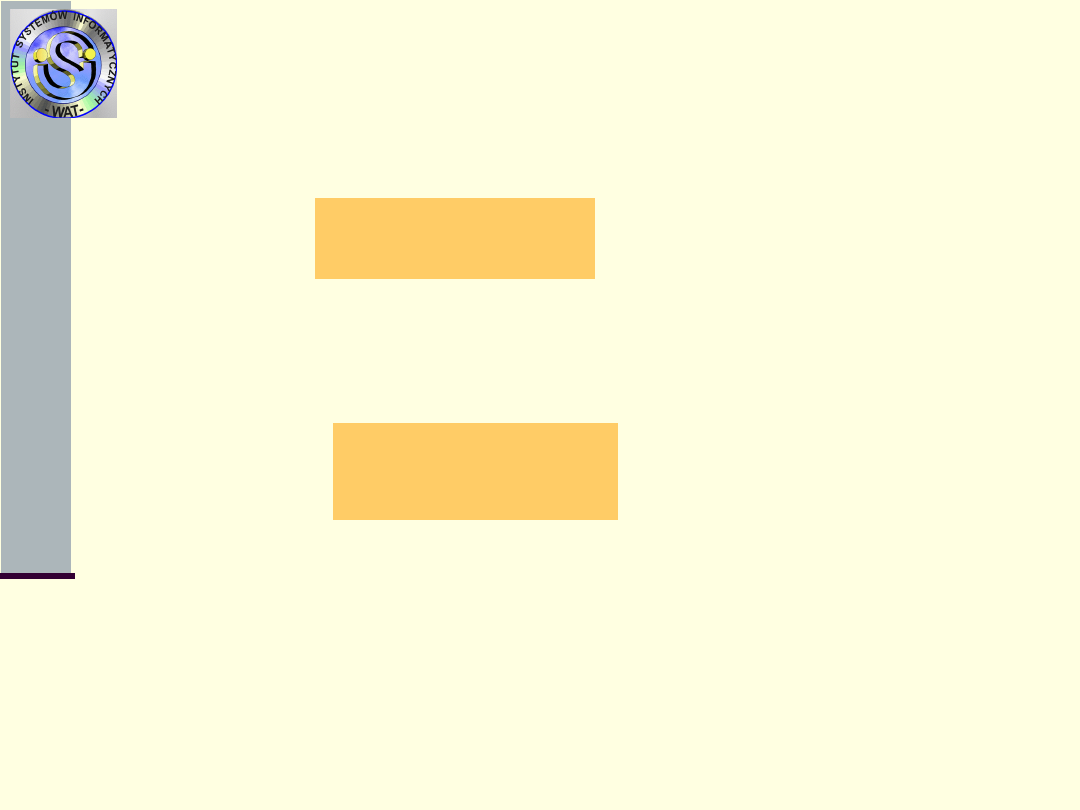
b. Jeśli wynik testu jest ujemny, to zadnie
sprowadza się
do lokalizacji uszkodzonego
elementu w podzbiorze
7. Ustalić ciąg już użytych testów s
1
,
włączając w to poprzedni ciąg s
0
i ostatni
test T
k
8. Do podzbioru G
1
zastosować procedurę
testowania od punktu 1. zmieniając
przedtem główny indeks (0) na indeks (1).
Procedurę testowania kontynuować do
chwili, kiedy w punkcie 6. w pewnym
kroku k powstanie taki zbiór G
k
, który
zawiera tylko jeden element.
0
k
1
G
G
G
k
0
1
T
,
s
s
2.1.2. Testowanie pojedynczych elementów.
Rozpatrzmy przypadek, kiedy test umożliwia
sprawdzenie tylko jednego elementu. Wtedy
optymalna
kolejność
sprawdzania
poszczególnych
elementów
w
celu
lokalizacji uszkodzenia wynika z wartości
wielkości:
i
i
i
i
q
p
c
g
Obliczonych dla każdego elementu. Jako
pierwszy sprawdzeniu podlega element j-ty,
dla którego wartość g
j
jest najmniejsza, a
następnie elementy zgodnie z rosnącymi
wartościami g
k
.
2.1.3. Informacyjna metoda określania
zbioru testów.
Rozpatrzmy metodę testowania, w której
lokalizacja
pojedynczego
uszkodzonego
elementu polega na zastosowaniu takich
testów kontrolnych, z których każdy
umożliwia
podział
zbioru
wszystkich
elementów na dwa podzbiory: w pierwszym
na pewno nie ma uszkodzonego elementu,
w drugim na pewno jest. Zastosowanie
określonego ciągu takich testów umożliwia
dokładna
lokalizacje
uszkodzonego
elementu przy minimum kosztów. Dokładne
rozwiązanie otrzymuje się wówczas, gdy
koszty użycia każdego testu są jednakowe.
Optymalna
lokalizacja
uszkodzonego
elementu
przebiega
zgodnie
z
następującym algorytmem:
1. Dla każdego elementu systemu wyliczyć
warunkowe
prawdopodobieństwa
uszkodzenia
pod
warunkiem,
że
uszkodzony jest dokładnie jeden element
2. Ponumerować elementy tak, aby
3. Dwa ostatnie elementy połączyć w jeden
umowny element, dla którego
4. Tak otrzymany element umieścić w
początkowym
ciągu
elementów
odpowiednio do wielkości
5. Procedurę kontynuować aż do chwili,
kiedy wszystkie elementy będą połączone
w jeden umowny element.
6. Optymalna kolejnością testowania jest
kolejność odwrotna niż kolejność łączenia
elementów.
1
n
1
i
i
i
j
j
j
p
q
p
q
q
1
j
j
q
q
1
n
n
q
q
q
q
2.2. Lokalizacja nieznanej liczby
uszkodzonych elementów.
Testowany
system
jest
złożony
z
n
elementów. Do chwili rozpoczęcia testowania
wiadomo,
że
w
obiekcie
mogą
być
uszkodzone elementy, ale ich liczba nie jest
znana. Po zlokalizowaniu uszkodzonego
elementu wymienia się go na nowy i
przystępuje się do lokalizacji pozostałych
uszkodzonych elementów.
2.2.1. Przybliżony algorytm przy użyciu
pokrywających się testów
Testowany
system
złożony
jest
z
n
elementów. Do chwili testowania wiadomym
jest, że istnieją w nim uszkodzone elementy.
Ich liczba nie jest znana. Po zlokalizowaniu
wymienia się go na nowy i przystępuje się do
lokalizacji
pozostałych
uszkodzonych
elementów tak, aby uzyskać minimalne
średnie straty.
Załóżmy, że do chwili rozpoczęcia M-tego
kroku testowania został użyty ciąg testów s
0
= (T
1
, T
2
,..., T
M-1
). Zadanie sprowadza się
zatem
do
lokalizacji
uszkodzonych
elementów w podzbiorze G
0
. Na początku
procedury G
0
=G, a s
0
jest zbiorem pustym.
1. Stosuje się globalny test dla sprawdzenia,
czy w niekontrolowanym dotąd podzbiorze
G
0
jest chociaż jeden uszkodzony element.
Jeśli wynik jest dodatni, to procedura
testowania jest zakończona. Jeśli ujemny,
to rozpoczyna się podstawowa procedura
opisana poniżej.
2. Jeśli testu globalnego jest ujemny, to dla
każdego testu T
2
wylicza się
prawdopodobieństwo ujemnego wyniku e
testowanym podzbiorze G
0
0
G
i
i
0
G
j
G
i
i
0
j
p
1
p
1
Q
pod warunkiem, że użyto
już ciągu testów s
0
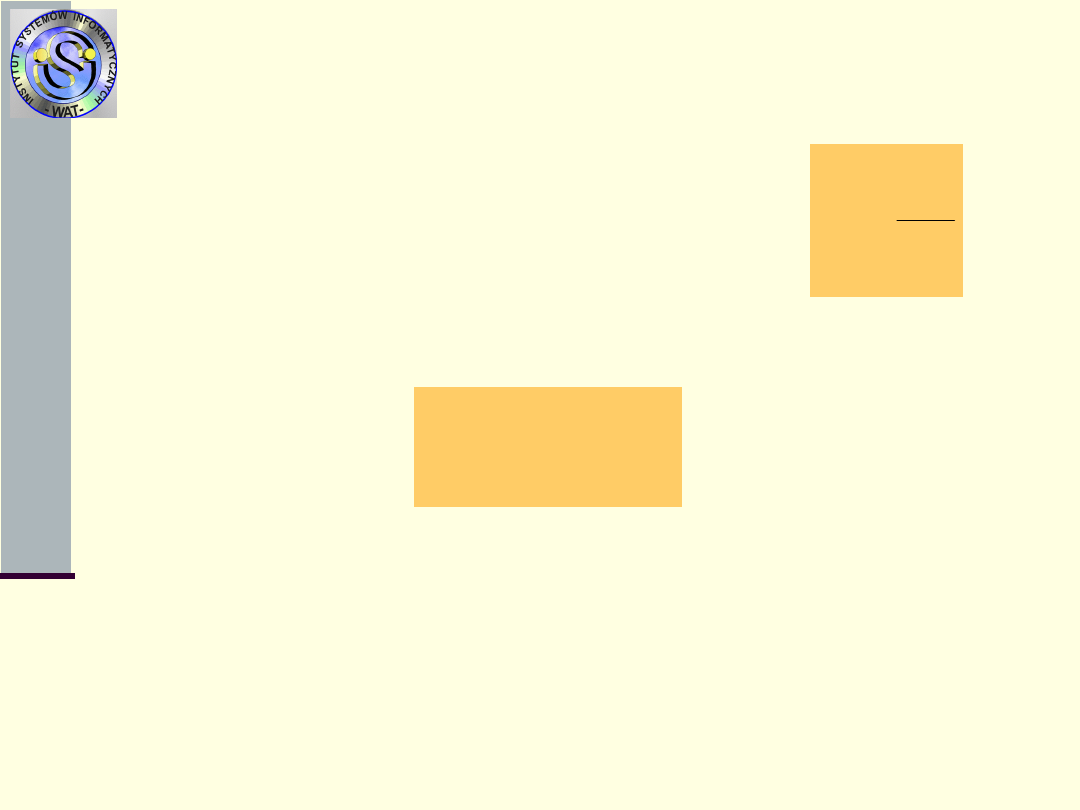
3. Dla każdego testu T
j
wylicza się związane
z nim koszty C
j
0
przy warunku, że użyto
już ciągu testów s
0
(na początku
testowania C
j
0
=C
j
)
4. Dla każdego testu wylicza się wielkość
5. Wybiera się taki test T
k
, dla którego g
k
jest najmniejszy
6. Stosuje się test T
k
, przy czym
a. Jeśli wynik testu T
k
jest dodatni, to
proces lokalizacji uszkodzonych
elementów kontynuuje się dla
pozostałego podzbioru G
1
= G
0
\G
k
0
j
0
j
j
Q
C
g
j
m
j
i
k
g
g
min
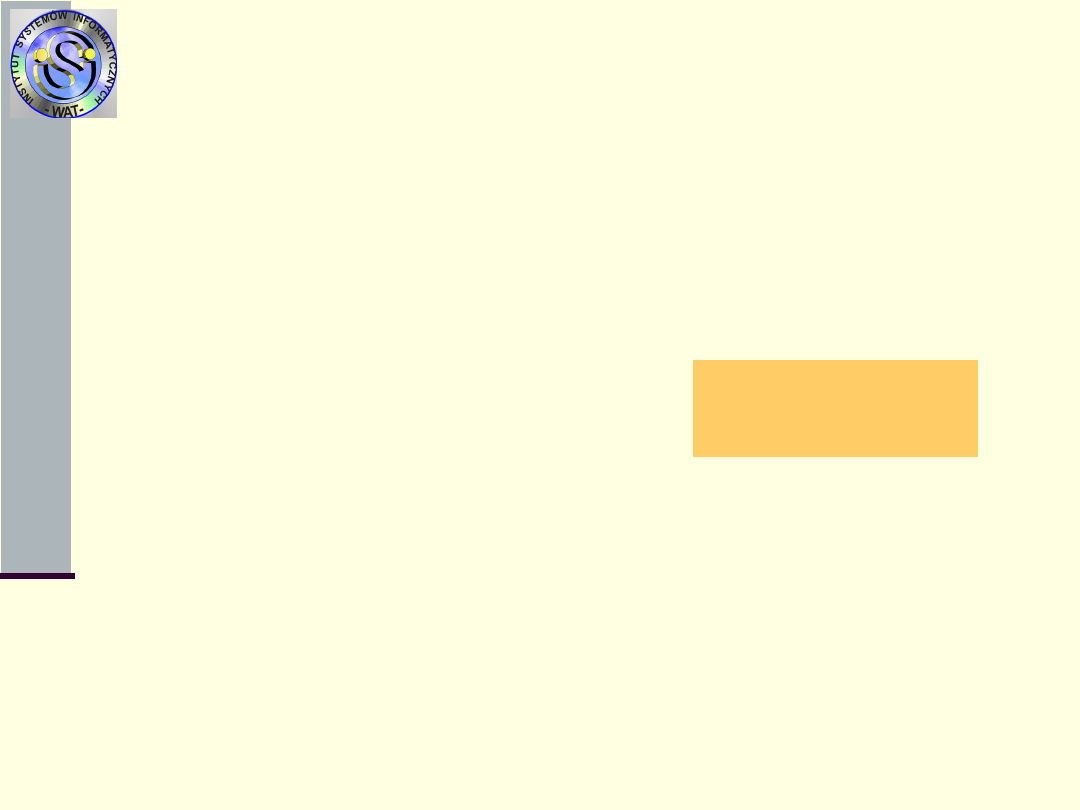
b. Jeśli wynik testu T
k
jest ujemny, to
zadanie składa się z dwu części:
- kolejnej lokalizacji wszystkich
uszkodzonych elementów
w podzbiorze G
1
= G
0
G
k
- lokalizacji uszkodzonych elementów w
pozostałym
podzbiorze G
1
= G
0
\G
k
7. Ustala się nowy ciąg użytych testów s
1
,
włączając w to poprzedni ciąg s
0
i ostatni
test T
k
8. Dla podzbioru G
1
stosuje się nową
procedurę testowania zaczynając od punktu
1., jeśli wynik ostatniego testu był ujemny,
albo zaczynając od punktu 2., jeśli dodatni,
przy czym zmienia się górne indeksy „0” na
indeksy „1”. Proces testowania kontynuuje
się do zlokalizowania wszystkich
uszkodzonych elementów
systemu.
k
0
1
T
,
s
s
2.2.2. Testowanie pojedynczych
elementów.
Załóżmy, że w systemie może być uszkodzonych
kilka elementów. Istnieje możliwość całkowitej
kontroli
sprawności
całego
obiektu
w
określonym
czasie
oraz
testowania
poszczególnych elementów (w czasie
i
dla
każdego elementu). Proces kontroli przebiega w
ten sposób, ze przeprowadza się pełna kontrolę
obiektu
i
jeśli
obiekt
jest
niesprawny,
przystępuje
się
do
testowania
kolejnych
elementów. Testowanie prowadzi się do wykrycia
uszkodzonego elementu. Uszkodzony element
podlega odnowie, po czym sprawdza się
sprawność całego obiektu. Jeśli system w
dalszym ciągu jest niesprawny, to to procedura
jest kontynuowana. Należy znaleźć kolejność
testowania elementów, żeby czas testowania był
minimalny. Można pokazać, że optymalna
kolejność testowania jest wyznaczona według
wzrastających wartości g
i
i
i
i
i
q
p
g
2.2.3. Wykrycie uszkodzonego
elementu.
Testowany system jest złożony z n elementów.
Celem sprawdzenia jest stwierdzenie sprawności
lub niesprawności obiektu, przy czym jeśli jest
on niesprawny, to średni czas stwierdzenia tego
faktu powinien być minimalny (po wykryciu
pierwszego
uszkodzenia
testowanie
jest
przerwane). Zakłada się ,że niemożliwym jest
użycie globalnego testu lub jego użycie związane
jest ze zbyt dużym kosztem.
Algorytm przybliżony (dowolne pokrywające się
testy)
Założenie:
Załóżmy, ze do chwili rozpoczęcia M-tego kroku
procesu testowania został użyty ciąg testów s
0
=
(T
1
, T
2
,..., T
M-1
). Zadanie sprowadza się do
wykrycia co najmniej jednego uszkodzonego
elementu w pozostałym podzbiorze G
0
. Na
początku procedury G
0
=G, a s
0
jest zbiorem
pustym.
1. Dla każdego testu T
j
wyliczyć
prawdopodobieństwo ujemnego wyniku w
sprawdzanym podzbiorze G
0
pod warunkiem, ze użyto już ciągu
testów s
0
2. Dla każdego testu T
j
wyliczyć związane z
nim straty czasu
3. Dla każdego testu T
j
wylicza się wielkość
4. Wybiera się taki test T
j
, dla którego g
k
jest minimalne
0
G
j
G
i
i
0
j
p
1
Q
0
j
0
j
0
j
j
Q
g
j
m
j
i
k
g
g
min
5. Zastosować test T
k
:
a. Jeśli wynik testu T
k
jest dodatni, to proces
wykrywania uszkodzenia kontynuuje się w
podzbiorze
b. Jeśli wynik testu T
k
jest ujemny, to proces
zostaje zakończony, ponieważ podzbiór
elementów G
k
zawiera co najmniej jeden
element uszkodzony.
6. Ustala się nowy ciąg już użytych testów s
1
,
zawierający poprzedni ciąg s
0
i ostatni użyty
test T
k
7. Dla podzbioru G
1
, określonego w punkcie 5,
stosuje się od nowa procedurę testowania od
punktu 1, przy czym indeksy „0” zamienia się
na
indeksy
„1”.
Proces
testowania
kontynuuje się do chwili wykrycia co
najmniej jednego uszkodzenia albo do
całkowitego
sprawdzenia
sprawności
systemu.
(podobna procedura do procedury
lokalizacji nieznanej liczby uszkodzonych
elementów)
k
0
1
G
\
G
G
k
0
1
T
,
s
s
2.2.4. Sprawdzenie systemu
testami rozłącznymi.
Jeśli możliwe jest sprawdzenie systemu tylko
rozłącznymi testami, to znaczy takimi, że
każdy z elementów obiektu może być
sprawdzony
tylko
jednym
testem,
to
optymalna kolejność testowania obiektu w
celu stwierdzenia uszkodzenia wynika z
kolejności wielkości g
i
ponumerowanych
według rosnących wartości
i
i
i
q
g