Seria: Informatyka
Elementy teorii
niezawodności
Wykład 4
Obiekty proste odnawialne
z niezerowym czasem
odnowy
dr hab. inż. Tadeusz Nowicki prof.
nadzw. WAT
e-mail:tadeusz.nowicki@wat.edu.pl, tel.
6-837118
Seria: Informatyka
Elementy teorii
niezawodności
Wykład 4
Obiekty proste odnawialne
z niezerowym czasem
odnowy
dr hab. inż. Tadeusz Nowicki prof.
nadzw. WAT
e-mail:tadeusz.nowicki@wat.edu.pl, tel.
6-837118
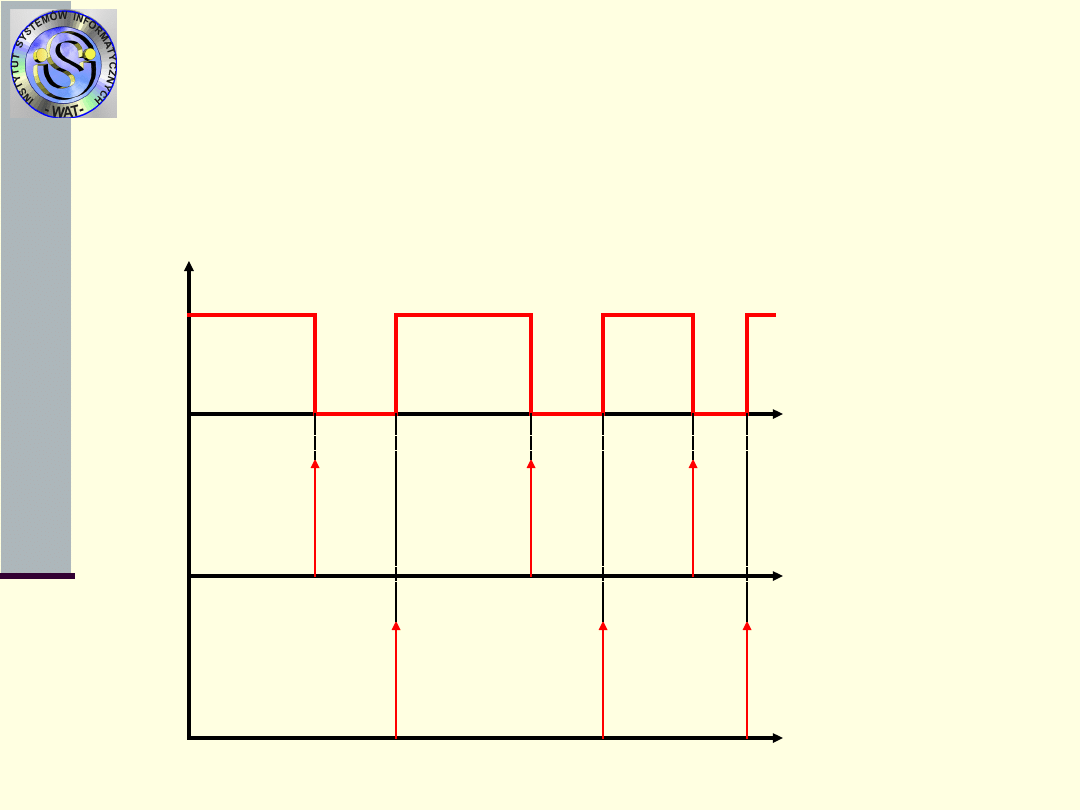
Model niezawodnościowy
Jedynymi istotnymi zdarzeniami w eksploatacji
obiektu prostego odnawialnego z niezerowa
odnową są chwile uszkodzeń i chwile odnowień,
które przy niezerowej odnowie, są chwilami
różnymi.
T
1
t
T
2
T
3
T
4
1
0
1
2
3
N
1
(
t)
N
2
(
t)
strumień
uszkodzeń
strumień
odnowień
X(
t)
Model niezawodnościowy
Naprzemienny ciąg zmiennych losowych:
T
1
,
1
, T
2
,
2
, T
3
,
3
, ...
czasów poprawnej pracy i
czasów
odnów
obiektów
jest
modelem
niezawodnościowym
obiektu
prostego
odnawialnego z niezerowym czasem odnowy.
Zmienne T
i
są zmiennymi losowymi oznaczającymi
kolejne czasy poprawnej pracy obiektu określone
dystrybuantą F(t), gęstością f(t), transformatą
Laplace’a f*(s), wartością oczekiwaną
1
oraz
odchyleniem standardowym
1
.
Zmienne
i
są zmiennymi losowymi oznaczającymi
kolejne
czasy
odnów
obiektu
określone
dystrybuantą G(t), gęstością g(t), transformatą
Laplace’a g*(s), wartością oczekiwaną
2
oraz
odchyleniem standardowym
2
.
Charakterystyki tych zmiennych losowych są
zatem
miarami niezawodnościowymi
obiektu.
Zmienna losowa
Załóżmy, że zmienna losowa
r
jest sumą
zmiennych losowych oznaczających czas poprawnej
r-tej pracy obiektu i czas r-tej odnowy obiektu.
Zmienne losowe
1
,
2
,
3
, ... mają identyczny
rozkład
o dystrybuancie
i gęstości
zatem
r
r
r
T
t
0
r
dx
)
x
(
g
)
x
t
(
F
t
P
)
t
(
t
0
dx
)
x
(
g
)
x
t
(
f
)
t
(
dt
d
)
t
(
)
s
(
g
)
s
(
f
)
s
(
Miary procesu odnowień N
2
(t)
1.
Czas t
”r
do r-tej odnowy– zmienna losowa
spełniająca:
Jej dystrybuanta wyznaczana jest na podstawie
a gęstość
gdzie
r
3
2
1
"
r
...
t
)
s
(
L
)
t
(
r
1
r
)
s
(
r
- transformata
Laplace’a
dystrybuanty
)
s
(
L
)
t
(
r
1
r
)
s
(
r
- transformata
Laplace’a gęstości
)
s
(
g
)
s
(
f
)
s
(
)
s
(
r
r
r
)
s
(
g
)
s
(
f
s
1
)
s
(
s
1
)
s
(
r
r
r
Miary procesu odnowień N
2
(t)
dla czasów odpowiednio dużych (t ) zmienna
losowa t
”r
dąży do rozkładu normalnego
r
,
r
N
2
2
2
1
2
1
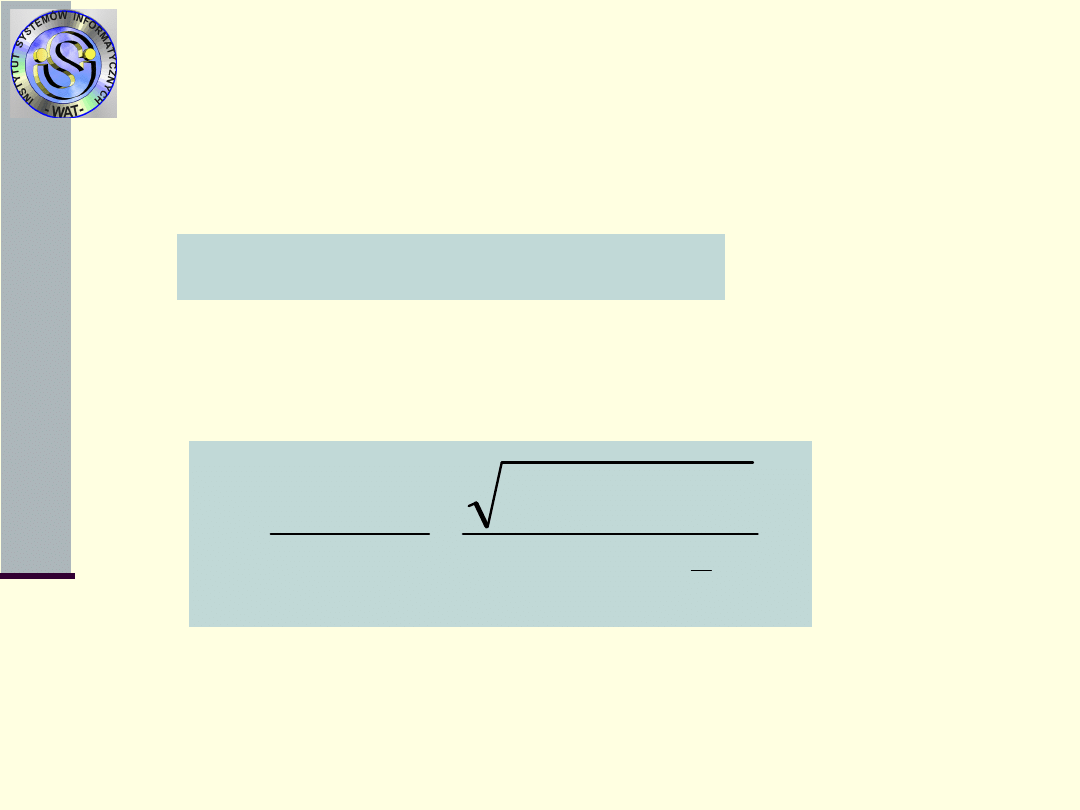
Miary procesu odnowień N
2
(t)
2.
Proces stochastyczny N
2
(t) – liczba odnowień do
chwili
t
Można pokazać, że
Można pokazać, że dla dużych t (odpowiednio
duża liczba odnowień) proces N
2
(t) dąży do
)
t
(
)
t
(
r
t
N
P
1
r
r
2
t
,
t
N
2
3
2
1
2
2
2
1
2
1
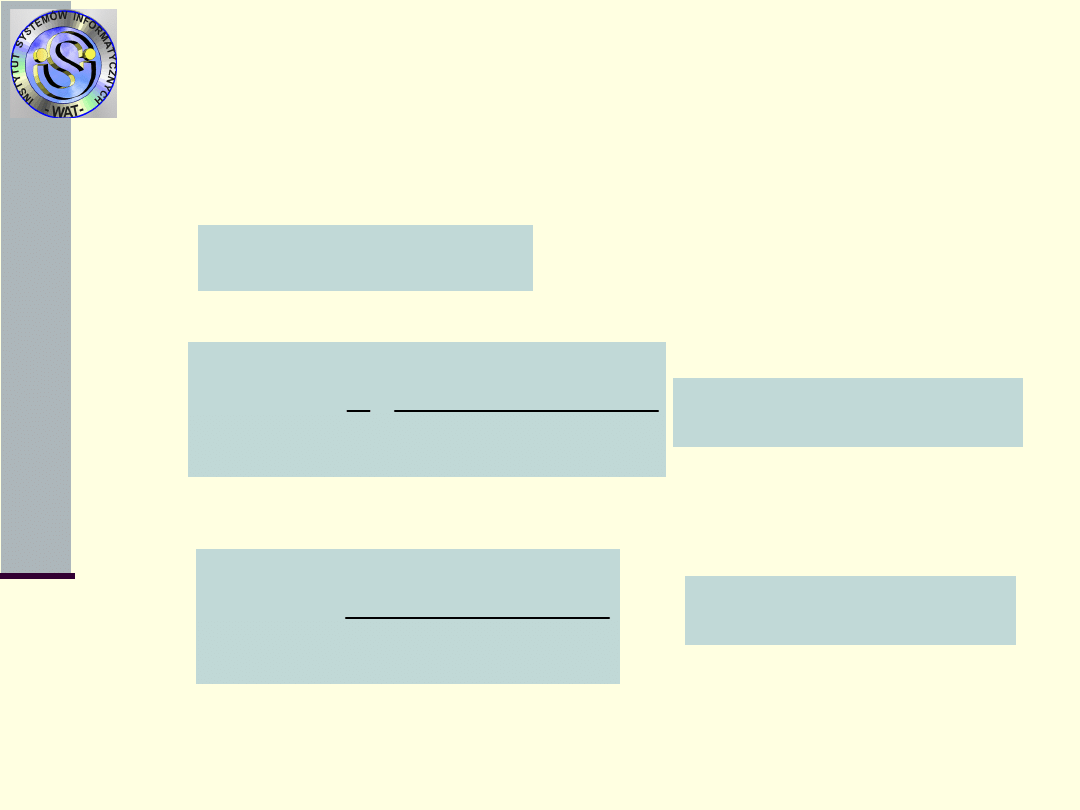
Miary procesu odnowień N
2
(t)
3.
Funkcja odnowy H
2
(t) – oczekiwana
liczba odnowień do chwili t
oraz
4.
Gęstość odnowy h
2
(t)
t
N
E
)
t
(
H
2
2
(s)
g
)
s
(
f
1
(s)
g
(s)
f
s
1
)
s
(
H
2
(s)
g
)
s
(
f
1
(s)
g
(s)
f
)
s
(
h
2
)
s
(
H
L
)
t
(
H
2
1
2
)
s
(
h
L
)
t
(
h
2
1
2
Miary procesu uszkodzeń N
1
(t)
5.
Czas t
’r
do r-tego uszkodzenia– zmienna losowa
spełnia:
Jej dystrybuanta wyznaczana jest na podstawie
a gęstość
gdzie
r
3
2
1
'
r
...
T
t
)
s
(
L
)
t
(
r
1
r
)
s
(
r
- transformata
Laplace’a
dystrybuanty
)
s
(
L
)
t
(
r
1
r
)
s
(
r
- transformata
Laplace’a gęstości
)
s
(
g
)
s
(
f
)
s
(
f
)
s
(
1
r
r
)
s
(
g
)
s
(
f
)
s
(
f
s
1
)
s
(
s
1
)
s
(
1
r
r
r
Miary procesu uszkodzeń N
1
(t)
dla czasów odpowiednio dużych (t ) zmienna
losowa t
’r
dąży do rozkładu normalnego
r
,
r
N
2
2
2
1
2
1
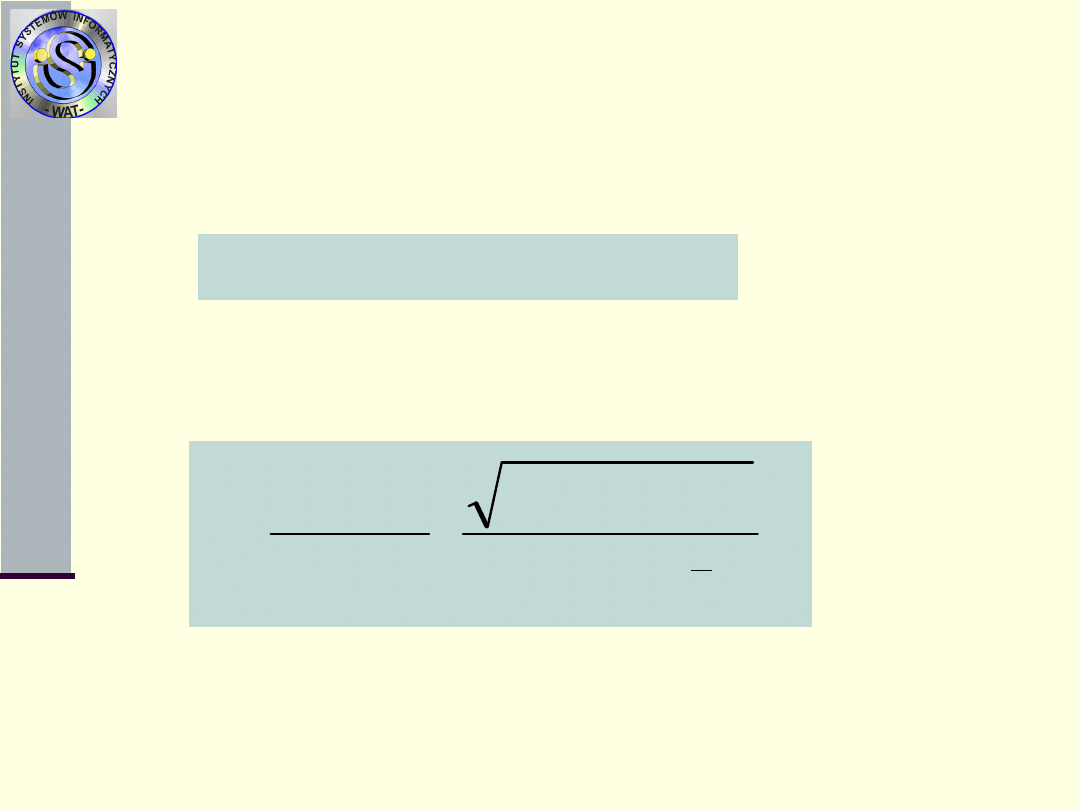
Miary procesu uszkodzeń N
1
(t)
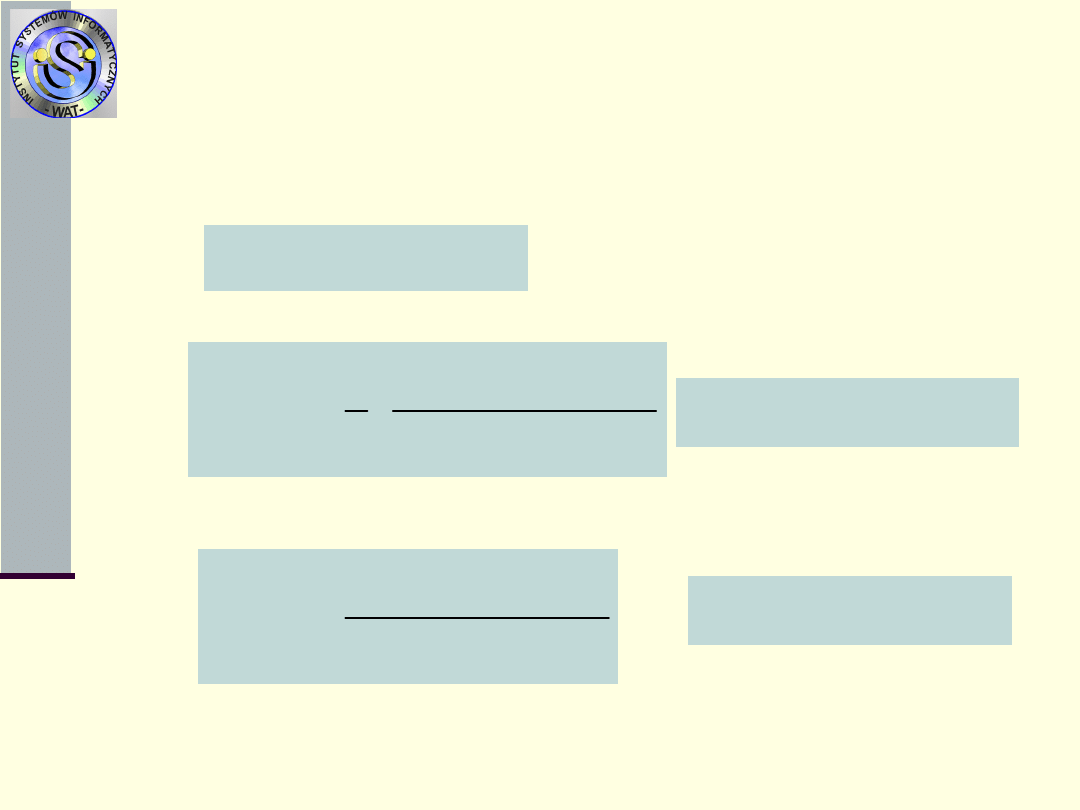
6.
Proces stochastyczny N
1
(t) – liczba uszkodzeń
do
chwili
t
Można pokazać, że
Można pokazać, że dla dużych t (odpowiednio
duża liczba odnowień) proces N
1
(t) dąży do
)
t
(
)
t
(
r
t
N
P
1
r
r
1
t
,
t
N
2
3
2
1
2
2
2
1
2
1
Miary procesu uszkodzeń N
1
(t)
7.
Funkcja odnowy H
1
(t) – oczekiwana
liczba uszkodzeń do chwili t
oraz
8.
Gęstość odnowy h
1
(t)
t
N
E
)
t
(
H
1
1
(s)
g
)
s
(
f
1
(s)
f
s
1
)
s
(
H
1
(s)
g
)
s
(
f
1
(s)
f
)
s
(
h
1
)
s
(
H
L
)
t
(
H
1
1
1
)
s
(
h
L
)
t
(
h
1
1
1
Miary niezawodności łączne dla
strumieni
9.
Współczynnik
gotowości
k
g
(t)
-
prawdopodobieństwo poprawnej pracy obiektu
w chwili t
Można pokazać, że
Stosując przekształcenie Laplace’a
lub
i oczywiście:
1
)
t
(
X
P
)
t
(
k
g
t
0
2
g
du
)
u
t
(
F
1
)
u
(
h
)
t
(
F
1
)
t
(
k
(s)
g
)
s
(
f
1
(s)
f
1
s
1
)
s
(
h
1
)
s
(
f
1
s
1
)
s
(
k
2
g
s
1
)
s
(
H
)
s
(
H
)
s
(
k
1
2
g
)
s
(
k
L
)
t
(
k
g
1
g
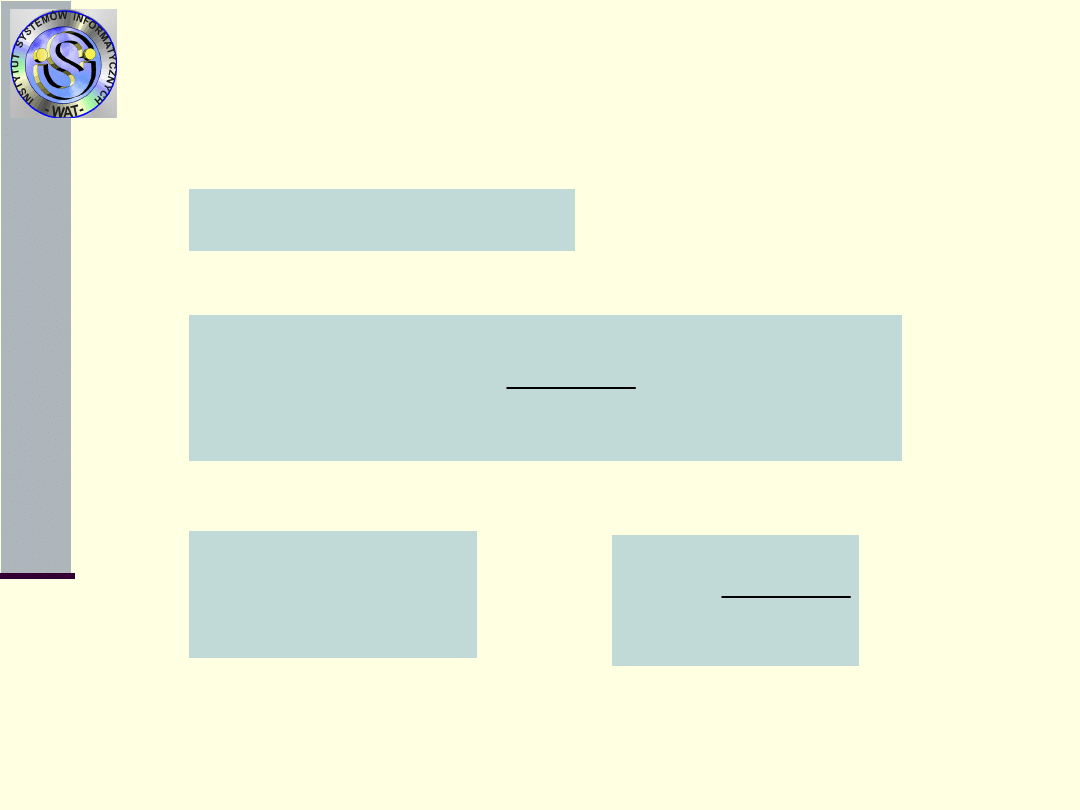
Miary niezawodności łączne dla
strumieni
Zatem
Dla dużych t otrzymujemy:
ale
zatem
0
2
1
g
t
g
du
)
u
(
F
1
1
)
t
(
k
lim
K
1
)
t
(
H
)
t
(
H
)
t
(
k
1
2
g
1
0
du
)
u
(
F
1
2
1
1
g
K
Miary niezawodności łączne dla
strumieni
10.
P(t,t+) – prawdopodobieństwo tego, że w
przedziale (t,t+) nie będzie uszkodzenia
a dla dużych t (korzystając z tw. Smitha)
otrzymujemy charakterystykę graniczną
t
0
2
dx
)
x
t
(
F
1
)
x
(
h
)
t
(
F
1
)
t
,
t
(
P
dy
)
y
(
R
1
)
t
,
t
(
P
lim
)
(
P
2
1
t