
Seria: Informatyka
Metody niezawodności i
eksploatacji
Wykład 9
Modele Markowa w
eksploatacji systemów –
modele klasy DD
dr hab. inż. Tadeusz Nowicki prof.
nadzw. WAT
e-mail:nowicki@isi.wat.edu.pl, tel. 6-
837118

Podstawowe pojęcia i klasyfikacja procesów
stochastycznych
Definicja procesu stochastycznego.
Oznaczenia:
E – zbiór zdarzeń elementarnych (stany procesu
eksploatacji)
T – zbiór wartości parametru t (najczęściej czasu
eksploatacji)
Procesem stochastycznym nazywamy funkcję
X(e,t), eE, t T,
X:ETR, R – zbiór liczb rzeczywistych.
Zauważmy, że dla ustalonego t funkcja X
t
(e) jest
funkcją zdarzenia elementarnego „e”, więc jest
zmienną
losową
(def. zmiennej losowej: X :ER)
Dla ustalonego e funkcja X
t
(t) jest funkcją
rzeczywistą (bo „e” się zrealizowało).

(X,T,F)
Gdzie X –zbiór stanów eksploatacyjnych
systemu, T – zbiór wartości parametru, F –
rodzina dystrybuant
F(x
1
, x
2
,..., x
n
, t
1
, t
2
,..., t
n
)= P(X(t
1
)< x
1
,..., X(t
i
)<
x
i
,..., X(t
n
)< x
n
)
Dla dowolnych n=1,2,... Oraz dowolnego
naboru wartości t
i
.
Dla uniknięcia błędów przyjmijmy oznaczenia:
X(t) – proces stochastyczny, x(t) – realizacja
procesu stochastycznego, Y – zmienna losowa, y
– realizacja zmiennej losowej.
Proces stochastyczny będziemy oznaczali
symbolem X(t). Proces będzie określony
probabilistycznie, gdy określona będzie
trójka:
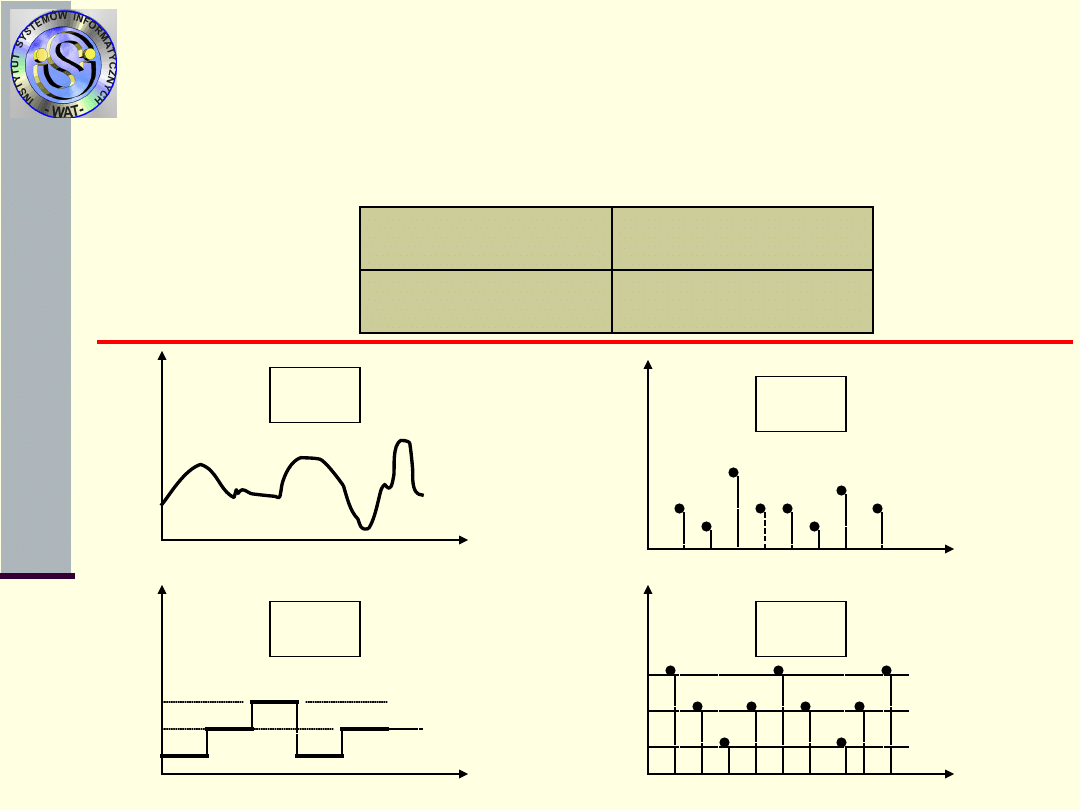
Podział procesów stochastycznych na klasy
Ze względu na rodzaje zbiorów X i T (ciągłe i
dyskretne)
CC
DC
DD
CD
X
ciągł
y
dyskret
ny
T
ciągł
y
dyskret
ny
x(t)
t
CC
x(t)
t
CD
1 2 3 4 5 6 7 8
x(t)
t
DD
1
2
3
1 2 3 4 5 6 7 8 9
x(t)
t
DC
1
2
3

Procesy Markowa
Niech {t
i
: i=1,..,n} będzie dowolnym ciągiem
rosnącym wartości parametru tT dla
dowolnego n. Proces jest procesem Markowa
wtedy i tylko wtedy, gdy
P(X(t
n
)<x
n
X(t
n-1
)=x
n-1
, X(t
n-2
)=x
n-2
,...,
X(t
0
)=x
0
)=
= P(X(t
n
)< x
n
X(t
n-1
)=x
n-1
)
Proces Markowa nazywamy ahistorycznym, bo
dla pełnej charakterystyki stochastycznej
procesu w chwili t
n
jest wystarczająca
znajomość tego procesu w dowolnej chwili t
n-1
oraz
zbioru
dystrybuant
warunkowych
rozkładów
jednowymiarowych
określonych
prawą stroną powyższej nierówności.
Twierdzenie.
Jeżeli
proces
X(t)
jest
procesem
o
niezależnych przyrostach, to jest on procesem
Markowa.

Procesy Markowa klasy DD (łańcuchy
Markowa)
Definicja procesu Markowa klasy DD.
Łańcuchem Markowa nazywamy proces
stochastyczny Markowa klasy DD
Oznaczmy proces przez X(t)
Niech X={1,2,...,n}
T={t
0
,t
1
,...} X(t
k
)=i X(k)=i
Opis probabilistyczny
Chwilowe rozkłady bezwarunkowe P
i
(k)=P{X
(k)=i}, i=1,2,...,n, k=0,1,...
Macierz stochastyczna : macierze
prawdopodobieństw przejść
k
l
,...,
2
,
1
k
,l
,
)
k
,
l
(
p
)
k
,l
(
*
n
n
ij
Jednorodne łańcuchy Markowa
Zgodnie z definicją jednorodności
k
l
),
l
k
(
)
k
,
l
(
*
)
k
,
l
(
*
n
n
ij
)
l
k
(
p
)
l
k
(
przyjmując
l=0
,...
2
,
1
k
,
)
k
(
p
)
k
(
n
n
ij
)
k
(
p
ij
warunkowe prawdopodobieństwo
przejścia po k krokach
}
i
)
t
(
X
/
j
)
k
t
(
X
{
P
)
k
(
p
ij

Opis probabilistyczny jednorodnego
łańcucha Markowa
Chwilowe rozkłady prawdopodobieństwa
(bezwarunkowe)
,...
2
,
1
,
0
k
,
n
,...,
2
,
1
i
},
i
)
k
(
X
{
P
)
k
(
p
i
dla ustalonej wartości t-l=k jedna macierz
prawdopodobieństw przejść
n
n
ij
)
k
(
p
)
k
(
Okaże się, że
wystarczy:
Rozkład
początkowy
Jedna macierz
n
,...,
2
,
1
i
},
i
)
0
(
X
{
P
)
0
(
p
i
n
n
ij
)
1
(
p
)
1
(
Własności macierzy (k), k=0,1,2,...
i jej elementów
1
)
k
(
p
0
ij
n
1
j
ij
1
)
k
(
p
i
macierz
stochastyczna
Rozkład chwilowy jako wektor P(t)
}
i
)
t
(
X
{
P
)
t
(
P
))
t
(
P
),...,
t
(
P
),
t
(
P
(
)
t
(
P
i
n
2
1
1
)
t
(
p
0
i
,...
2
,
1
,
0
t
,
1
)
t
(
p
n
1
i
i
warunek
rozkład
u
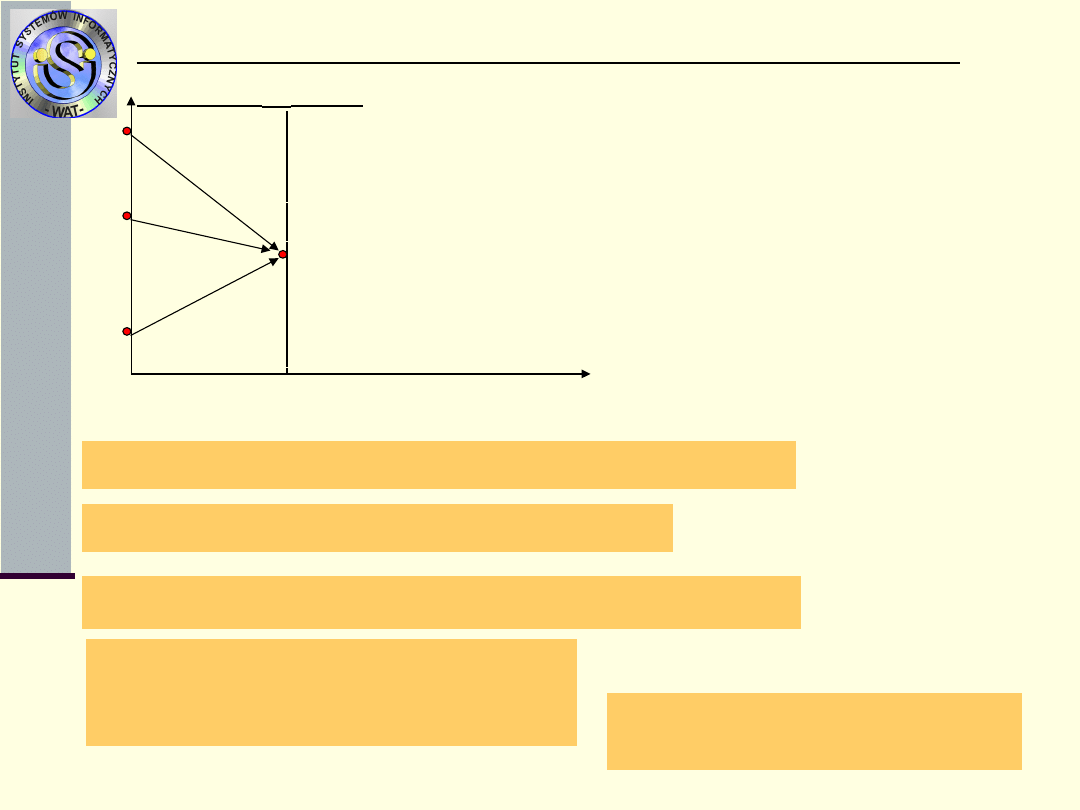
Wyznaczenie rozkładu P(1) na podstawie
P(0) i (1)
1
2
1
r
n
X(t)
j
t
Zastosujmy wzór
na
prawdopodobieńst
wo całkowite
}
1
)
0
(
X
/
j
)
1
(
X
{
P
}
1
)
0
(
X
{
P
}
j
)
1
(
X
{
P
}
n
)
0
(
X
/
j
)
1
(
X
{
P
}
n
)
0
(
X
{
P
...
zatem
)
1
(
p
)
0
(
P
...
)
1
(
p
)
0
(
P
)
1
(
p
)
0
(
P
}
j
)
1
(
X
{
P
nj
n
j
2
2
j
1
1
n
,...,
2
,
1
j
),
1
(
p
)
0
(
P
)
1
(
P
rj
r
n
1
r
j
ogólnie
)
1
(
)
0
(
P
)
1
(
P
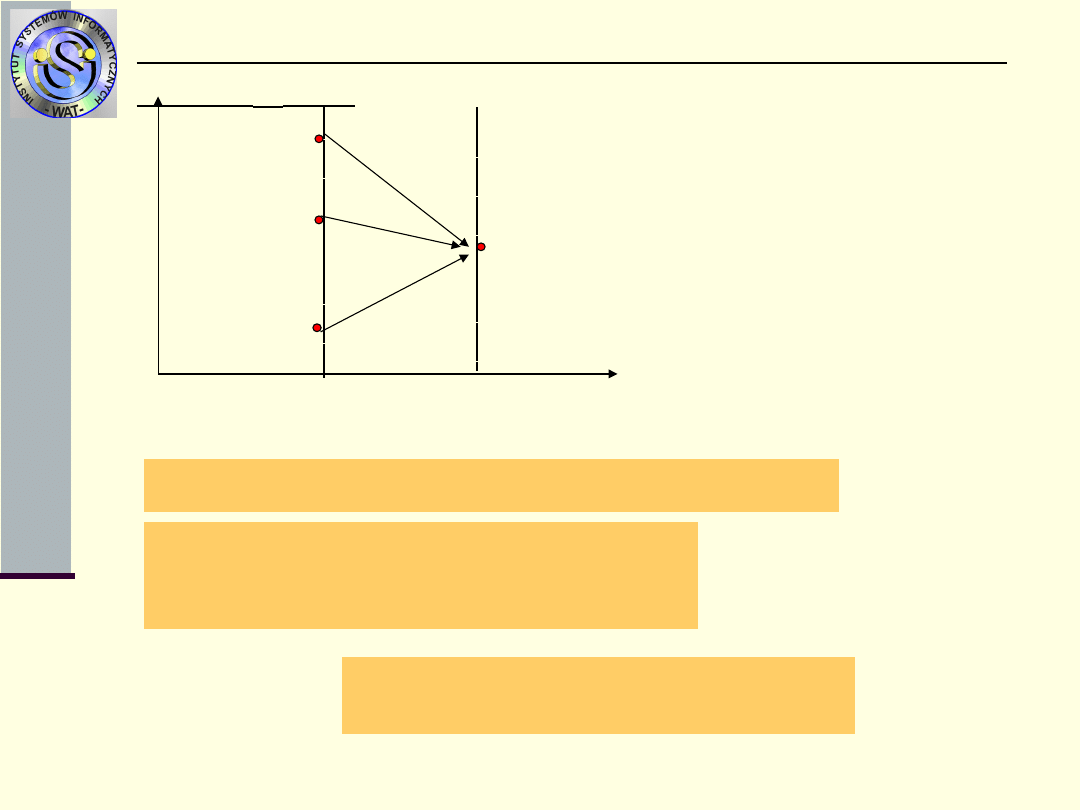
Wyznaczenie rozkładu P(t+k) na podstawie
P(t) i (k)
)
k
(
p
)
t
(
P
...
)
k
(
p
)
t
(
P
)
k
(
p
)
t
(
P
)
k
t
(
P
nj
n
j
2
2
j
1
1
j
n
,...,
2
,
1
j
),
k
(
p
)
t
(
P
)
k
t
(
P
rj
r
n
1
r
j
ogólnie
)
k
(
)
t
(
P
)
k
t
(
P
Analogicznie jak
poprzednio
X(t)
t
t+
k
1
r
n
j
t
Wyznaczenie (k) na podstawie (1)
Tw. Dla jednorodnego łańcucha Markowa
)
1
(
)
k
(
k
Wniosek:
1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1
I
)
1
(
)
0
(
0
Dla uproszczenia oznaczmy
)
1
(
Wniosek:
Jednorodny łańcuch Markowa jest całkowicie opisany
probabilistycznie przez zadanie
• rozkładu początkowego P(0)
• macierzy prawdopodobieństw przejść
gdzie p
ij
jest warunkowym prawdopodobieństwem
przejścia w jednym kroku
n
n
ij
p
Wniosek: równania Chapmana-Kołmogorowa
(dla łańcuchów)
Zauważmy, że
)
s
(
)
k
(
)
s
k
(
stąd
n
,...,
2
,
1
j
,
i
),
s
(
p
)
k
(
p
)
s
k
(
p
rj
ir
n
1
r
ij
Układ tych równań nosi nazwę równań
Chapmana-Kołmogorowa
(Klasyfikacja stanów)
Twierdzenie Markowa
Jeśli łańcuch Markowa jest łańcuchem
ergodycznym, tzn. wszystkie stany łańcucha
są ergodyczne, to istnieją granice
j
ij
k
p
)
k
(
p
lim
Wniose
k:
n
2
1
n
2
1
n
2
1
n
2
1
k
k
k
p
p
p
p
p
p
p
p
p
p
p
p
)
k
(
lim
lim
Twierdzenie (ergodyczne)
Jeśli istnieje takie k>0, że wszystkie elementy
p
ij
(k) macierzy są dodatnie, to łańcuch
Markowa jest ergodyczny i istnieją granice
j
ij
n
p
)
n
(
p
lim
Twierdzenie
Jeżeli łańcuch Markowa jest ergodyczny, to
wielomian charakterystyczny macierzy
)
I
det(
)
(
w
Ma dokładnie jeden pierwiastek
1
=1 , a
wszystkie pozostałe pierwiastki są co do modułu
mniejsze od jedności
,...
3
,
2
i
,
1
i
Twierdzenie (ergodyczne słabsze)
Jeśli istnieje takie k, od którego spełnione
są warunki
n
r
,
j
,...,
j
,
j
j
,
n
,...
2
,
1
i
,
0
)
k
(
p
r
2
1
ij
to istnieją
granice
j
innych
dla
0
j
,...,
j
,
j
j
dla
0
p
)
n
(
p
r
2
1
j
ij
n
lim
Obliczenie rozkładu granicznego
1.
1
k
k
1
k
k
k
k
lim
lim
0
)
-
(I
0
P
)
p
(
n
1
j
j
ij
ij
2.
0
)
I
(
0
)
p
(
P
n
1
j
ij
ij
j
3.
0
)
I
(
P
P
P
0
)
I
(
P
)
k
(
P
P
lim
k
- rozkład graniczny -
wektor
]
p
,...,
p
,
p
[
p
p
p
p
p
p
p
p
p
]
p
,...,
p
,
p
[
n
2
1
nn
2
n
1
n
n
2
22
21
n
1
12
11
n
2
1
n
,...,
2
,
1
j
,
P
p
P
n
1
i
j
ij
i
w każdym
przypadku układ
n równań
jednorodnych
Weźmy pod uwagę układ równań
0
)
I
(
P
]
P
,...,
P
,
P
[
P
n
2
1
wektor niewiadomych
znormalizujmy ten układ do
postaci
0
0
0
P
P
P
1
p
p
p
p
1
p
p
p
p
1
p
n
2
1
nn
n
2
n
1
2
n
22
12
1
n
21
11
Aby
istniało
rozwiązanie
niezerowe
zamieniamy jedno z tych równań (na przykład
ostatnie) oczywistym równaniem postaci
1
P
...
P
P
n
2
1

Wtedy
1
0
0
P
P
P
1
1
1
p
1
p
p
p
p
1
p
n
2
1
2
n
22
12
1
n
21
11
Stosując
wzory
Cramera
otrzymujemy
jednoznaczne
rozwiązanie
tego
układu
równań liniowych, gdy wyznacznik macierzy
współczynników tego układu jest równy zeru.
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
Wyszukiwarka
Podobne podstrony:
wyklad 3 MNE
wyklad 8 MNE
wyklad 4 MNE
wyklad 7 MNE
wyklad 2 MNE
wyklad 2 MNE
wyklad 3 MNE
wyklad 6 MNE
wyklad 5 MNE
więcej podobnych podstron