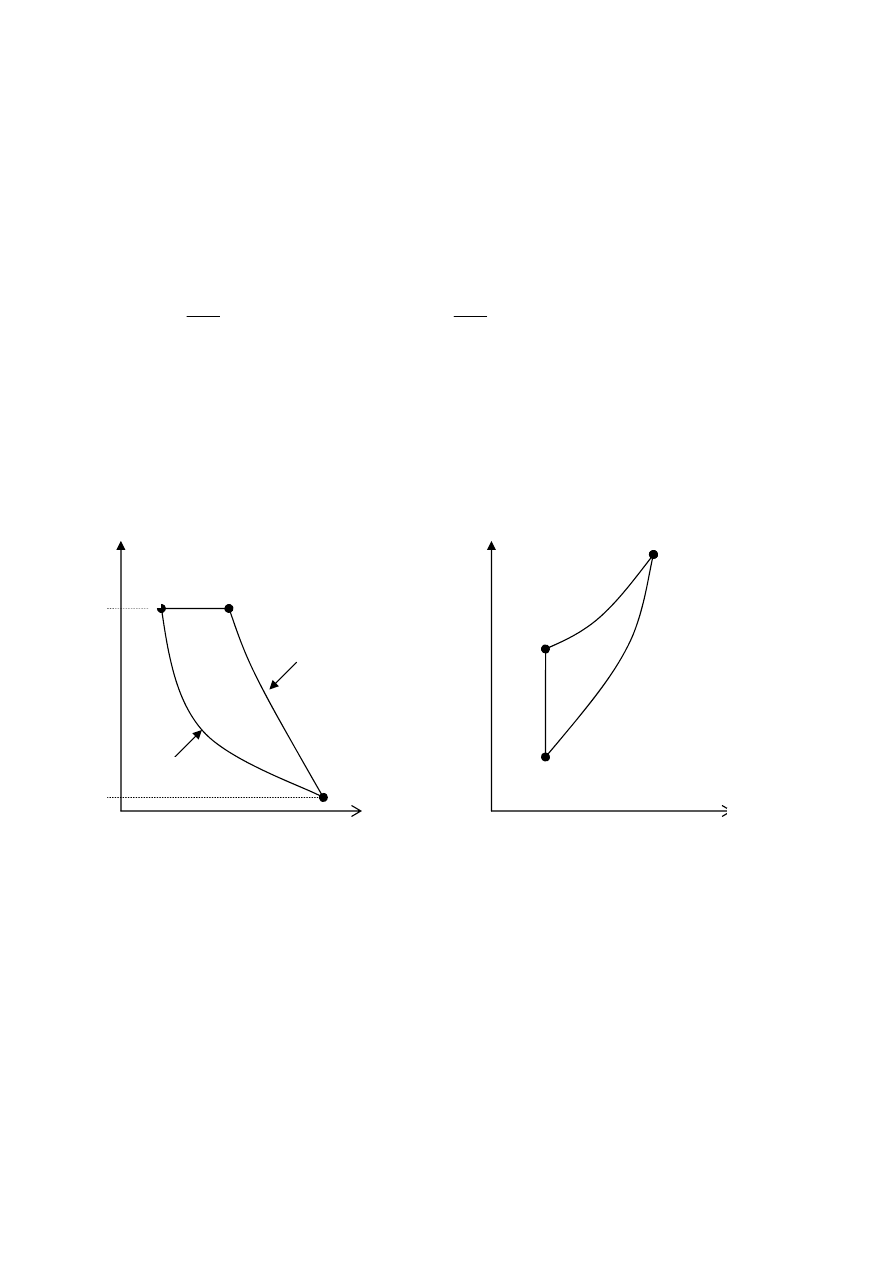
p

2

=p

3

Zadanie II 3.1

Obieg prawobieżny złożony jest z odwracalnych przemiana termodynamicznych, adiabaty

zgęszczania, izobary i politropy. Czynnikiem roboczym jest azot traktowany tak jak gaz

doskonały. Ciśnienie i temperatura na początku przemiany adiabatycznej zgęszczania azotu

jest równa p

1

= 0,9[at] i t

1

=27[

o

C] zaś na jej końcu T

2

=900[K], natomiast temperatura

początku przemiany politropowej T

3

=1900[K]. Indywidualna stała gazowa azotu

R=296,75[

kgK

J

] zaś ciepło właściwe C

p

=1043[

kgK

J

]. Obliczyć parametry stanu w punktach

charakterystycznych obiegu oraz wykładnik politropy.

Rozwiązanie

1. Wykresy prawobieżnego obiegu termodynamicznego azotu we współrzędnych p,

υ oraz T, s

1

2

1

2

3

c= const

s= const

3

p

1

υ

p

s

T

2. Tabela zestawienia danych oraz wyników obliczeń

punkt charaktery-

styczny

parametr stanu

1 2 3

p

i

[p

1

]

1

1

2

2

p

T

T

p

R

Cp

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

p

3

=p

2

T

i

[T

1

] [T

2

] [T

3

]

υ

1

1

p

RT

=

υ

1

2

2

1

2

p

R

T

T

T

R

Cp

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

υ

1

3

2

1

3

p

R

T

T

T

R

Cp

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

υ

3.Obliczam parametry stanu w punktach charakterystycznych obiegu

3.1 Obliczam masową gęstość zasobu objętości w punkcie 1

1

1

p

RT

=

υ

3.2 Obliczam gęstość zasobu objętości powietrza w punkcie 2

Z równania mamy:

const

p

k

=

υ

,

piszemy równanie na z punktu 1 i 2 i otrzymujemy zależności:

k

k

p

p

2

2

1

1

υ

υ

=

υ

RT

p

=

1

2

2

1

1

1

−

−

=

k

k

T

T

υ

υ

stąd

1

1

2

1

2

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

k

T

T

υ

1

1

2

1

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

k

T

T

υ

1

2

1

2

1

1

1

p

R

T

T

T

p

R

T

k

k

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

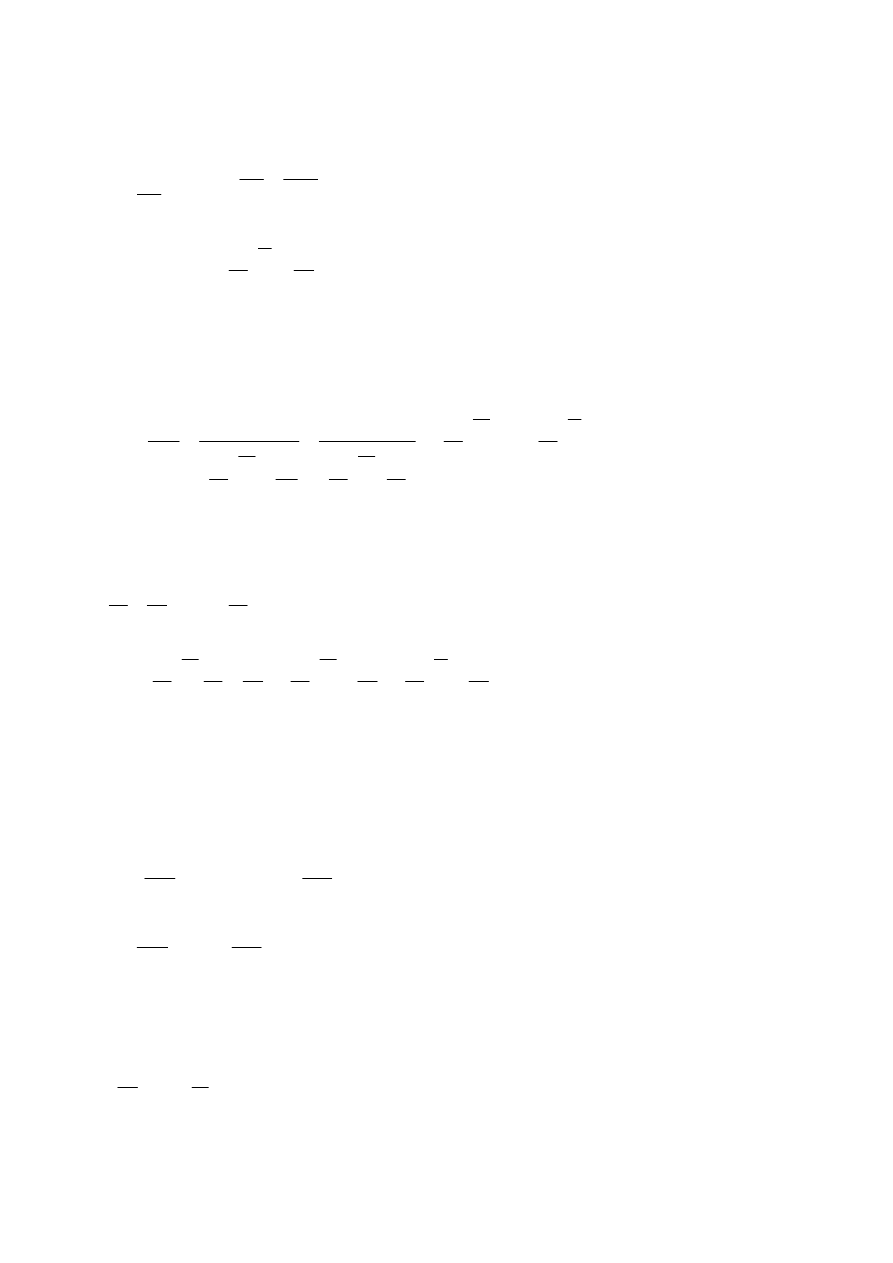
Z równania Mayer’a oraz z definicji izotropii określamy zależności

υ

υ

C

C

k

R

C

C

p

p

=

=

−

⇒

1

−

=

k

k

R

C

p

otatecznie:

1

2

2

1

p

R

T

T

T

R

Cp

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

υ

4. Obliczam ciśnienie powietrza w punkcie 2 obiegu

Z równania stanu gazu doskonałego mamy:

1

1

2

1

1

1

2

2

1

1

1

2

1

1

2

1

1

1

2

1

2

2

2

p

T

T

p

T

T

T

T

T

T

p

p

R

T

T

T

RT

RT

p

R

Cp

k

k

k

k

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

=

−

−

−

υ

5. Obliczam masową gęstość zasobu objętości powietrza w punkcie 3 obiegu. Między

punktami 2 a 3 mamy przemianę izobaryczną.

2

2

3

3

2

3

2

υ

υ

υ

υ

T

T

T

T

s

=

⇒

=

1

3

2

1

1

3

1

2

1

1

3

2

1

1

1

2

1

3

p

R

T

T

T

p

R

T

T

T

p

R

T

T

T

T

T

R

Cp

k

k

k

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

−

−

υ

6. Obliczam wykładnik politropy z równania politropy

n

n

p

p

1

1

3

3

υ

υ

=

Z równania stanu gazu doskonałego Clapeyron’a

3

3

3

p

RT

=

υ

1

1

1

p

RT

=

υ

n

n

p

RT

p

p

RT

p

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

1

1

1

3

3

3

stąd:

n

n

n

n

T

p

T

p

3

1
3

1

1

1

−

−

=

n

n

T

T

p

p

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

1

3

1

3

1

(

)

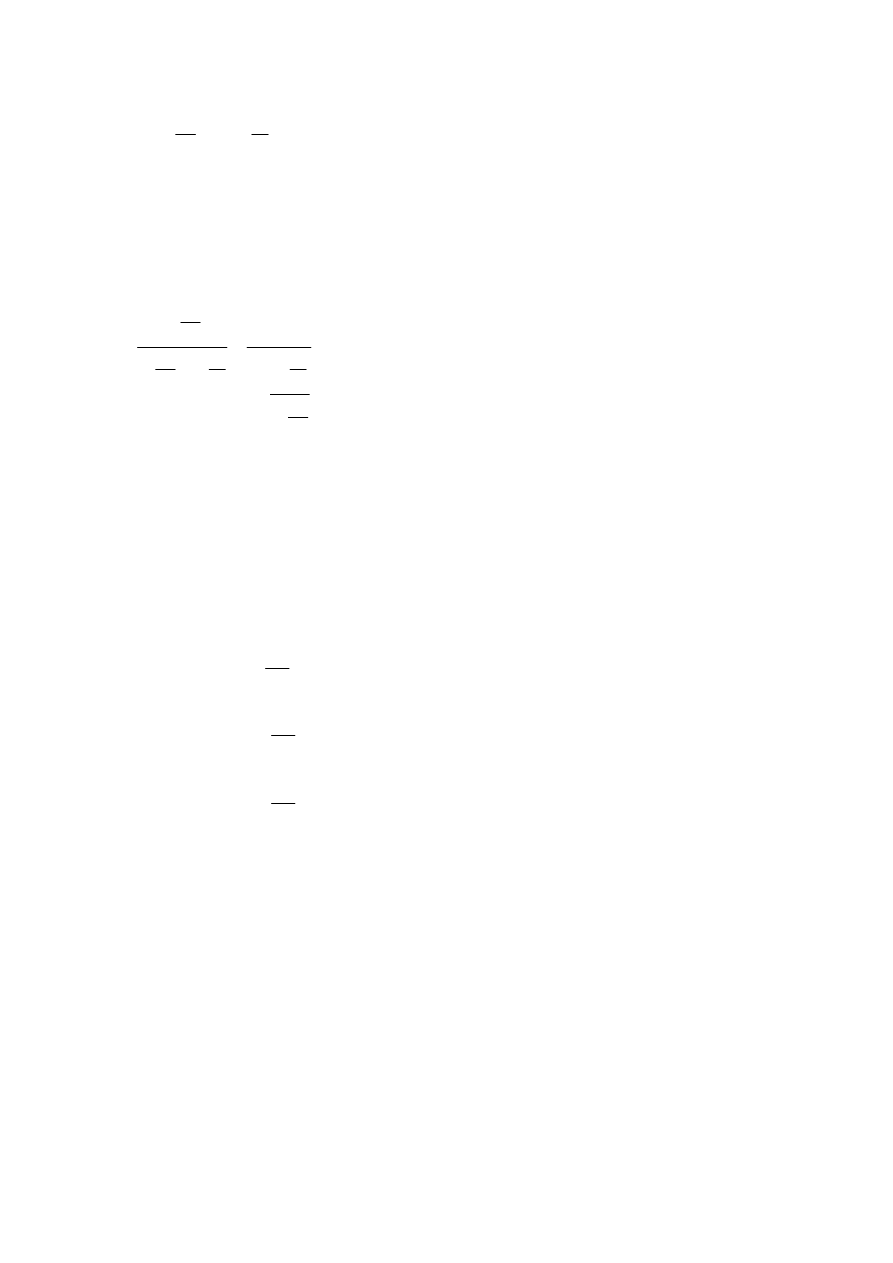
1

3

3

1

ln

ln

1

T

T

n

p

p

n

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

ostatecznie:

3

1

1

3

1

3

3

1

3

1

ln

ln

1

1

ln

ln

ln

p

p

T

T

T

T

p

p

p

p

n

+

=

+

=

6. Obliczam wartości parametrów stanu w punktach charakterystycznych obiegu

6.1 Obliczam wartości parametrów stanu w punktach charakterystycznych obiegu

p

2

= 4,188848[MPa]

p

3

=p

2

= 4,188848[MPa]

p

1

= 0,9 · 9,81 · 10

4

= 0,08829 [MPa]

7. Obliczam wartości mas gęstości zasobu azotu w punktach charakterystycznych obiegu

υ

1

= 1,00886

⎥

⎦

⎤

⎢

⎣

⎡

kg

m

3

υ

2

= 0,063764

⎥

⎦

⎤

⎢

⎣

⎡

kg

m

3

υ

3

= 0,134613

⎥

⎦

⎤

⎢

⎣

⎡

kg

m

3

8. Obliczam wartość wykładnika politropie

n = 1,91615