2. Analiza widmowa sygnałów okresowych.doc, 1/24
ANALIZA WIDMOWA SYGNAŁÓW OKRESOWYCH
1
Wprowadzenie
• ze względu na duży stopień złożoności i nieregularności sygnałów stosowanych
w praktyce ich przedstawienie w postaci formuły matematycznej i analiza w naturalnej
dziedzinie czasu stają się zazwyczaj niemożliwe i z tego względu posługujemy się
różnego rodzaju reprezentacjami (rodzaj symbolicznego opisu)
• dużego znaczenia nabiera zatem problem reprezentacji analitycznej sygnału, która
z jednej strony prowadzi do uproszczenia analizy a z drugiej strony umożliwia głębszą
interpretację niektórych jego cech fizycznych (np. reprezentacja widmowa sygnału)
• reprezentacja sygnału zawiera pełną informację o sygnale, wyrażoną w inny, zazwyczaj
bardziej abstrakcyjny sposób
• najogólniej rzecz biorąc istnieją dwie podstawowe reprezentacje sygnałów –
reprezentacja dyskretna i reprezentacja ciągła
• reprezentacja dyskretna sygnału (rozwinięcie w szereg Fouriera) umożliwia zastąpienie
badania funkcyjnej zależności w nieprzeliczalnym zbiorze punktów badaniem
przeliczalnego, ale w ogólnym przypadku nieskończonego, zbioru współczynników (liczb
rzeczywistych lub zespolonych)
• reprezentacja ciągła sygnału polega na określeniu odpowiedniego przekształcenia
sygnału (najczęściej całkowego), przyporządkowującemu mu odpowiedniej
reprezentującej go rzeczywistej lub zespolonej funkcji
1
opracowano na podstawie [1-4], wersja z dnia 02.10.2014
materiał nie jest pełnym i ścisłym pod względem formalnym opracowaniem poszczególnych tematów, stanowi
jedynie szkielet, wokół którego budowany jest wykład
2. Analiza widmowa sygnałów okresowych.doc, 2/24
ANALIZA WIDMOWA SYGNAŁÓW OKRESOWYCH
Aproksymacja sygnału
• należy aproksymować sygnał
( )
t
x
przez sygnał
( )
t
u
w przedziale czasu
(
)
2
1
,t
t
, czyli
( )
( )
(
)
2
1
,
,
t
t
t
t
u
a
t
x
∈
≈
mówimy: w przedziale
(
)
2
1
,t
t
sygnał
( )
t
x
ma składową sygnału
( )
t
u
o wartości
a
• należy tak dobrać wartość
a
aby błąd aproksymacji
( ) ( )
( )
t
u
a
t
x
t
x
e
−
=
był w tym przedziale najmniejszy
• miarą jakości aproksymacji jest wartość błędu średniokwadratowego
( )
( )
( )
[
]
( )
∫
∫
−
−
=
−
=
ε
2
1
2
1
2
1
2
2
1
2
1
1
t
t
t
t
e
dt
t
t
u
a
t
x
t
t
dt
t
x
t
t
należy wyznaczyć wartość
a
, przy której
ε
osiąga minimum
2. Analiza widmowa sygnałów okresowych.doc, 3/24
ANALIZA WIDMOWA SYGNAŁÓW OKRESOWYCH
Aproksymacja sygnału (cd)
• po zróżniczkowaniu i przyrównaniu do zera
0
d
d =
ε
a
otrzymujemy
( ) ( )
( )
∫
∫
=
2
1
2
1
2
t
t
t
t
dt
t
u
dt
t
u
t
x
a
jeśli
0
=
a
wówczas oznacza to, że sygnał
( )
t
x
nie zawiera składowej sygnału
( )
t
u
,
że sygnały
( )
t
x
oraz
( )
t
u
są skrajnie do siebie niepodobne, że sygnały
( )
t
x
oraz
( )
t
u
są ortogonalne w przedziale
(
)
2
1
,t
t
• zatem sygnały
( )
t
x
oraz
( )
t
u
są ortogonalne w przedziale
(
)
2
1
,t
t
jeżeli
( ) ( )
0
2
1
=
∫
t
t
dt
t
u
t
x
2. Analiza widmowa sygnałów okresowych.doc, 4/24
ANALIZA WIDMOWA SYGNAŁÓW OKRESOWYCH
Aproksymacja sygnału (cd)
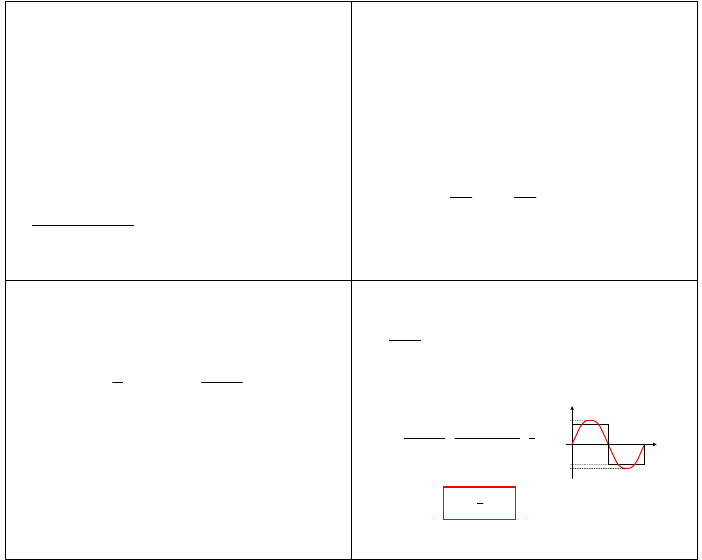
• przykład 1
funkcję prostokątną
( )
t
x
aproksymować przez przebieg sinusoidalny
( )
t
u
,
w przedziale
(
)
π
2
,
0
, minimalizując wartość błędu średniokwadratowego
( )
π
<
<
π
−
π
<
<
=
2
1
0
1
t
t
t
x
dla
dla
,
( )
t
t
u
sin
=
( ) ( )
( )
π
=
−
=
=
∫
∫
∫
∫
∫
π
π
π
π
4
sin
sin
sin
2
0
2
2
0
2
2
1
2
1
tdt
tdt
tdt
dt
t
u
dt
t
u
t
x
a
t
t
t
t
zatem
( )
t
t
x
sin
4
π
≈
4/π
t
x
(t),
0
1
-1
-4/π
u
(t)
π
2π
2. Analiza widmowa sygnałów okresowych.doc, 5/24
ANALIZA WIDMOWA SYGNAŁÓW OKRESOWYCH
Aproksymacja sygnału (cd)
• dla zmniejszenia błędu aproksymacji należy użyć zbioru wzajemnie ortogonalnych
w przedziale czasu
(
)
2
1
,t
t
funkcji
( )
t
u
1
,
( )
t
u
2
, ,
( )
t
u
n
, czyli
( ) ( )
j
i
dt
t
u
t
u
t
t
j
i
≠
=
∫
0
2
1
• zatem sygnał
( )
t
x
będzie zatem aproksymowany w przedziale
(
)
2
1
,t
t
przez liniową
kombinację
n
wzajemnie ortogonalnych funkcji
( )
( )
( )
( )
( )
∑
=
=
+
+
+
≈
n
i
i
i
n
n
t
u
a
t
u
a
t
u
a
t
u
a
t
x
1
2
2
1
1
...
• można wykazać, że jeśli funkcje
( )
t
u
1
,
( )
t
u
2
, ...,
( )
t
u
n
tworzą zbiór zupełny funkcji
wzajemnie ortogonalnych wówczas ze wzrostem
n
średniokwadratowy błąd
aproksymacji maleje w granicy do zera
( )
( )
( )
( )
( )
∑
∞
=
=
+
+
+
+
=
1
2
2
1
1
...
...
i
i
i
n
n
t
u
a
t
u
a
t
u
a
t
u
a
t
x
(równość sygnału i szeregu w sensie wartości błędu średniokwadratowego, nie zawsze
oznacza to zbieżność punktową – efekt Gibbsa)
2. Analiza widmowa sygnałów okresowych.doc, 6/24
ANALIZA WIDMOWA SYGNAŁÓW OKRESOWYCH
Aproksymacja sygnału (cd)
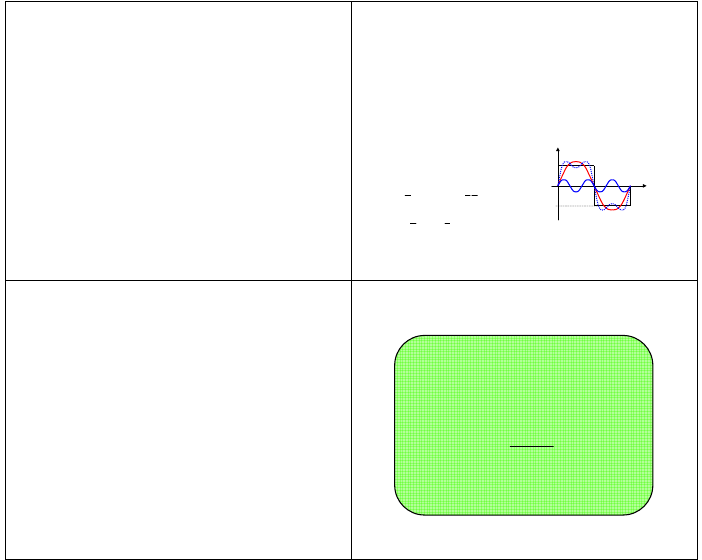
• przykład 2
funkcję prostokątną
( )
t
x
z przykładu 1 aproksymować w przedziale
(
)
π
2
,
0
przez
skończony szereg wzajemnie ortogonalnych funkcji sinusoidalnych
( )
3
,
2
,
1
,
sin
=
=
i
it
t
u
i
, minimalizując wartość błędu średniokwadratowego
≠
=
π
=
=
∫
π
j
i
j
i
jtdt
it
I
0
sin
sin
2
0
dla
dla
warunek wzajemnej ortogonalności
( )
( )
( )
( )
t
u
a
t
u
a
t
u
a
t
x
3
3
2
2
1
1
+
+
≈
( )
t
t
u
sin
1
=
,
( )
t
t
u
2
sin
2
=
,
( )
t
t
u
3
sin
3
=
π
=
4
1
a
,
0
2
=
a
,
π
=
4
3
1
3
a
( )
+
π
≈
t
t
t
x
3
sin
3
1
sin
4
t
x
(t),
0
1
-1
u
1
(t),
π
2π
u
3
(t)
2. Analiza widmowa sygnałów okresowych.doc, 7/24
ANALIZA WIDMOWA SYGNAŁÓW OKRESOWYCH
Uogólniony szereg Fouriera
• z matematycznego punktu widzenia zagadnienie dyskretnej reprezentacji sygnału
sprowadza się do zagadnienia aproksymacji, czyli przybliżenia sygnału
( )
t
x
szeregiem
typu
( )
( )
∑
=
≈
n
i
i
i
t
u
a
t
x
0
gdzie:
( )
t
u
i
- ustalone funkcje czasu (funkcje bazowe)
i
a
- współczynniki szeregu (liczby rzeczywiste lub zespolone)
•
w pierwszym kroku
procedury aproksymacyjnej wybiera się zbiór funkcji
( )
t
u
i
o określonych właściwościach,
w drugim kroku
wyznacza się liczby
i
a
,
tak, aby błąd
aproksymacji był najmniejszy w sensie pewnego ustalonego kryterium miary błędu
(minimum błędu średniokwadratowego)
• funkcje
( )
t
u
i
są dobierane w taki sposób, by ze wzrostem ich liczby
n
błąd
aproksymacji malał i w granicy szereg nieskończony był zbieżny według średniej do
funkcji aproksymowanej
( )
t
x
(zbiór zupełny funkcji wzajemnie ortogonalnych)
2. Analiza widmowa sygnałów okresowych.doc, 8/24
ANALIZA WIDMOWA SYGNAŁÓW OKRESOWYCH
Uogólniony szereg Fouriera (cd)
szereg
( )
( )
∑
∞
=
=
0
i
i
i
t
u
a
t
x
gdzie
( )
{
}
t
u
i
stanowi układ zupełny funkcji wzajemnie ortogonalnych
w przedziale
(
)
2
1
,t
t
, a współczynniki
i
a
określone są zależnością
( ) ( )
( )
∫
∫
=
2
1
2
1
2
t
t
i
t
t
i
i
dt
t
u
dt
t
u
t
x
a
nosi nazwę uogólnionego szeregu Fouriera
2. Analiza widmowa sygnałów okresowych.doc, 9/24
ANALIZA WIDMOWA SYGNAŁÓW OKRESOWYCH
Uogólniony szereg Fouriera (cd)
• podane powyżej definicje można uogólnić na układ ortogonalnych funkcji zespolonych
• warunek ortogonalności dla układu funkcji zespolonych zapisuje się następująco
( ) ( )
,...
2
,
1
,
0
,
,
0
2
1
*
=
≠
=
∫
j
i
j
i
dt
t
u
t
u
t
t
j
i
gdzie
dla
• współczynniki uogólnionego szeregu Fouriera dla układu ortogonalnych funkcji
zespolonych wyznacza się z następującego wzoru
( ) ( )
( )
∫
∫
=
2
1
2
1
2
*
t
t
i
t
t
i
i
dt
t
u
dt
t
u
t
x
a
2. Analiza widmowa sygnałów okresowych.doc, 10/24
ANALIZA WIDMOWA SYGNAŁÓW OKRESOWYCH
Uogólniony szereg Fouriera (cd)
• uogólniony szereg Fouriera posiada bardzo istotną właściwość: zapewnia najlepszą
aproksymację w sensie minimum błędu średniokwadratowego (bez dowodu)
• z powyższego wynika, iż rozwijanie sygnału
( )
t
x
, przy użyciu wybranego układu funkcji
ortogonalnych w uogólniony szereg Fouriera sprowadza się do jednoznacznego
przyporządkowania mu ciągu liczb
n
i
a
a
a
a
a
,...,
,...,
,
,
2
1
0
• możliwość przedstawienia sygnałów w postaci uogólnionego szeregu Fouriera ma bardzo
istotne znaczenie praktyczne; zamiast badać funkcyjne zależności w nieprzeliczalnym
zbiorze punktów, możemy charakteryzować go przeliczalnym (w ogólnym przypadku
nieskończonym) zbiorem współczynników
• Dla przedstawienia sygnału w postaci uogólnionego szeregu Fouriera można stosować
zarówno funkcje elementarne jak i specjalne układy, spełniające warunek ortogonalności
w rozmaitych przedziałach. Mogą to być funkcje trygonometryczne, funkcje typu
x
x
sin
,
wielomiany Hermite’a, Legendre’a, Czebyszewa, funkcje Bessela, Laguerre’a, Walsha
i wiele innych. Do celów analizy wybiera się takie funkcje, które zapewniają najszybszą
zbieżność szeregu, tzn. wymagających najmniejszej liczby wyrazów szeregu, przy
zadanej dokładności przybliżenia.
2. Analiza widmowa sygnałów okresowych.doc, 11/24
ANALIZA WIDMOWA SYGNAŁÓW OKRESOWYCH
Wykładniczy szereg Fouriera
• dowolny sygnał
( )
t
x
można rozwinąć w przedziale
(
)
2
1
,t
t
w uogólniony szereg
Fouriera postaci
( )
( )
∑
∞
=
=
0
i
i
i
t
u
a
t
x
gdzie:
( )
t
u
i
- wybrany układ funkcji ortogonalnych w przedziale
(
)
2
1
,t
t
(funkcje bazowe)
i
a
- współczynniki rozwinięcia
• można wykazać, że zbiór funkcji wykładniczych
{ }
...
,
2
,
1
,
0
,
0
±
±
=
ω
i
e
t
ji
tworzy w przedziale
(
)
0
0
0
,
T
t
t
+
, gdzie
0
0
2
ω
π
=
T
, układ ortogonalny
2. Analiza widmowa sygnałów okresowych.doc, 12/24
ANALIZA WIDMOWA SYGNAŁÓW OKRESOWYCH
Wykładniczy szereg Fouriera (cd)
dowód
warunek ortogonalności dla układu funkcji zespolonych
( ) ( )
m
n
dt
t
u
t
u
t
t
m
n
≠
=
∫
0
2
1
*
dla
zatem
(
)
(
)
∫
∫
∫
+
ω
−
+
ω
−
ω
+
ω
ω
=
=
=
0
0
0
0
0
0
0
0
0
0
0
0
0
0
*
T
t
t
t
m
n
j
T
t
t
t
jm
t
jn
T
t
t
t
jm
t
jn
dt
e
dt
e
e
dt
e
e
I
dla
m
n =
0
0
2
0
0
0
ω
π
=
=
=
∫
+
T
dt
I
T
t
t
dla
m
n ≠
(
)
(
)
(
)
(
)
[
]
0
1
1
1
2
0
0
0
0
0
0
=
−
ω
−
=
ω
−
=
−
π
+
ω
−
m
n
j
T
t
t
t
m
n
j
e
m
n
j
e
m
n
j
I
2. Analiza widmowa sygnałów okresowych.doc, 13/24
ANALIZA WIDMOWA SYGNAŁÓW OKRESOWYCH
Wykładniczy szereg Fouriera (cd)
• zatem dowolny sygnał
( )
t
x
można rozwinąć w przedziale
(
)
0
0
0
,
T
t
t
+
w szereg
(wykładniczy)
( )
∑
∞
−∞
=
ω
ω
ω
ω
−
−
ω
−
−
=
+
+
+
+
+
+
=
i
t
ji
i
t
j
t
j
t
j
t
j
e
a
e
a
e
a
a
e
a
e
a
t
x
0
0
0
0
0
...
...,
2
2
1
0
1
2
2
• współczynniki uogólnionego szeregu Fouriera dla układu ortogonalnych funkcji
zespolonych wyznacza się z następujących wzorów
( ) ( )
( )
( )
( )
∫
∫
∫
∫
∫
+
ω
−
+
ω
−
ω
+
ω
−
+
+
=
=
=
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
2
*
1
T
t
t
t
ji
T
t
t
t
ji
t
ji
T
t
t
t
ji
T
t
t
i
T
t
t
i
i
dt
e
t
x
T
dt
e
e
dt
e
t
x
dt
t
u
dt
t
u
t
x
a
2. Analiza widmowa sygnałów okresowych.doc, 14/24
ANALIZA WIDMOWA SYGNAŁÓW OKRESOWYCH
Wykładniczy szereg Fouriera (cd)
• ostatecznie
przedstawienie dowolnego sygnału
( )
t
x
za pomocą szeregu wykładniczego
( )
∑
∞
−∞
=
ω
ω
ω
ω
−
−
ω
−
−
=
+
+
+
+
+
+
=
i
t
ji
i
t
j
t
j
t
j
t
j
e
a
e
a
e
a
a
e
a
e
a
t
x
0
0
0
0
0
...
...,
2
2
1
0
1
2
2
gdzie
( )
∫
+
=
0
0
0
0
0
1
T
t
t
dt
t
x
T
a
( )
∫
+
ω
−
=
0
0
0
0
0
1
T
t
t
t
ji
i
dt
e
t
x
T
a
nazywamy rozwinięciem sygnału w szereg wykładniczy Fouriera w przedziale
(
)
0
0
0
,
T
t
t
+
2. Analiza widmowa sygnałów okresowych.doc, 15/24
ANALIZA WIDMOWA SYGNAŁÓW OKRESOWYCH
Wykładniczy szereg Fouriera (cd)
• dotychczasowe rozważania dotyczyły przedstawienia dowolnego sygnału
( )
t
x
za
pomocą szeregu w przedziale skończonym
(
)
0
0
0
,
T
t
t
+
poza tym przedziałem sygnał
( )
t
x
oraz odpowiadający mu szereg Fouriera, nie muszą być sobie równe
• jeśli sygnał
( )
t
x
jest okresowy o okresie
0
T
, to można wykazać, że jego rozwinięcie
w szereg dotyczy przedziału nieskończonego
(
)
∞
∞
− ,
przedstawienie sygnału okresowego
( )
t
x
, o okresie
0
T
, za pomocą szeregu
wykładniczego
( )
∑
∞
−∞
=
ω
=
i
t
ji
i
e
a
t
x
0
gdzie
( )
∫
+
=
0
0
0
0
0
1
T
t
t
dt
t
x
T
a
( )
∫
+
ω
−
=
0
0
0
0
0
1
T
t
t
t
ji
i
dt
e
t
x
T
a
nazywamy rozwinięciem sygnału okresowego w szereg wykładniczy Fouriera
w przedziale nieskończonym
(
)
∞
∞
− ,
2. Analiza widmowa sygnałów okresowych.doc, 16/24
ANALIZA WIDMOWA SYGNAŁÓW OKRESOWYCH
Wykładniczy szereg Fouriera (cd)
• współczynniki
i
a
w ogólnym przypadku są wielkościami zespolonymi, które można
zapisać w postaci wykładniczej
i
j
i
i
e
a
a
ϕ
=
wówczas:
i
a
nazywamy widmem amplitudowym
i
ϕ
nazywamy widmem fazowym
a rozwinięcie w szereg wykładniczy Fouriera przyjmie postać
( )
(
)
∑
∑
∑
∞
−∞
=
ϕ
+
ω
∞
−∞
=
ω
ϕ
∞
−∞
=
ω
=
=
=
i
t
i
j
i
i
t
ji
j
i
i
t
ji
i
i
i
e
a
e
e
a
e
a
t
x
0
0
0
• widmo mocy
2
i
i
a
P =
• moc sygnału
( )
t
x
rozwiniętego w wykładniczy szereg Fouriera
( )
∑
∫
∞
−∞
=
+
=
=
i
i
T
t
t
x
a
dt
t
x
T
P
2
2
0
0
0
0
1

2. Analiza widmowa sygnałów okresowych.doc, 17/24
ANALIZA WIDMOWA SYGNAŁÓW OKRESOWYCH
Trygonometryczny szereg Fouriera
• można wykazać, że zbiór funkcji trygonometrycznych
{
}
...
,
2
,
1
,
0
,
sin
,
cos
0
0
=
ω
ω
i
t
i
t
i
tworzy w przedziale
(
)
0
0
0
,
T
t
t
+
, gdzie
0
0
2
ω
π
=
T
, układ ortogonalny zupełny
• zatem dowolny sygnał
( )
t
x
można rozwinąć w przedziale
(
)
0
0
0
,
T
t
t
+
w szereg postaci
( )
( )
( )
(
)
∑
∑
∑
∑
∑
∞
=
∞
=
∞
=
∞
=
∞
=
ω
+
ω
+
=
=
ω
+
ω
=
+
=
1
0
0
0
0
0
0
0
0
0
sin
cos
sin
cos
i
i
i
i
i
i
i
i
is
i
i
ic
i
t
i
b
t
i
a
a
t
i
b
t
i
a
t
u
b
t
u
a
t
x
2. Analiza widmowa sygnałów okresowych.doc, 18/24
ANALIZA WIDMOWA SYGNAŁÓW OKRESOWYCH
Trygonometryczny szereg Fouriera (cd)
• współczynniki rozwinięcia wyznacza się ze wzorów
( ) ( )
( )
∫
∫
+
+
=
0
0
0
0
0
0
2
T
t
t
ic
T
t
t
ic
i
dt
t
u
dt
t
u
t
x
a
,
( ) ( )
( )
∫
∫
+
+
=
0
0
0
0
0
0
2
T
t
t
is
T
t
t
is
i
dt
t
u
dt
t
u
t
x
b
• zatem współczynniki rozwinięcia dla układu funkcji trygonometrycznych
dla
0
=
i
( )
( )
∫
∫
∫
+
+
+
=
=
0
0
0
0
0
0
0
0
0
0
0
1
1
1
T
t
t
T
t
t
T
t
t
dt
t
x
T
dt
dt
t
x
a
2. Analiza widmowa sygnałów okresowych.doc, 19/24
ANALIZA WIDMOWA SYGNAŁÓW OKRESOWYCH
Trygonometryczny szereg Fouriera (cd)
dla
,...
2
,
1
=
i
( )
( )
∫
∫
∫
+
+
+
ω
=
ω
ω
=
0
0
0
0
0
0
0
0
0
0
0
0
2
0
cos
2
cos
cos
T
t
t
T
t
t
T
t
t
i
tdt
i
t
x
T
tdt
i
tdt
i
t
x
a
( )
( )
∫
∫
∫
+
+
+
ω
=
ω
ω
=
0
0
0
0
0
0
0
0
0
0
0
0
2
0
sin
2
sin
sin
T
t
t
T
t
t
T
t
t
i
tdt
i
t
x
T
tdt
i
tdt
i
t
x
b
2. Analiza widmowa sygnałów okresowych.doc, 20/24
ANALIZA WIDMOWA SYGNAŁÓW OKRESOWYCH
Trygonometryczny szereg Fouriera (cd)
• ostatecznie
dowolny sygnał
( )
t
x
można rozwinąć w szereg trygonometryczny
w przedziale
(
)
0
0
0
,
T
t
t
+
( )
(
)
∑
∞
=
ω
+
ω
+
=
1
0
0
0
sin
cos
i
i
i
t
i
b
t
i
a
a
t
x
gdzie:
( )
∫
+
=
0
0
0
0
0
1
T
t
t
dt
t
x
T
a
( )
∫
+
ω
=
0
0
0
0
0
cos
2
T
t
t
i
tdt
i
t
x
T
a
( )
∫
+
ω
=
0
0
0
0
0
sin
2
T
t
t
i
tdt
i
t
x
T
b

2. Analiza widmowa sygnałów okresowych.doc, 21/24
ANALIZA WIDMOWA SYGNAŁÓW OKRESOWYCH
Trygonometryczny szereg Fouriera (cd)
• dla sygnałów okresowych
sygnał okresowy
( )
t
x
, o okresie
0
T
można rozwinąć w szereg
trygonometryczny w przedziale nieskończonym
(
)
∞
∞
− ,
( )
(
)
∑
∞
=
ω
+
ω
+
=
1
0
0
0
sin
cos
i
i
i
t
i
b
t
i
a
a
t
x
gdzie:
( )
∫
+
=
0
0
0
0
0
1
T
t
t
dt
t
x
T
a
( )
∫
+
ω
=
0
0
0
0
0
cos
2
T
t
t
i
tdt
i
t
x
T
a
( )
∫
+
ω
=
0
0
0
0
0
sin
2
T
t
t
i
tdt
i
t
x
T
b
2. Analiza widmowa sygnałów okresowych.doc, 22/24
ANALIZA WIDMOWA SYGNAŁÓW OKRESOWYCH
Trygonometryczny szereg Fouriera (cd)
• jeśli współczynniki rozwinięcia zapiszemy w postaci
i
i
i
c
a
ϕ
= cos
oraz
i
i
i
c
b
ϕ
= sin
wówczas
2
2
i
i
i
b
a
c
+
=
oraz
i
i
i
a
b
arctg
=
ϕ
podstawiając powyższe zależności do wyrażenia na szereg trygonometryczny Fouriera
otrzymamy
( )
(
)
∑
∞
=
ϕ
−
ω
+
=
1
0
0
cos
i
i
i
t
i
c
a
t
x
gdzie:
i
c
- amplituda
i
-tej harmonicznej (
widmo amplitudowe
)
i
ϕ
- faza początkowa
i
-tej harmonicznej (
widmo fazowe
)
2. Analiza widmowa sygnałów okresowych.doc, 23/24
ANALIZA WIDMOWA SYGNAŁÓW OKRESOWYCH
Warunki Dirichleta
• aby sygnał okresowy
( )
t
x
można było rozwinąć w szereg Fouriera musi spełniać tzw.
warunki Dirichleta
warunek 1
sygnał
( )
t
x
musi być bezwzględnie całkowalny (warunek dostateczny)
( )
∞
<
∫
+
0
0
0
T
t
t
dt
t
x
warunek 2
dla dowolnego przedziału czasu o długości
0
T
sygnał
( )
t
x
posiada
skończoną liczbę ekstremów
warunek 3
dla dowolnego przedziału czasu o długości
0
T
sygnał
( )
t
x
posiada
skończoną liczbę punktów nieciągłości
każdy przebieg okresowy, który można wytworzyć w warunkach
eksperymentalnych spełnia warunki Dirichleta
2. Analiza widmowa sygnałów okresowych.doc, 24/24
BIBLIOGRAFIA
1. Izydorczyk J., Płonka G., Tyma G.: Teoria sygnałów. Kompendium wiedzy na temat
sygnałów i metod ich przetwarzania, Helion, Gliwice, 2006
2. Szabatin J.: Podstawy teorii sygnałów. Wydawnictwa Komunikacji i Łączności,
Warszawa, 1982.
3. Baskakow S.I.: Sygnały i układy radiotechniczne. Wydawnictwo Naukowe PWN,
Warszawa, 1991.
4. Lathi B.P.: Systemy telekomunikacyjne. Wydawnictwo Naukowo-Techniczne WNT,
Warszawa, 1972.
Wyszukiwarka
Podobne podstrony:
3 psyg,st www odblokowany
1 psyg,st www odblokowany
4 psyg,st www odblokowany
9 psyg,st www odblokowany
11 psyg,st www odblokowany
7 psyg,st www odblokowany
10 psyg,st www odblokowany
6 psyg,st www odblokowany
3 psyg,st www odblokowany
1 psyg,st www odblokowany
więcej podobnych podstron