1

O

PRACOWANIE DOKUMENTACJI POMIARÓW

WSTĘP TEORETYCZNY DO ĆWICZENIA

LABORATORYJNEGO

Nieodzowną częścią każdego eksperymentu me-

trologicznego jest sporządzenie właściwej jego do-
kumentacji. Z uwagi na różnorodność zadań pomia-
rowych, wyposażenia i organizacji pracy danego
laboratorium, nie jest możliwe podanie tylko jedne-
go, szczegółowego schematu postępowania przy jej
wykonywaniu; można jedynie sformułować pewne
zalecenia, które w miarę możliwości powinny być
spełnione. Z reguły zbiór podstawowych dokumen-
tów obejmuje wypełniany w trakcie wykonywania
pomiarów protokół oraz sporządzone na jego pod-
stawie sprawozdanie lub raport, stanowiące osta-
teczne podsumowanie przeprowadzonego ekspery-
mentu.

1.

P

ROTOKÓŁ POMIARÓW

Protokół pomiarowy jest dokumentem, który na-

leży prowadzić na bieżąco z wykorzystaniem wcze-
ś

niej przygotowanego formularza. Powinien on być

zwięzły, ale jednocześnie zawierać taką ilość infor-
macji o przeprowadzanym eksperymencie i warun-
kach w jakich się on odbywał, aby mógł być zrozu-
miały przez inne osoby nie biorące bezpośredniego
udziału w pomiarach.

Wyniki odczytane z przyrządów powinny być

natychmiast notowane. Z uwagi na możliwość po-
wstania błędów, niedopuszczalne jest jakiekolwiek
przeliczanie ich w pamięci przed wpisaniem do
protokołu. Kolejność czynności powinna być nastę-
pująca: odczyt – zapis – sprawdzenie odczytu z
zapisem. Niewskazane jest również przepisywanie
protokołu, głównie ze względu na powstające wów-
czas pomyłki, przeinaczenia, pomijanie tych wyni-
ków, które wydają się mniej ważne lub błędne. Na
odrzucenie danego wyniku można decydować się
dopiero na etapie ostatecznego sprawozdania, po

wykonaniu stosownych obliczeń i rozważeniu
wszystkich warunków wykonania eksperymentu.

Mimo wymogów wypełniania na bieżąco, proto-

kół powinien być prowadzony starannie. Niechlujne
lub nieczytelne notowanie wyników jest częstym
powodem błędnych interpretacji i świadczy o niskiej
kulturze technicznej eksperymentatora.

Do podstawowych informacji, które z reguły

powinny znaleźć się w każdym protokole należą:
1)

dane dotyczące osoby lub osób przeprowadza-
jących pomiary, miejsce, data i temat, zestawio-
ne najczęściej w formie odpowiedniej tabeli na-
główkowej,

2)

cel pomiarów,

3)

niezbędne dane teoretyczne o przeprowadza-
nych pomiarach (jeśli wymagane),

4)

wykaz aparatury, najlepiej sporządzony w for-
mie odpowiedniej tabeli, np. tabela 1,

Tabela 1.

Przykład wykazu aparatury

Lp.

Nazwa i

typ przy-

rządu

Numer punktu

pomiarowego

Oznaczenie

na schema-

cie

Uwagi

5)

ponumerowane schematy układów pomiaro-
wych, umieszczone pod odpowiednimi punkta-
mi pomiarowymi,

6)

wyniki pomiarów sporządzone, o ile to jest
tylko możliwe, w postaci tabeli zaopatrzonej w
numer i tytuł – np. tabela 2. Tabela jest najbar-
dziej jasną i zwartą formą zapisu. Każda ko-
lumna lub każdy wiersz w tabeli powinny być
oznaczone symbolem wielkości, której wartości
one zawierają, symbolem jednostki, w której te
wartości są podawane oraz numerem porząd-
kowym.

2

Tabela 2.

Wyniki pomiaru pewnej charaktery-

styki częstotliwościowej

U

z

=

±

15V

Lp.

f

U

1

U

2

-

Hz

mV

mV

1

1

100

238

2

10

100

241

3

100

100

239

4

1000

100

175

Wartość uzyskana z pomiaru jest zawsze liczbą
przybliżoną (trudno wyobrazić sobie przyrząd po-
miarowy z wyświetlaczem kilkunastopozycyjnym).
Stopień tego przybliżenia określa liczba tzw. cyfr
znaczących. Cyframi znaczącymi są cyfry 0

÷

9, przy

czym liczy się je począwszy od pierwszej cyfry
nierównej zeru z lewej strony; np. liczba 0,0067 ma
dwie cyfry znaczące, zaś liczba 156,08 – pięć cyfr
znaczących. Dla zaznaczenia ilości cyfr znaczących,
wygodnie jest posługiwać się mnożnikiem 10

n

lub

stosować odpowiednie jednostki pochodne danej
wielkości. W tabeli 3 zestawiono przykłady określa-
nia cyfr znaczących.

Tabela 3.

Przykłady cyfr znaczących

Wartość liczbowa

Liczba cyfr znaczących

812

trzy

1520 = 1,52

⋅

10

3

trzy

0,032 = 32

⋅

10

-3

dwie

0,320 = 32

⋅

10

-2

dwie

Może się jednak zdarzyć, że w pewnej sytuacji

należy uwzględnić także zero podane na ostatniej
pozycji wartości liczbowej. Sytuacja taka nastąpi
jeśli będziemy mieli do czynienia z serią pomiaro-
wą, w której jeden z wielu z wyników kończy się
zerem. Zapis wszystkich wyników powinien się
odbywać z dokładnością do tej samej liczby miejsc
znaczących. Stosowanie się do tej zasady daje pew-
ność - jaka jest wartość ostatniej cyfry znaczącej i
nie ma obaw, że wpisujący zapomniał ją na przykład
dopisać. Przykład pokazano w tabeli 4.

Tabela 4.

Przykład zapisu serii pomiarów

Zły zapis serii pomia-

rowej

Dobry zapis serii po-

miarowej

1234,1
1234,4
1235,1
1234
1234,2

1234,1
1234,4
1235,1
1234,0
1234,2

2.

S

PRAWOZDANIE

Sprawozdanie (lub inaczej raport) z przeprowa-

dzonych pomiarów tworzy się na podstawie orygi-
nalnego protokołu pomiarów. W zależności od wy-
magań stawianych autorowi, może ono przybierać
różne formy. Najczęściej jednak obejmuje następu-
jące części składowe:
1)

tabelę nagłówkową zawierająca dane o autorze,
dacie wykonania i tytuł,

2)

streszczenie będące zwięzłą prezentacją całej
treści,

3)

krótki opis podstaw teoretycznych przeprowa-
dzanego doświadczenia (lub doświadczeń przy-
pisanych do odpowiednich punktów pomiaro-
wych protokołu) z uwzględnieniem zwięzłej
prezentacji zastosowanych metod pomiarowych,

4)

opracowane wyniki pomiarów – wyniki wyko-
nanych obliczeń, przykładowe obliczenia, wy-
kresy,

5)

dyskusję otrzymanych wyników.

Opracowanie wyniku pomiaru polega na podaniu

pary liczb: najbardziej prawdopodobnej wartości
wielkości mierzonej oraz przedziału zwanego błę-
dem, w którym z określonym prawdopodobień-
stwem zawiera się rzeczywista wartość mierzonej
wielkości. Ich poprawne wyznaczenie warunkowane
jest znajomością podstawowych pojęć i zasad ra-
chunku błędów występujących w pomiarach.

2.1. Klasyfikacja bł

ę

dów i podstawowe

oznaczenia.

Każdy pomiar jest obarczony błędem i każdy

eksperymentator ma obowiązek oszacować jego
poziom. W innym przypadku pomiar jest niewiary-
godny gdyż pojęcia pomiar i błąd są nierozerwalne.

Przyczyny powstawania błędów mogą być różne

i mogą mieć różny charakter. W związku z tym
błędy można podzielić na przypadkowe, systema-
tyczne, nieczułości i nadmierne (tzw. grube).

Błędy przypadkowe – spowodowane są oddzia-

ływaniem na układ pomiarowy wielu niezależnych
czynników, które zmieniają się w czasie w trudny do
przewidzenia sposób, oraz subiektywnych właści-
wości osób wykonujących pomiar.

Błędy systematyczne – spowodowane są oddzia-

ływaniem na układ pomiarowy czynników, które
podczas pomiaru są stałe lub zmieniają się według
określonej zależności.

Błędy nadmierne – ich charakter jest w zasadzie

podobny do błędów przypadkowych, ale ze względu
na znaczną różnicę wartości dokonuje się ich zróżni-
cowania, a wyniki pomiarów nimi obarczone odrzu-
ca się.

Błędy nieczułości – występują tylko przy pomia-

rach przeprowadzanych metodami zerowymi, przy
których wykorzystuje się wskaźniki równowagi
charakteryzujące się pewną właściwością nazywaną
czułością przyrządu (zdolność przyrządu do reago-
wania na zmianę wartości wielkości mierzonej do-
piero powyżej pewnej minimalnej wartości tej wiel-
kości).

Błąd jest miarą określającą jak bardzo wynik

pomiaru różni się od wartości rzeczywistej mierzo-
nej wielkości.

Różnicę między wartością uzyskaną z pomiaru

X

m

, a wartością rzeczywistą X

r

mierzonej wielkości

nazywamy błędem bezwzględnym

∆

X i zapisujemy

w postaci:

r

m

X

X

X

−

=

∆

(1)

3

Błąd bezwzględny jest wyrażany w jednostkach

miary mierzonej wielkości. Jeżeli jest to możliwe,
można go wyeliminować przez zastosowanie po-
prawki p o znaku przeciwnym:

X

p

∆

−

=

(2)

Błąd względny (rzeczywisty)

δ

X

jest stosunkiem

błędu bezwzględnego do wartości rzeczywistej mie-
rzonej wielkości:

r

X

X

X

∆

=

δ

(3)

Błąd względny (procentowy)

δ

%

X

jest równy błę-

dowi względnemu wyrażonemu w procentach:

%

100

%

⋅

∆

=

r

X

X

X

δ

(4)

Dokładność przyrządu pomiarowego jest wyra-

ż

ana za pomocą klasy dokładności przyrządu lub za

pomocą błędu podstawowego (względnego) albo
bezwzględnego błędu podstawowego

przyrządu (w

przypadku przyrządów z odczytem analogowym), a
w przypadku przyrządów z odczytem cyfrowym
tylko za pomocą bezwzględnego błędu podstawo-
wego

.

Klasa dokładności przyrządu pomiarowego jest

wyznaczana na podstawie jego błędu podstawowego
wyrażanego w procentach, obliczanego jako stosu-
nek maksymalnej wartości bezwzględnego błędu
pomiaru i wartości nominalnej zakresu pomiarowe-
go. Klasą analogowego przyrządu pomiarowego jest
najmniejsza z liczb należąca do ciągu liczbowego
określonego przez Polską Normę i spełniającą za-
leżność:

%

100

.

max

%

⋅

∆

=

≥

N

g

X

X

X

d

kl

δ

(5)

Zgodnie z PN-92/E-06501/01 ustalono, że do

określenia klasy elektrycznych i elektronicznych
analogowych przyrządów pomiarowych stosować
należy wartości liczbowe z ciągu (1;2;5)

⋅

10

-n

- gdzie

n oznacza liczbę całkowitą. Ponadto dopuszcza się
klasy 0,3; 1,5; 2,5; 3.

Jak wspomniano wyżej, dokładność przyrządu

pomiarowego może być także określana za pomocą
bezwzględnego błędu podstawowego

przyrządu

pomiarowego

∆

g

X

. Błąd ten w zależności od produ-

centa może być zdefiniowany na różne sposoby:

.)

.

.

%

.

.

%

(

n

z

w

b

m

w

a

X

g

+

±

=

∆

(6)

.

.

.

%

n

z

w

c

X

g

±

=

∆

(7)

.

.

%

m

w

d

X

g

±

=

∆

,

(8)

gdzie: w.m.=X

m

– wartość mierzona; w.z.n. = X

N

–

wartość nominalna zakresu; a, b, c, d – wartości
liczbowe (wyrażone w %) charakterystyczne dla
danego przyrządu (c – klasa lub błąd podstawowy
względny).

Dla cyfrowych przyrządów pomiarowych nie

wyznacza się klasy, ponieważ w ich przypadku w

grę wchodzi jeszcze błąd dyskretyzacji wynoszący

±

1 kwant wielkości mierzonej. Błąd ten wynika z

zasady działania cyfrowych przyrządów pomiaro-
wych (zamiana wielkości ciągłej w dyskretną) i nie
da się go wyeliminować.

Bezwzględny błąd podstawowy pomiaru przy-

rządem cyfrowym podawany jest w jednej z dwóch
postaci:

)

(

b

a

X

g

+

±

=

∆

(9)

a

X

g

±

=

∆

,

(10)

gdzie: a – składowa analogowa błędu (zależna od
„klasy” przyrządu cyfrowego), b – składowa cyfro-
wa błędu.

Składowa analogowa błędu jest wyrażana w

przyrządach cyfrowych za pomocą wyrażenia (6).
Natomiast składowa cyfrowa wynosi 1 kwant na
ostatniej pozycji wyświetlacza (niektóre publikacje
podają 0,5 kwanta). Bardzo często producenci apara-
tury pomiarowej pomijają ten błąd w danych katalo-
gowych (wyrażenie (10)), ponieważ jest on zwykle
2

÷

5 razy mniejszy niż błąd analogowy (czasem

więcej).

W niektórych przypadkach równość (6) jest

przedstawiana dla przyrządów cyfrowych w postaci:

)

.

.

%

(

n

m

w

a

X

g

+

±

=

∆

,

(11)

gdzie: n – liczba cyfr (całkowita). n może przyjmo-
wać wartości od 1 do kilkuset.

Względny błąd pomiaru (dokładność pomiaru)

będzie określony jako stosunek bezwzględnego
błędu pomiaru do wartości wielkości mierzonej co
można zapisać w następujący sposób:

%

100

%

⋅

∆

=

m

g

X

X

X

δ

.

(12)

Jeżeli porównamy wyrażenie (12) z wyrażeniami

(6), (7), (11) to widać, że względny błąd pomiaru
jest tym większy im większy jest stosunek wartości
zakresu nominalnego przyrządu pomiarowego do
wartości mierzonej.

W dalszej części ograniczymy się do bliższego

zaprezentowania najczęściej występujących rodza-
jów błędów – przypadkowych i systematycznych.

2.2. Bł

ę

dy przypadkowe

Błędu przypadkowego nie można uwzględnić ja-

ko poprawki w wyniku pomiaru. Można tylko na
podstawie serii pomiarów wykonanych w tych sa-
mych warunkach (ten sam przyrząd, eksperymenta-
tor, warunki klimatyczne itd.) ustalić z określonym
prawdopodobieństwem granice tego błędu. Posługu-
jąc się metodami statystycznymi można oszacować
jego wpływ na wynik pomiaru.

Z uwagi na fakt, że wyniku pomiaru obarczone-

go błędem przypadkowym nie da się przewidzieć,
przyjmuje się, że jest on zmienną losową (najczę-
ś

ciej ciągłą). W procesie pomiaru zmienna ta przyj-

muje tylko jedną konkretną wartość; z określonym
prawdopodobieństwem możliwe są jednak również

4

wartości inne. Ze względu na potwierdzone do-
ś

wiadczalnie założenia mówiące, że przy odpowied-

nio dużej liczbie pomiarów (n>30):

•

błędy równe co do wartości bezwzględnej, ale o
przeciwnych znakach zdarzają się jednakowo
często,

•

prawdopodobieństwo wystąpienia błędu dodat-
niego równe jest prawdopodobieństwu wystą-
pienia błędu ujemnego,

•

częstość występowania błędów małych jest
większa niż błędów dużych,

•

błędy są zdarzeniami niezależnymi,

zmienna losowa X tworząca wynik pomiaru charak-
teryzuje się ściśle określonym rozkładem funkcji
gęstości prawdopodobieństwa, zwanym rozkładem
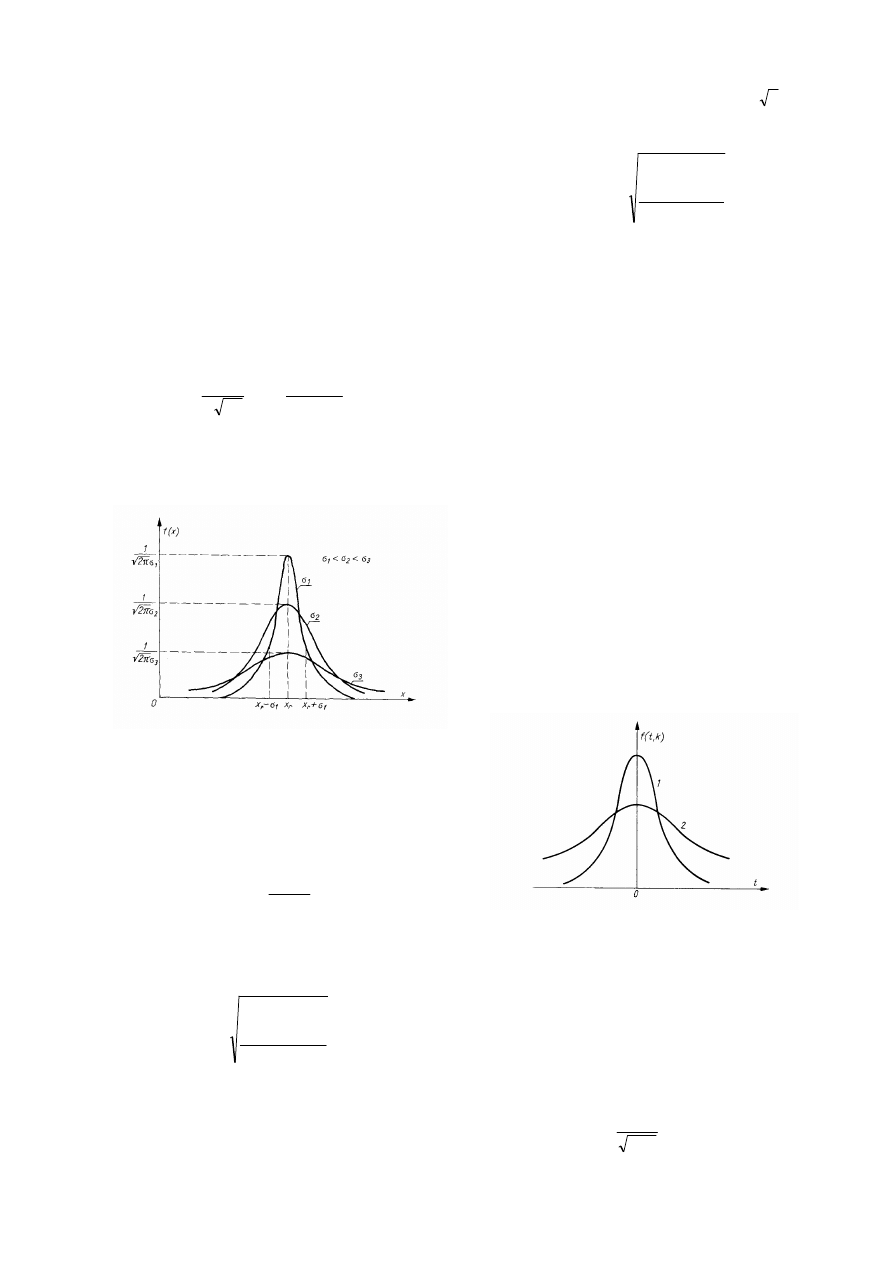
Gaussa (rys. 1):

( )

(

)















−

−

=

2

2

2

exp

2

1

σ

π

σ

r

x

x

x

f

,

(13)

w którym jako x

r

traktuje się wartość rzeczywistą

wartości mierzonej. Parametr

σ

>0 jest miarą rozrzu-

tu wartości tak określonej zmiennej losowej i nosi
nazwę odchylenia standardowego.

Podczas wykonywania pomiarów wartość rzeczywi-
sta x

r

wielkości mierzonej nie jest znana, ale można

wykazać, ze jej wartością najbardziej prawdopodob-
ną ze statystycznego punktu widzenia jest średnia
arytmetyczna serii n pomiarów:

n

X

X

n

i

i

s

∑

=

=

1

.

(14)

Drugi parametr rozkładu zmiennej losowej jako
wyniku pomiaru, odchylenie standardowe

σ

,

przy

dostatecznie dużej liczbie pomiarów n>30 może być
wyznaczony ze wzoru:

(

)

1

1

2

−

−

=

∑

=

n

X

x

n

i

s

i

σ

(15)

jako średni kwadratowy błąd pojedynczego pomiaru.
Oczywiście samą średnią arytmetyczną X

s

serii po-

miarów można też traktować jako zmienną losową
(licząc średnie z kilku serii pomiarowych uzyskuje
się różniące się wartości). Teoria prawdopodobień-
stwa stwierdza, że odchylenie standardowe średniej

(średni kwadratowy błąd średniej) jest

n razy

mniejszy od odchylenia standardowego pojedyncze-
go pomiaru:

(

)

( )

1

1

2

−

−

=

∆

=

∑

=

n

n

X

x

X

n

i

s

i

s

sp

s

σ

.

(16)

Powyższy parametr jako miara rozrzutu średniej ma
istotny sens fizyczny, gdyż wyznacza prawdopodo-
bieństwo z jakim wartość rzeczywista x

r

zawiera się

w przedziale (X

s

−

t

σ

s

, X

s

+t

σ

s

). Przedział ten nosi

nazwę przedziału ufności, a prawdopodobieństwo
mu odpowiadające nazywa się poziomem ufności.
Charakterystycznymi przedziałami ufności i odpo-
wiadającymi im poziomami ufności są:
dla t=1 P(X

s

−σ

s

< x

r

< X

s

+

σ

s

)=0,6826,

dla t=2 P(X

s

−

2

σ

s

< x

r

< X

s

+

2

σ

s

)=0,9546,

dla t=3 P(X

s

−

3

σ

s

< x

r

< X

s

+

3

σ

s

)=0,9974.

Przedział

±

3

σ

s

oznacza więc, że wystąpi w nim

99.74% wszystkich wyników obarczonych błędami
przypadkowymi. Prawdopodobieństwo wystąpienia
błędu przypadkowego o module większym niż 3

σ

s

jest więc bardzo małe. Przedział:

s

sp

s

gp

X

X

∆

⋅

=

∆

3

(17)

jest granicznym błędem przypadkowym wartości
ś

redniej, zwanym też granicznym przedziałem ufno-

ś

ci.

Należy jednak pamiętać, że zależność na

∆

sp

X

s

jest

słuszna pod warunkiem dużej liczby powtórzeń
pomiarów (teoretycznie n

→∞

). Przy liczbie pomia-

rów n=3

÷

20 wynik pomiaru jako zmienna losowa

ma rozkład Studenta. Rozkład ten jest szerszy i bar-
dziej spłaszczony od rozkładu Gaussa – rys. 2.

Zależy on jednak od liczby pomiarów i przy n>30
przyjmuje praktycznie kształt krzywej Gaussa. Przy
wyznaczaniu przedziału ufności z rozkładu Studenta
korzysta się z odpowiednich tablic lub stosuje się
przybliżenie w postaci skorygowanego wzoru na

∆

sp

X

s

rozkładu Gaussa:

∆

’

sp

X

s

=k’

∆

sp

X

s

,

(18)

gdzie:

1

1

1

'

−

+

=

n

k

.

(19)

Rys. 1. Przykłady funkcji Gaussa.

Rys. 2. Postać rozkładu Gaussa (1) i Studenta (2)

przy ustalonej liczbie pomiarów k.

5

Zależność na

∆

gp

X

s

pozostaje bez zmian.

2.3. Bł

ę

dy systematyczne

Błędy systematyczne mają decydujący wpływ na

wynik pomiaru. Można je podzielić na następujące
grupy:

•

błędy przyrządów pomiarowych;

•

błędy metody pomiarowej lub układu po-
miarowego;

•

błędy wywołane czynnikami zakłócającymi
o stałej wartości w czasie lub zmieniające
się zgodnie ze znaną zależnością.

Jednym z głównych zadań eksperymentatora jest

minimalizacja tych właśnie błędów. Błędy pierwszej
grupy można jedynie ograniczać przez zastosowanie
coraz dokładniejszych przyrządów, ale stosowanie
przyrządów dokładnych (dobrych) jest drogie. W
związku z tym przystępując do planowania jakiegoś
eksperymentu (przygotowując się do pomiaru) nale-
ż

y bardzo wnikliwie zastanowić się nad możliwością

eliminacji lub przynajmniej znacznego ograniczenia
błędów należących do pozostałych dwóch grup (np.
przez wyliczenie odpowiednich poprawek i zasto-
sowanie ich).

Podstawowym parametrem opisującym dokład-

ność przyrządu pomiarowego jest graniczny syste-
matyczny błąd przyrządu obliczany z zależności:

N

gs

X

d

kl

X

%

100

)

.

(

=

∆

(20)

lub za pomocą wzorów (6), (7), (8) oraz (9) i (11).
Wyrażenie (20) jest tożsame wyrażeniu (7). Przy
założeniu równomiernego rozkładu błędu systema-
tycznego w przedziale

±∆

gs

X

można też wykazać, że

ś

redni kwadratowy błąd systematyczny jest równy:

3

X

X

gs

ss

∆

=

∆

(21)

2.4. Bł

ę

dy w pomiarach po

ś

rednich

W eksperymentach pomiarowych spotkać można

dwa rodzaje pomiarów: pomiar bezpośredni, gdy
wartość wielkości mierzonej jest określona na pod-
stawie wskazania jednego przyrządu i pomiar po-
ś

redni, gdy wyznaczana wielkość Y jest funkcją

kilku

innych

wielkości

pomocniczych

X

i

:

Y

=f(X

1

, X

2

,..., X

n

). Rozważmy ten drugi rodzaj po-

miarów.

Chcemy wiedzieć, jakim błędem wypadkowym

∆

Y

będzie obciążona wielkość Y, przy znanych błę-

dach wielkości pośrednich X

i

. Najczęściej stosowaną

metodą szacowania tego błędu, zarówno w odniesie-
niu do błędów systematycznych i przypadkowych,
jest wykorzystanie pewnej tożsamości matematycz-
nej zwanej rozwinięciem funkcji w szereg Taylora
[1][3][4]. Ograniczając się do funkcji dwu zmien-
nych powyższe rozwinięcie ma postać:

(

) (

)

.

,

,

2

2

1

1

2

1

2

2

1

1

X

X

Y

X

X

Y

X

X

Y

X

X

X

X

Y

Y

Y

∆

∂

∂

+

∆

∂

∂

+

+

≈

∆

+

∆

+

=

=

∆

+

(22)

gdzie

∆

X

1

i

∆

X

2

są przyrostami X

1

i X

2

a

n

n

n

n

X

Y

X

Y

2

1

/

i

/

∂

∂

∂

∂

są tzw. pochodnymi cząstko-

wymi Y względem X

1

i X

2

. Oznacza to, że

n

n

X

Y

1

/

∂

∂

jest wynikiem różniczkowania Y wzglę-

dem X

1

przy ustalonym X

2

, a

n

n

X

Y

2

/

∂

∂

to wynik

różniczkowania Y względem X

2

przy ustalonym X

1

.

Obie pochodne obliczane są w punkcie (X

1

,X

2

).

Stąd błąd bezwzględny:

2

2

1

1

X

X

Y

X

X

Y

Y

∆

∂

∂

+

∆

∂

∂

=

∆

,

(23)

a błąd względny:

.

2

2

1

1

Y

X

X

Y

Y

X

X

Y

Y

Y

Y

∆

∂

∂

+

∆

∂

∂

=

∆

=

δ

(24)

W przypadku, gdy wielkości pomocniczych okre-
ś

lonych z błędami jest więcej, korzysta się z rozwi-

nięcia w szereg Taylora funkcji kilku zmiennych.
Błąd bezwzględny pomiaru wielkości Y można
wówczas przedstawić w następujący sposób:

n

n

X

X

Y

X

X

Y

X

X

Y

Y

∆

∂

∂

+

+

∆

∂

∂

+

∆

∂

∂

=

∆

...

2

2

1

1

. (25)

Pouczające jest wyznaczenie tego błędu dla dwu

elementarnych pomiarów pośrednich. Jeżeli np.

(

)

2

1

2

1

,

X

X

X

X

Y

+

=

,

(26)

to obie pochodne cząstkowe:

1

2

1

=

∂

∂

=

∂

∂

X

Y

X

Y

.

(27)

Wówczas zgodnie z (25):

∆

Y

≈

∆

X

1

+

∆

X

2

(28)

I drugi przykład – jeżeli:

(

)

2

1

2

1

,

X

X

X

X

Y

⋅

=

,

(29)

to pochodne cząstkowe mają postać:

1

2

2

1

i

X

X

Y

X

X

Y

=

∂

∂

=

∂

∂

.

(30)

A zatem błąd bezwzględny wynosi:

2

1

1

2

X

X

X

X

Y

∆

⋅

+

∆

⋅

=

∆

,

(31)

a błąd względny:

2

1

2

2

1

1

2

1

2

1

2

1

1

2

2

1

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

Y

Y

Y

Y

δ

δ

δ

+

=

∆

+

∆

=

=

⋅

∆

⋅

+

⋅

∆

⋅

=

=

⋅

∆

=

∆

=

(32)

Uzyskaliśmy więc dwie proste reguły wyznaczania
błędów w pomiarach pośrednich: 1) błąd bez-
względny sumy kilku wielkości jest sumą błędów
bezwzględnych każdej z nich oraz 2) błąd względny
iloczynu kilku wielkości jest sumą błędów względ-
nych każdej z nich. Według wzoru (25), określają-
cego tzw. model propagacji (przenoszenia) błędów,
możliwe jest wyznaczenie błędu dla dowolnej zależ-

6

ności funkcyjnej. Przykłady najczęściej spotykane
przedstawia tabela 5:

Tabela 5.

Przykłady propagacji błędów.

Funkcja

Sposób propagacji błędu

y = ax

∆

Y = a

∆

X

y = ax, X

ś

r

≠

0

δ

y =

δ

x

y = x

a

, X

ś

r

≠

0

δ

y = a

δ

x

y = e

x

, Y

ś

r

≠

0

δ

y =

∆

X

y = lnx , X

ś

r

> 0

∆

Y =

δ

x

y = x

1

+ x

2

∆

Y =

∆

X

1

+

∆

X

2

y = x

1

- x

2

∆

Y =

∆

X

1

+

∆

X

2

y = x

1

⋅

x

2

δ

Y =

δ

X

1

+

δ

X

2

y = x

1

/ x

2

δ

Y =

δ

X

1

+

δ

X

2

∑

=

=

n

i

i

i

x

a

y

1

∑

=

∆

=

∆

n

i

i

i

x

a

y

1

∏

=

=

n

i

a

i

i

x

y

1

∑

=

=

n

i

i

i

x

a

y

1

δ

δ

Dotychczas milcząco zakładaliśmy, że błędy

wielkości pomocniczych

∆

X

1

,

∆

X

2

,...,

∆

X

n

są do-

kładnie znane. W praktyce pomiarowej sytuacja taka
jednak nigdy nie występuje. Analizując błędy przy-
padkowe, zależność (25) można przepisać w postaci:

(

)

(

)

(

)

,

...

2

2

1

1

1

1

nr

n

n

r

r

r

X

X

X

Y

X

X

X

Y

X

X

X

Y

Y

Y

−

∂

∂

+

+

−

∂

∂

+

+

−

∂

∂

=

−

(33)

w której indeks „r” odnosi się do wartości oczeki-
wanych a Y, X

1

, X

2

,..., X

n

są zmiennymi losowymi

(można za nie podstawić wartości uzyskane w serii
pomiarowej). Można wykazać [1][3][4], że odchyle-
nie średnie kwadratowe średniej arytmetycznej

∆

sp

Y

s

wyraża się zależnością:

(

)

(

)

(

)

.

]

...

...

[

2

1

2

2

2

2

2

2

2

1

2

1

ns

sp

n

s

sp

s

sp

s

sp

X

X

Y

X

X

Y

X

X

Y

Y

∆













∂

∂

+

+

∆













∂

∂

+

+

∆













∂

∂

=

∆

(34)

W przypadku błędów systematycznych konkret-

ne wartości błędów wielkości pomocniczych rów-
nież nie są znane. Znane są za to granice, w których
te błędy są zawarte. W takich wypadkach oblicza się
ekstremalną możliwą wartość błędu pomiaru po-
ś

redniego, związaną z przyjęciem przez wszystkie

jego składniki tego samego znaku. Jest to tzw. błąd
najgorszego przypadku lub błąd graniczny pomiaru
pośredniego i opisuje się go następująco:

.

...

...

2

2

1

1

ns

sp

n

s

sp

s

sp

g

X

X

Y

X

X

Y

X

X

Y

Y

∆

∂

∂

+

+

+

∆

∂

∂

+

∆

∂

∂

=

∆

(35)

Jeżeli jednak wielkość mierzona zależy od wielu
wielkości pomocniczych, to istnieje wówczas bardzo
małe prawdopodobieństwo takiego zdarzenia, że ich
błędy systematyczne będą przyjmowały wartości
graniczne i niekorzystny układ znaków. Liczenie
błędów według zależności (35) prowadzi więc do
wyniku zawyżonego. Przy założeniu wzajemnej
niezależności błędów wielkości pomocniczych moż-
na wykazać [1], że błąd pomiaru pośredniego można
obliczać tak, jak błąd przypadkowy. Bezwzględny
błąd graniczny pomiaru pośredniego oblicza się
wtedy ze wzoru:

(

)

(

)

(

)

,

]

...

...

[

2

1

2

2

2

2

2

2

2

1

2

1

ns

g

n

s

g

s

g

g

X

X

Y

X

X

Y

X

X

Y

Y

∆













∂

∂

+

+

∆













∂

∂

+

+

∆













∂

∂

=

∆

(36)

gdzie

∆

g

X

i

jest błędem granicznym pomiaru wielko-

ś

ci X

i

.

2.5. Zasady obliczania bł

ę

dów

Ze względu na wymaganą dokładność, pomiary

można podzielić na laboratoryjne (

δ

%

X

<0,05%),

laboratoryjne

ś

redniej

dokładności

(0,05%

≤δ

%

X

≤

0,5%) i techniczne (

δ

%

X

>0,5%). W

zależności od tego do rachunku błędów podchodzi
się z różną precyzją.

2.5.1. Pomiary techniczne.

Pomiar danej wielkości odbywa się na ogół

jednokrotnie a błąd ma na ogół charakter systema-
tyczny ograniczony dokładnością użytych przyrzą-
dów
a)

Pomiar bezpośredni:

-

Obliczamy graniczny błąd pomiaru na podsta-
wie wyrażeń (6), (7), (8), (11) lub (20).

-

Wynik pomiaru zapisujemy w postaci:

X

X

X

g

m

r

∆

±

=

(37)

-

Dokładność pomiaru oblicza się na podstawie
wyrażenia (12).

b)

Pomiar pośredni:

-

Funkcja opisująca wielkość mierzoną ma po-
stać:

)

,....,

(

1

n

X

X

f

Y

=

a

)

,....,

(

1

mn

m

m

X

X

f

Y

=

.

-

Graniczny błąd pomiaru określony jest zależno-
ś

cią (36):

7

∑

=

∆

∂

∂

=

∆

n

i

i

g

i

g

X

X

Y

Y

1

2

lub w postaci uproszczonej (błąd najgorszego
przypadku – zależność (35)) jako :

∑

=

∆

∂

∂

=

∆

n

i

i

g

i

g

X

X

Y

Y

1

gdzie:

∆

g

X

i

– błąd graniczny i-tej wielkość mie-

rzonej bezpośrednio określony tak jak w przy-
padku pomiarów bezpośrednich.

-

Wynik pomiaru zapisujemy w postaci:

Y

Y

Y

g

m

r

∆

±

=

(38)

-

Dokładność pomiaru jest równa:

%.

100

%

⋅

∆

=

m

g

Y

Y

Y

δ

(39)

2.5.2. Pomiary laboratoryjne.

Przy wyliczaniu błędu granicznego pomiaru na-

leży uwzględnić wszystkie typy błędów, zarówno
systematyczne jak i przypadkowe (oraz nieczułości
jeżeli wymaga tego użyta metoda). Pomiary bardzo
dokładne charakteryzują się dużą liczbą powtórnych
pomiarów (długa seria pomiarowa) rzędu 10

÷

20 a

nawet więcej. Długość serii pomiarowej przy pomia-
rach o średniej dokładności wynosi 3

÷

10 pomiarów.

Poniżej omówiony zostanie sposób obliczania błę-
dów pomiaru dla badań laboratoryjnych o średniej
dokładności.
a)

Pomiar bezpośredni:

-

Oblicza się wartość średnią X

s

ze wzoru (14);

-

Błąd średni przypadkowy wartości średniej

∆

sp

X

s

wyznacza się z zależności (16);

-

Określa się błąd graniczny przypadkowy warto-
ś

ci średniej

∆

gp

X

s

z równania (17);

-

Wylicza się błąd graniczny systematyczny

∆

gs

X

na podstawie zależności (20);

-

Korzystając ze wzoru (40) oblicza się granicz-
ny błąd pomiaru

2

2

)

(

)

(

X

X

X

gs

s

gp

g

∆

+

∆

=

∆

(40)

-

Wynik pomiaru zapisuje się w postaci:

X

X

X

g

s

r

∆

±

=

(41)

-

Dokładność pomiaru obliczana jest z równania:

%

100

%

s

g

X

X

X

∆

=

δ

.

(42)

b)

Pomiar pośredni:

Wartość wielkości mierzonej pośrednio Y jest funk-
cją k-wielkości mierzonych bezpośrednio

)

,.....,

(

1

k

X

X

f

Y

=

, a pomiar każdej z wielkości X

powtarzamy n-krotnie:

kn

k

n

X

X

X

X

.....

.....

.....

.....

.....

1

1

11

-

Obliczamy wartości średnie X

1s

÷

X

ks

wielkości

mierzonych bezpośrednio z zależności (14);

-

Wartość średnia wielkości mierzonej pośrednio
jest równa:

)

,....,

(

1

ks

s

s

X

X

f

Y

=

(43)

Należy obliczyć błędy średnie przypadkowe po-
szczególnych wielkości

∆

sp

X

is

posługując się za-

leżnością (18);

-

Błąd średni przypadkowy wartości średniej
wielkości Y wyznacza się z zależności (34),
tzn.:

∑

=

∆













∂

∂

=

∆

k

i

is

sp

i

s

sp

X

X

Y

Y

1

2

2

)

(

-

Błąd średni systematyczny wielkości Y oblicza
się z zależności:

















=

∆













∂

∂

+

∆













∂

∂

≥

∆













∂

∂

=

∆

∑

=

2

)

(

)

(

82

,

0

3

)

(

2

2

2

2

2

1

2

1

1

2

2

k

X

X

Y

X

X

Y

k

X

X

Y

Y

ss

ss

k

i

i

ss

i

ss

(44)

gdzie:

3

i

gs

i

ss

X

X

∆

=

∆

(zależność (21)) ;

-

Błąd średni wypadkowy pomiaru wyznacza się
następująco:

2

2

)

(

)

(

Y

Y

Y

ss

s

sp

s

∆

+

∆

=

∆

.

(45)

-

Błąd graniczny pomiaru oblicza się ze wzoru

Y

Y

s

g

∆

⋅

=

∆

3

.

(46)

-

Wynik pomiaru zapisywany jest w postaci (41)
a dokładność (42).

2.6. Zasady podawania wyników oblicze

ń

Każdy pomiar powinien być tak zorganizowany,

aby obliczeń niezbędnych do otrzymania wyniku
końcowego było jak najmniej. Należy przy tym
pamiętać, że obliczeń nie należy dokonywać nigdy z
dokładnością większą niż pozwalają na to posiadane
dane wyjściowe.

Przy dodawaniu lub odejmowaniu uwzględniamy

tylko te miejsca składników, które występują przy
wszystkich liczbach, np.:

Ź

le

Dobrze

271,2

14,51

+ 0,125

285,835

271,2
14,5
+ 0,1
285,8

W celu zmniejszenia pracochłonności przy mnoże-
niu lub dzieleniu wskazane jest, aby czynniki miały
te same ilości cyfr znaczących, np.:

Ź

le

Dobrze

217,63 V x 0,234 A

lub

217 V x 0,23456 A

217,6 V x 0,2346 A

8

Wyniki przeprowadzanych obliczeń należy po-

nadto zaokrąglić posługując się następującymi regu-
łami:
1)

jeżeli pierwsza (licząc od lewej strony) z odrzu-
canych cyfr jest mniejsza od 5, to ostatniej po-
zostawianej cyfry nie zmienia się, np.:

49,64

≈

49,6

2)

jeżeli pierwsza (licząc od lewej strony) z odrzu-
canych cyfr jest większa od 5, to ostatnią pozo-
stawiana cyfrę powiększa się o jeden, np.:

49,66

≈

49,7

3)

jeżeli pierwsza (licząc od lewej strony) z odrzu-
canych cyfr jest równa 5, ale następuje po niej
co najmniej jeszcze jedna cyfra inna niż 0, to
ostatnią pozostawioną cyfrę powiększa się o je-
den, np.:

49,6512

≈

49,7

49,6501

≈

49,7

4)

jeżeli pierwsza (licząc od lewej strony) z odrzu-
canych cyfr jest równa 5, ale nie następuje po
niej żadna inna cyfra niż zero, to ostatnią pozo-
stawioną cyfrę powiększa się o jeden jedynie w
tym przypadku, jeżeli jest to cyfra nieparzysta
(zero traktuje się jak cyfrę parzystą), np.:

49,65

≈

49,6

49,75

≈

49,8

49,85

≈

49,8

Przy tworzeniu ostatecznej postaci wyniku po-

miaru wygodnie jest posłużyć się dwiema regułami
– regułą podawania błędu i regułą podawania odpo-
wiedzi [5].

Reguła podawania bł

ę

du

Ponieważ błąd jest miarą niewiarygodności ostatniej
cyfry, bądź dwóch ostatnich cyfr znaczących warto-
ś

ci liczbowej, nie określa się go zwykle z większą

dokładnością aniżeli jedną cyfrą znaczącą. Błąd
podaje się za pomocą co najwyżej dwóch cyfr zna-
czących:

•

jeśli ma być użyty do dalszych obliczeń
(zmniejsza to niedokładności wprowadzane
podczas zaokrąglania a końcowy wynik powi-
nien być i tak zaokrąglony aby usunąć tę dodat-
kową i nieznaczącą cyfrę),

•

jeśli pierwszą cyfra znaczącą jest 1 lub 2 (za-
okrąglenie błędu np.

∆

= 0,14 do wartości 0,1

prowadziłoby do 40% zmniejszenia jego warto-
ś

ci).

Reguła podawania odpowiedzi

Ostatnia cyfra znacząca w każdym wyniku końco-
wym powinna być tego samego rzędu (stać na tym
samym miejscu dziesiętnym) co błąd. Np. wynik
92,81 określony z błędem 0,3 powinien być zaokrą-
glony do:

92,8

±

0,3

Jeśli błąd jest równy 3, to ten sam wyniki należy
podać jako:

93

±

3

Jeśli natomiast błąd wynosi 30, to odpowiedź po-
winna brzmieć:

90

±

30

Całkowicie niedorzeczne jest podawanie wyniku w
postaci np.:

9,81

±

0,0356789

2.7. Zasady tworzenia wykresów

Wykresy sporządzanych zależności powinny być

wykonane estetycznie, ręcznie przy pomocy krzywi-
ków lub w postaci wydruków na standardowych
rozmiarach papierów. Wykresy wykonane ręcznie
muszą być nanoszone na papier milimetrowy a wy-
druki komputerowe można robić na papierze gład-
kim.

Każdy wykres powinien być zaopatrzony w opis

zależności funkcyjnej oraz informację w jakich
warunkach był „zdejmowany”. Osie wykresów po-
winny być oznaczone, tzn. powinny zawierać infor-
mację jakie wielkość są na nich odłożone oraz w
jakich jednostkach są wykreślone ich wartości. Jeże-
li na danym wykresie naniesiono kilka krzywych to
należy je wykreślić różnymi kolorami lub przy po-
mocy symboli np.

•

, o, x,

∗

, itp. Wykres taki zawsze

powinien być jednoznaczny – opis poszczególnych
krzywych należy zawrzeć pod rysunkiem lub w
legendzie – rys. 3.

Ogólnie dostępny papier milimetrowy reprezen-

tuje tzw. siatkę liniowo-liniową. Oprócz siatki li-
niowej, w celu uwypuklenia charakterystycznych
zmian interesującej nas zależności, stosuje się jesz-
cze siatki logarytmiczne: liniowo-logarytmiczną,
logarytmiczno-liniową i logarytmiczno-logarytmi-
czną – rys. 4. Siatka liniowo-logarytmiczna znajduje
zastosowanie gdy zakres liczbowy wartości osi
rzędnych (oś y) jest znaczny, tzn. poszczególne
wartości y

i

różnią się między sobą o rzędy wielkości.

Pozwala ona ponadto na sprawdzenie istnienia mię-
dzy dwiema wielkościami zależności typu y=Ae

ax

,

gdzie A, a – stałe, gdyż linearyzuje jej wykres. Po-
dobnie, gdy wartości osi odciętych x charakteryzują
się dużym zakresem zmian, wykorzystywana jest

Rys. 3. Przykład wykresu.

9

siatka logarytmiczno-liniowa. Dodatkowo pozwala
na linearyzację zależności typu y=A+alnx, gdzie A, a
– stałe. Siatkę logarytmiczno-logarytmiczną wyko-
rzystuje się natomiast w sytuacji, gdy wartości na
obu osiach charakteryzują się dużymi zakresami
zmian oraz do sprawdzania zależności typu y=Ax

a

,

gdzie A, a – stałe. Pewną odmianą skali logaryt-
micznej dla osi rzędnych jest skala decybelowa,
służąca do wyrażania stosunku wartości interesują-
cej nas wielkości np. U do pewnej wielkości odnie-
sienia U

0

. Wartość U/U

0

wyrażona w skali decybe-

lowej wynosi:

0

0

lg

20

]

[

U

U

dB

U

U

=

,

(47)

gdzie lg jest oznaczeniem logarytm dziesiętnego.
Wykorzystuje się ją do zobrazowania dużego zakre-
su zmian pewnych wielkości stosunkowych, np.
wzmocnienia.

W przypadku braku dostępu do siatki logaryt-

micznej wykres można również wykonać na zwy-
kłym papierze milimetrowym stosując odpowiednie
skalowanie.
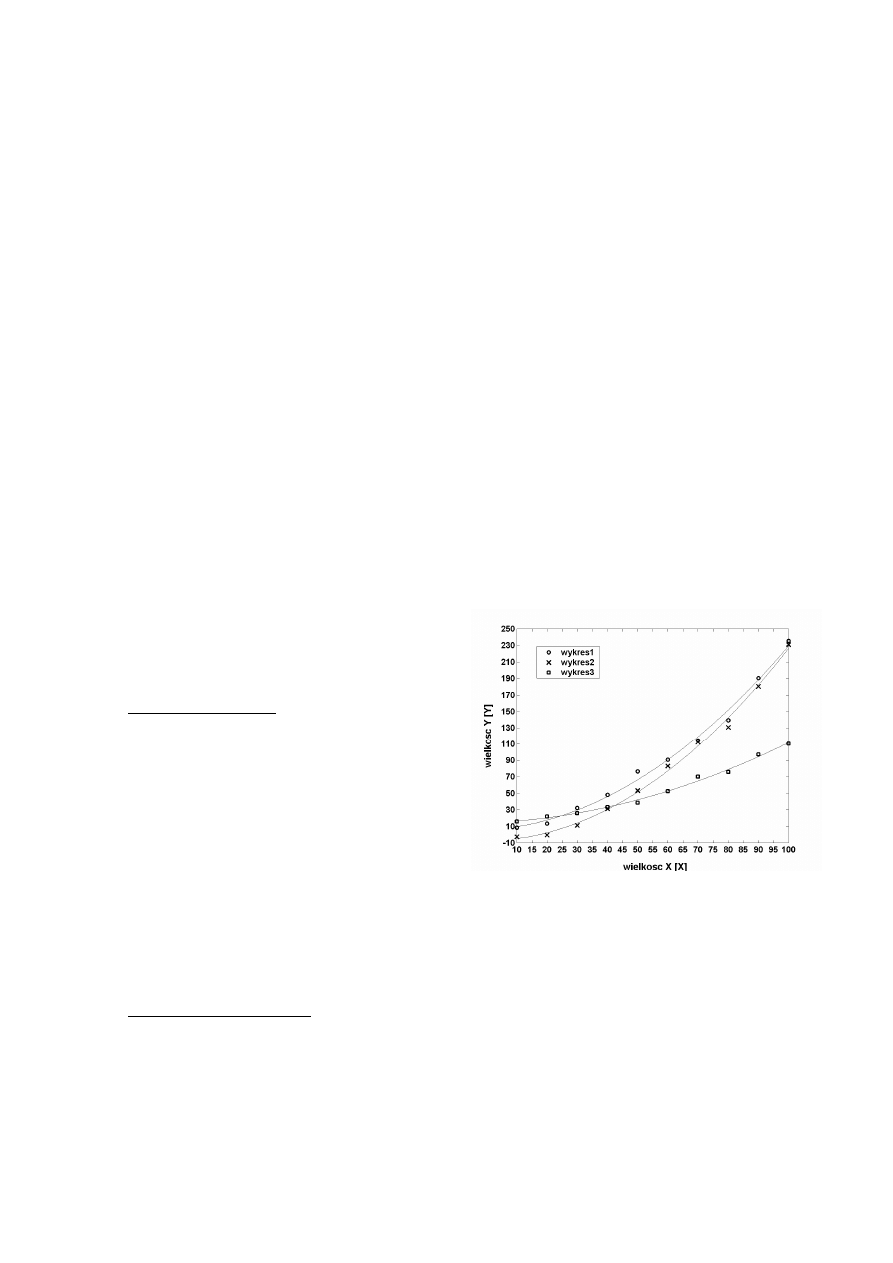
Przykład. W tabeli 6 w wierszach 1-3 przedstawiono
wyniki pomiaru przebiegu wzmocnienia pewnego
wzmacniacza w funkcji częstotliwości. Wykres
sporządzony na podstawie wartości zawartych w
tabeli 6 i przedstawiony na rys. 5 w skali liniowej
jest całkowicie nieczytelny dla małych częstotliwo-
ś

ci. Warto zastanowić się chwilę nad wartościami f.

Obejmują one zakres od 1Hz do 2MHz czyli ponad
6 dekad. Dekadę tworzy przedział, którego górna
granica jest 10 razy większa od dolnej. Pierwsza

dekada obejmuje więc zakres (0,10)Hz, druga
(10,100)Hz, trzecia (100,1000)Hz itd. Długości tych
przedziałów w skali liniowej rosną. Zastosowanie
skali logarytmicznej (np. logarytmu przy podstawie
10 z wartości częstotliwości) sprawia, że na rysunku
będą one miały tę samą długość. Przypuśćmy, że na
wykonanie osi dla f mamy do dyspozycji 21cm.
Rezerwując na każdą dekadę w skali logarytmicznej
po 3cm uzyskamy długość odcinka odpowiadające-
go wszystkim 6 dekadom równą 6

⋅

3cm=18cm. Po-

szczególnym granicom przedziałów będą więc od-
powiadały następujące wartości w centymetrach:

10

0

Hz

→

0cm

10

1

Hz

→

3cm

10

2

Hz

→

6cm

10

3

Hz

→

9cm

itd.

Zależność przeskalowująca jest oczywista: warto-
ś

ciom częstotliwości wyrażonym w hercach należy

przypisać następujące odległości na osi wyrażone w
centymetrach:

f

’[cm]={log

10

[f[Hz]]}

⋅

3[cm].

Wiersz 4 tabeli 6 zawiera obliczone wartości f’[cm]
a odpowiedni wykres w uzyskanej skali logaryt-
miczno-liniowej przedstawia rys. 6. Można na nim
zaobserwować pasmowy charakter wzmocnienia
wzmacniacza z dwoma podbiciami w zakresie ni-
skich i wysokich częstotliwości.

W celu wykorzystania pełnej powierzchni rysun-

ku niejednokrotnie konieczne jest przesuwanie po-
czątku układu współrzędnych.
Przykład. W tabeli 7 w wierszach 1-3 przedstawiono
wyniki charakterystyki przetwarzania pewnego
wzmacniacza.

Tabela 6.

Wyniki pomiarów wzmocnienia K pewnego wzmacniacza w funkcji częstotliwości f.

Lp

-

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

f

Hz

1

1.5

2

4

8

12 20 40

500

1.5

⋅

10

3

1.5

⋅

10

4

6

⋅

10

3

10

5

2

⋅

10

5

4

⋅

10

5

6

⋅

10

5

9

⋅

10

5

1.5

⋅

10

6

2

⋅

10

6

K

V/V

0

2

5

9

11 12 11 10

10

10

10

11

15

20

15

9

5

2

0

f’

cm

0

0,5 0,9 1,8 2,7 3,2 3,9 4,8

8,1

9,5

12,5

14,3

15,9

16,8

17,3

17,9

18,5

18,9

Rys. 5. Przykład źle dobranej skali dla osi częstotliwości.

Rys. 4. Rodzaje siatek: a) liniowa, b) liniowo-

logarytmiczna, c) logarytmiczno-liniowa,

d) logarytmiczno-logarytmiczna.

15,0

10

Tabela 7.

Przykładowa charakterystyka przetwarza-

nia.

Lp.

-

1

2

3

4

5

U

we

mV

100

105

110

115

120

U

wy

mV

201

213

221

230

243

U’

we

mV

0

4

8

12

16

U’

wy

mV

0,5

6,5

10,5

15,0

21,5

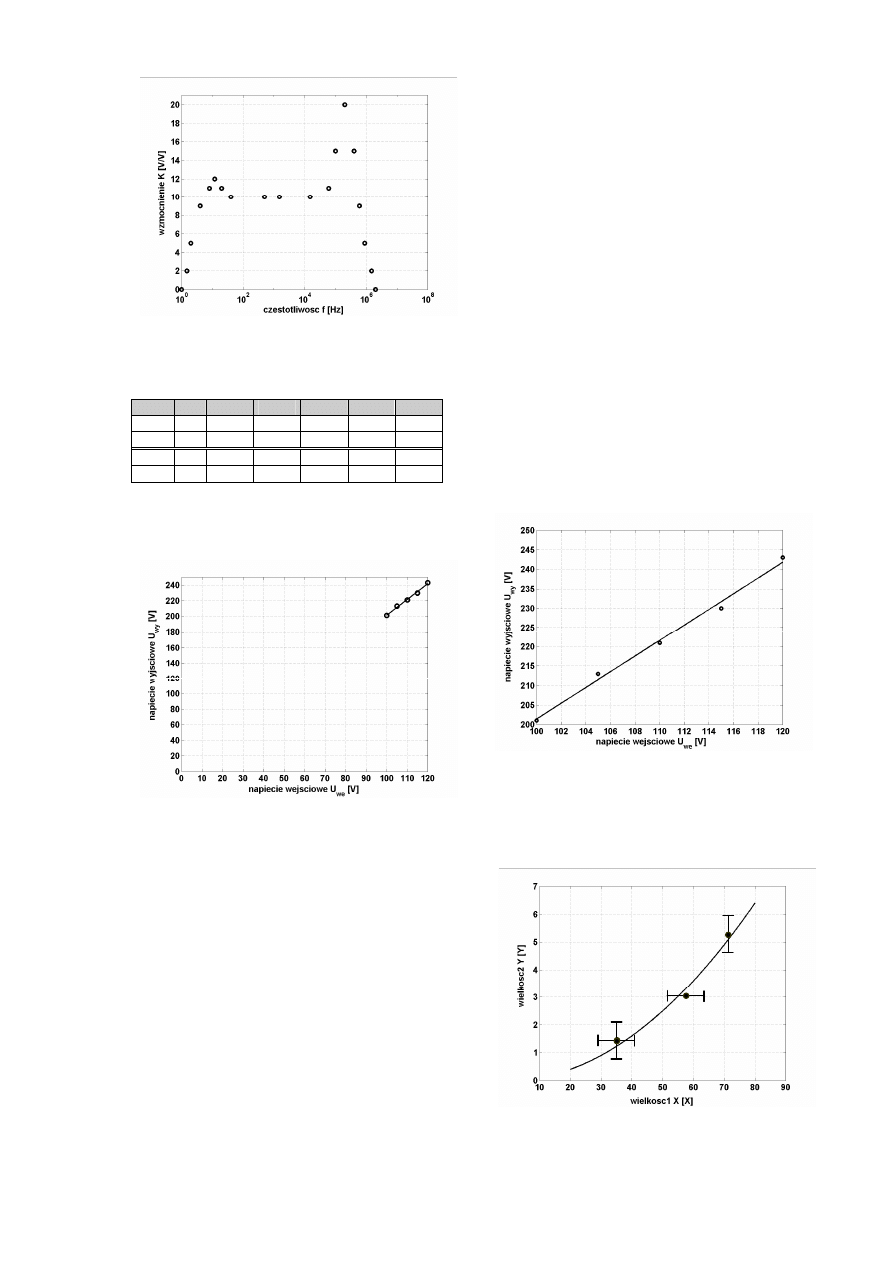
Podobnie jak poprzednio, wykres sporządzony na
ich podstawie – rys. 7 jest nieczytelny i wymaga
przesunięcia początku układu współrzędnych.

Przypuśćmy, że mamy do dyspozycji 18cm dla osi x
i 25cm dla osi y. Należy zastosować takie zależności
przeskalowujące, aby po pierwsze – wielokrotność
działki podstawowej papieru milimetrowego np.
1cm, 2cm, 3cm itd. odpowiadała 1, 2, 5, 10, 20, 50
itd. jednostkom mierzonej wielkości (należy to za-
pewnić zawsze, niezależnie od konieczności prze-
suwania początku układu współrzędnych) i po dru-
gie – aby w pełni wykorzystać powierzchnię wykre-
su. Rozważmy oś x. Chcemy, aby długości ok. 18cm
odpowiadał przedział o szerokości

120mV-100mV=20mV.

Przy skalach bazujących na jednostce papieru mili-
metrowego np. 1cm/1mV i 1cm/2mV uzyskujemy
wartości

20mV

⋅

(1cm/1mV)=20cm

oraz 20mV

⋅

(1cm/2mV)=10cm,

odpowiadające kolejno – przekroczeniu i znacznemu
niewypełnieniu dostępnego zakresu 18cm. Przy

zastosowaniu skali S

x

=4cm/5mV bazującej na wie-

lokrotności działki podstawowej papieru milimetro-
wego uzyskujemy wartość

20mV

⋅

(4cm/5mV)=16cm,

co już można uważać za rozsądne wypełnienie do-
stępnego zakresu. Zależność przeskalowująca będzie
więc miała postać:

U’

we

[cm]=

=(U

we

-U

wemin

)

⋅

S

x

=(U

we

-100mV)

⋅

(4cm/5mV).

Podobnie postępując można dla osi y wyprowadzić
zależność:

U’

wy

[cm]=(U

wy

-U

wymin

)

⋅

S

y

,

W której S

y

najwygodniej wyznaczyc tak, aby zakre-

sowi 25cm odpowiadał przedział (200,250)mV,
czyli przedział o szerokości 50mV:

S

y

=1cm/2mV,

gdyż 50mV

⋅

S

y

=25cm. Ostatecznie więc:

U’

wy

[cm]=(U

wy

-200mV)

⋅

(1cm/2mV).

Wyznaczone wartości U’

we

[cm] i U’

wy

[cm] zawiera

w wierszach 4-5 tabela 7, a sporządzony na ich pod-
stawie wykres przedstawia rys. 8.

Niekiedy należy na wykresie zaznaczyć stopień

dokładności realizowanych pomiarów. Używa się
wówczas oznaczeń przedstawionych na rys. 9.

Rys. 7. Przykład złego rozplanowania powierzchni

rysunku.

Rys. 8. Przykład dobrego rozplanowania powierzchni

rysunku.

Rys. 6. Przykład dobrze dobranej skali dla osi częstotliwości.

Rys. 9. Przykłady oznaczania na wykresach dokład-

ności pomiarów.

dokładno

ść

wielko

ś

ci Y

dokładno

ść

wielko

ś

ci X

dokładno

ść

wielko

ś

ci X i Y

11

W większości przypadków należy również jako

zasadę przyjąc fakt, iż poszczególnych punktów
wykresu nie należy łączyć krzywą łamaną. Można
tak postapić jedynie wówczas, gdy przedstawiane
zależności mają znaczenie jedynie formalne. W
przypadku wielkości fizycznych należy dokonać
przybliżenia

dyskretnych

wyników

pomiarów

wykonując

tzw.

aproksymację.

Zadaniem

aproksymacji

zależności

między

dwiema

wielkościami X i Y jest szacowanie jej przebiegu na
podstawie przeprowadzonych pomiarów. Można
tego dokonać w sposób graficzny za pomocą
krzywików

i

linijki,

prowadząc

krzywą

aproksymującą tak, aby przechodziła ona przez jak
największą liczbę punktów określonych empirycznie
lub blisko nich. Rozłożenie punktów względem
krzywej powinno być, według oceny “na oko”,
symetryczne z zachowaniem, w miarę możliwości,
jednakowej liczby punktów po jej obu stronach.

Znacznie dokładniejszą metodą aproksymacji

jest metoda analityczna zwana metodą naj-
mniejszych kwadratów lub metodą regresji. W
najbardziej elementarnym ujęciu jako funkcję
aproksymująca przyjmuje się wielomian n-tego
rzędu:

n

n

X

a

X

a

X

a

a

X

f

Y

+

+

+

+

=

=

...

)

(

2

2

1

0

, (48)

którego współczynniki a

0

, a

1

, ..., a

n

wyznacza się na

podstawie wyników pomiarów. Stopień wielomianu
przyjmowany jest z reguły na podstawie pewnej
wiedzy a priori o badanej zależności, tzn. należy
założyć, że jest ona liniowa (n=1), kwadratowa
(n=2), sześcienna (n=3) itd.
Przy braku tej wiedzy rząd wielomianu można do-
bierać eksperymentalnie, pamiętając jednak, że jego
wzrost prowadzi, co prawda, do zmniejszenia błędu
dopasowania krzywej aproksymującej do punktów
empirycznych, ale kosztem pojawienia się między
nimi niepożądanych oscylacji.
Zasada wyznaczania funkcji aproksymującej jest
następująca.
Przypuśćmy, że chodzi o wyznaczenie często wystę-
pującej w praktyce zależności liniowej dla N punk-
tów pomiarowych. Poszukujemy a

0

i a

1

w formule:

X

a

a

Y

1

0

+

=

.

(49)

Przy zakładanej liniowości danemu punktowi po-
miarowemu x

i

powinna odpowiadać wartość

y’

i

= a

0

+a

1

x

i

. Z pomiarów znamy jednak „błędne” y

i

,

więc różnica

∆

i

= y

i

-(a

0

+a

1

x

i

) jest błędem i-tego wy-

niku y

i

. Tworząc sumę kwadratów wszystkich błę-

dów:

(

)

[

]

∑

∑

=

=

+

−

=

∆

N

i

i

i

N

i

i

x

a

a

y

1

2

1

0

1

2

,

(50)

możemy znaleźć takie a

0

i a

1

, dla których powyższa

suma osiąga minimum (stąd uzasadnienie nazwy –
metoda najmniejszych kwadratów). Badanie mini-
mum jest zadaniem trywialnym i polega na wyzna-
czeniu pochodnych względem a

0

i a

1

i przyrównaniu

ich do zera [5]. Z układu dwu równań wyznacza się
wówczas wartości a

0

i a

1

:

( )( )

( )

,

1

0

2

2

1

N

x

a

N

y

a

x

x

N

y

x

y

x

N

a

i

i

i

i

i

i

i

i

∑

∑

∑

∑

∑

∑

∑

−

=

−

−

=

(51)

w których operacje sumowania odbywają się wzglę-
dem indeksu i. Otrzymane wartości dają najlepsze
przybliżenie współczynników poszukiwanej prostej
oparte na wynikach pomiarów w sensie średniokwa-
dratowym. Organizacja powyższych obliczeń po-
winna być w sprawozdaniu zobrazowana tabelą
zestawiającą kolejno wartości x

i

, y

i

, x

i

y

i

, x

i

2

potrzeb-

ne do końcowych wzorów.
Przedstawioną metodę łatwo uogólnić na przypadek
wielomianu dowolnego stopnia lub dowolnej funkcji
y

=f(x) zależnej od nieznanych parametrów a

0

, a

1

, ...,

jednakże powstałe równania liniowe mogą być wte-
dy trudne lub wręcz niemożliwe do rozwiązania.

Zagadnienia aproksymacji nie należy mylić z in-

ną metodą znajdowania zależności funkcyjnej mię-
dzy danymi uzyskanymi z pomiaru, zwaną interpo-
lacją. Polega ona na wyznaczeniu krzywej, która jest
dopasowana z zerowym błędem do wyników pomia-
rów (przechodzi przez wszystkie punkty empirycz-
ne). W zagadnieniach interpolacji wykorzystuje się
m. in. metody funkcji sklejanych (ang. splines).

3.

O

PRACOWANIE WYNIKÓW

POMIARÓW WSPOMAGANE KOMPUTEREM

–

WPROWADZENIE DO

MATLABA

Współczesne mikrokomputery oraz istniejące

oprogramowanie stanowią niezwykle atrakcyjne
narzędzie w procesie opracowania wyników ekspe-
rymentu. Zwalniają użytkownika z wykonywania –
wielu żmudnych i uciążliwych obliczeń, umożliwia-
ją praktycznie dowolne ich modyfikacje oraz szyb-
kie i w dowolnej formie zobrazowanie wyników
końcowych. Często problemem staje się nie sposób
wykonania obliczeń (korzysta się z gotowych proce-
dur), ale samo określenie celu naszych poczynań.
Dostępność kolorowych drukarek i ploterów spra-
wia, że opracowane sprawozdania mogą być zaopa-
trzone w wysoce estetyczne i czytelne wykresy mie-
rzonych wielkości.

W procesie tworzenia sprawozdania można sko-

rzystać z dowolnego języka programowania ogólne-
go przeznaczenia tworząc własne procedury prze-
twarzania i zobrazowania wyników pomiarów, lub z
jednego z programów specjalistycznych, zaopatrzo-
nego w użyteczne dla nas biblioteki procedur. Jed-
nym z takich programów jest pakiet MATLAB.
Stanowi on rozbudowane środowisko programi-
styczne, bazujące na bogatym zestawie tzw. „tool-
boxów”, czyli bibliotek procedur mających zastoso-
wanie w wielu dziedzinach np. w ekonometrii, sie-
ciach neuronowych, cyfrowym przetwarzaniu sygna-
łów, statystyce, optymalizacji itp. Jest to środowisko
otwarte – umożliwia tworzenie również własnych
procedur. Zastosowanie MATLABA w opracowaniu

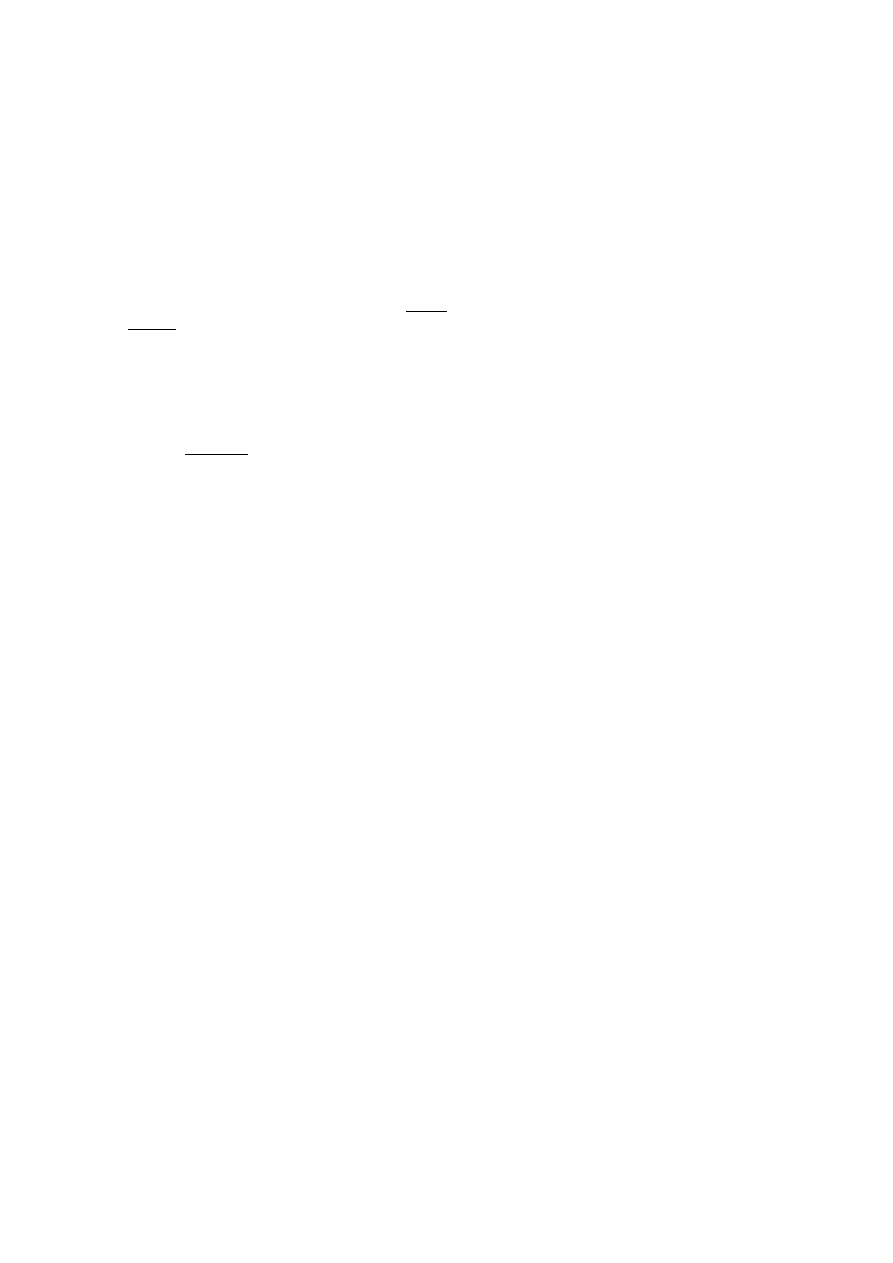
12

wyników pomiarów jest niezwykle wygodne ze
względu na:

•

łatwość operowania wprowadzonymi wynikami
pomiarów,

•

istnienie użytecznych procedur graficznych i
obliczeniowych,

•

możliwość przeprowadzania aproksymacji i
interpolacji,

•

możliwość składowania wyników obliczeń w
postaci plików tekstowych rozpoznawanych
przez inne programy.

Praca z MATLABEM może odbywać się w dwu

trybach: bezpośrednim i pośrednim. W trybie bezpo-
ś

rednim użytkownik ma do dyspozycji okno „Ma-

tlab Command Window”, w którym wszystkie ope-
racje wpisane po znaku zachęty

>>

i potwierdzone

klawiszem Enter wykonywane są natychmiastowo z
przypisaniem wyniku do zmiennej

ans

, np.:

>>2+2

↵

Enter

ans=4

W trybie pośrednim, w zewnętrznym edytorze tekstu
(można i zaleca się wykorzystywać edytor wbudo-
wany), tworzy się plik tekstowy zwany skryptem
MATLABA. W pliku tym, zapamiętanym pod okre-
ś

loną nazwą i w miejscu wymaganym przez zadekla-

rowaną w „Matlab Command Window” ścieżkę
dostępu, wpisuje się linie programu, które będą
wykonane w kolejności wprowadzania po wywoła-
niu w oknie „Matlab Command Window” nazwy
napisanego skryptu. Wykorzystanie trybu pośred-
niego jest bardziej efektywne, gdyż umożliwia edy-
cję i ewentualne poprawki np. błędnie wprowadzo-
nych wyników pomiarów.
W ogólności, dane w MATLABIE reprezentowane
są za pomocą wektorów oraz dwu- lub trójwymia-
rowych tablic zwanych macierzami. W procesie
opracowania wyników pomiarów pierwszym kro-
kiem jest wprowadzenie wartości uzyskanych z
eksperymentu jako elementów wektorów (lub ma-
cierzy). Następnie wykonuje się niezbędne oblicze-
nia z użyciem dostępnych procedur, zobrazowuje
wyniki, przeprowadza się (jeżeli jest to wymagane)
aproksymację, zapamiętuje się wyniki lub dokonuje
się ich wydruku. Wykonanie powyższych kroków
wymaga znajomości posługiwania się funkcjami i
znakami specjalnymi MATLABA, których skrócony
wykaz i opis znajduje się poniżej.

3.1. Znaki specjalne pomocne w procesie wpro-

wadzania wyników pomiarów

[ ]

nawiasy kwadratowe: tworzenie wektorów

(ciągów) danych

Nawiasy kwadratowe są używane do tworzenia wektorów.
Na przykład A=[11 12 13 21 22 23] jest wektorem (cią-
giem) składającym się z sześciu wyników pomiarów.
Elementy wektora oddzielane są spacjami lub przecin-
kami. Następujące zapisy wektora o trzech elementach są
równoważne: [1 1.25 sqrt(9)] lub [1, 1.25 , sqrt(9)].
Wewnątrz nawiasów kwadratowych mogą wystąpić inne
wektory zawierające dane. Na przykład [A B] jest wekto-
rem, który powstał z połączenia wektorów A i B. [ ] jest

wektorem zerowym (o wymiarze zero lub inaczej wekto-
rem pustym).

( )

nawiasy okrągłe

Określają kolejność wykonywania działań arytmetycznych
w zwyczajowo przyjęty sposób. Używane są także pod-
czas wywołania funkcji - otaczają listę argumentów funk-
cji. Służą do oznaczania indeksów wektorów danych, przy
czym przyjmuje się, że indeksy te rozpoczynają się od
jedności: X(1) jest pierwszym elementem wektora X, X(3)
jest trzecim elementem wektora X itd. Jeśli dowolny z
indeksów jest mniejszy od jedności lub większy od roz-
miaru wektora, to wystąpi błąd. Zapis: Y=X([1 2 3]) ozna-
cza wektor składający się z pierwszych trzech elementów
wektora X.

,

przecinek

Oddziela indeksy wektorów, argumenty funkcji oraz
wyrażenia zapisane w jednym wierszu. W tym ostatnim
przypadku można go zastąpić średnikiem, jeżeli chcemy
uniknąć wyświetlania wyników tych wyrażeń.

;

średnik

Umieszczony na końcu wyrażenia blokuje wyświetlenie
wyników tego wyrażenia na ekranie.

eN

zapis mnożnika 10

N

Powyższy znak umożliwia zapis zmiennoprzecinkowy, np.
liczba 0.00025 jest równoważna liczbie 2.5e-3.

:

dwukropek

Służy do konstrukcji wektorów o liniowo rosnących lub
malejących elementach. Na przykład J:K jest rów-
noważne wyrażeniu [J, J+1, .., K] (jeżeli J>K, to J:K jest
wektorem pustym). J:I:K jest równoważne wyrażeniu
[J,J+I, J+2*I, ..., K] (jeżeli I>0 i jednocześnie J>K lub
jeżeli I<0 i jednocześnie J<K, to J:I:K jest wektorem
pustym).

3.2. Znaki specjalne i funkcje pomocne w prze-

twarzania wprowadzonych danych

.

kropka dziesiętna

Kropka dziesiętna służy do oddzielania części ułamkowej
liczby dziesiętnej: 314/100, 3.14 oraz .314e1 oznaczają
jedną i tę samą liczbę. Kropka umieszczona przed takimi
operatorami multiplikatywnymi jak: *, ^, / oznacza dzia-
łania na kolejnych elementach wektorów. Na przykład:
C=A .* B jest wektorem, którego elementy zostały wy-
znaczone z zależności C(i)=A(i)*B(i). Brak kropki w
powyższym wyrażeniu tzn. zapis C=A * B oznacza zupeł-
nie inny rodzaj działania wykonany na wektorach A i B.
Dwie lub więcej kropek na końcu linii oznacza, że na-
stępną linię należy traktować jako linie kontynuacji.

‘

cudzysłów

Jest używany do zaznaczania wyrażenia tekstowego np.
'To jest podpis pod rysunkiem', występującego jako ar-
gument wywoływanej funkcji. Jeżeli wewnątrz tego napi-
su miałby występować znak cudzysłowu, to należy go
użyć dwa razy.

+

dodawanie

Wyrażenie X+Y oznacza sumę wektorów X i Y. Wektory
X i Y muszą składać się z tej samej liczby elementów.
Wyrażenie X+a, gdzie X jest wektorem, a-skalarem, daje

13

w wyniku wektor otrzymany przez dodanie a do każdego
elementu X.

-

odejmowanie

Wyrażenie X-Y oznacza różnicę wektorów X i Y. Wekto-
ry X i Y muszą składać się z tej samej liczby elementów.
Wyrażenie X-a, gdzie X jest wektorem, a-skalarem, daje
w wyniku wektor otrzymaną przez odjęcie a od każdego
elementu X.

*

mnożenie

Wyrażenie a*X lub X*a, gdzie X jest wektorem, a-
skalarem, daje w wyniku wektor otrzymany przez prze-
mnożenie każdego elementu wektora X przez skalar a.
Mnożenie elementu X(i) wektora X przez element Y(i)
wektora Y otrzymuje się poprzedzając znak * kropką
dziesiętną: X.*Y. Jest to mnożenie typu element przez
element. Wektory X i Y muszą wówczas mieć takie same
wymiary (chyba, że jedna z nich jest skalarem).

^

potęgowanie

Zapis y=x^a, gdzie x, y, a są skalarami, jest zapisem
podnoszenia x do potęgi a. Wyrażenie Y=X. ^a oznacza
podnoszenie każdego elementu wektora X do potęgi a, a
Y=X.^Z oznacza potęgowanie typu element przez ele-
ment. Wektory X i Z muszą w takim przypadku mieć takie
same wymiary (chyba że jedna z nich jest skalarem).

abs

wartość bezwzględna

abs(X) - wartość bezwzględna elementów wektora X.
Jeżeli X zawiera elementy zespolone, abs(X) zwraca mo-
duły (pierwiastek z sumy kwadratów części rzeczywistej i
urojonej) kolejnych jego elementów

sqrt

pierwiastek kwadratowy

sqrt(X) wyznacza pierwiastek kwadratowy elementów
wektora X. Jeśli którykolwiek z elementów X jest ujemny,
to wynik będzie zespolony.

mean

wartość średnia

Gdy X jest wektorem, mean(X) jest średnią arytmetyczną
jego elementów.

std

odchylenie standardowe

Gdy X jest wektorem, std(X) jest odchyleniem standar-
dowym jego elementów.

log10

logarytm przy podstawie 10

Dla wektorów log10(X) jest logarytmem przy podstawie
10 z każdego z elementów.

3.3. Funkcje i polecenia pomocne w zobrazowa-

niu wyników

plot

wykreśl

Służy do tworzenia wykresów. Aby utworzyć wykres,
którego kolejne punkty mają współrzędne określone przez
wektory X i Y, należy użyć instrukcji plot(X,Y). Sposo-
bem na wyświetlanie kilku wykresów przy jednym użyciu
funkcji plot jest użycie kilku par argumentów:
plot(X1,Y1,X2,Y2,...). Do każdej pary argumentów X, Y
można dodać opcjonalny trzeci argument - ciąg znaków
określający rodzaj i kolor linii wykresu i markerów.
Rodzaje linii: - ciągła, -- przerywana, . kropkowa, -. linia

typu „kreska - kropka".

Rodzaje markerów (sposobów oznaczania punktów

wykresu określonych przez wektory X i Y):

. (kropka), + znak plus, * gwiazdka, x krzyżyk

(litera 'x'), o kółko (litera 'o').

Kolory: r czerwony (red), g zielony (green), b niebieski

(blue), w biały (white), i kolor tła (invisible),
cl...c15 kolor o podanym numerze (z palety 16
kolorów).

Ponadto dopuszczalne są następujące warianty instrukcji
plot:
plot(Y) - wykres wektora Y według indeksów jego ele-
mentów,
plot(Y) - gdzie Y oznacza wektor zawierający wartości
zespolone,

jest

równoważna

instrukcji

plot(real(Y),imag(Y)) (w przypadku użycia argumentów
zespolonych w innych postaciach instrukcji plot, część
urojona zostanie zignorowana).
Przykłady: plot(x,y,'b--') - wykres będzie wyświetlony
linią przerywaną w kolorze niebieskim,
plot(x,y,xl,yl,'-',x2,y2,'--') - trzy wykresy, dla drugiego i
trzeciego określono rodzaje linii.

subplot

podwykres

subplot(mnp) określa podział ekranu. Ekran graficzny
zostaje podzielony na m x n części i w każdej z tych
części można umieścić osobny wykres. Argumentem mnp
instrukcji jest liczba 3-cyfrowa, której pierwsza cyfra m
określa sposób podziału w pionie (liczbę rzędów wykre-
sów), druga cyfra n - sposób podziału w poziomie (liczbę
kolumn wykresów), a trzecia cyfra p określa część, w
której pojawi się następny wykres. Na przykład, instrukcja
subplot(223) umożliwi podział ekranu w pionie i pozio-
mie na dwie części (łącznie na cztery pola wykresów) i
wybranie lewego dolnego pola do umieszczenia tam ko-
lejnego wykresu

semilogx

wykreśl z logarytmiczną osią x

Utworzenie wykresu z logarytmiczną (o podstawie 10)
skalą na osi x i liniową skalą na osi y. Składnia i para-
metry - patrz opis instrukcji plot.

semilogx

wykreśl z logarytmiczną osią y

Utworzenie wykresu z logarytmiczną (o podstawie 10)
skalą na osi y i liniową skalą na osi x. Składnia i para-
metry - patrz opis instrukcji plot.

loglog

wykreśl w skali log-log

loglog(...) działa tak samo jak plot(...), z tym wyjątkiem,
ż

e na obu osiach są stosowane skale logarytmiczne.

xlabel

oznaczenie osi x

xlabel('tekst') umieszcza tekst podany jako argument na
aktualnym wykresie pod osią poziomą.

ylabel

oznaczenie osi y

ylabel('tekst') umieszcza tekst podany jako argument na
aktualnym wykresie przy osi pionowej.

grid

wyświetl siatkę

Powyższe polecenie wyświetla linie siatki na aktualnym
rysunku.

hold

zatrzymaj aktualny wykres

hold on włącza tryb zatrzymywania rysunków, hold off
powraca do normalnego trybu, gdzie następny rysunek
wymazuje poprzedni. Samo hold przełącza tryb zatrzy-
mywania rysunku. Następne wywołania funkcji plot będą
uzupełniały (o ile są wykonywane w stanie on przełączni-

14

ka hold) aktualny rysunek o kolejne wykresy i wykorzy-
stywały istniejące zakresy wartości na osiach współrzęd-
nych.

legend

wprowadzenie legendy do wykresu

legend(string1,string2,...) tworzy na aktualnym wykresie
opis siatki w postaci legendy wykorzystując jako oznacze-
nia wyspecyfikowane łańcuchy znaków ( tzw. stringi). Np.
legend(‘wykres1’,’wykres2’,’wykres3’).

3.4. Funkcje pomocne w aproksymacji

polyfit

dopasowanie wielomianu

polyfit(X,Y,N) znajduje współczynniki wielomianu P(X)
stopnia N przybliżającego zbiór danych metodą najmniej-
szych kwadratów.

polyval

wyznaczanie wartości wielomianu

Y=polyval(P,X) , gdzie P jest wektorem współczynników
wielomianu wyznaczonym np. przez funkcję polyfit, jest
wartością wielomianu dla argumentu X.

linspace

wektor wartości liniowo narastających

linspace(x1,x2,N) generuje wektor wierszowy N wartości
równomiernie rozłożonych w przedziale (x1,x2). Jest to
funkcja pomocna w wykreślaniu krzywej aproksymującej
dyskretne wyniki pomiarów, np.:

3.5. Polecenia pomocne w składowaniu wyników

pwd

pokaż aktualny katalog

cd

zmień katalog

dir

wyświetl zawartość aktualnego katalogu

save

zachowaj

Zapis zmiennych z pamięci operacyjnej w pliku dysko-

wym. Dopuszczalne są następujące sposoby użycia in-
strukcji save:

save zapisuje wszystkie zmienne w pliku matlab.mat,
save fname zapisuje wszystkie zmienne w pliku

fname.mat,

save fname X zapisuje tylko zmienną X w pliku

fname. mat w formacie MAT czytanym tylko przez Ma-
tlaba,

save fname X Y Z zapisuje zmienne X, Y, Z w pliku

fname.mat,

save fname X /ascii zapisuje zmienną X w postaci tzw.

liczb ASCII w pliku tekstowym o nazwie fname.
Zamiast znaku "/" można użyć minusa. Pliki zapisane w
kodzie ASCII są rozpoznawalne przez inne programy.

print -dtiff nazwa.tif

zapisz plik gra-

ficzny

Powyższe polecenie zapisuje aktualny rysunek w postaci
pliku graficznego TIFF w aktualnym katalogu (możliwe są
też inne formaty plików graficznych).

print -dwin

drukuj

Powyższe polecenie powoduje wydruk aktualnego rysun-
ku w kolorze czarno-białym.

print -dwinc

drukuj

Powyższe polecenie powoduje wydruk aktualnego rysun-
ku w kolorach.

X=[2 8 14 20]; Y=[3 6 12 15]; %warto

ś

ci

z pomiarów

plot(X,Y,'ro-') %wykres warto

ś

ci rze-

czywistych z pomiaru

wspolcz=polyfit(X,Y,1) %wyznaczenie
współczynników wielomianu 1-go stopnia

Xi=linspace(2,20,100); %wyznaczenie 100
warto

ś

ci, dla których chcemy wyznaczy

ć

warto

ś

ci krzywej aproksymuj

ą

cej

Yi=polyval(wspolcz,Xi); %wyznaczenie
warto

ś

ci wielomianu dla 100 warto

ś

ci Xi

hold on %wykres krzywej aproksymuj

ą

cej

plot(Xi,Yi,'b-') w tym samym układzie
hold off

współrz

ę

dnych

15

P

RZYKŁADOWE PYTANIA KONTROLNE

1.

Dokonaj klasyfikacji błędów pomiarów ze
względu na sposób ich powstawania.

2.

Wyjaśnij pojęcia: błąd bezwzględny pomiaru,
dokładność pomiaru, dokładność przyrządu po-
miarowego.

3.

Omów stosowany w metrologii sposób opisu
błędów przypadkowych.

4.

Scharakteryzuj błędy systematyczne.

5.

Przedstaw reguły przenoszenia błędów w przy-
padku, gdy wielkość mierzona pośrednio jest:

a)

sumą wielkości pomocniczych,

b)

iloczynem wielkości pomocniczych.

Uwzględnij zarówno wzajemną niezależność
błędów pomiarów pośrednich jak i błąd najgor-
szego przypadku. Uzasadnij, że znajomość po-
wyższych reguł jest wystarczająca do wyzna-
czenia błędu w szeregu sytuacjach, w których w
zależności na wielkość Y mierzoną pośrednio
występuje tylko dodawanie (odejmowanie) i
mnożenie (dzielenie) wielkości pomocniczych
X

i

, np.

5

4

3

2

1

X

X

X

X

X

Y

−

+

=

.

6.

Omów pojęcie cyfry znaczącej.

7.

Przedstaw reguły podawania błędu oraz regułę
podawania odpowiedzi.

8.

Omów pojęcia: skala liniowa, skala liniowo-
logarytmiczna, skala logarytmiczno-liniowa,
skala decybelowa.

9.

Wyjaśnij pojęcie aproksymacji.

10.

Omów zagadnienie aproksymacji metodą naj-
mniejszych kwadratów.

11.

Omów podstawowe tryby pracy z pakietem
Matlab.

W

YKAZ LITERATURY

[1]

Chwaleba A., Poniński M., Siedlecki A.: "Me-
trologia

elektryczna",

WNT

Warszawa,

1996,1998, sygn. 53200, 54691.

[2]

Baszun P. i inni: "Miernictwo elektryczne -
ć

wiczenia laboratoryjne", skrypt WAT, War-

szawa, 1988, sygn. S-48721.

[3]

Kwiatkowski W.S.: "Miernictwo elektryczne -
analogowa technika pomiarowa", Oficyna wy-
dawnicza Politechniki Warszawskiej, Warsza-
wa, 1994, sygn. 52120.

[4]

Marcyniuk A. i inni: "Podstawy metrologii
elektrycznej", WNT, Warszawa, 1984.

[5]

Taylor J.R. :"Wstęp do analizy błędu pomiaro-
wego", Wyd. Naukowe PWN, Warszawa, 1995,
1999, sygn. 52951, 55754.