Wybrane przypadki ruchu ciała sztywnego

1.

Prędkość obrotowa koła zamachowego maszyny parowej wynosi u=120 [obr/min]. Po zamknięciu
dopływu pary koło obracając się ruchem jednostajnie opóźnionym wykonało jeszcze u

1

=20 [obr]. Jak

długo obracało się koło po zamknięciu pary?

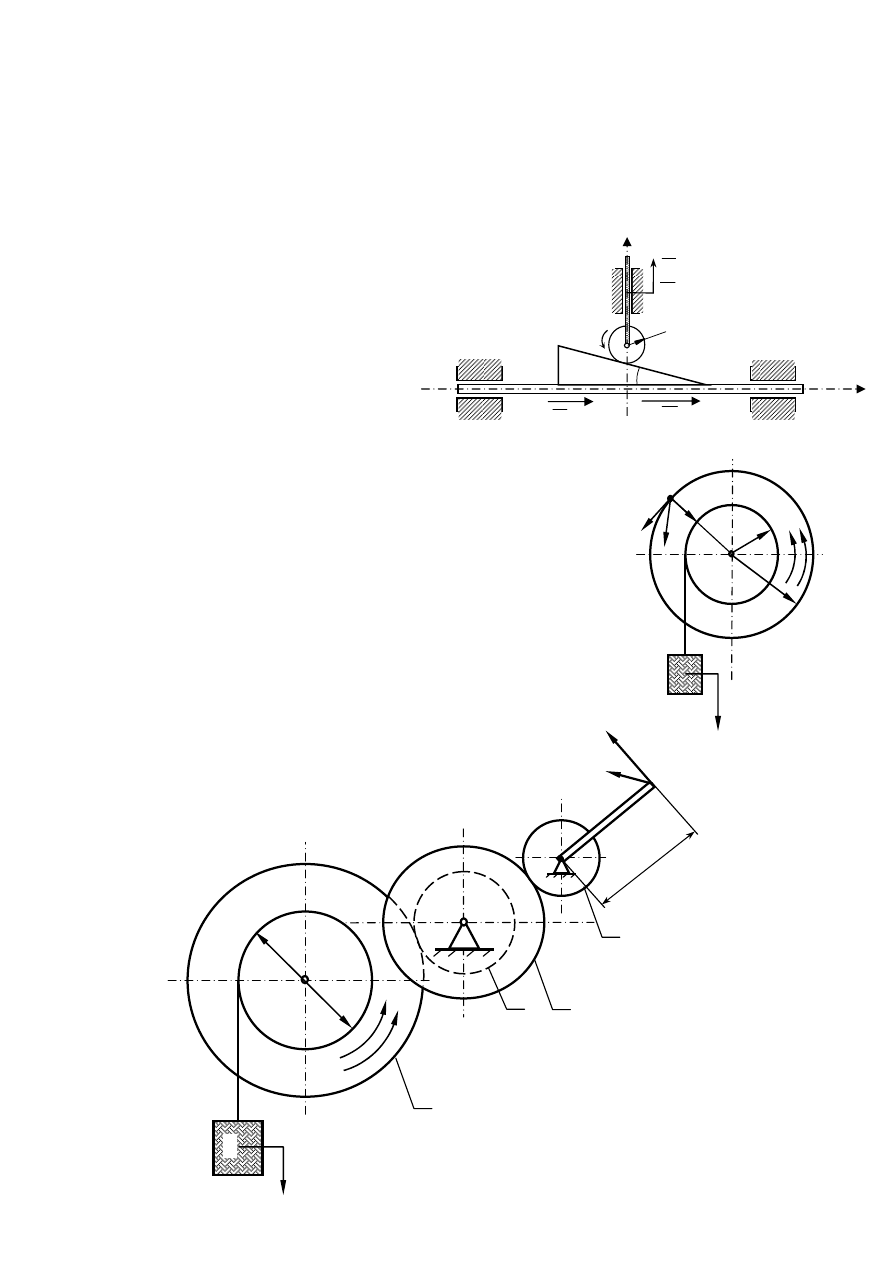
2.

Krzywka AB poruszająca się ruchem
postępowym ma kształt trójkąta, którego
bok kierujący jest nachylony do osi x pod
kątem

α

. Na krzywce poprzez koło O o

promieniu r wsparty jest ślizgający się
swobodnie w łożyskach prostopadły do osi
x sworzeń OC. Wyznaczyć dla chwili t
prędkość (v

s

) i przyspieszenie (a

s

) sworznia

OC, a także prędkość kątową (ω) i
przyspieszenie kątowe (

ε

) koła O, jeżeli

krzywka posuwa się z prędkością v

k

=a

k

⋅

t.

3.

Ciężar (A) podwieszony do linki i nawinięty na bęben kołowrotu
porusza się w dół ruchem postępowym prostoliniowym wg równania:
x=15t

2

, gdzie: x – [cm], t – [s]. Obliczyć: prędkość v

M

(t), oraz

przyspieszenie a

M

(t) punktu M koła korby kołowrotu, jeżeli R=60 [cm],

r=20 [cm].

4.

Ciężar B podnoszony jest kołowrotem z korbą o długości b=400 [mm].
Wskutek uszkodzenia hamulca ciężar zaczął nagle opadać. Równanie
ruchu ciężaru ma postać x=5t

2

, gdzie: x – [cm] ; t – [s]. Średnica bębna

d=200 [mm], liczby zębów mechanizmu kołowrotu wynoszą: z

1

=13,

z

2

=39, z

3

=11, z

4

=77. Obliczyć prędkość (v

A

) i przyspieszenie (a

A

)

końca korby po t=2 [s] od początku ruchu.

B

x

B

v

B

a

B

d

a

A

O

ε

ω

v

A

A

z

1

z

2

z

3

z

4

b

A

x

A

a

A

v

A

R

r

a

a

τ

a

n

O

ε

ω

M

x

y

k

v

k

a

s

a

s

v

α

A

B

O

C

r

ω

,

ε

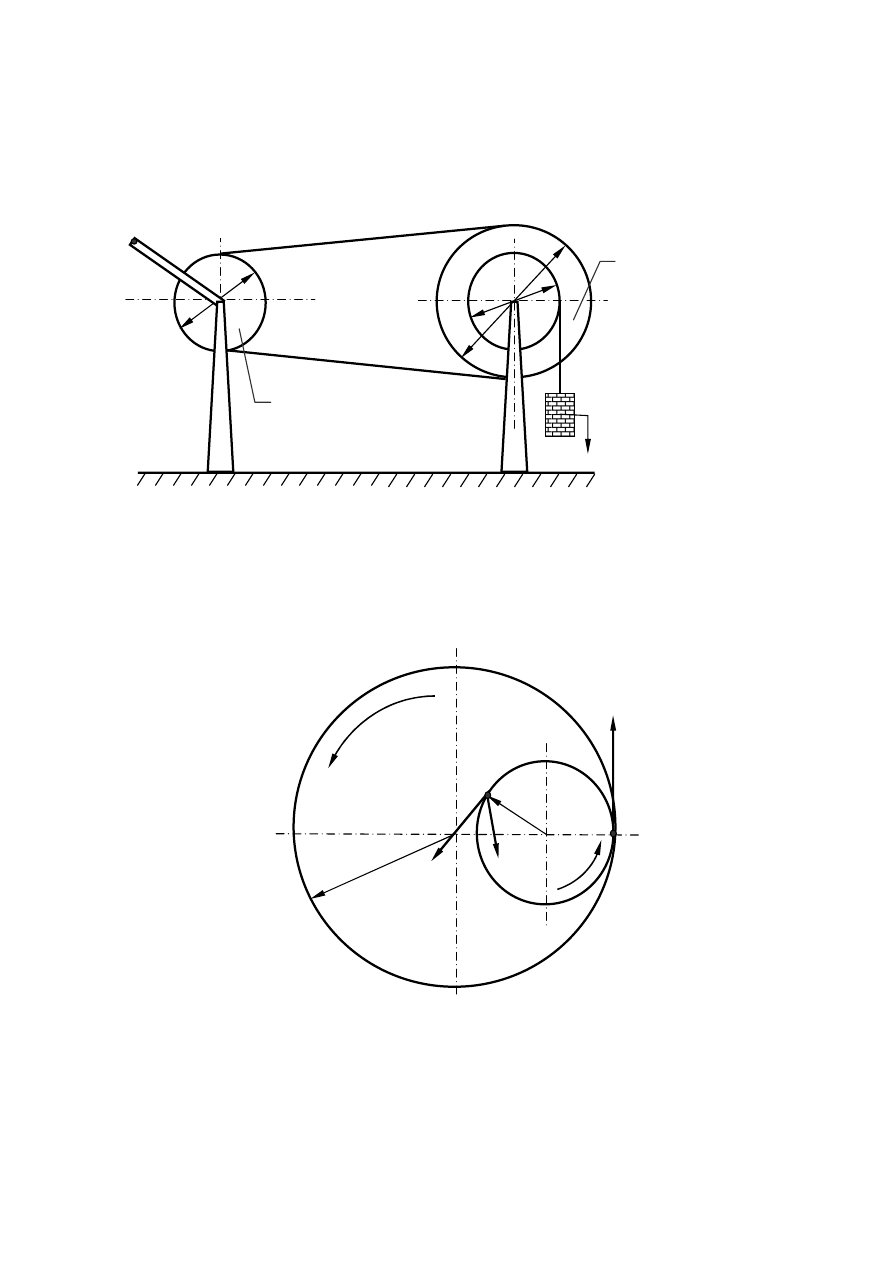
5.

Urządzenie do podnoszenia ciężarów składa się z koła (I) o średnicy (d

1

), które obracane jest korbą o

długości (b) i połączone jest łańcuchem z kołem (II) o średnicy (d

2

). Koło (II) osadzone jest

współosiowo z bębnem o średnicy (d

3

) na który nawinięta jest lina unosząca ciężar (Q). Wskutek

uszkodzenia zapadki ciężar zaczął opadać wg równania x=5t

2

, gdzie x [cm], t [s]. Określić prędkość

(v

A

) i przyspieszenie (a

A

) końca korby (punkt A) po chwili t=3[s].

6.

Koło zębate (I) o ilości zębów z

1

=80 zaczyna się obracać z przyspieszeniem

ε

=

π

[s

-2

] wprawiając w

ruch zazębiające się z nim wewnętrznie koło (II) o liczbie zębów z

2

=20. Obliczyć prędkość kątową

ω

2

koła (II) i przyspieszenie a

B

punktu (B) leżącego na okręgu tego koła po upływie czasu t=1 [s] od

rozpoczęcia ruchu, jeżeli r=15 [cm].

x=5t

2

[cm]

d

1

=10 [cm]

d

2

=40 [cm]

d

3

=20 [cm]

b=30 [cm]

x

φ

d

1

φ

d

2

φ

d

3

II

I

b

A

Q

r

1

O

1

ε

1

I

II

C

v

c

ε

2

r

2

B

v

B

a

B

O

2