dr inż. Mariusz Frukacz
Ć
wiczenia z geodezji II
Transformacja współrzędnych prostokątnych płaskich sposobem Helmerta
Transformacja czteroparametrowa Helmerta wyrażona jest wzorami:
i
i
i
ay
bx
c
X
−
+
=
i
i
i
by
ax
d
Y
+
+
=
(1)
gdzie
x
i
, y
i
– współrzędne i-tego punktu w układzie pierwotnym,
X
i
,
Y
i
- współrzędne i-tego punktu w układzie wtórnym.
Wyznaczenie parametrów transformacji i ocena dokładności
1. Obliczenie wsp. środków ciężkości w obu układach (tylko z punktów dostosowania):
0
[ ]
i
x
x
n
=
;
0
[ ]
i
y
y
n
=
;
0
[
]
i
X
X
n
=
;
0
[ ]
i
Y
Y
n
=
(2)
2. Centrowanie współrz
ę
dnych (obliczenie wsp. zredukowanych o
ś
rodki ci
ęż
ko
ś
ci):
(
)
0
i
i
y
y
y
−
= ∆
,
(
)
0
i
i
x
x
x
−
= ∆
,
(
)
i
0
i
X
X
X
∆
=
−
,
(
)
i
0
i
Y
Y
Y
∆
=
−
(3)
3. Wyznaczenie parametrów transformacji:
(
)
(
)
∑
∑
=
=
∆
+
∆
∆
∆
−
∆
∆
=
n
1
i
2
i
2
i
n
1
i
i
i
i
i
y
x
X
y
Y
x
a
;
(
)
(
)
∑
∑
=
=
∆
+
∆
∆
∆
+
∆
∆
=
n
1
i
2
i
2
i
n
1
i
i
i
i
i
y
x
Y
y
X
x
b
(4)
0
0
0
c
y a
x b
X
=
−
+
;
0
0
0
d
x a
y b Y
= −
−
+
(5)
Je
ś
li (5) podstawimy do (1) to otrzymamy drug
ą
wersj
ę
wzorów na transformacj
ę
:
(
) (
)
0
0
0
i
i
i
X
X
x
x b
y
y
a
=
+
−
−
−
(
) (
)
0
0
0
i
i
i
Y
Y
x
x a
y
y b
= +
−
+
−
(6)
4. Obliczenie poprawek dla punktów dostosowania:
i
t
X
i
i
V
X
X
=
−
;
i
t
Y
i
i
V
Y
Y
= −
(7)
5. Ocena dokładno
ś
ci
2
2
0
0
2
2
4
i
i
V
V
m
m
n u
n
=
⇒
=
−
−
∑
∑
(8)
Jako kryterium oceny dokładno
ś
ci transformacji, w formie zgeneralizowanej, mo
ż
emy poda
ć
warunek
.
dop
p
0
m
2
1
m
≤
, gdzie
.
dop
p
m
jest dopuszczalnym
ś
rednim bł
ę
dem poło
ż
enia punktu w
okre
ś
lonej klasie osnowy.
dr inż. Mariusz Frukacz
Ć
wiczenia z geodezji II
6. Obliczenie korekt post-transformacyjnych Hausbrandta:
(
)
∑
∑
=
=
=
n
1
i
ji
n
1
i
i
X
ji
j
X
r
V
r
V
;
(
)
∑
∑
=
=
=
n
1
i
ji
n
1
i
i
Y
ji
j
Y
r
V
r
V
(9)
gdzie
2
j
i
2
j
i
2
ji
ji
)
Y
Y
(
)
X
X
(
1
d
1
r
−
+
−
=
=
(10)
r
ji
– waga (i = 1, 2, ... , n),
n – liczba punktów dostosowania.
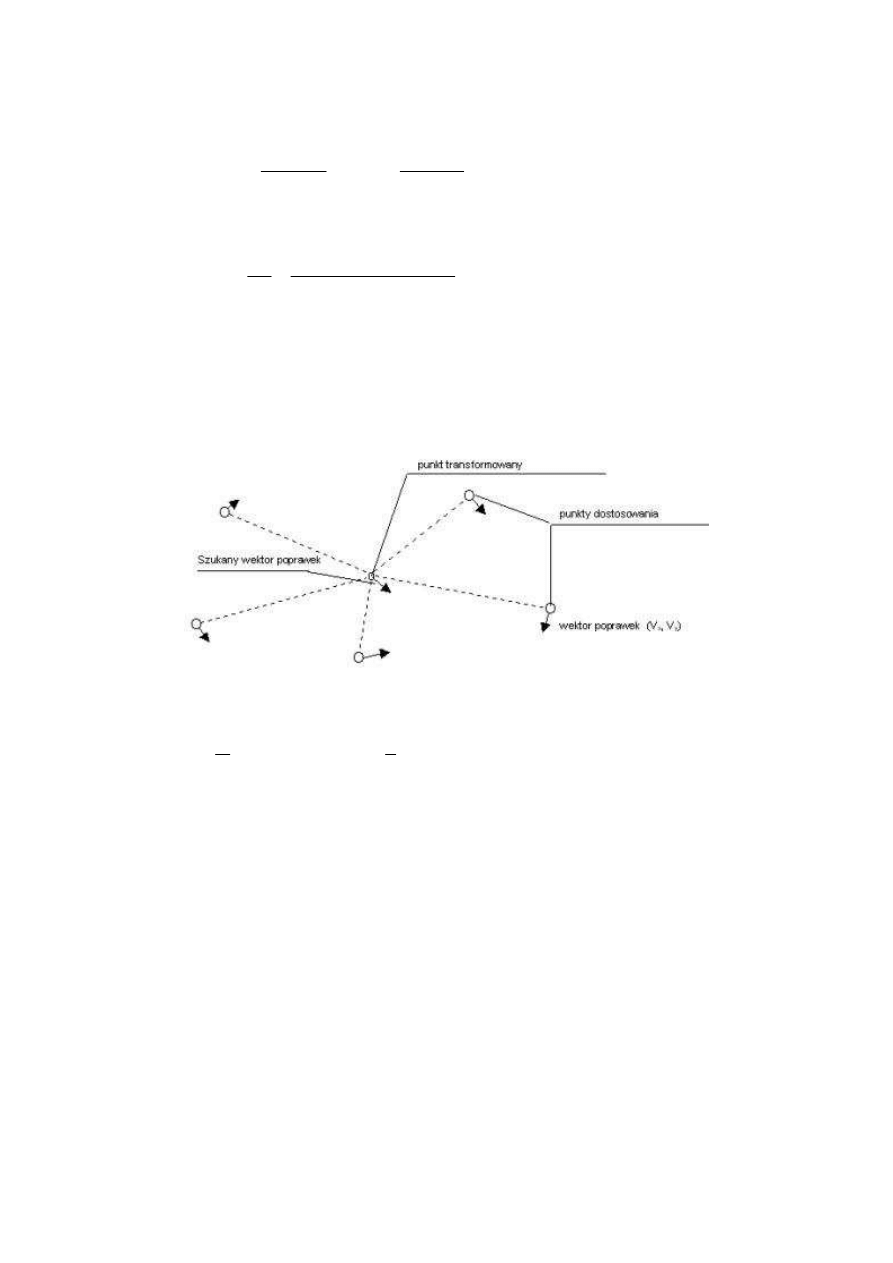
Elementy przyj
ę
te do liczenia wag i ich oznaczenia zastosowane we wzorach (9) i (10) zilustrowano
na rysunku.
7. Obliczenie ostatecznych warto
ś
ci współrz
ę
dnych:
j
j
j
X
X
X
V
=
+
;
j
j
j
Y
Y
Y
V
= +
(11)
Wyznaczenie parametrów transformacji z zapisu macierzowego układu równań poprawek
1. Uło
ż
enie równa
ń
poprawek (wprowadzaj
ą
c (1) do (7)):
1
1
1
X
i
V
y a
x b c
X
=
−
− +
1
1
1
Y
i
V
x a
y b d
Y
= −
−
− +
........................................
(12)
n
X
n
n
n
V
y a
x b c
X
=
−
− +
n
Y
n
n
n
V
x a
y b d
Y
= −
−
− +
2. Zapis macierzowy wzorów (12) ma nast
ę
puj
ą
c
ą
posta
ć
:
L
AX
V
+
=
(13)
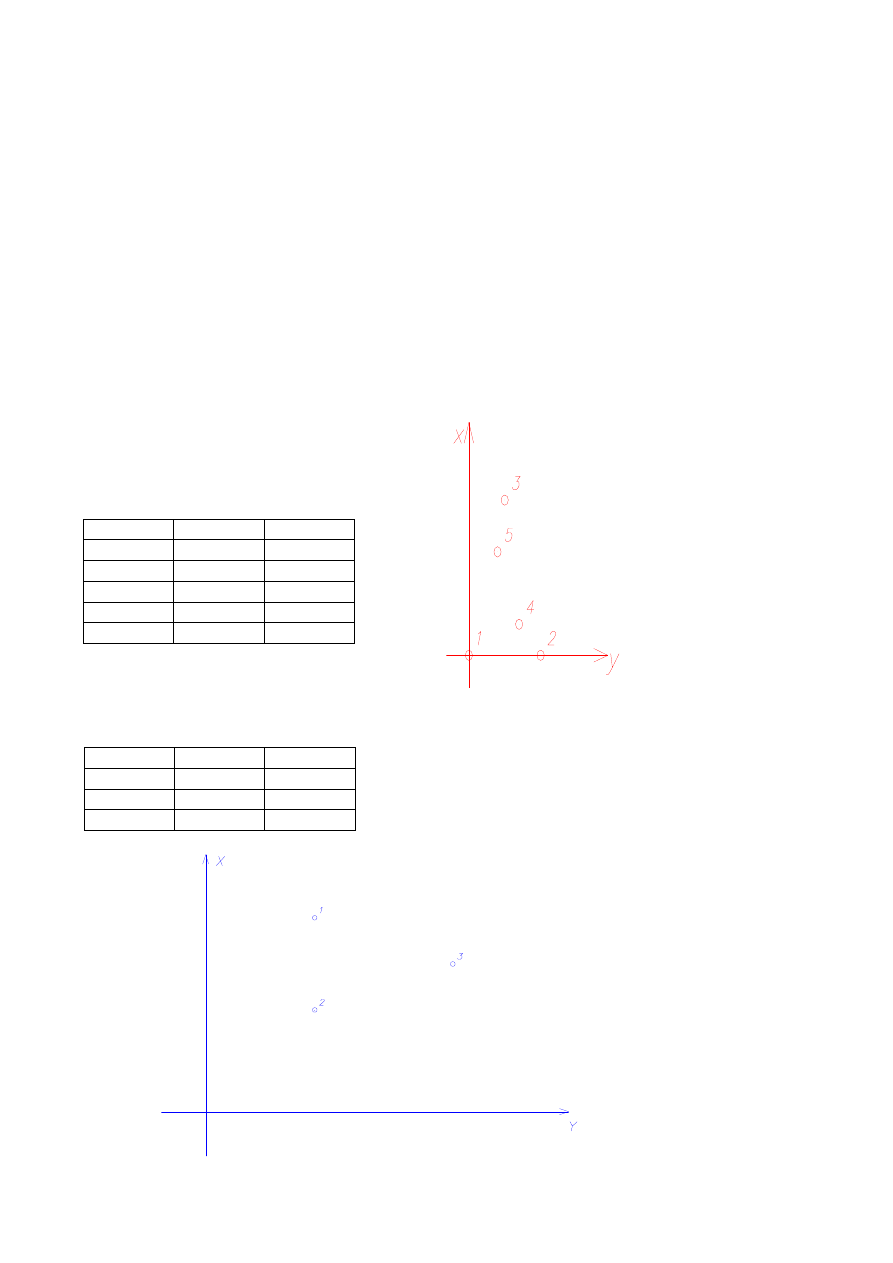
dr inż. Mariusz Frukacz
Ć
wiczenia z geodezji II
gdzie
V
V
V
V
V
n
Y
n
X
1
Y
1
X
=
⋮
1
1
1
1
1 0
0
1
...................
...................
1 0
0
1
n
n
n
n
y
x
x
y
A
y
x
x
y
− −
−
−
−
=
− −
−
−
−
X
d
c
b
a
=
L
Y
X
Y
X
n
n
1
1
=
⋮
(14)
3. Stosuj
ą
c warunek
min
V
V
T
=
=
Φ
obliczamy wektor parametrów
( )
L
A
A
A
X
T
1
T
−
−
=
(15)
Punkty 4 –7 bez zmian.
Przykład:
Układ pierwotny:
Nr
X
Y
1
0.000
0.000
2
0.000
10.000
3
15.000
5.000
4
3.000
7.000
5
10.000
4.000
Układ wtórny:
Nr
X
Y
1
120.006
99.987
2
100.015
100.008
3
109.985
130.003